扰动观测器在惯导平台稳定回路中的应用方法

王琛琛, 王新龙, 黄 海



扰动观测器在惯导平台稳定回路中的应用方法

王琛琛1, 王新龙1, 黄 海2

(1. 北京航空航天大学 宇航学院, 北京, 100191; 2. 中国船舶重工集团公司第705研究所, 陕西 西安, 710075)

惯性技术的发展对惯导平台稳定回路稳定性、抗干扰性等性能的要求越来越高, 但摩擦力矩以及其他各种干扰力矩对稳定回路性能的进一步提高产生了严重影响。为了有效克服这些干扰力矩对稳定回路性能的影响, 在传统比例微分积分(PID)方法对稳定回路进行控制的基础上, 提出了一种利用扰动观测器来抑制干扰力矩以提高稳定回路性能的方法。通过利用回路中力矩电流和角速度信息构成扰动观测器, 对作用于平台系统的干扰力矩进行抑制。仿真结果表明, 扰动观测器的引入没有影响原有PID控制稳定回路的动态性能, 且能够对干扰进行有效的抑制, 提高了稳定回路的稳定精度和抗干扰性。

扰动观测器; 传统比例微分积分控制; 惯性平台; 稳定回路

0 引言

目前, 平台式惯导系统凭借其自主性强的特点, 在水下潜器、水面舰船等潜载武器系统中得到了广泛的应用。

稳定回路作为平台式惯导的关键环节, 回路的稳定性、快速性及抗干扰性等因素直接影响着惯导系统的导航性能。目前, 稳定回路应用较多的是传统比例积分微分(proportion-integration- differentiation, PID)控制, 虽然该方法实现起来简单, 但基于此方法的稳定回路稳定精度不高、抗干扰性不强。国内外学者对此进行了大量的研究, 提出的方法主要有: 变结构控制[1]、模糊PID控制[2]、自抗扰控制[3]、低速自适应PID控制[4]、基于神经网络的PID控制[5]及∞鲁棒控制[6]等。和传统的PID控制相比, 这些方法在系统稳定性、抗干扰性虽都有所改进, 但是实现起来比较复杂。

基于此, 本文在利用传统PID方法对稳定回路控制的基础上, 设计了一种基于扰动观测器抑制扰动的方法。该方法可以实时预测系统的干扰并对其补偿, 减小了各种干扰及参数变化对系统稳定精度的影响, 且结构简单、计算量小。

1 惯导平台稳定回路的组成

1.1 惯导平台稳定回路的组成

通常, 稳定回路由机械平台、三环框架、安装在平台上的陀螺仪、力矩电机、坐标变换器和控制电路组成, 如图1所示。图中:M为总的干扰力矩;M为力矩电机产生的力矩。

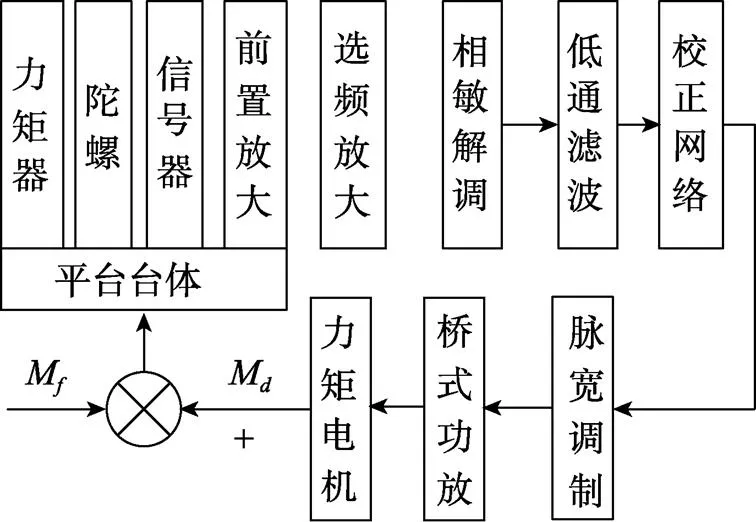
图1 稳定回路结构原理框图

机械平台是安装陀螺仪和加速度计的载体, 三环框架为其提供3个方向的转动自由度。陀螺仪是角速度敏感元件, 当有干扰力矩M作用在台体框架轴上时, 它会敏感该轴的转动角速度, 输出幅度与此角速度成比例的正弦信号。该正弦信号经前置放大环节, 传输给控制电路板, 在控制电路板上进行选频放大、带通滤波、全波相敏解调、低通滤波、校正、直流放大及脉冲宽度调制(pulse width modulation, PWM), 再经桥式功率放大后驱动力矩电机, 产生力矩M, 以抵消作用在台体框架上的干扰力矩。其中, 三环框架有3条稳定回路: 方位回路、俯仰回路和横滚回路。这3条回路之间存在着交叉耦合作用, 一般情况下, 可将这种耦合作用当成外界扰动, 按单通道设计稳定回路[7]。由于3条回路的工作原理基本相同, 因此, 本文以方位通道为例对稳定回路进行设计分析。

1.2 稳定回路的控制结构

对于平台式惯导的稳定回路, 一般来说, 除了校正网络、直流力矩电机和陀螺仪外, 其他环节都可看成比例环节[8], 采用“电流环、速度环、位置环”控制, 其控制框图如图2所示。

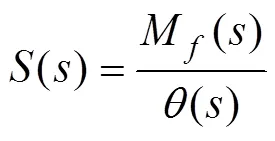
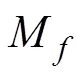
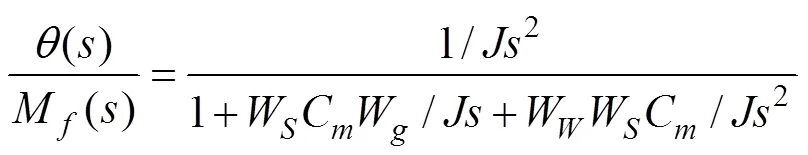
即稳定回路的力矩刚度为

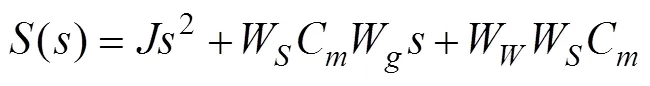
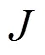
2 基于扰动观测器的回路控制

2.1 扰动观测器的设计

作用于稳定平台系统的摩擦力矩、结构质心静不平衡力矩、风阻力矩以及其他干扰力矩存在着非线性和不确定性, 难以通过对扰动建立精确的模型进行补偿。因此本文采用一种非模型的补偿方式—扰动观测器的方法对扰动进行补偿。

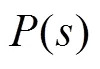
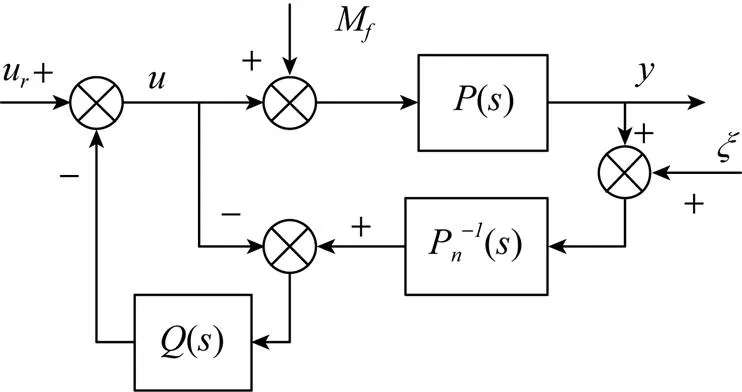
图3 扰动观测器的基本结构

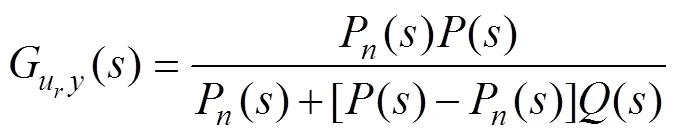
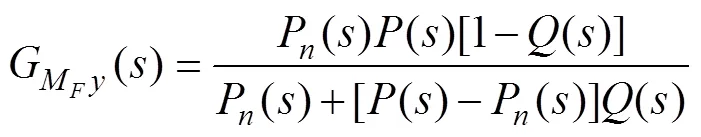
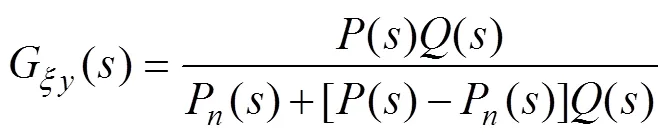
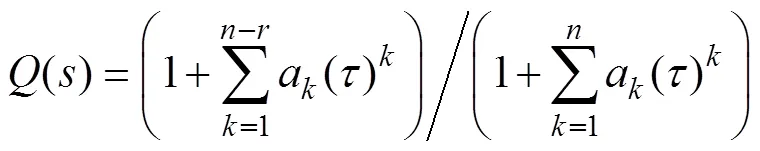
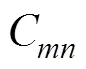
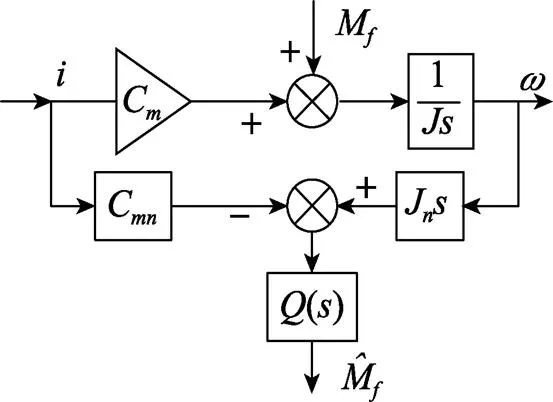
图4 扰动观测器的结构图

由图4可得

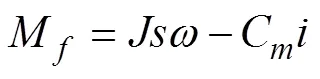
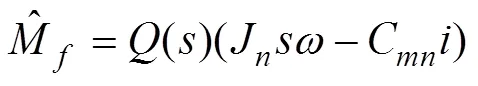
根据式(7)将扰动观测器设计为

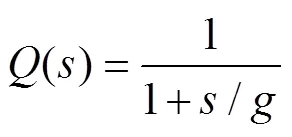
则有

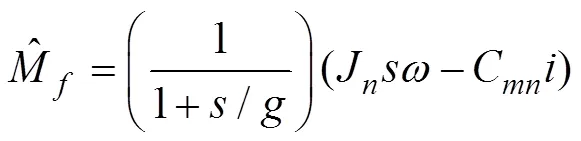
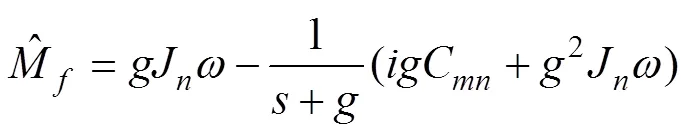
由此, 可得改进后的扰动观测器如图5所示。

2.2 扰动观测器在稳定回路中的实现

当有扰动力矩作用在台体轴时, 力矩电机会有电流产生, 陀螺仪会有角速度输出, 产生的电流和陀螺仪敏感到的角速度送入扰动观测器中, 扰动观测器将估计出来的力矩经电机力矩系数的逆变换前馈到稳定回路中, 回路中力矩电机产生与干扰力矩大小相当、方向相反的抵抗力矩, 从而实现了对干扰的有效抑制。

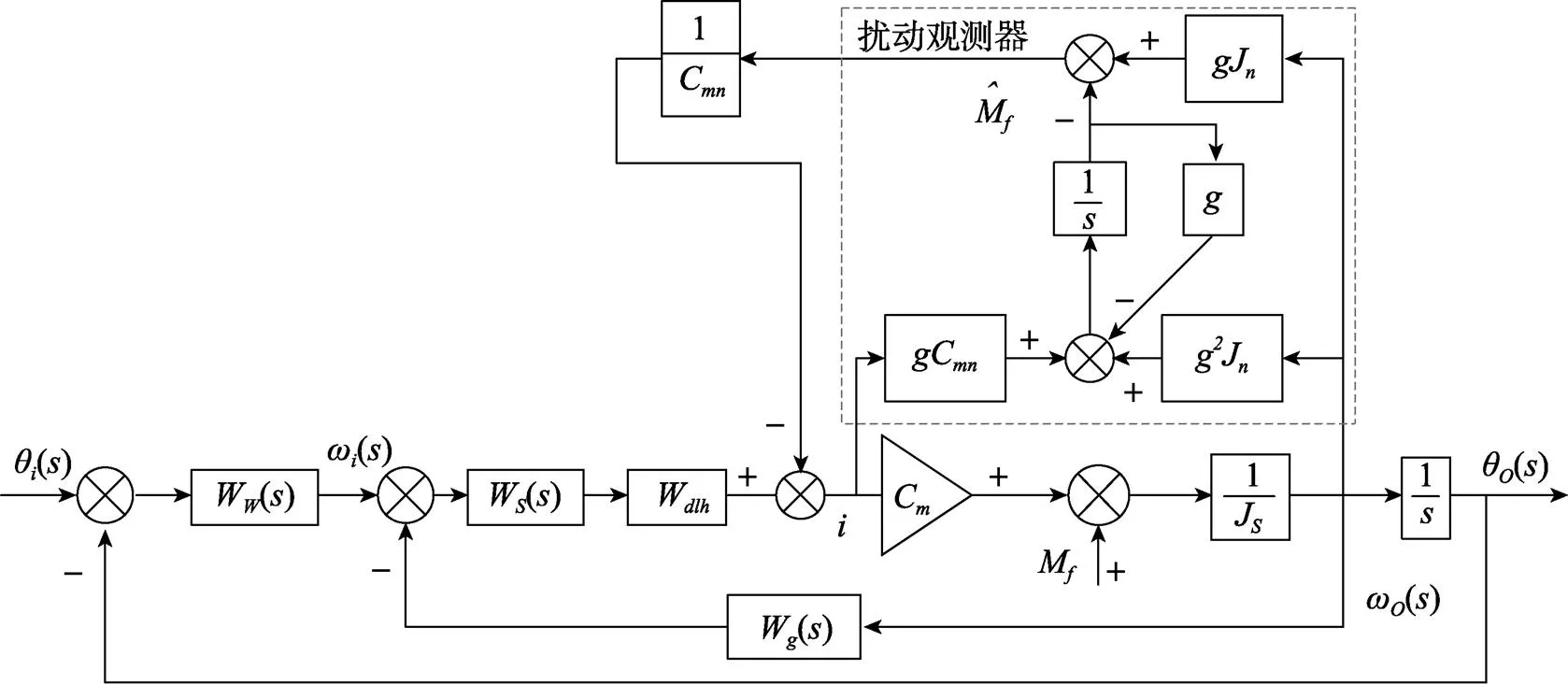
图6 带有扰动观器的稳定回路控制结构图

3 仿真验证与分析

根据稳定回路的设计指标利用MATLAB/ Simulink软件先后将电流环、速度环、位置环控制器设计成如下形式

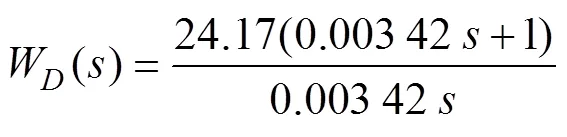
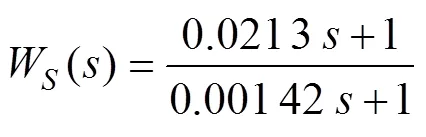
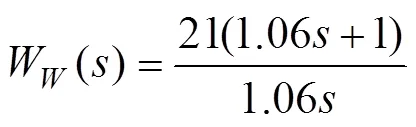
为了分析扰动观测器的引入对平台稳定回路动态过程的影响, 对引入扰动观测器前后的稳定回路分别进行了仿真, 仿真结果如图7、图8所示。

从图7、图8可看出, 扰动观测器引入前后, 系统的带宽均约为21 Hz, 稳定回路的频率响应曲线几乎相同, 可见扰动观测器的加入没有影响系统的动态响应过程。

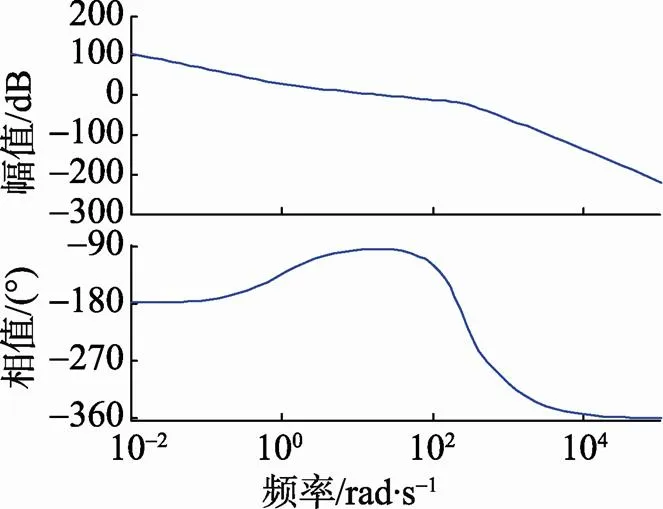
图7 未引入扰动观测器系统频率响应特性

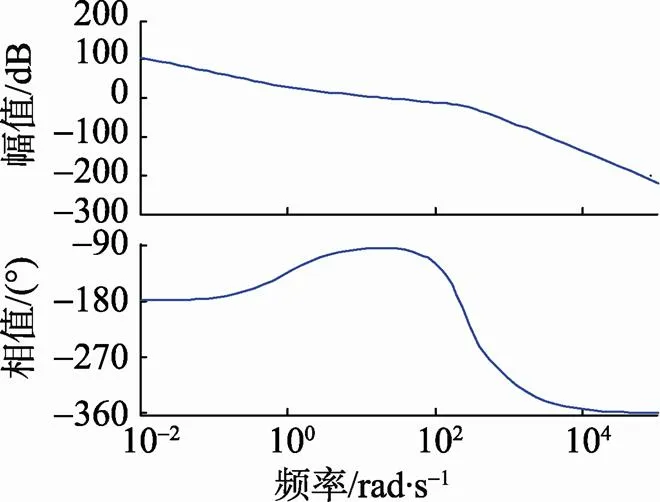
图8 引入扰动观测器系统频率响应特性

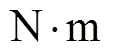
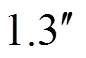
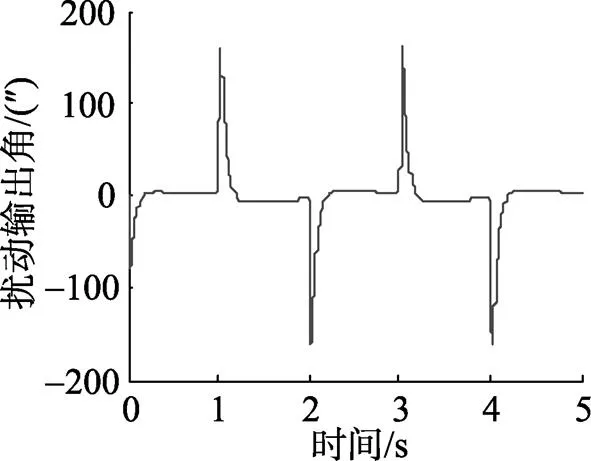
图9 方波干扰下未引入观测器系统输出角

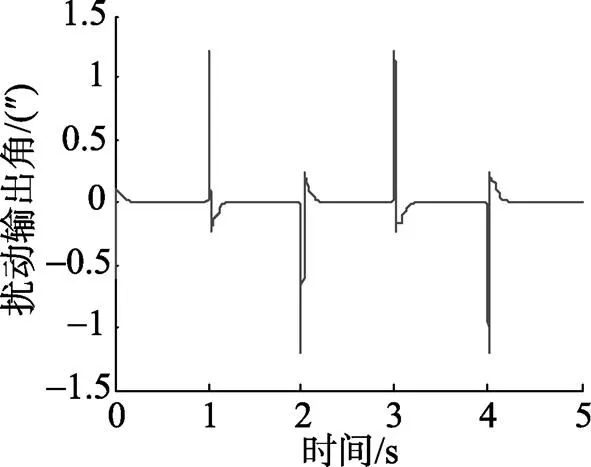
图10 方波干扰下引入观测器系统输出角

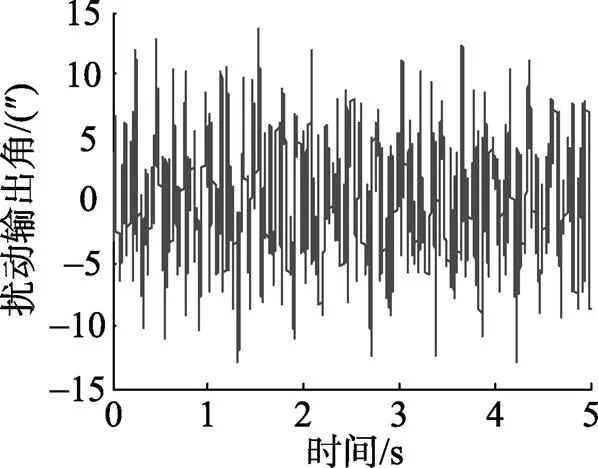
图11 随机干扰下未引入观测器系统输出角

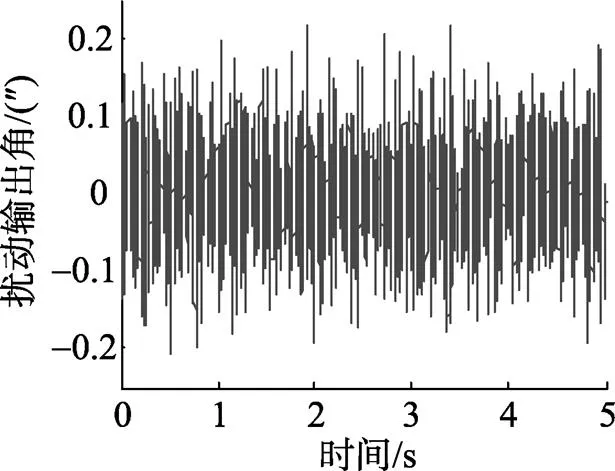
图12 随机干扰下引入观测器系统输出角

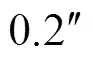
仿真结果表明, 无论是对于摩擦力矩、平台框架静不平衡力矩等具有周期特性的干扰力矩, 还是对风阻力矩等具有随机特性的干扰力矩, 扰动观测器的引入均能对干扰进行抑制, 从而有效提高了平台式惯导系统稳定回路的抗干扰性和精确性。

4 结论

针对传统PID控制的稳定回路抗扰性不强,稳定精度不高的问题, 本文提出了一种在传统PID的基础上引用扰动观测器对稳定回路扰动进行补偿的方法, 进一步通过仿真验证, 可以得到如下结论。

1) 利用扰动观测器对惯导平台稳定回路的干扰进行补偿, 不需要对干扰信号进行精确建模, 干扰信号可通过力矩电流和角速度间接的将扰动估计出来, 且观测器结构简单, 便于实现。

2) 扰动观测器引入前后稳定回路的带宽基本不变, 引入观测器没有影响原有稳定回路的动态响应过程。

3) 扰动观测器能有效的抑制作用于平台系统的干扰力矩, 并且当干扰力矩具有周期特性时抑制效果更加明显。

由此可见, 将扰动观测器应用在传统PID控制的稳定回路中是一种提高稳定回路性能的简单、有效的方法。

[1] 伍小芹, 黄德鸣. 平台稳定回路的变结构控制[J]. 海南大学学报自然科学版, 2001, 19(2): 132-135. Wu Xiao-qin, Huang De-ming. The Sliding Variable Control in the Inertial Platform Servo Loop[J]. Natural Science Journal of Hainan University, 2001, 19(2): 132-135.

[2] 张建灵, 刘小刚, 安锦文, 等. 模糊PID控制在制导滑翔弾滚动稳定回路中的应用[J]. 火力与指挥控制, 2005, 30(3): 44-46. Zhang Jian-ling, Liu Xiao-gang，An Jin-wen. Application of the Fuzzy-PID Control to the Roll Stabilized Loop of the Homing Gliding Missile[J]. Fire Control and Command Control, 2005, 30(3): 44-46.

[3] Zhang Qing, Tan Zhen-fan, Liang Ying. Gyro Stabilized System Based on Auto-disturbance Rejection Controller[C]//2008 ISECS International Colloquium on Computing, Communication, Control, and Management, 2008: 34-38.

[4] 张苗欢, 赵琳, 罗霞. 惯性平台稳定回路的单神经元自适应PID控制[J]. 哈尔滨工程大学学报(增刊), 2006, 27(Z): 88-91. Zhang Miao-huan, Zhao Lin, Luo Xia. Single Neuron Adaptive PID Control of the Stabilizing Circuits for Inertia Platform[J]. Journal of Harbin Engineering University, 2006, 27(Z): 88-91.

[5] 徐立新, 张宇河, 王长虹, 等. 用神经网络实现精密伺服系统中扰动力矩的动态补偿[J]. 自动化学报, 1998, 24(1): 108-112. Xu Li-xin, Zhang Yu-he，Wang Chang-hong, et al. The Disturbance Torque Dynamic Compensation Using Neutral Network in Ultra-accuracy Servo System[J]. Acta Automatica Sinica, 1998, 24(1): 108-112.

[6] 魏宗康, 徐强, 夏刚, 等. 平台稳定回路∞鲁棒控制设计[J]. 中国惯性技术学报, 2001, 9(3): 1-8. Wei Zong-kang, Xu Qiang, Xia Gang, et al. Design of∞Robust Control for Platform’s Servo Loop[J]. Journal of Chinese Inertial Technology, 2001, 9(3): 1-8.

[7] Zdeněk Hurák, Martin Řezáč. Image—Based Pointing and Tracking for Inertially Stabilized Airborne Camera Platform[J]. IEEE Transaction on Control Systems Technology, 2011(99): 1-14.

[8] 孙宁, 刘洁瑜, 周小刚, 等. 光纤陀螺惯性平台数字稳定回路设计[J]. 电光与控制, 2007, 14(3):131-135. Sun Ning, Liu Jie-yu, Zhou Xiao-gang, et al. Design of a Digital Position Stabilization Loop for FOG Inertial Platform[J]. Electronics Optics & Control, 2007, 14(3): 131-135.

[9] Bong Keun Kim, Wan Kyun Chung. Advanced Disturbance Observer Design for Mechanical Positioning Systems[J]. IEEE Transactions on Industrial Electronics, 2003, 50(6): 1207-1216.

[10] Makoto Iwasaki, Nobuyuki Matsui. Robust Speed Control of IM with Torque Feedforward Control[J]. IEEE Transactions on Industrial Electronics, 1993, 40(6): 627- 632.

[11] Koji, Satoshi, Muneski, et al. Analysis and Classical Control Design of Servo System Using High Order Disturbance Observer[C]//Processing 1997 IEEE International Conference on Industrial Electronics, Control, and Instrumentation, 1997, 49: 4-9.

Application of Disturbance Observer to Stabilization Loop in Inertial Platform

WANG Chen-chen, WANG Xin-long, Huang Hai

(1. School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China; 2. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

Torques of friction and other disturbance counteract the performance improvement of the stabilization loop in inertial stable platform. To overcome these torques, a method utilizing disturbance observer to inhibit the disturbance torques is proposed on the basis of the traditional proportion-integration-differentiation (PID) control method. The disturbance observer is composed of the torque current and angular velocity. Simulationresults show that introduction of the disturbance observer effectively inhibits the disturbance torqueswithout influencing the dynamic performance of the original PID controlled stabilization loop and, hence enhances the accuracy and disturbance-inhibition capability of the stabilization loop.

disturbance observer; traditional proportion-integration-differentiation (PID) control; inertial platform; stabiliza- tion loop

TJ765.3

A

1673-1948(2012)03-0195-06

2011-11-11;

2012-02-16.

王琛琛(1987-), 女, 在读硕士, 研究方向为导航制导与控制技术.

(责任编辑: 杨力军)