气动不平衡式发射装置气水回收过程仿真与分析
练永庆, 周厚成, 吴开锋, 田 兵
气动不平衡式发射装置气水回收过程仿真与分析
练永庆1, 周厚成2, 吴开锋3, 田 兵1
(1.海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 中国人民解放军国防大学, 北京, 100091;3. 中国人民解放军91341部队, 山东 威海, 264200)
当潜艇使用气动不平衡式发射装置发射鱼雷时, 无泡系统的气水回收过程对潜艇的隐蔽性与艇体均衡均有直接影响。为了对无泡系统气水回收过程进行研究, 建立了无泡系统的定时调节器、无泡气瓶、泄放阀等各组成部件的数学模型, 并结合已有的气动不平衡发射系统的数学模型, 进行了无泡系统气水回收过程的仿真。仿真结果与实际回收海水量的结果对比表明, 所建立的模型基本正确, 可用于气动不平衡式发射装置无泡系统的分析与论证。
鱼雷; 潜艇; 气动不平衡式发射装置; 无泡系统; 仿真
0 引言
气动不平衡式发射装置是潜艇主要的鱼雷发射装置之一[1]。该装置主要由发射管及其管上机械、空气发射系统(发射阀、发射气瓶等)、无泡系统等组成(见图1)。由于该装置具有结构简单、体积小、重量轻和造价低的优点, 在许多中、小型潜艇平台中仍具有较大的应用前景。以往对该装置的研究多集中在其空气发射系统与鱼雷内弹道方面[2-3], 而与潜艇发射过程中的隐蔽性与艇体均衡密切相关的无泡系统气水回收过程研究甚少, 为此本文以俄罗斯ГС-45型潜艇鱼雷发射装置为例, 通过对其无泡系统进行建模与仿真, 对该系统的气水回收过程进行分析。
1 气动不平衡式发射装置无泡系统组成及工作原理
1.1 无泡系统基本组成
气动不平衡式发射装置的气水回收过程与其无泡系统密切相关。无泡系统主要由无泡气瓶、定时调节器和泄放阀等组成(见图1)。其中, 无泡气瓶为泄放阀的打开提供动力, 而定时调节器则可根据不同发射深度控制泄放阀打开的时间, 是无泡系统的核心。定时调节器分两部分(见图2), 分别为送气部分和放气部分, 其中送气部分控制泄放阀开启的时机、放气部分控制泄放阀打开的持续时间。

图1 气动不平衡式发射装置原理图
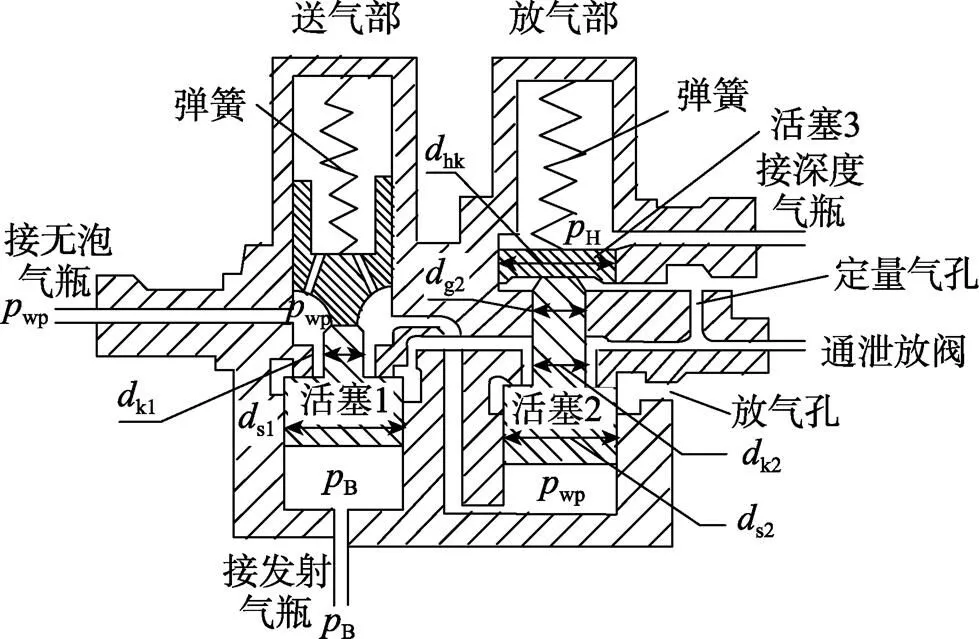
图2 定时调节器原理图
1.2 无泡系统工作原理
气动不平衡式发射装置发射时, 发射气瓶中的高压空气经过发射阀, 单向阀进入发射管推动鱼雷运动, 当发射气瓶压力降到一定程度时(鱼雷约有四分之三离开发射管), 定时调节器的送气部分动作, 无泡气瓶的气体进入泄放阀, 当无泡气瓶的高压空气推压泄放阀活塞向下的力, 大于其弹簧力及发射管内作用于泄放阀阀盘上之空气压力的合力时, 打开泄放阀, 将发射管中的废气和海水回收到艇上的无泡水柜中。在定时调节器送气部开启时, 无泡气瓶的空气通过定量气孔排到大气中, 无泡气瓶压力逐渐下降, 当无泡气瓶压力降到一定程度, 其作用在活塞2的力小于放气部弹簧弹力以及所用在活塞3上的海水压力之和, 活塞2处的密封面打开, 无泡气瓶及泄放阀处的高压空气迅速从放气孔放出, 泄放阀关闭, 气水回收过程结束。
为了便于对气水回收过程进行建模与仿真, 对该过程进行了简化, 即无泡系统回收气水的过程中, 泄放阀打开时首先回收发射管内的空气, 发射管内空气压力小于外部海水压力时, 海水经过发射管与鱼雷之间的间隙进入发射管。当海水填满发射管时, 才开始回收海水, 直至泄放阀关闭。
2 无泡系统数学模型
2.1 定时调节器模型
1) 定时调节器送气部分动作时发射气瓶压力计算
当发射气瓶压力降到一定程度时, 送气部分的无泡气瓶压力、弹簧力以及发射气瓶压力之间形成的力平衡被打破, 定时调节器活塞1向下运动, 无泡气瓶的高压气可经过活塞1的密封面达到泄放阀活塞。
定时调节器送气部分动作的条件为

由上式可求出送气部分动作时, 发射气瓶的压力

2) 定时调节器放气部分定量气孔放气模型
当泄放阀打开时, 无泡气瓶中的空气经定量气孔放到舱室中。假设气体的流动过程是等熵的, 根据空气动力学理论[4], 无泡气瓶空气经定量气孔流到舱室的流量为
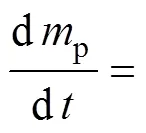
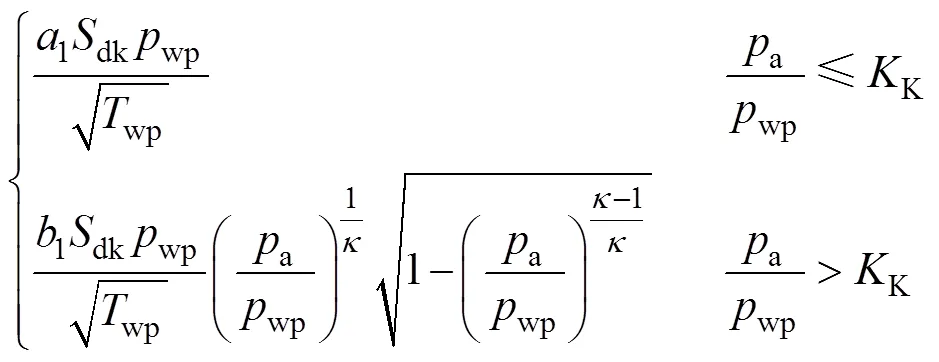
3) 定时调节器放气部分动作模型
定时调节器的送气部分动作取决于无泡气瓶的压力降。送气部分动作时无泡气瓶压力可通过下式计算


2.2 无泡气瓶模型
该模型用于描述无泡系统工作过程中无泡气瓶中气体的压力、温度以及质量的变化。
假设无泡气瓶的放气过程为绝热过程, 则由气体热力学定律经推导, 有


若忽略气体的泄漏, 根据质量守恒定律, 有

2.3 泄放阀数学模型
1) 泄放阀打开时的压强
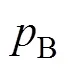

式中: 为泄放阀工作面积; 为阀杆的面积; 为泄放阀活塞面积; 为导向杆的面积; 为泄放阀弹簧的压紧力。
2) 泄放阀的开启面积
泄放阀的理论打开面积为阀门的平衡开度与阀门周长的乘积, 平衡开度可由其弹簧受力后的平衡位置来确定, 即

因此, 泄放阀理论打开面积

水工隧洞混凝土质量通病主要表现为以下几项:蜂窝麻面、水泡、气泡、错台、裂缝、颜色不均、结合部位烂根、冷缝等质量通病。
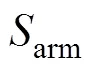

3) 通过泄放阀的回收空气量计算
泄放阀首先回收发射管内空气, 空气经泄放阀流进无泡水柜的空气流量的计算模型同式(3)
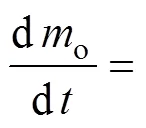

4) 通过泄放阀的回收海水量计算
为了在仿真中计算海水回收量, 须在数学模型中做以下工作。


2.4 无泡水柜内气体状态方程
该无泡水柜控制体的方程如下


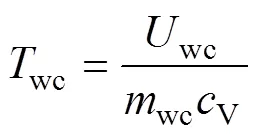



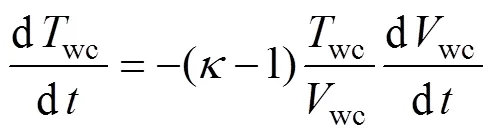
3 气水回收过程的仿真与分析
根据以上建立的无泡系统数学模型, 结合已有的气动不平衡发射系统数学模型[2], 以4阶龙格–库塔算法作为求解微分方程的基本算法, 编制仿真程序。在给定初始条件下, 运用仿真程序即可对发射过程进行仿真。
3.1 仿真结果
通过仿真可获得不同发射深度条件下回收气水的结果。这里给出发射深度分别为45 m, 35 m, 25 m, 15 m时的结果, 如表1所示。发射后期泄放阀回收空气与海水过程曲线分别见图4和图5。

表1 无泡系统仿真结果

图4 泄放阀回收空气量随时间变化图
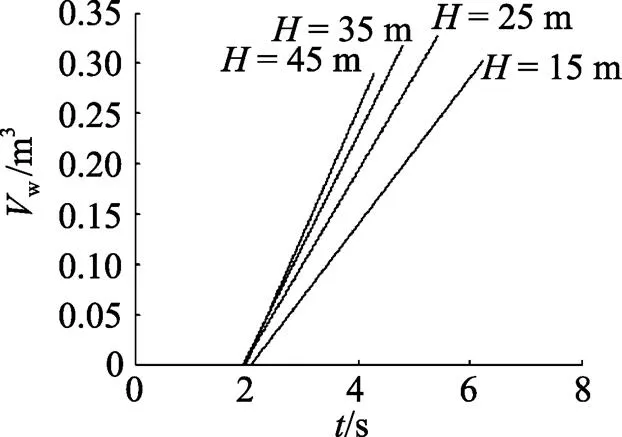
图5 泄放阀回收海水量时间变化图
3.2 仿真结果分析
通过对仿真结果进行分析, 可以得出:
1) 泄放阀开启时刻与发射深度相关, 发射深度越大, 开启时刻推迟(见表1)。这是因为虽然定时调节器送气部分动作不受外部海水压力影响, 但泄放阀的开启还与发射管内压力有关, 即与外部海水压力有关, 发射深度大, 外部海水压力大, 泄放阀开启推迟。
2) 泄放阀开启延时时间受发射深度影响较大, 发射深度越大, 泄放阀开启延时时间越短(见表1)。这是因为定时调节器放气部分动作受海水压力控制, 发射深度大, 海水压力大, 放气部分动作早, 因此泄放阀关闭早。
3) 泄放阀回收空气量与发射过程中注入发射管的气量是相同的, 发射深度大, 所需气量大, 回收气量相应增大(见图4)。
4) 在不同发射深度泄放阀回收海水量基本相同, 约为300 L左右。这与ГС-45发射装置要求回收水量为150~400 L的技术指标相符。在泄放阀开启面积固定的条件下, 海水的回收取决于外部海水压力与泄放阀开启延时时间。发射深度大时, 海水回收速度快(见图5), 为保证不同深度具有相同的回收海水量, 只能通过减小泄放阀开启时间(见表1)来实现。从仿真结果来看, ГС-45定时调节器的结构设计基本实现了发射装置对回收水量的要求。
4 结束语
通过建立无泡系统的数学模型, 并结合已有的气动不平衡发射系统数学模型, 对无泡系统气水回收过程进行了仿真。仿真结果表明, 所建立的模型基本能反映发射后期气水回收过程的基本规律。所建立数学模型可用于该类发射装置无泡系统论证与设计过程的理论分析与研究。
[1] 王树宗, 王一中. 海军舰艇武器装备概论[M]. 北京: 兵器工业出版社, 1995: 182-233.
[2] 王树宗, 练永庆, 陈一雕. 气动式水下武器发射装置内弹道数学模型[J]. 弹道学报, 2003, 15(1): 21-26. Wang Shu-zong, Lian Yong-qing, Chen Yi-diao. The Mathemaitc Model of the Underwater Compressed-air Launcher [J]. Journal of Ballistics, 2003, 15(1): 21-26.
[3] 练永庆, 王树宗. 气动式水下武器发射装置节流阀流通面积研究[J]. 弹道学报, 2006, 18(2): 53-57. Lian Yong-qing, Wang Shu-zong. Research on Flow Area of Throttle in Compressed-air Launcher [J]. Journal of Ballistics, 2006, 18(2): 53-56.
[4] 王保国, 刘淑艳, 黄伟光.气体动力学[M]. 北京: 北京理工大学出版社, 2005.
Simulation of Gas-water Recovery Process in Pneumatic Imbalanced Torpedo Launcher
LIAN Yong-qing1, Zhou Hou-cheng2, Wu Kai-feng3, TIAN Bing1
(1. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China; 2. University of National Defence, The People′s Liberation Army of China, Beijing 100091, China; 3. 91341thUnit, The People's Liberation Army of China, Weihai 264200, China)
The gas-water recovery process of non-bubble system has direct influence on the stealth and proportionality of the submarine as it launches a torpedo with pneumatic imbalanced torpedo launcher. To investigate the recovery process, mathematical models of this system are built about timing regulator, bubble-free air flask, relief valve, and so on, and the gas-water recovery process of the non-bubble system is simulated by combining with existing pneumatic imbalanced torpedo launcher models. Comparison of the simulation result with the practical recovery amount shows that the mathematical models are correct, and can be applied to design and analysis of the non-bubble system of pneumatic imbalanced torpedo launcher.
torpedo; submarine; pneumatic imbalance torpedo launcher; non-bubble system; simulation
TJ635
A
1673-1948(2012)03-0220-05
2011-06-09;
2011-08-04.
练永庆(1973-), 男, 博士, 讲师, 主要研究方向为鱼雷动力与发射技术.
(责任编辑: 许 妍)

