空投水雷安全性建模及仿真分析

梁 晶



空投水雷安全性建模及仿真分析

梁 晶

(西北工业大学 航海学院, 陕西 西安, 710072)

为验证空投水雷空中投放的安全性, 建立了其空投过程的运动方程和数学模型, 并按照开伞之前、开伞以后和意外开伞3种情况进行了仿真分析。结果表明, 该种水雷在3种情况下都能确保空投的安全性, 后期进行的实投试验证明了模型和仿真分析的正确性。

空投水雷; 数学模型; 仿真

0 引言

水雷的投放安全性分析是指通过建立水雷投放的安全性分析模型, 研究在投放过程中水雷和水雷之间以及水雷和飞机之间是否发生干涉的问题, 以证明水雷的空投过程对飞机不造成影响, 确保飞机的安全。目前国际上空投水雷普遍采用复式挂架和三联挂架与飞机挂接。如图1所示, 在飞机机翼下一个挂弹架上挂6枚水雷: 前端挂3枚、后端挂3枚。此种方式是投放安全性分析重点考虑的内容。

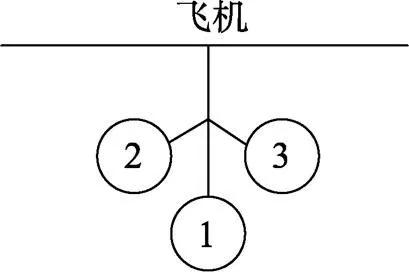
图1 水雷在飞机挂架上的布置图

本文对采用此种挂接方式的空投水雷投放过程进行建模和仿真分析, 由于外挂水雷的空投过程分为开伞前和开伞后2个不同空气动力特性的阶段, 其空气动力模型不同、运动轨迹不同、影响安全性的因素也不相同。因此将空投安全性分析拆分为开伞之前的安全性分析和开伞以后的安全性分析2个阶段, 同时还考虑到飞机航行过程中水雷发生意外开伞的情况下的安全性分析。

1 开伞之前的安全性分析

开伞之前主要考虑水雷投放时前端点与前水雷后端点是否发生干涉, 以及侧向投放水雷的侧面是否会和发射平台挂弹架发生干涉的问题。

首先考虑第一种情况, 即空投后面的水雷时, 后雷前端面、两点在投放过程中是否与前雷的后端面点发生干涉。如图2所示。

图2 上边界点的选取(纵平面)

雷上任意一点在地面系中的坐标[1]

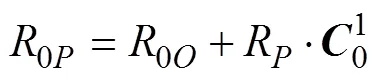
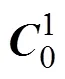
坐标系中,两点之间的距离, 有

2=(X-X)2+(Y-Y)2+(Z-Z)2(2)

这样由弹道曲线[2]和点,点在雷体系中的坐标可以得到点和点的运动曲线, 从而计算出点和前雷后端面点的距离, 同理可计算点和前雷后端面点的距离, 由此可以得出水雷在投放过程中是否发生干涉。由于点和点对称分布, 所以仅计算点即可, 结果见图3。

图3 A点与前水雷后端面距离

由图3可以看出, 水雷在投放过程中, 前端面上点和点与前水雷后端面的距离随时间逐渐增大, 这说明投放水雷的前端面不会和前水雷的后端面发生干涉, 即可以安全投放。这是由于在投放过程中, 水雷由于受到空气阻力的作用, 速度逐渐减小, 而且逐渐低头, 而飞机速度不变, 所以水雷逐渐离开飞机, 即可以安全投放。

考虑第2种情况, 即投放2号或3号水雷后, 水雷侧面是否会和飞机挂弹架发生干涉的问题。如图4所示。

图4 上边界点的选取(横平面)

经过分析可知, 图中的,,这3点如果在水雷投放以后都在向飞机挂弹架相反的方向移动, 则说明水雷不会和挂弹架发生干涉。在计算这种情况的安全性时考虑了空中随机风的影响[3]。以飞机右侧的水雷投放为例进行计算, 结果见图5、图6和图7, 计算中考虑风向分别为0°, 90°, 180°, 270°,风速为10 m/s的随机风的影响。

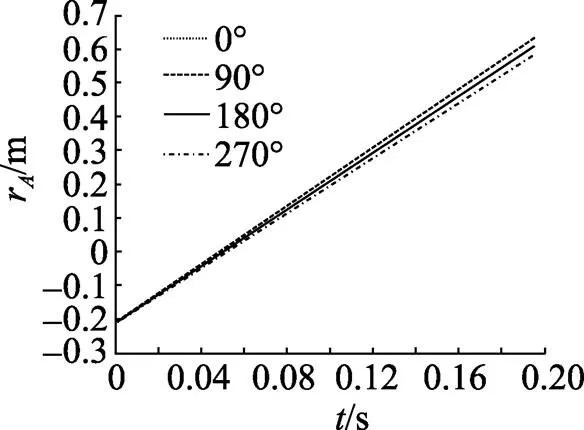
图5 A点位移

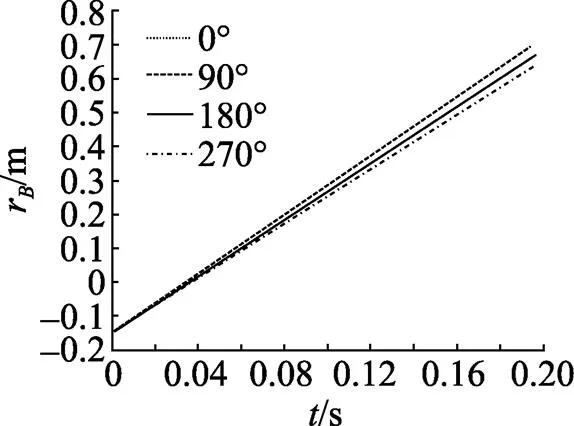
图6 B点位移

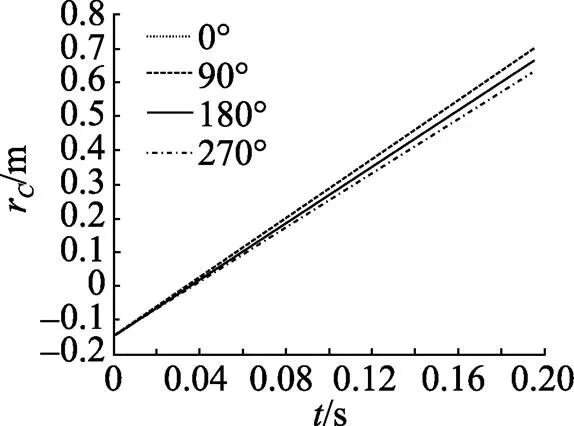
图7 C点位移

由以上各图可以看出, 右侧水雷在投放以后, 由于初始速度的影响, 水雷左侧边界点,,点的位移一直增大, 也就是说, 水雷左侧边界点一直在向离开挂弹架的方向移动, 随机风对水雷边界点的位移有一定的影响, 但没有改变边界点的位移方向, 说明水雷在投放过程中不会和挂弹架发生干涉, 可以安全投放。

2 开伞之后的安全性分析

开伞之后的安全性, 主要考虑在降落伞打开之后, 降落伞是否与飞机以及机上水雷发生干涉的问题。降落伞的外形如图8所示, 可以看出降落伞上的,,点为危险点。这里为了避免建立在降落伞开伞过程中降落伞外形的复杂数学模型[4], 考虑一种保守的做法, 即认为降落伞在开始开伞时就具有如图8所示的外形(单位: mm), 也就是不考虑开伞时降落伞外形的变化[5]。

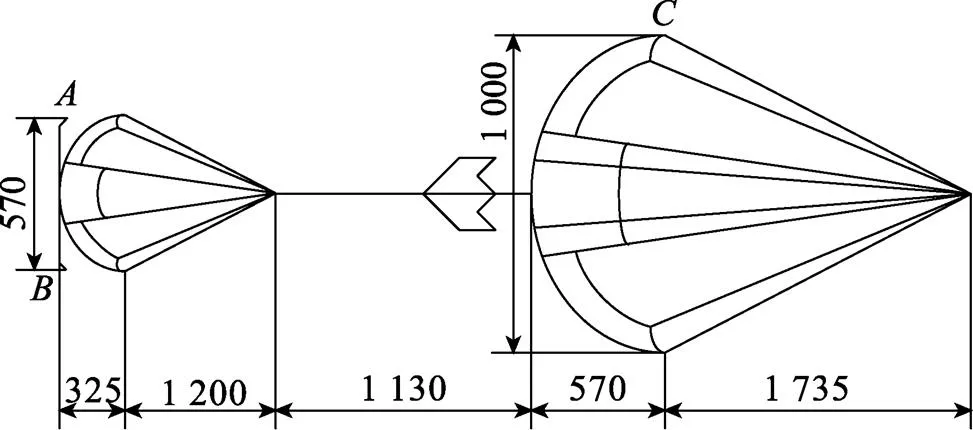
图8 水雷降落伞外形示意图

同理依据式(1)和式(2)可以计算出降落伞上的点,,离飞机下端面的距离, 计算所得距离随时间的变化曲线, 如图9、图10和图11所示。

由以上各图可以看出, 在水雷投放过程中, 降落伞上的,,点与飞机下端面的距离随时间逐渐增大, 这说明降落伞开伞以后不会和飞机下端面发生干涉。

图9 A点到飞机下端面的距离

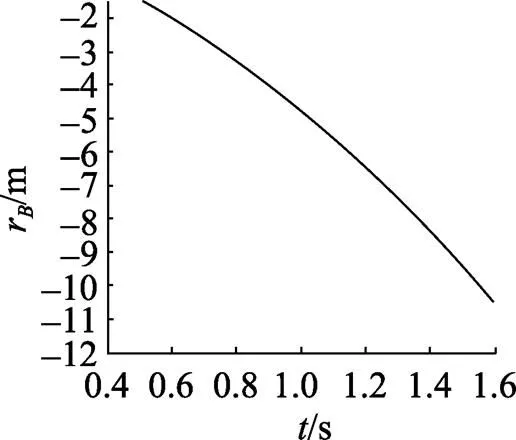
图10 B点到飞机下端面的距离

图11 C点到飞机下端面的距离

3 意外开伞的安全性分析

意外开伞是指, 在飞机挂弹飞行过程中, 开伞系统意外动作, 导致引导伞拉出, 这时主伞包不打开, 引导伞拖动主伞包、雷伞分离装置向后运动, 在拉力达到一定大时雷伞连接器解脱, 主伞包、雷伞分离装置、雷伞连接器在引导伞拉力及自身重力的作用下逐渐离开飞机。意外开伞安全性分析主要是研究意外开伞后, 在主伞包、雷伞分离装置、雷伞连接器以及引导伞在离开飞机的过程中, 是否会和飞机发生干涉的问题。

建立如图12所示的坐标系, 考虑主伞包、雷伞分离装置、雷伞连接器为一刚体, 根据刚体动力学理论, 可以建立如下的动力学方程[6]

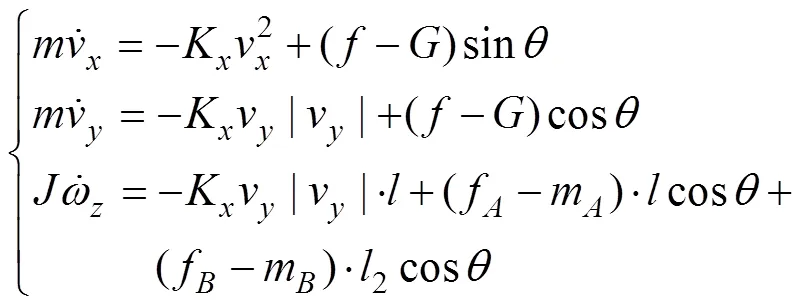
运动学方程

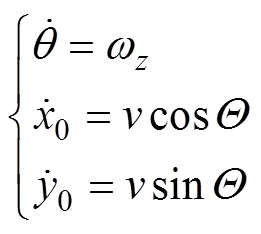
辅助方程

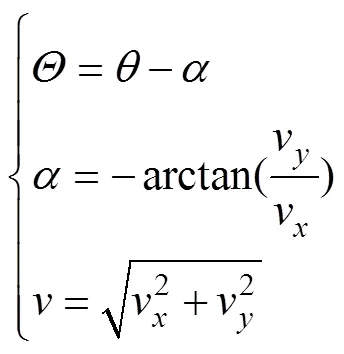
意外开伞安全性分析的危险点为点, 通过仿真点相对于飞机的运动轨迹, 结果见图13。

图13 意外开伞P点运动轨迹

由图13可以看出, 在意外开伞过程中,点与飞机下端面的距离随时间逐渐增大, 这说明降落伞意外开伞以后不会和飞机下端面发生干涉。

4 结束语

通过对空投水雷投放过程进行建模和仿真分析, 可以将空投安全性分析拆分为开伞之前的安全性分析和开伞以后的安全性分析2个阶段, 同时还考虑到飞机航行过程中水雷发生意外开伞的情况下的安全性分析。仿真结果表明, 该种水雷在3种过程中都能确保飞机的安全性。在后期进行的实投试验也验证了该种水雷的空投安全性, 同时也证明了模型和仿真分析的正确性。对空投水雷安全性进行建模和仿真分析可以降低装备型号的研制风险, 减少实投水雷样机数量和实投试验次数, 节省研制费用, 缩短研制周期, 对新型空投水雷的研制具有普遍的参考价值。

[1] 徐惊雷. 径向运动方程在绝对、相对坐标系下的相互转换[J]. 力学与实践, 2007, 29(6): 67-68.

[2] 赵良玉, 杨树兴. 基于Matlab和iSIGHT的弹道曲线拟合方法[J]. 战术导弹技术, 2006, 27(5): 87-90.Zhao Liang-yu, Yang Shu-xing. A Trajectory Fitting Method Based on Matlab and iSIGHT[J]. Tactical Missile Technology, 2006, 27(5): 87-90.

[3] 杜晓旭,宋保维,潘光.带降落伞空投水雷空中弹道仿真分析[J]. 系统仿真学报, 2011, 23(9): 2018-2022.Du Xiao-xu, Song Bao-wei, Pan Guang. Aerial Trajectory Simulation and Analysis of Airdropped Mine with Parachute[J]. Journal of System Simulation, 2011, 23(9): 2018- 2022.

[4] 程文科, 杨小伟, 陈喜兰. 降落伞的运动方程[J]. 航天返回与遥感, 1998, 19(1): 1-4.Cheng Wen-ke, Yang Xiao-wei, Chen Xi-lan. The Equations of Motion for a Parachute[J]. Spacecraft Recovery & Remote Sensing, 1998, 19(1): 1-4.

[5] 刘丹, 王明斐, 李敬伟.物体空间运动轨迹建模优化仿真研究[J]. 计算机与仿真, 2011, 28(11): 87-90.Liu Dan, Wang Ming-fei, Li Jing-wei. Research on Object Space Trajectory Modeling Optimization Simulation[J]. Co­m­puter Simulation, 2011, 28(11): 87-90.

[6] 张相武. 完整力学系统相对运动动力学方程的普遍形式[J].物理学报, 2006, 55(6): 2669-2675.Zhang Xiang-wu. The Universal Forms of the Dynamic Equations of Holonomic Mechanical System in Relative Motion[J]. Acta Physica Sinica, 2006, 55(6): 2669-2675.

Modeling and Simulation of Airdrop Mine Safety

LIANG Jing

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

This paper establishes a motion equation and a mathematical model of airdrop process of a mine to verify the airdrop safety. Three situations are simulated, i.e. the situation before parachute-opening, the situation after parachute-opening, and the situation of accidental parachute-opening. Simulation result shows that airdrop security of the mine can be ensured for the three situations. The following sea trial verifies the correctness of the proposed model and the simulation analysis.

airdropmine; mathematical model; simulation

TJ610

A

1673-1948(2012)03-0171-04

2012-03-08;

2012-04-17.

梁 晶(1981-), 男, 在读硕士, 工程师, 主要研究方向为武器系统与运用工程.

(责任编辑: 陈 曦)