水下目标回波亮点高分辨方位估计与仿真

徐 瑜, 唐 波, 苑秉成



水下目标回波亮点高分辨方位估计与仿真

徐 瑜, 唐 波, 苑秉成

(海军工程大学 兵器工程系, 湖北 武汉, 430033)

水下目标回波亮点识别技术是现代声纳系统与水声对抗的一个极为重要的组成部分。基于单源方位精估的短脉冲切割方法, 对于发射信号为长脉冲以及正横中轴方位下的目标回波亮点方位估计效果较差。因此研究基于多源的水下目标回波亮点高分辨方位估计方法具有重要的应用价值。本文重点研究了水下目标回波亮点高分辨方位估计方法, 首先采用基于共轭倒序阵盖氏圆准则的方法对目标回波进行解相干和亮点数估计, 然后在此基础上进行目标回波空间谱估计以获得目标亮点的方位。在具体仿真过程中, 采用板块元散射方法仿真目标回波, 并在此基础上进行高分辨方位估计, 取得了较好的仿真效果。结果表明, 本文的研究对于正横中轴方位的潜艇目标识别具有一定的应用价值。

水下目标; 高分辨方位估计; 板块元算法; 共轭倒序阵; 盖氏圆; 亮点数估计

0 引言

随着水声技术的发展, 对抗和反对抗技术也相应迅速发展, 各种人工对抗干扰器材在模拟潜艇的辐射噪声、反射回波、运动状态等一系列目标特征方面取得了显著进展。由于鱼雷武器自动检测、跟踪、向目标导引的能力主要依靠声学自导, 因此可以说鱼雷目标识别的主要目的是对抗模拟潜艇特性的声诱饵。尽管声诱饵等对抗器材在鱼雷声自导的发射信号回波等部分特征的模拟越来越真实, 但与真实潜艇相比, 其尺度信息却无法加以精确模拟, 因此研究水下目标回波的空间结构对于水下目标识别技术具有重大意义。

目前, 对水下目标进行尺度识别的一种通用方法是采用双通道短时互谱法, 得到目标的方位走向特征来进行目标尺度识别[1]。但分裂波束互谱法是基于单源方位精估的短脉冲切割方法。当使用较长脉冲时, 由于亮点回波之间会发生重叠, 因此在对目标回波进行时域分割之后仍然会有部分子回波中包含有2个以上的目标方位信息。特别是处在正横方位阵位探测目标的情况下, 基于单源的方位精估方法识别能力就更差。在这种情况下, 就需要采用基于多源的目标回波高分辨方位估计方法, 但该类方法要求目标信源个数已知[2]。基于此, 本文重点研究了水下目标回波亮点数估计方法, 以板块元散射方法仿真的潜艇目标回波为研究对象, 采用基于共轭倒序阵的盖氏圆准则对仿真的目标回波进行解相关和亮点数估计, 并在此基础上进行目标回波空间谱估计。

1 阵列仿真模型

求解目标参数估计问题时, 阵元基阵一般可以具有任意几何形状。绝大多数算法都是针对这种信号源与基阵共处一个平面的情况而提出的。对阵元基阵几何形状的最常见约束是单元阵元均匀地分布在一条直线上, 即均匀分布线列阵。基阵的这种几何构成结构简单, 工程中易于实现。

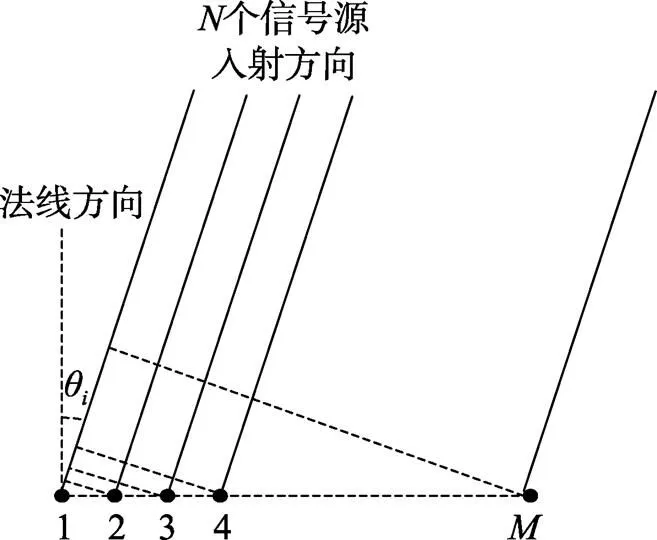
图1 均匀线列阵示意图

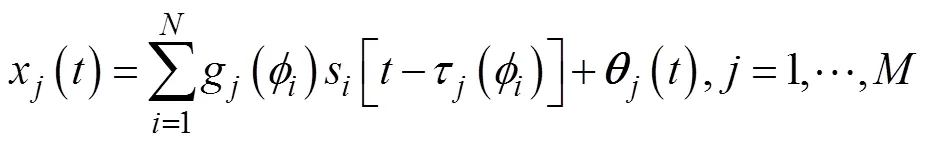
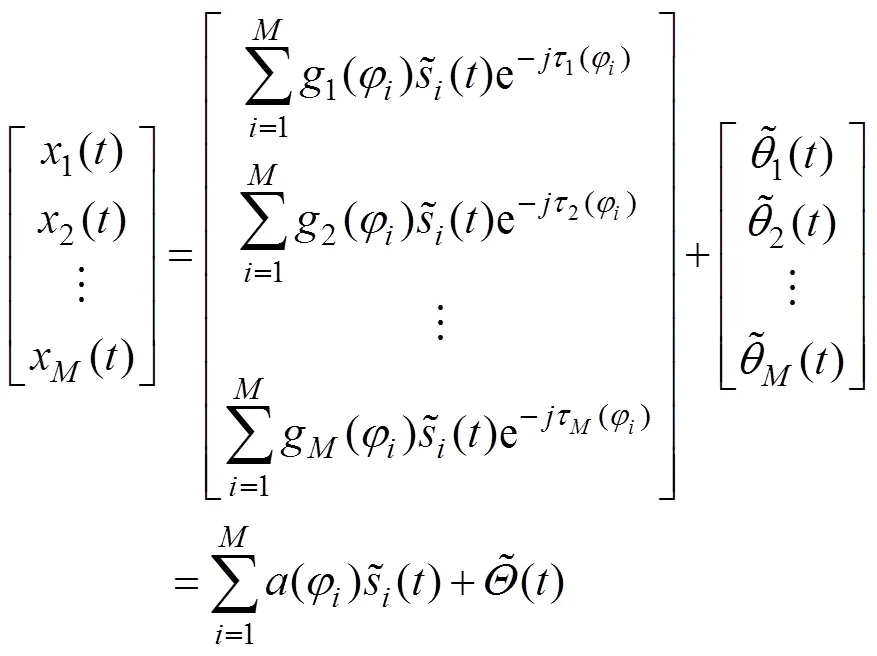
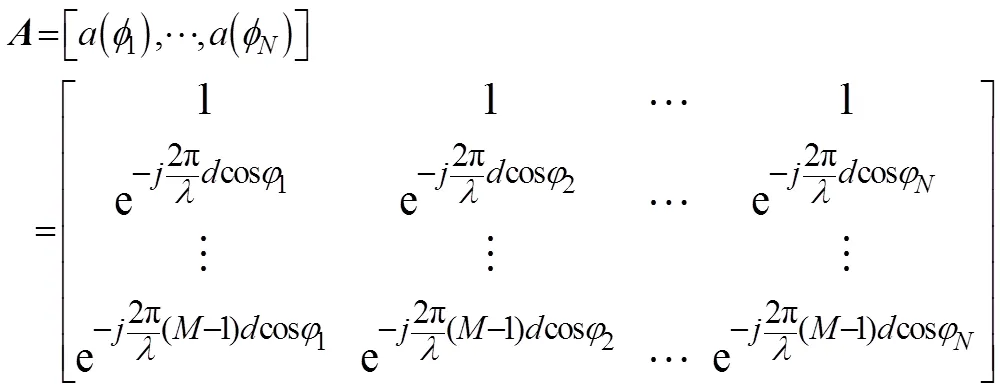
2 盖氏圆准则的目标回波信源数估计

盖氏圆方法是一种不需要具体知道协方差矩阵特征值数值的信号源数目估计方法, 即利用盖氏圆盘定理, 就可以估计出各特征值的位置, 进而估计出信号源。

盖氏圆盘定理: 设=(a)为任一阶复数矩阵, 则的特征值都在复数平面上的个圆盘

|-a|≤R(=1,2,…,) (4)

的并集内, 且这里的

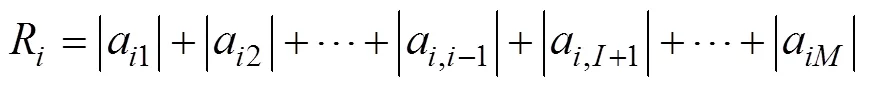
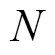
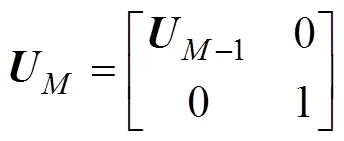
用生成的酉矩阵对接收信号的协方差矩阵作酉变换

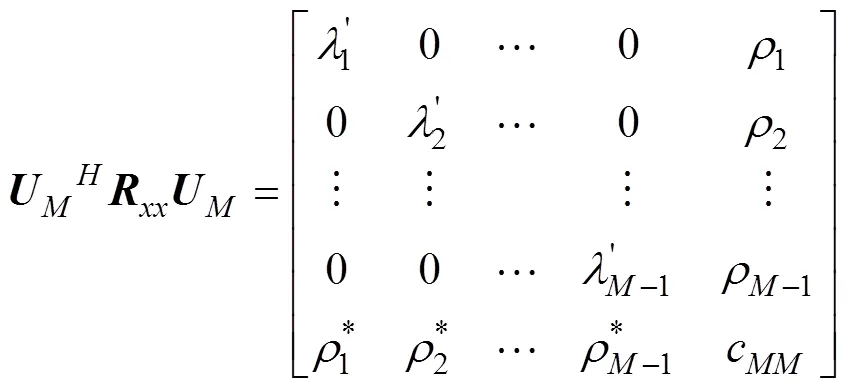
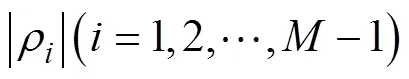
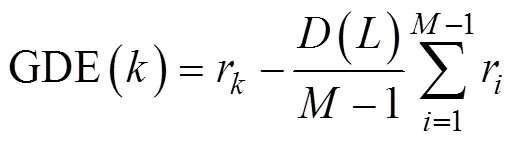
式中,()是一个与快拍数有关的调整因子, 它在0与1之间选取, 当快拍数趋于无穷大时其取0; 在有限取样数据情况下, 其取值应在[0, 1],的取值范围为1,2,…,-2, 当从小到大时, 假设GDE()第1次出现负数时的数为0, 则信号源数为=0-1。

理想情况下均匀线列阵信号的协方差矩阵具有Toeplitz的性质。但是由于各亮点回波信号之间存在相关性, 从而导致矩阵秩的退化, 信号协方差矩阵将不再是Toeplitz矩阵。因此, 如果使阵列信号协方差矩阵逼近与其最为相似的Toeplitz矩阵, 就可以去除各亮点信号之间的相关性。

设接收线列阵输出信号的协方差矩阵为

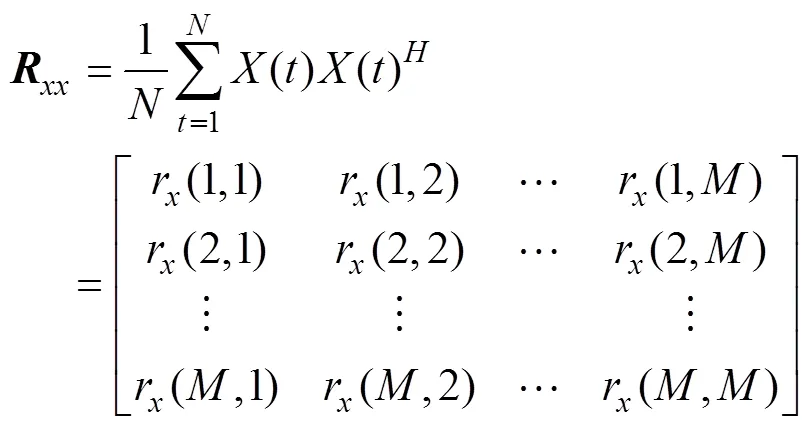
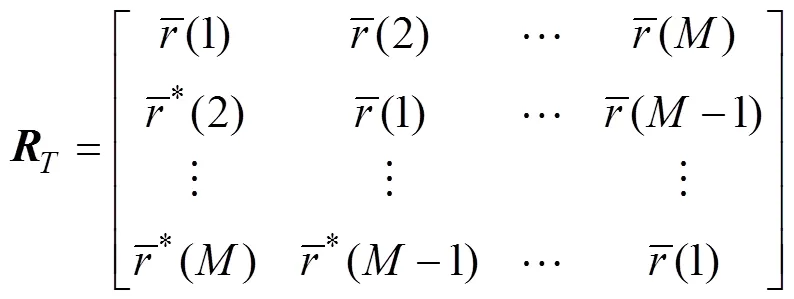
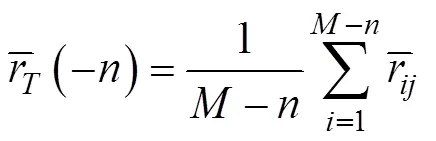
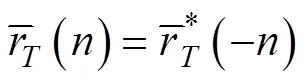
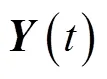
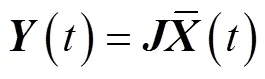
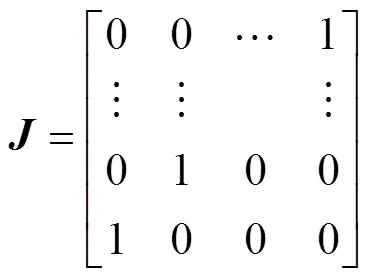
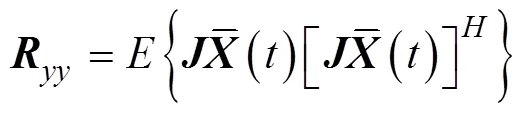
该方法主要分为以下4步。

2) 把原始信号协方差矩阵与共轭倒序信号协方差矩阵的和作为去相关后的协方差矩阵;

3) 对阵列协方差矩阵用Toeplitz近似进一步去除信号之间的相关性;

3 相干源高分辨方位估计

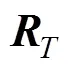
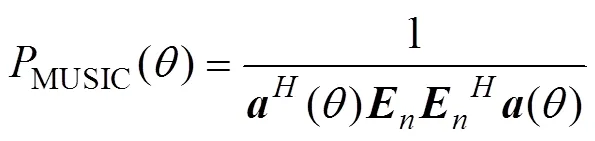
4 数值计算与仿真

4.1 潜艇目标几何建模

为方便计算, 本文以标准潜艇模型(BeTSSi- Sub)为主要研究对象[4]。该模型将潜艇目标模拟为几个简单形状目标的组合, 用半椭球体来模拟艇艏, 圆柱体模拟艇体, 艇艉为圆锥体, 指挥台围壳前半部为半椭圆体, 后半部为锥体, 水平艉舵与垂直艉舵端面均为前半部半椭圆体, 后半部锥体。具体参数为: 艇全长62m, 艇体直径7.5 m, 前端半椭球体的长度为7m, 中段圆柱体的长度为44.6 m, 后端锥体的长度为11.4 m。舰桥中心距艇艏顶点22.85m处, 前端半椭球体长半轴为3.85 m, 短半轴为2.2m。在实际建模时, 先借助AutoCAD软件对目标进行几何建模, 然后再将数据导入Ansys软件进行网格划分。图2给出了AutoCAD建模后的结果, 并根据声纳系统与目标之间的相对位置关系, 建立了直角坐标系。

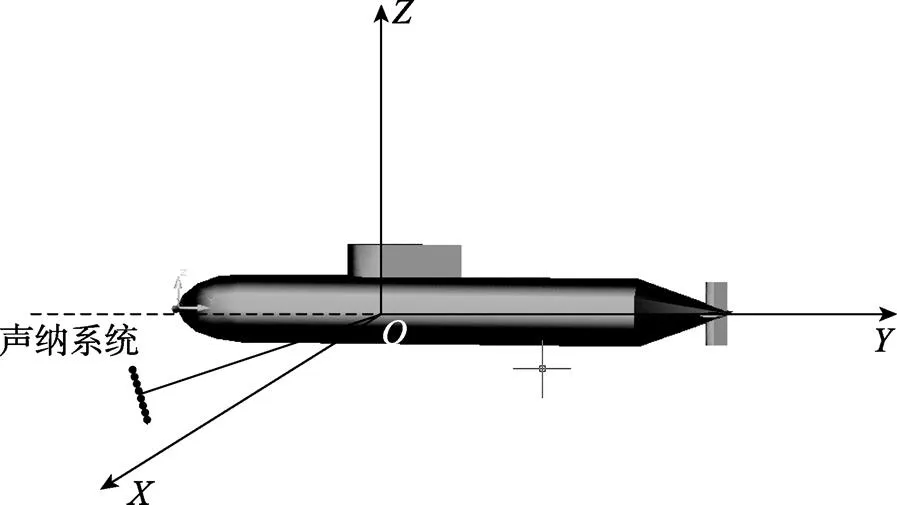
图2 潜艇目标几何模型

4.2 仿真结果与分析

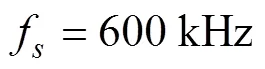
图3给出了采用板块元散射算法仿真的潜艇目标回波, 从图中可以看出, 由于目标各亮点回波之间的时延非常小, 目标回波在时域没有体现出明显的包络起伏。图4分别给出了采用基于共轭倒序阵盖氏圆准则的盖氏圆半径分布图(以其中最大的盖氏圆半径为基准对各盖氏圆半径作归一化处理)和使用MUSIC方法得到的空间谱分布图, 从盖氏圆半径分布图可以看出, 目标回波体现了2个较强亮点的方位信息, 从亮点的方位来进行分析, 分别对应的是舰桥亮点和艇艉亮点。

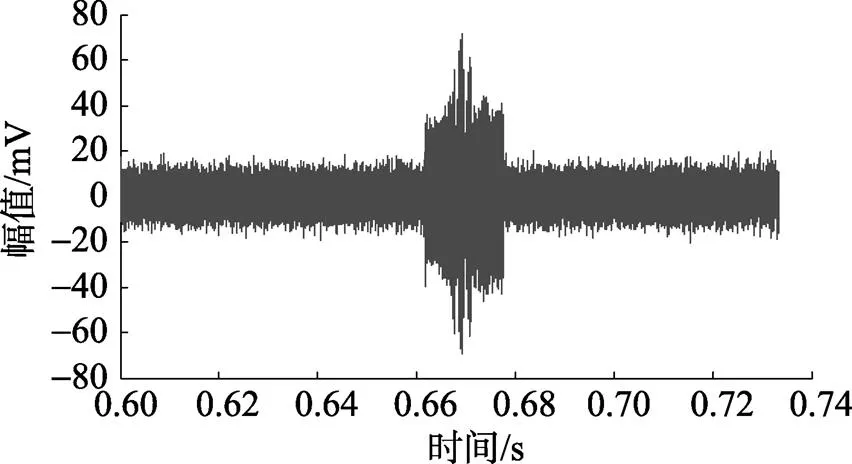
图3 正横中轴情况下的潜艇目标仿真回波

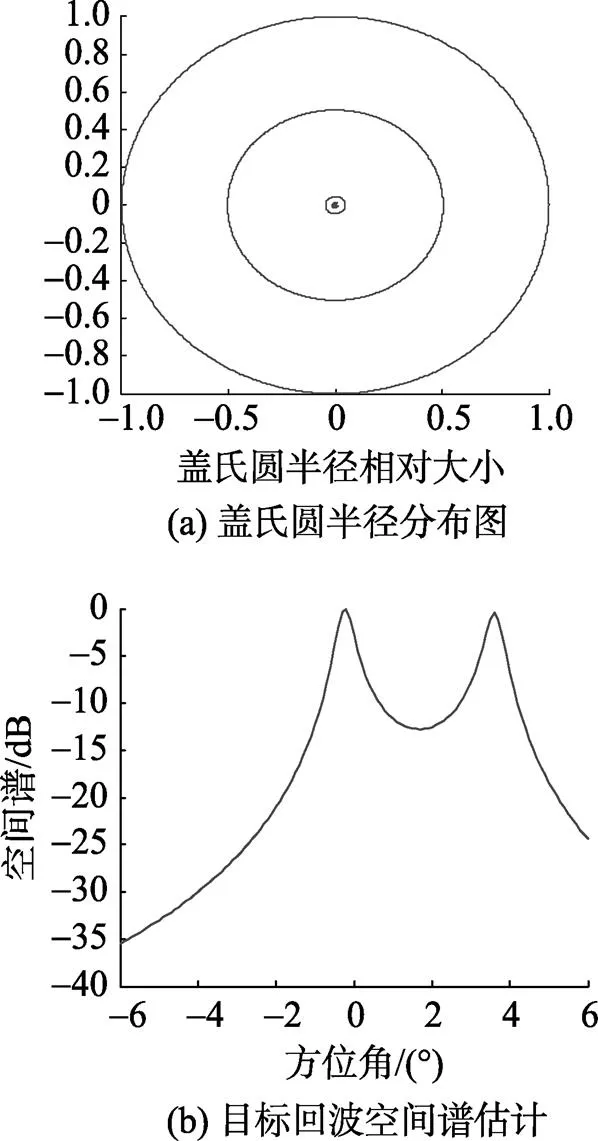
图4 基于共轭倒序阵盖氏圆准则的亮点数和空间谱估计

5 结束语

分裂波束互谱法是基于单源方位精估的短脉冲切割方法。当使用较长脉冲时, 由于亮点回波之间会发生重叠[7], 采用分裂波束互谱法进行方位走向估计就会产生较大的误差。基于此, 本文重点研究了基于共轭倒序阵盖氏圆准则进行水下目标回波亮点数和空间谱的估计方法, 采用板块元散射算法仿真的正横方位下的标准潜艇回波数研据为究对象进行了亮点数估计与空间谱估计的仿真试验。仿真取得了较好的效果。本文的研究对于正横中轴方位的潜艇目标尺度识别具有一定的应用价值。

[1] 刘朝晖, 付战平, 王明洲. 基于方位走向法和互谱法的水中目标识别[J]．兵工学报, 2006, 27(5): 932-935. Liu Zhao-hui, Fu Zhan-ping, Wang Ming-zhou. Underwater Target Identification Based on the Methods of Bearing and Cross-spectrum[J].Acta Armamentarii, 2006, 27(5): 932-935.

[2] 赵水兵, 颜冰, 樊书宏. 水下目标空间源数特征提取与识别方法[J]．声学技术, 2008, 27(3): 342-346. Zhao Shui-bing, Yan Bing, Fan Shu-hong. A Method of Space Source Number Feature Extraction and Automatic Recognition for Underwater Targets[J]. Technical Acous- tics, 2008, 27(3): 342-346.

[3] 胡隽, 吴南润. 基于共轭倒序阵盖氏圆准则的相关信源数估计研究[J]. 探测与控制学报, 2007, 29(6): 16-20. HuJun, Wu Nan-run. Research on the Gerschgorin Radii Estimator of Coherent Signals Based on Reverse Conjugate Array[J]. Journal of Detection & Control, 2007, 29(6): 16-20.

[4] 卜考英. 水下目标回波特性预报模型验证研究[D]. 上海: 上海交通大学，2006. Bo Kao-ying. Validation Research on the Echo Characteristics Prediction Model of Underwater Target[D]. Shang Hai: Shang Hai Jiao Tong University, 2006.

[5] 范军, 汤渭霖. 声纳目标强度(TS)计算的板块元方法[J]. 声学技术, 1999, 33(增刊): 31-32. Fan Jun, Tang Wei-ling. The Planar Element Method for Computing Target Strength(TS) of Sonar[J]. Technical Acoustic, 1999, 33(sup): 31-32.

[6] 刘成元, 张明敏, 程广利. 一种改进的板块元目标回声计算方法[J]. 海军工程大学学报, 2008, 20(1): 25-31. Liu Cheng-yuan, Zhang Ming-min, Cheng Guang-li. Improved Planar Element Method for Computing Target Echo[J]. Journal of Naval University of Engineering, 2008, 20(1): 25-31.

[7] 汤渭霖. 声纳目标回波的亮点模型[J]. 声学学报, 1994, 19(2): 92-100.Tang Wei-lin. Highlight Model of Echoes From Sonar Targets[J]. Acta Acustica, 1994, 19(2): 92-100.

High-Resolution DOA Estimation Algorithm for Underwater Target Echo Highlight with Simulation

XU Yu, TANG Bo, YUAN Bing-cheng

(Department of weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

Underwater target echo highlight identification technology is a very important part for modern sonar system and underwater acoustic countermeasure. However, when transmit signal is long pulse or the sonar system is located at abeam bearing, the estimation algorithm of underwater target echo highlight direction of arrival(DOA) based on single-source based short pulse split theory is inefficient. Therefore, a multi-source based high-resolution DOA algorithm for underwater target echo highlight is proposed in this paper. The received echo signal is de-correlated and the echo highlight number is estimated by the Gerschgorin radii-based estimator based on the reverse conjugate array, and then the underwater target echo highlight direction is estimated with the space spectrum estimation method. Moreover, underwater target echo is simulated with the planar element method for high-resolution DOA estimation. Simulation verifies the proposed method is efficient for recognition of submarine target at abeam bearing.

underwater target; high-resolution direction of arrival(DOA) estimation; planar element method; reverse conjugate array; Gerschgorin radii; highlight number estimation

TJ630.34; TN911

A

1673-1948(2012)03-0190-05

2011-08-31;

2011-09-26.

徐 瑜(1983-), 男, 在读博士, 研究方向为军用目标特性与制导技术.

(责任编辑: 杨力军)