基于Jacobi几何向量的多AUV编队控制方法

张 静, 杨惠珍, 郝莉莉, 康凤举



基于Jacobi几何向量的多AUV编队控制方法

张 静1,2, 杨惠珍1,2, 郝莉莉1,2, 康凤举1,2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 水下信息与控制重点实验室, 陕西 西安, 710072)

研究了多自主水下航行器(MAUV)系统的水平面动力学建模和系统编队控制问题。从单个自主水下航行器的动力学和运动学模型出发, 通过引入Jacobi几何向量建立了MAUV系统的水平面动力学模型; 结合典型水下航行器全方位智能导器(ODIN)的流体动力参数, 将系统模型解耦为3个线性子系统——编队队形、编队运动(即编队中心点的运动)及航行器转向子系统, 并采用线性状态反馈法设计了运动控制器和转向控制器。仿真结果表明, 该算法可以控制MAUV系统在保持编队队形的基础上跟踪已知路径。

多自主水下航行器(MAUV); 编队控制; Jacobi几何向量; 全方位智能导航器(ODIN); 线性反馈控制

0 引言

自主水下航行器(autonomous underwater vehicle, AUV)是一种智能化、自主航行、可根据任务使命要求进行模块优化组合、实现多种功能的集成系统[1], 其应用领域遍及海洋水文探测、海洋石油勘探与开采、水下考古和水下搜救等。多自主水下航行器（MAUV）系统通过各AUV间的协调合作可更可靠、快速地完成工作任务。因此受到国内外学者的高度重视。编队控制作为研究MAUV系统的基础性问题, 近年来取得了大量的研究成果[2-10]。

目前编队控制常见做法是将控制对象的运动模型简化为2阶粒子模型[2-8]。由于控制对象的实际模型远比2阶微分方程复杂, 因而编队控制方法在实际工程应用中仍面临相当大的挑战。文献[9]利用AUV三自由度水平面运动学方程, 根据领航者的位置和转向信息设计了一个虚拟leader, 并以其信息为参考, 设计了主从式队形控制策略。文献[10]研究了一种鱼雷型水下航行器水平面2D运动模型, 并基于人工势函数设计了多航行器的编队控制。文献[11]考虑小型无人机六自由度非线性模型, 利用滑模控制算法实现了多无人机的任意编队控制。文献[12]建立(remotely operated vehicle, ROV)水下航行器的六自由度空间动力学方程, 提出具有通信约束的分布式水下航行器群编队控制算法。文献[13]利用水下航行器全方位智能导航器(omni-directional intelligent navigator, ODIN)六自由度动力学模型设计比例-微分控制器, 实现了多航行器的编队控制。

模型的复杂性使设计的编队控制器在理论证明上有一定困难。本文从单个AUV的动力学模型出发, 将文献[14]中用于粒子编队系统的Jacobi图形理论推广到MAUV编队系统, 建立了编队系统的动力学模型。该模型描述了MAUV编队系统的编队队形和编队中心点运动过程。将ODIN的流体动力学参数代入该模型[15], 得到了3个解耦的线性子系统, 即编队队形子系统、编队中心运动子系统和AUV转[U4] 子系统。采用线性反馈控制方法设计了各子系统的控制律。仿真结果表明，该方法可控制MAUV编队系统跟踪指定路径并同时保持预定的队形。

1 单个AUV三自由度模型

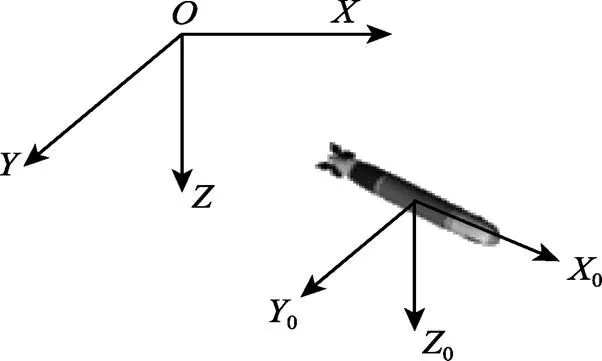
图1 载体坐标系和地面坐标系

Fig.1 Body-fixed and earth-fixed reference coordinates

则AUV三自由度水平面运动学和动力学方程

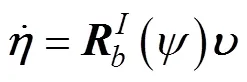
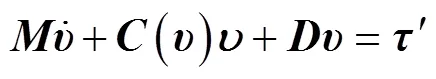
载体坐标系下航行器的轴向、侧向及偏航速度矢量定义为

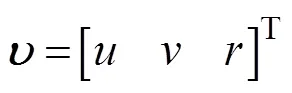
载体坐标系到地面坐标系的坐标转换矩阵

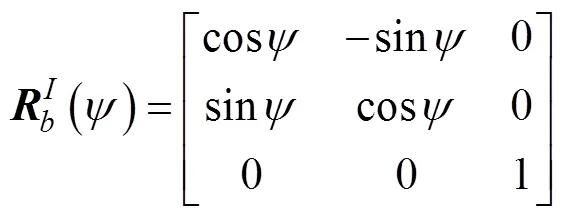
科里奥利-向心矩阵

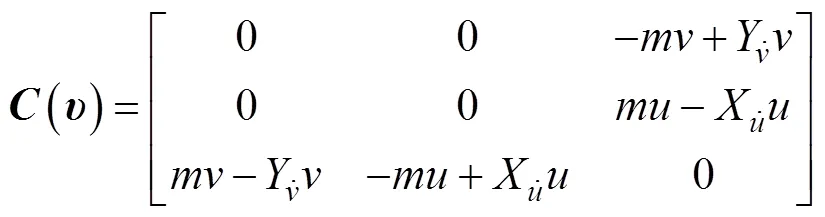
系统惯性矩阵

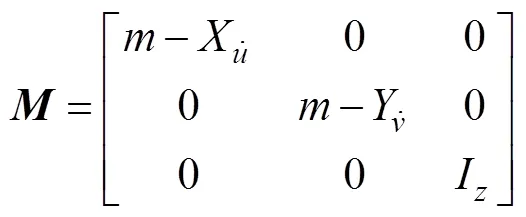
航行器侧向力、轴向力及偏航力矩的外部控制输入

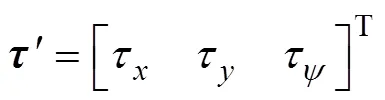
水动力阻尼矩阵

2 Jacobi向量

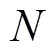
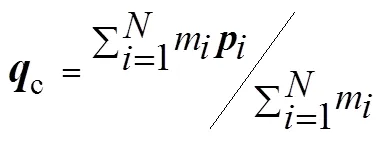
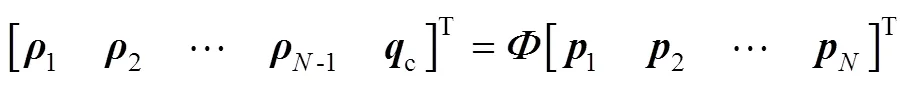
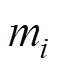
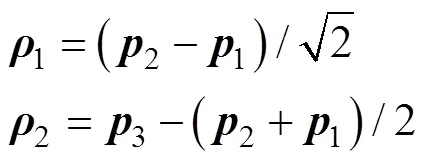
队形中心点位置

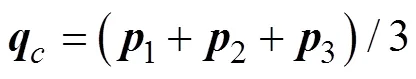
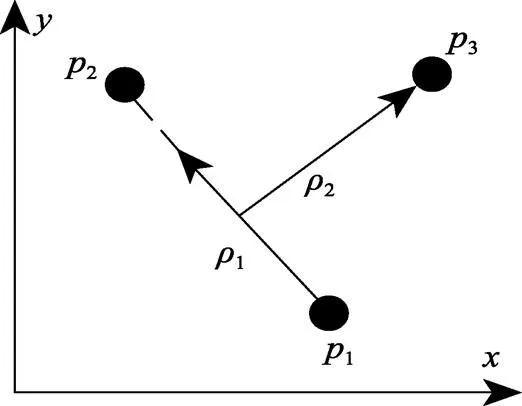
图2 用Jacobi向量描述由3个AUV组成的编队系统队形

3 MAUV编队系统动力学模型

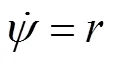
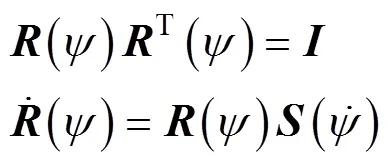
同理, 可将式(2)写成

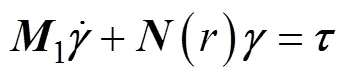
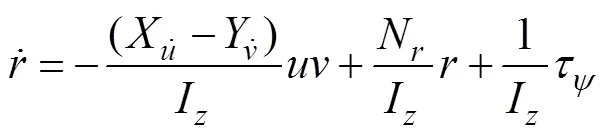
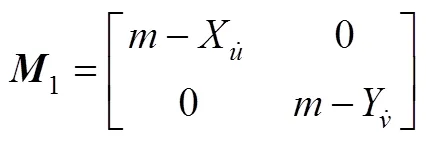
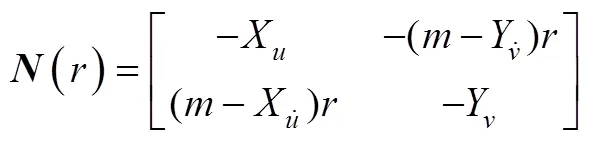
式(13)两边取微分可得

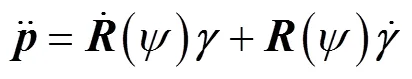
将式(14)~式(16)代入式(20), 且定义

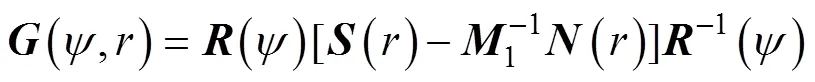
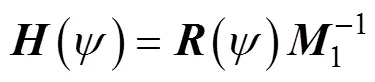
则, 式(20)可写为

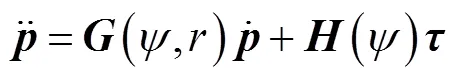
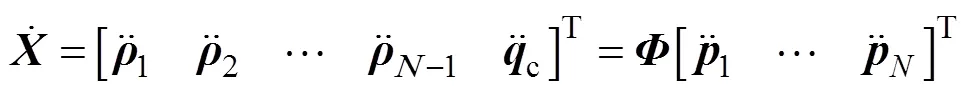
应用式(23)可得MAUV编队系统动力学模型

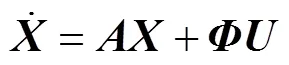
其中

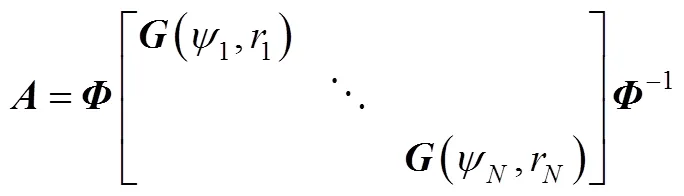
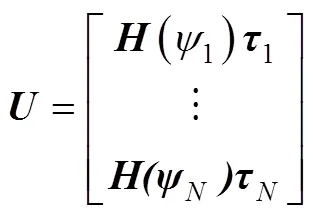
下节将航行器ODIN的流体动力学参数代入式(25), 得到多ODIN编队系统的动力学模型, 然后进行控制律设计。

4 ODIN编队控制律设计

4.1 多ODIN编队系统动力学方程

ODIN是美国夏威夷大学研制的一种球形水下航行器, 如图3所示。

则可将系统(25)解耦为编队队形方程和中心

点运动方程

航行器的转向动力学方程

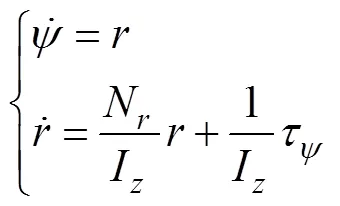
显然, 式(29)，式(30)为线性方程。所以多ODIN编队系统是个可解耦的线性系统, 可分别设计控制律控制Jacobi向量和队形中心点位置向量。

4.2 编队控制律设计

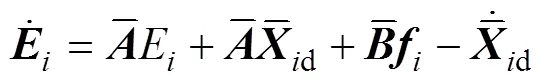
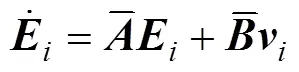
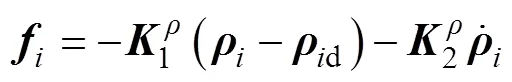
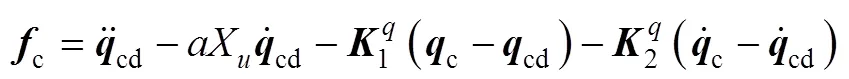
4.3 转向控制律设计

不妨假设航行器不受侧向力, 即=0, 且令

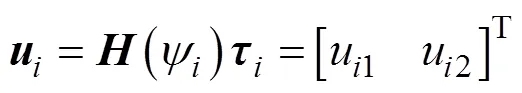
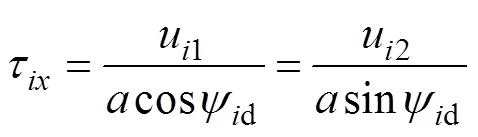
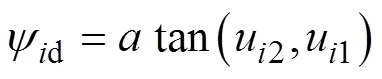
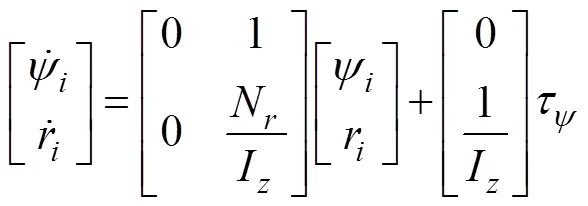
易验证该系统完全可控可观测, 所有由线性状态反馈得偏航力矩控制律为

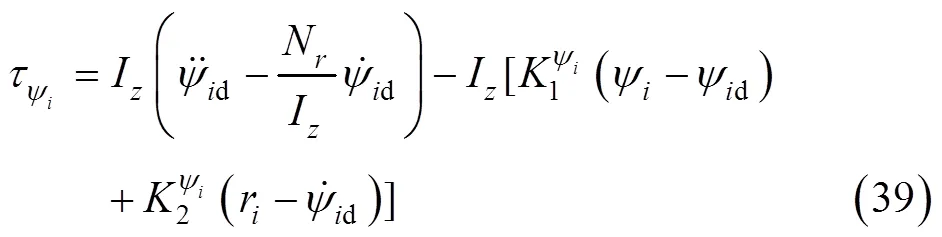
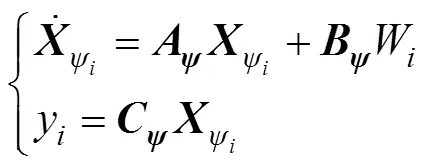
该系统完全可控可观测, 故卡尔曼滤波器方程

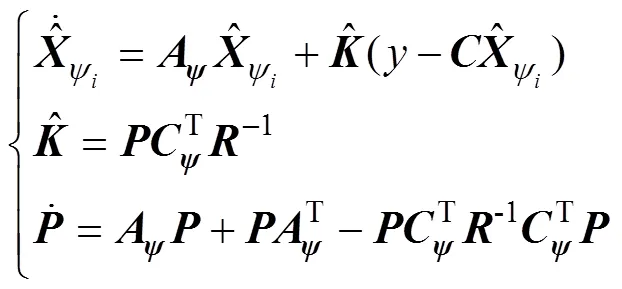
5 仿真试验

5.1 试验1

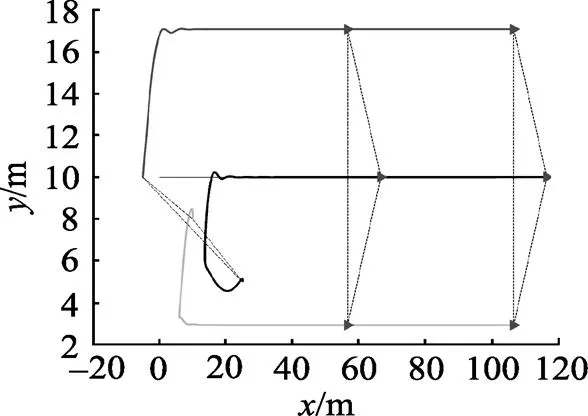
图4 跟踪直线时编队系统的运动轨迹

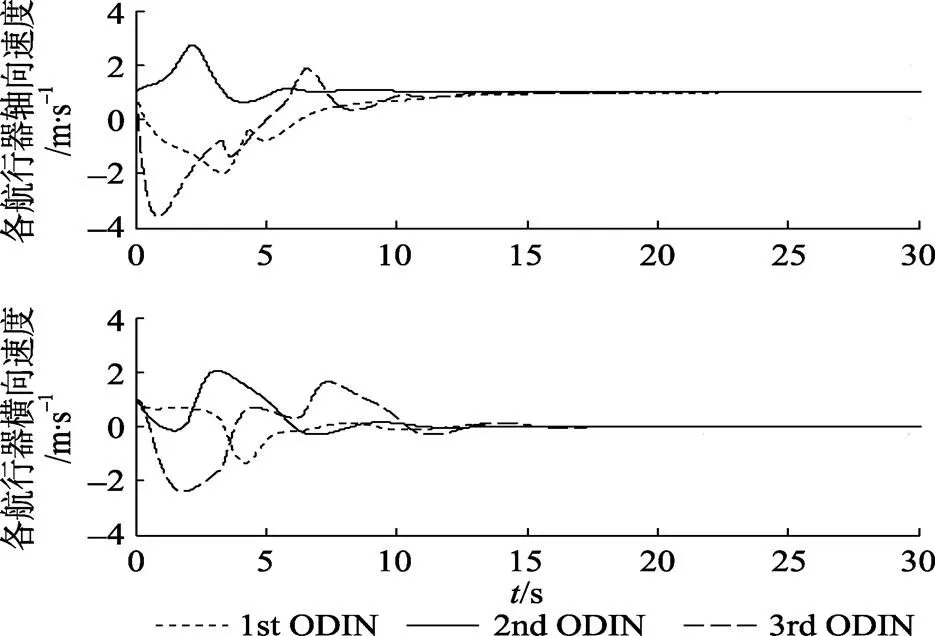
图5 航行器的轴向速度及横向速度

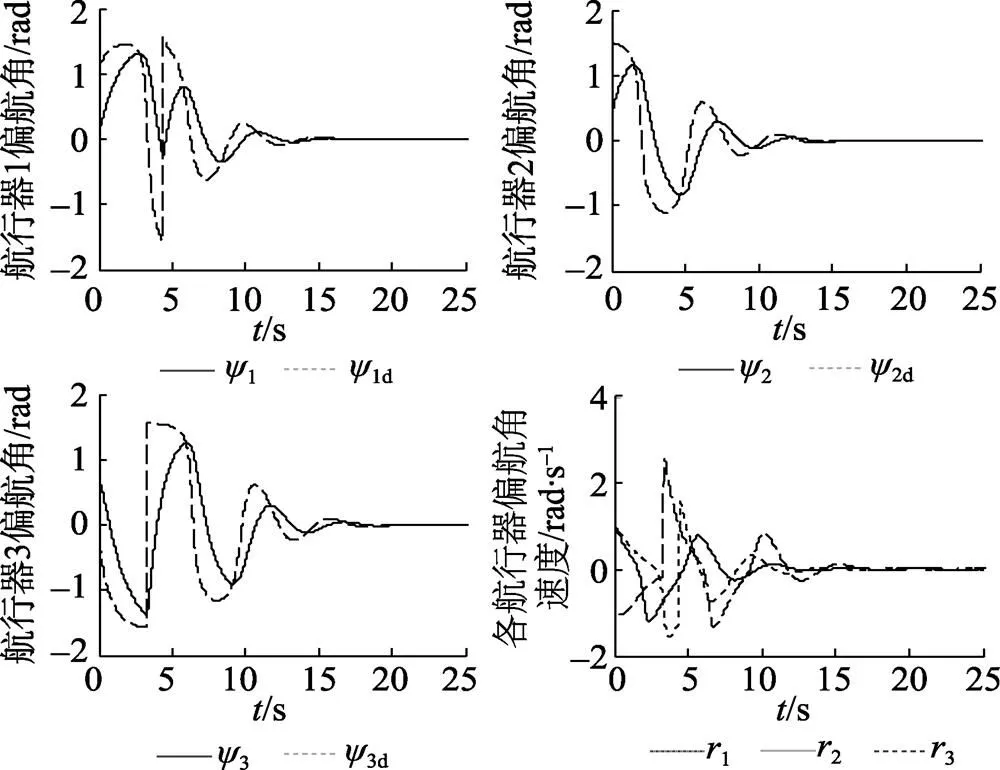
图6 航行器的偏航角及偏航角速度

5.2 试验2

系统由6个ODIN组成, Jacobi几何向量定义为

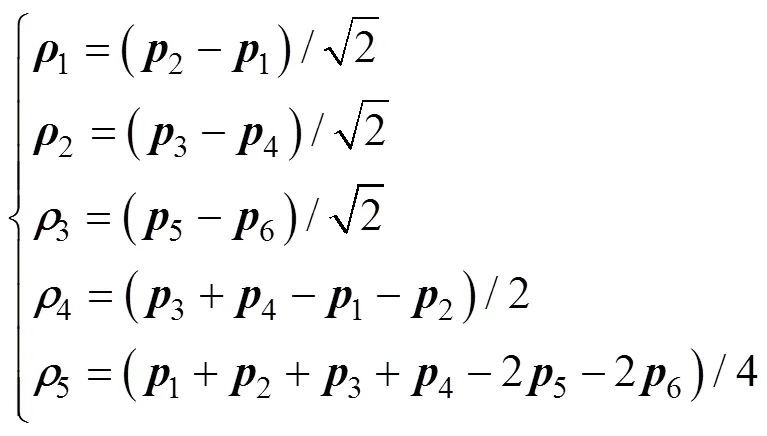
设Jacobi几何向量的期望值为即期望的编队队形为如图7所示的六边形。跟踪轨迹为正弦曲线。

图8所示的仿真结果表明，每个航行器都很好地完成了轨迹跟踪。

6 结束语

本文从水下航行器的三自由度水平面运动学和动力学方程出发, 基于Jacobi几何向量建立了MAUV系统的动力学模型。由于航行器的对称性, 多ODIN系统的动力学模型解耦为编队队形、编队中心点运动及转[U5] 运动3个独立的线性子系统, 用线性状态反馈设计方法实现了各子系统的控制律设计。仿真结果表明, 应用此算法可实现多ODIN系统的队形保持和路径追踪。

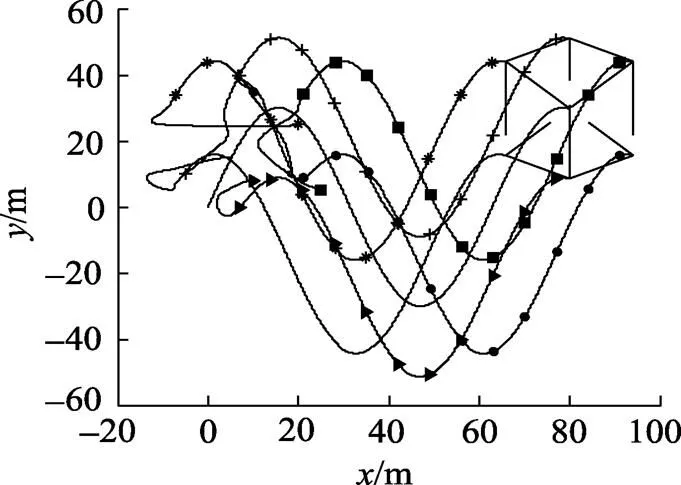
图8 跟踪正弦曲线时编队系统的运动轨迹

[1] 王银涛, 郑美云, 严卫生. 一种新的AUV路径跟踪控制方法[J]. 西北工业大学学报, 2009, 27(4): 517-520. Wang Yin-tao, Zheng Mei-yun, Yan Wei-sheng. A New Meth- od of Path Following Control of AUV (Autonomous Under- water Vehicle)[J]. Journal of Northwestern Polythechnical University, 2009, 27(4): 717-520.

[2] Lewis M, Tan K H. High Precision Formation Control of Mobile Robots Using Virtual Structures[J]. Autonomous Robots, 1997, 4(4): 387- 403.

[3] Zhang F, Leonard N E. Cooperative Kalman Filters for Coo- perative Exploration[C]//Proceedings of 2008 American Con- trol Conference.Washington, 2008: 2654-2659.

[4] 李向舜, 方华京. 基于分数阶PDμ控制器的群体编队控制[J]. 华中科技大学学报: 自然科学版, 2009, 37(10): 32-35. Li Xiang-shun, Fang Hua-jing. PDμ-based Controller For- mation Control of Networked Swarm Agents[J]. Journal Hua- zhong University of Science and Technology: Natural Scien- ce Edition, 2009, 37(10): 32-35.

[5] 陈杨杨, 田玉平. 多智能体沿多条给定路径编队运动的有向协同控制[J]. 自动化学报, 2009, 35(12): 1541- 1549. Chen Yang-yang, Tian Yu-ping. Directed Coordinated Con- trol for Multi-agent Formation Motion on a Set of Given Curves[J]. Acta Automatica Sinica, 2009, 35(12): 1541-1549.

[6] Cui R, Ge S S. Ren B. Synchronized Altitude Tracking Con- trol of Multiple Unmanned Helicopters[C]//Proceedings of 2010 American Control Conference, 2010: 4433- 4438.

[7] 张飞, 陈卫东. 移动机器人编队自修复的切换拓扑控制[J].控制理论与应用, 2010, 27(3): 289-295. Zhang Fei, Chen Wei-dong. Switched Topology Control for Self-healing of Mobile Robot Formation[J]. Control Theory & Applications, 2010, 27(3): 289-295.

[8] Zhang F. Cooperative Shape Control of Particle Forma- tions[C]//Proceedings of the 46th IEEE Conference on Deci- sion and Control, 2007: 2516-2521.

[9] Cui R, Ge S S, How B E, et al. Leader-follower Formation Control of Underactuated AUVs with Leader Position Mea- surement[C]//Proceedings of IEEE International Conference on Robotics and Automation, 2009: 979-984.

[10] Li J H, Jun B H, Lee P M. Formation Control of Multiple Un- deractuated AUVs[C]//Proceedings of IEEE Oceans. Europe, 2007: 1-5.

[11] Fahimi F. Full Formation Control for Autonomous Helicopter Groups[J]. Robotica, 2008, 26(2): 143-156.

[12] 杨波, 方华京.具有通信约束的分布式水下航行器群编队控制[J]. 华中科技大学学报: 自然科学版, 2009, 37(2): 57-60. Yang Bo, Fang Hua-jing. Distributed-control of Maneuvers of Underwater of Underwater Vehicle Groups with Communi- cation Constraint[J]. Journal Huazhong University of Science and Technology: Natural Science Edition, 2009, 37(2): 57-60.

[13] Hou S P, Cheah C C. PD Control Scheme for Formation Con- trol of Multiple Autonomous Underwater Vehicles[C]//Pro- ceedings of IEEE/ASME International Conference on Advan- ced Intelligent Mechatronics. Singapore, 2009: 356-361.

[14] Zhang F, Goldgeler M, Krishnaprasad P S. Control of Small Formations Using Shape Coordinates[C]//Proceedings of the 2003 IEEE International Conference on Robotics and Auto- mation. Taipei, 2003: 14-19.

[15] Choi S K, Tahashige G Y, Yuh J. Experimental Study on an Underwater Robotic Vehicle: ODIN[C]//Proceedings of the 1994 Symposium on Autonomous Underwater Vehicle Tech- nology. Cambridge, 1994: 79-84.

[16] Fossen T I. Guidance and Control of Ocean Vehicles[M]. Chichester: John Wiley and Sons, 1994.

[17] Antonelli G. Underwater Robits-Motion and Force Control of Vehicle-Manipulator Systems[M]. 2th ed. Berlin: Springer- Verlag, 2006.

A Formation Control Algorithm for Multiple Autonomous Underwater Vehicles Based on Jacobi Shape Theory

ZHANG Jing1,2, YANG Hui-zhen1,2, HAO Li-li1,2, KANG Feng-ju1,2

(1.College of Marine Engineering, Northwestern Polythechnical University, Xi′an 710072, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710072, China)

Dynamics modeling and formation control of multiple autonomous underwater vehicles (MAUVs) system are addressed. Based on dynamics and kinematics models of a single AUV, a horizontaldynamics model of MAUV system is established by applying the Jacobi geometric vector. With the hydrodynamic parameters of the typical underwater vehicle’s omni-directional intelligent navigator (ODIN), the formation dynamics model is reasonably simplified and decoupled into three linear subsystems——formation shape, formation movement (i.e. movement of the formation center), and Vehicle orientation subsystem. Motion controller and steering controller are designed for the decoupled linear subsystem by using the linear state feedback approach. Simulation results demonstrate that the algorithm can control the formation center of MAUV system to track known path while keeping formation shape.

multiple autonomous underwater vehicle(MAUV); formation control; Jacobi geometric vector; omni-directional intelligent navigator(ODIN); linear feedback control

TJ630.33; U674.76

A

1673-1948(2012)02-0111-06

2011-07-03;

2011-10-31.

水下信号与控制重点实验室基金资助(9140C2305041001).

张 静(1983-), 女, 在读硕士, 研究方向为水下航行器协同控制.

(责任编辑: 杨力军)