一种橡胶隔振圈动刚度计算方法

金 晶, 张振山, 熊 鑫



一种橡胶隔振圈动刚度计算方法

金 晶1, 张振山1, 熊 鑫2

(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 海军工程大学 电气与信息学院, 湖北 武汉, 430033)

在以往对橡胶隔振器动刚度计算方法研究的基础上, 提出了一种将隔振器主要部件作为一体进行动刚度仿真计算的方法。建立了包含金属和橡胶部件的橡胶隔振圈有限元模型, 根据隔振圈在不同方向上的实际受力情况对隔振圈施加不同频率的正弦激励, 仿真计算得到了隔振圈不同方向上的动刚度。通过与隔振圈静刚度和橡胶材料动刚度的比较, 得出了动刚度的变化规律, 为发动机的振动分析和橡胶隔振圈的简化提供了参考。

橡胶隔振圈; 动刚度; 有限元模型; 仿真

0 引言

随着科技的进步, 评价一款发动机是否优秀,其指标已经从功率、扭矩是否满足需求发展为振动、噪声是否足够小。因此发动机整体的噪声、振动和刺耳声(noise vibration harshness, NVH)指标已成为评价发动机好坏的重要因素。尤其是在潜艇、鱼雷等对振动噪声要求非常严格的装备中, 发动机振动噪声性能已经成为筛选发动机的决定性条件之一。

橡胶材料由于隔振降噪性能良好、成本低廉而在各种设备中广泛应用。目前在水下航行器中广泛使用的斜盘发动机, 其隔振装置就是橡胶隔振圈。而橡胶隔振圈的隔振能力直接取决于它的动静态特性, 其中动态特性是橡胶悬置的一种重要特性,具有复杂的非线性。因此,需要在模拟的发动机振动激励条件下,研究橡胶悬置在不同激励频率和激励振幅下的动静态特性及其相互关系。目前可参考文献主要集中在隔振器的实验分析[1-4]以及单独对橡胶材料的仿真分析上[5-6], 将隔振器作为整体进行动刚度计算的文献很少。

文中使用有限元方法建立了一型发动机隔振圈的有限元模型。并在理论分析和仿真计算的基础上提出了一种可行的振动状态下计算橡胶减振器整体动刚度的方法, 为进一步对发动机振动性能的分析和优化提供重要数据参考。

1 动刚度计算理论

机械设计中, 在分析机械振动引起结构的动态位移及其对机器工作能力的影响时, 往往使用动刚度来评价。结构动刚度对于不同的振动, 其数值各不相同, 但都取决于激励频率和结构本身的参数如质量、刚度和阻尼等。对于自由振动, 按在相同干扰力下结构产生的最大振幅和振幅衰减的快慢程度来求动刚度; 对于自激振动, 按结构不产生自激振动的临界条件来求动刚度; 对于受迫振动, 按结构受激励力作用下的响应求其动刚度。

设单自由度系统受简谐激励力Fe的作用时, 其响应为Xe(-), 则两者之比的幅值, 即为单自由度系统动刚度的幅值, 其表达式为[7]

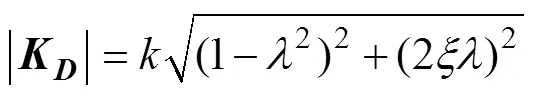
式中:为静刚度;=/ω为频率比;为激励频率;ω为系统固有频率;为阻尼比。

在实际的机械结构中, 理论上有无限多个自由度, 应该按照弹性体振动理论来分析动刚度的影响因素, 但是通用的方法是将整个结构体划分为若干个子结构, 把弹性体的振动简化为多自由度系统的振动来处理, 其以动刚度表达的运动方程为

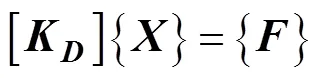
式中: {}为位移列阵; {}为激励力列阵; [K]为动刚度矩阵

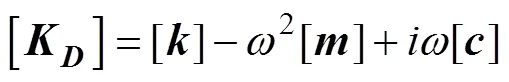
式中: []为系统质量矩阵; []为系统静刚度矩阵; []为系统阻尼矩阵;为激励频率。本文即采用上述方法, 用有限元法将系统划分为有限个单元进行受迫振动响应仿真计算, 从而计算动刚度。

2 隔振圈动刚度仿真计算

2.1 隔振圈有限元建模

首先使用UG建模软件对橡胶隔振圈的几何结构进行实体建模, 结构如图1所示。从图中可以看出, 隔振圈主要由3个部分组成: 内圈、橡胶体、外圈。内圈通过螺栓连接在发动机壳体上; 外圈则固定在鱼雷壳体上, 图中深色的即为橡胶, 它与内外圈粘接为一体结构。发动机产生振动通过橡胶的连接从内圈传递至外圈, 然后传递至壳体, 以辐射噪声的形式发散。

图1 隔振圈实体模型

根据此结构本文将隔振圈有限元网格模型按照实际模型划分为3个部分, 内外圈赋予金属材料钢的材料参数, 中间的橡胶体材料模型使用目前工程设计中广泛采用的Mooney-Rivlin模型。由硬度值通过下面公式可以得到隔振圈橡胶材料的弹性模量

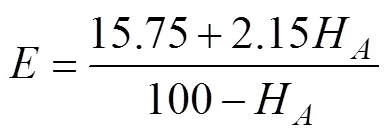
式中:为弹性模量;H为邵氏硬度。橡胶材料可以看成不可压缩, 则可以根据式(5)和式(6)得到Mooney-Rivlin橡胶材料模型的2个常系数

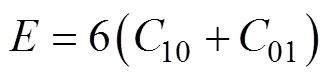
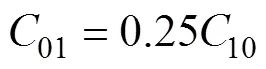
在此设定橡胶硬度60, 计算得10为0.482 5,01为0.120 6。

有限元模型中对隔振圈外圈表面节点进行了固定约束。根据实际情况, 隔振圈受力主要来自发动机通过螺栓的传导。因此, 在此将内圈螺栓孔周围节点与隔振圈圆心节点进行刚性连接, 激励则通过施加在圆心传导至螺栓孔进行施加。由于需要计算隔振圈的轴向、径向和轴向扭转刚度, 但这3个方向上的主要激励频率各不相同, 因此需要分别建立激励。激励基本形式为正弦激励, 幅值为1 000 N, 发动机转速为2 000 r/min。隔振圈轴向上主要受到高压燃气对活塞的冲击作用力及其反作用力, 因此激励频率应为转速的6倍; 径向上主要受力为旋转轴的离心力, 因此激励频率与转速相同; 轴向扭转方向主要受到凸轮对导槽平面的接触力引起的扭转力矩, 而接触力的变化频率是转速的两倍, 因此各方向上的激励函数如表1所示。

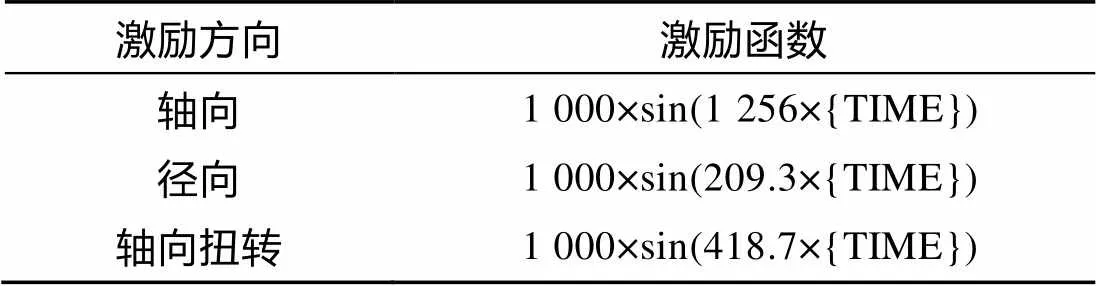
表1 隔振圈各方向激励函数表

整个有限元模型如图2所示, 共划分网格单元16 191个, 节点21 255个。其中橡胶单元6 426个, 节点11 281个。

图2 隔振圈有限元模型

2.2 仿真计算与结果分析

隔振圈在发动机运行时主要承受轴向力、径向力和轴向的扭矩, 因此本文将隔振器简化为这3个方向上的动刚度进行计算, 并与静刚度计算值作了比较分析。文中假设3个方向上刚度相互没有耦合。

使用ANSYS软件分别对隔振圈进行3个方向上施加正弦激励, 时间为0.06 s的瞬态仿真计算。由于本文主要研究隔振圈的动刚度, 不考虑其在真实情况下的响应情况, 因此没有在模型中施加阻尼。隔振圈的位移响应取隔振圈内圈螺栓连接区域的6个均布点位移值的平均值。动刚度计算则取位移平均值曲线的峰值与激励曲线的峰值的比值。单个节点的激励位移响应如图3所示,动刚度计算结果如表2所示。

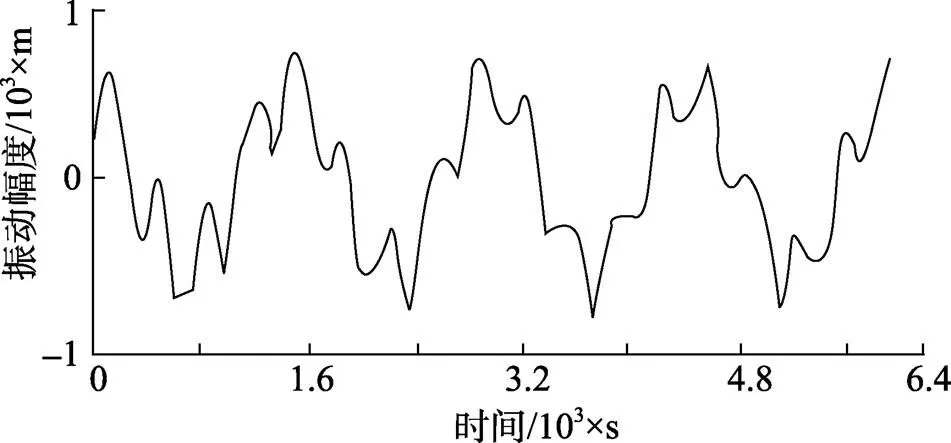
图3 单点激励响应曲线

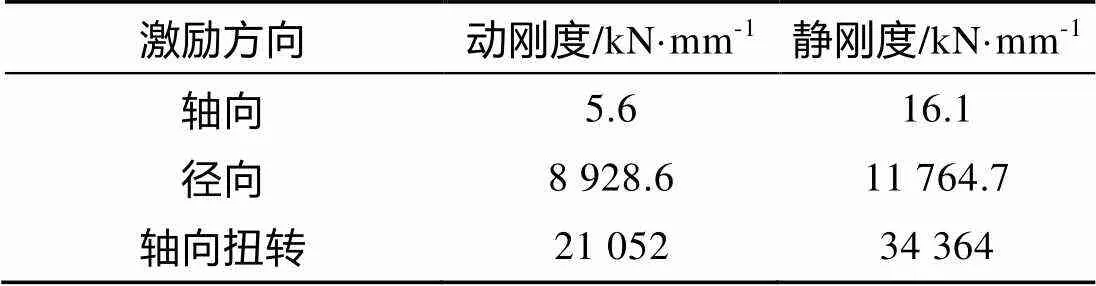
表2 隔振圈各方向动、静刚度计算值对照表

从图3中可以看出, 单点的振动响应基本按照激励的频率进行正弦变化, 但在变化的过程中曲线有所波动。曲线每个周期的峰值基本相同, 符合无阻尼激励响应的变化趋势。因此可以认为仿真计算符合实际情况。隔振圈各个方向动刚度值与静刚度值计算结果如表2所示。

从表中可以看出, 橡胶隔振圈轴向刚度远远小于径向刚度和轴向扭转刚度。其原因可能是因为轴向力造成了橡胶的剪切变形, 因而刚度很小。而径向力则是造成橡胶的压缩变形, 因而刚度较大。轴向扭转时虽然可能造成橡胶的剪切变形, 但从图1中可以发现, 隔振圈的结构使得橡胶在扭转方向上被内外钢圈的突出部分分割成多个几何独立的小块。在扭转变形时, 这些橡胶块在钢圈凸出部分的挤压下由剪切变形变为压缩变形, 因此扭转刚度变得很大。

另外从表中动、静刚度比较可以看出, 施加正弦激励后隔振圈的各个方向上动刚度较之静刚度都有不同程度减小, 其中轴向刚度减小幅度最大, 轴向扭转次之, 径向减少幅度最小。这与施加激励的频率正好成反比, 频率越高, 降幅越大。按照以往对橡胶材料动刚度的研究来看, 单独橡胶材料的动刚度与激励频率应成正比, 频率越高, 动刚度越大, 这点在对全部使用橡胶材料的隔振圈仿真计算中也得到了证明(见表3)。但在本文分析中两者却成反比, 分析其原因可能是因为将橡胶和金属圈作为一个整体进行分析时, 金属环在其中起的作用所造成的, 这一点有待于进一步分析。

表3 不同材料隔振圈轴向动、静刚度计算值对照表

3 结论

本文在理论分析的基础上提出了一种振动激励状态下计算橡胶减振器整体动刚度的方法, 并通过这种方法对橡胶隔振圈进行了动刚度计算。由此可以得出以下结论。

1) 将橡胶隔振圈作为一个整体进行有限元仿真计算, 可以有效地模拟动态激励下隔振圈整体的响应并计算出对应的动态刚度。此方法计算结果可以用于发动机振动性能的分析和优化以及隔振器的简化分析。

2) 隔振圈不同方向的动刚度不仅取决于橡胶的材料参数, 也取决于隔振圈的整体构造, 因此对隔振器进行动刚度分析不能仅仅对橡胶材料进行分析, 应将其作为一个整体进行计算。

3) 文中对隔振圈动刚度的计算是通过软件仿真得到, 如要应用到实际工作还需要得到试验的验证。

4) 文中总结的橡胶隔振圈动刚度变化趋势与单独橡胶材料变化趋势相反的结论, 其原理和真实性还需要得到进一步的研究分析和试验验证。

[1] 李锐, 陈伟民, 廖昌荣, 等. 发动机橡胶悬置特性的试验与建模研究[J]. 中国机械工程, 2009, 20(22): 2746- 2750．

Li Rui, Chen Wei-ming, Liao Chang-rong et al. Test and Modeling of Characteristics of an Engine Rubber Mount [J]. China Mechanical Engineering, 2009, 20(22): 2746- 2750.

[2] 李中付, 华宏星, 宋汉文, 等．用时域峰值法计算频率和阻尼[J]. 振动与冲击, 2001, 20(3): 5-7． Li Zhong-fu, Hua Hong-xing, Song Han-wen, et al. Identi- fication of Frequencies and Damping with Time Domain Peak Values[J]. Journal of Vibration and Shock, 2001, 20 (3): 5-7.

[3] Rao M D, Wirkner K J, Gruenberg S. Dynamic Characte- rization of Automotive Exhaust Isolators[J]. Journal of Automobile Engineering, 2004 , 218(8): 891-900.

[4] 姜洪源, 董春芳, 敖宏瑞, 等. 航空发动机用金属橡胶隔振器动静态性能的研究[J]．航空学报, 2004, 25(2): 140-142． Jiang Hong-yuan, Dong Chun-fang, Ao Hong-rui, et al. Research on Dynamic and Static Characteristics of Metal Rubber Isolator Used in Aero Engine[J]. Acta Aeronau- ticaet Astronautica Sinica, 2004, 25(2): 140-142.

[5] 范让林, 刘立, 吕振华, 等. 发动机隔振橡胶元件的有限元分析[J]. 内燃机学报, 2009, 27(2): 186-191． Fan Rang-lin, Liu Li, Lü Zhen-hua, et al. Finite Element Analysis of Engine Vibration Isolation Rubber Mount[J]. Transactions of CSICE, 2009, 27(2): 186-191.

[6] 刘龙, 刘高. 振动压路机橡胶减振器动刚度及黏性阻尼计算方法研究[J]. 建筑机械, 2009, 10(12): 81-83. Liu Long, Liu Gao. Research on the Calculation Method for Dynamic Stiffness and Viscous Damping of Rubber Isolators on Vibratory Roller[J]. Construction Machine, 2009, 10(12): 81-83.

[7] 王文斌. 机械振动和噪声[M]. 北京: 机械工业出版社, 2007．

Dynamic Stiffness Calculation Method for Rubber Ring Isolator

JIN Jing1, ZHANG Zhen-shan1, XIONG Xin2

(1. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China; 2. College of Electric and Information Engineering, Naval University of Engineering, Wuhan 430033, China)

Based on the conventional calculation method of dynamic stiffness for rubber ring isolator, a new calculation method is presented by simulating principal components of the isolator as a whole. Firstly, a finite element model of rubber ring isolator is established including metal and rubber parts. Then, sinusoidal excitations with different fre- quencies are exerted on isolator ring according to its actual force condition. As a result, dynamic stiffness in different direction is obtained by simulation. By comparing with static stiffness of isolator and dynamic stiffness of rubber, some variation rules of dynamic stiffness of the isolator are observed, which may benefit vibration analysis of engine and simplification of rubber ring isolator.

rubber ring isolator; dynamic stiffness; finite element model; simulation

TJ630.32; TH123

A

1673-1948(2012)02-0125-04

2011-05-19;

2011-09-16.

船舶工业国防科技预研基金项目(10106010302).

金晶(1981-), 男, 博士, 主要研究方向为机械装置设计与优化.

(责任编辑: 陈 曦)