基于风力机流场数值模拟的局部收敛分析研究

李 伟，孙凤芝，王金铭

(1.沈阳工业大学 理学院，辽宁 沈阳110870;2.大庆师范学院 数学科学学院，黑龙江 大庆163712)

0 引言

目前，国内对风力发电机组本身的气动特性分析研究主要体现在两个方面:一是叶片优化设计［1］;二是风力发电机系统控制、能量转换过程［2-3］。而对风力机气动流场模拟［4-9］主要是先对风轮机数学模型做一定程度的简化，再采用间接耦合方法［10-11］进行数值求解。由于间接耦合方法存在收敛性难以保证等缺点，因此采用直接耦合方法［12-14］数值求解风力机流场问题，具有重要的理论意义和应用价值。

本文的研究从叶片动态旋转入手，将风力机流场的求解区域看成圆柱体型区域，建立圆柱坐标系下的数学模型;将有限差分方法与牛顿法的结合应用到风力机流场数值模拟中，从理论上分析牛顿迭代格式局部收敛性，给出局部收敛性条件。

1 数学模型

1.1 基本控制方程

风力机流场是一个可压缩、有黏性的非定常流场，其控制方程属于流体力学方程。由于求解区域为圆柱体型区域，因此用圆柱坐标系(x，r，θ)较为方便。在圆柱坐标系下的控制方程可写为:

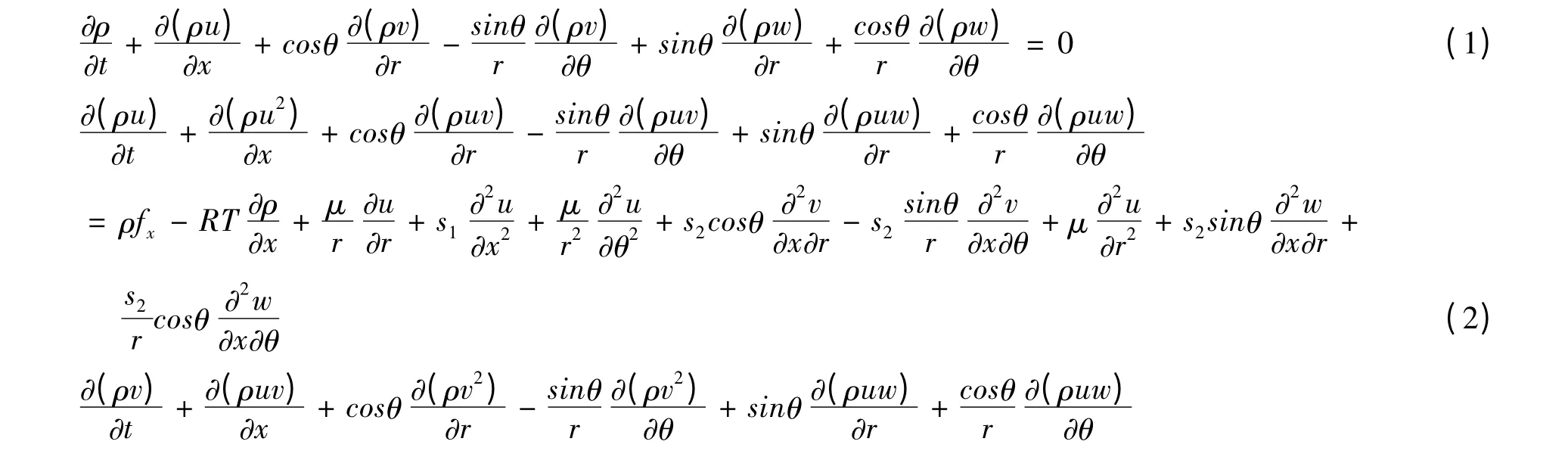
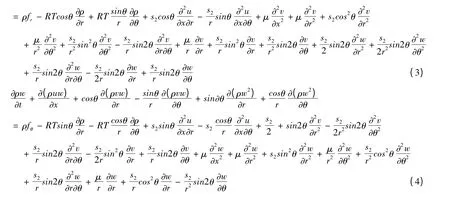
式中:u、v、w 分别为风速在x、r、θ 方向上的分量，ρ 为空气密度，R 为气体常数，T 是温度，s1= λ +2μ =4μ/3、s2= λ + μ = μ/3，λ 为流体的第二粘性系数，λ = -2μ/3，μ 为流体的动力粘度，fx= 0，fr= mg，fθ=3π/2。

1.2 定解条件、离散化格式及牛顿迭代格式

如图1所示的求解区域Ω 包括入口区域和出口区域两个部分，其中:边界Γ1为区域Ω 的外表面部分，Γ2为Ω1与Ω2的交界面。

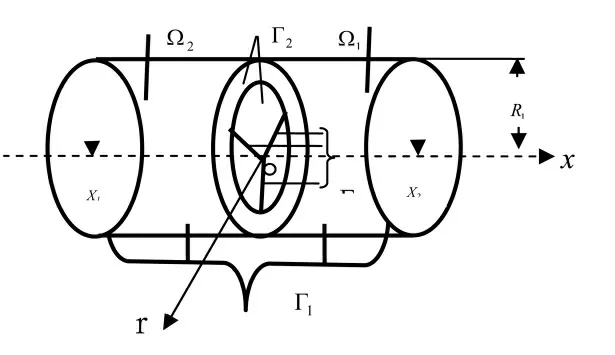
图1 求解区域

②边界条件:在Γ1上边界条件:v = v0，ρ = ρ0，在Γ2| Γ3上满足控制方程(1)～(4)，在Γ3满足边界条件:

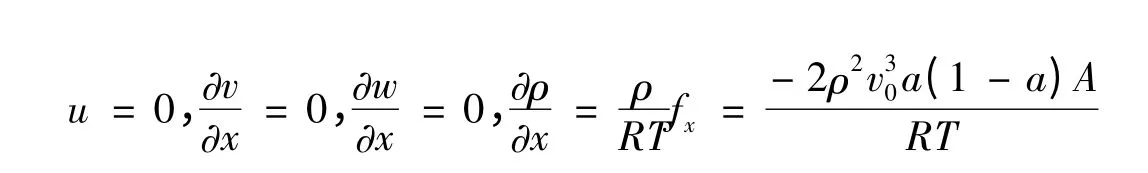
其中:v0为无穷远来流风速，ρ0为初始的空气密度，A 为风轮扫掠面积，a 为轴向诱导因子，ω 为角速度矢量的大小。可得由方程(1)～(4)、初始条件、边界条件组成的偏微分方程组的定解问题。

将如图1所示的求解区域Ω 进行如下剖分:

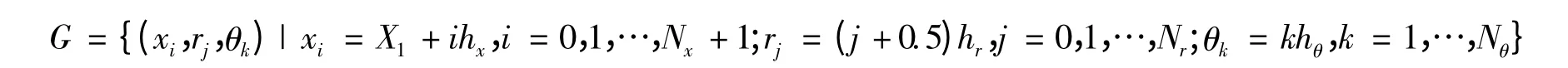
其中:hx=取时间步长为τ，时刻tm= mτ(m = 1，2，…)。

将方程(1)在时刻tm、在空间节点(xi，rj，θk)处对时间导数项采用向后差分、对空间导数项采用中心差分，得到方程(1)的两种情形的离散格式:

在x 轴上的空间节点(xi，r0，θk)处，控制方程(1)的离散格式如下:

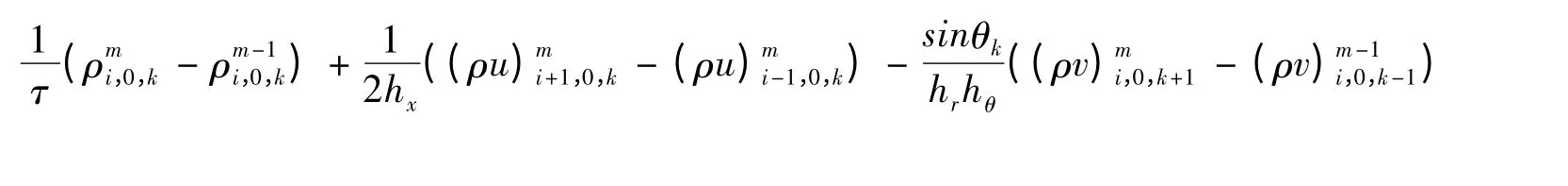
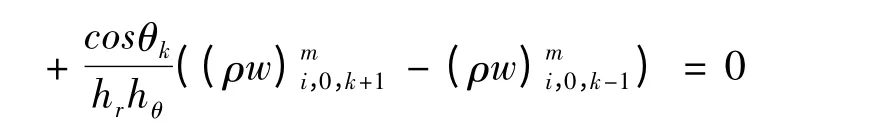
在任意空间节点(xi，r0，θk)，j ＞0 处，控制方程(1)的离散格式如下:

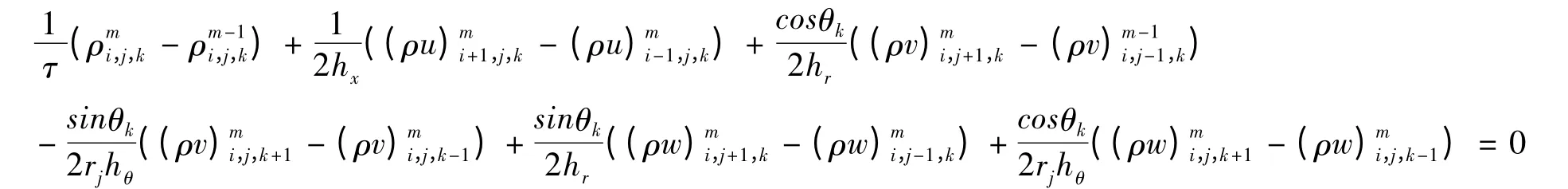
其中:X(m)=

利用牛顿迭代法求解式(5)，牛顿迭代格式为:

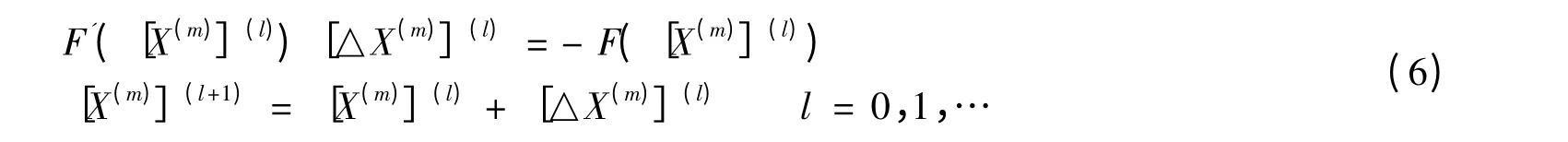
其中，l 为迭代步数，初始向量［X(m)］(0)取上一时间层的近似解向量Xm-1。

2 局部收敛分析

根据文献［13］，局部收敛分析是判断数值方法优劣的重要标准之一。下面的定理进一步说明了风力机流场数值模拟中的局部二阶收敛性。

定理1:若时间步长满足τ ≤min{τ1，τ2，τ3，}，则牛顿迭代格式(6)是局部二阶收敛的。其中:

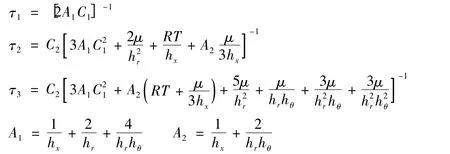
C1= ‖X*‖∞(X*是(5)的解)，C2表示密度ρ 在tm-1时刻求解区域Ω 内的最小值。

证明:F'(X(m))于X*的领域S(X*，δ)∈Ω 内连续G -可微，为了证明［F'(X(*))］-1存在，只需证明F'(X(*))为严格对角占优矩阵。

记F'(X*)= alq，F'(X*)中的第l = 4［(k -1)N1N2+ (j -1)N1+ (i -1)］+1 行非零元素是:

若要使F'(X*)中的第l 行严格对角占优，则只需

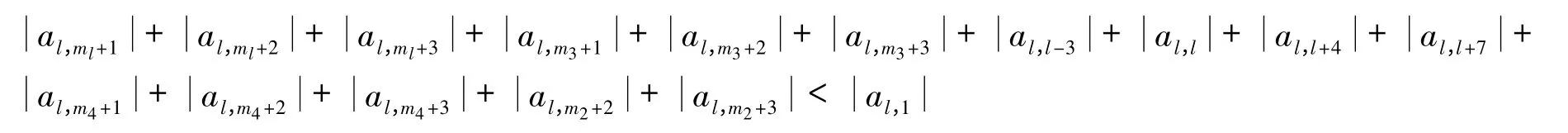
成立，即时间步长τ 满足τ ≤［2A1C1］-1= τ1。

类似的，可得到时间步长满足τ2时，F'(X*)中的第l + 1、l + 2 行严格对角占优成立;满足τ3时，F'(X*)中的第l + 3 行严格对角占优成立。因此，当τ ≤min{τ1，τ2，τ3}时，F'(X*)严格对角占优，［F'(X*)］-1存在。

对于∀h ∈Rn，h ≠0，F″(X*)hh 的第l 个分量是:

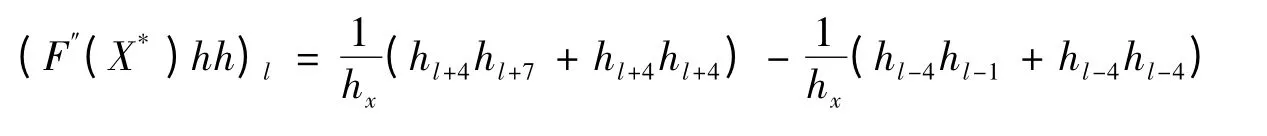
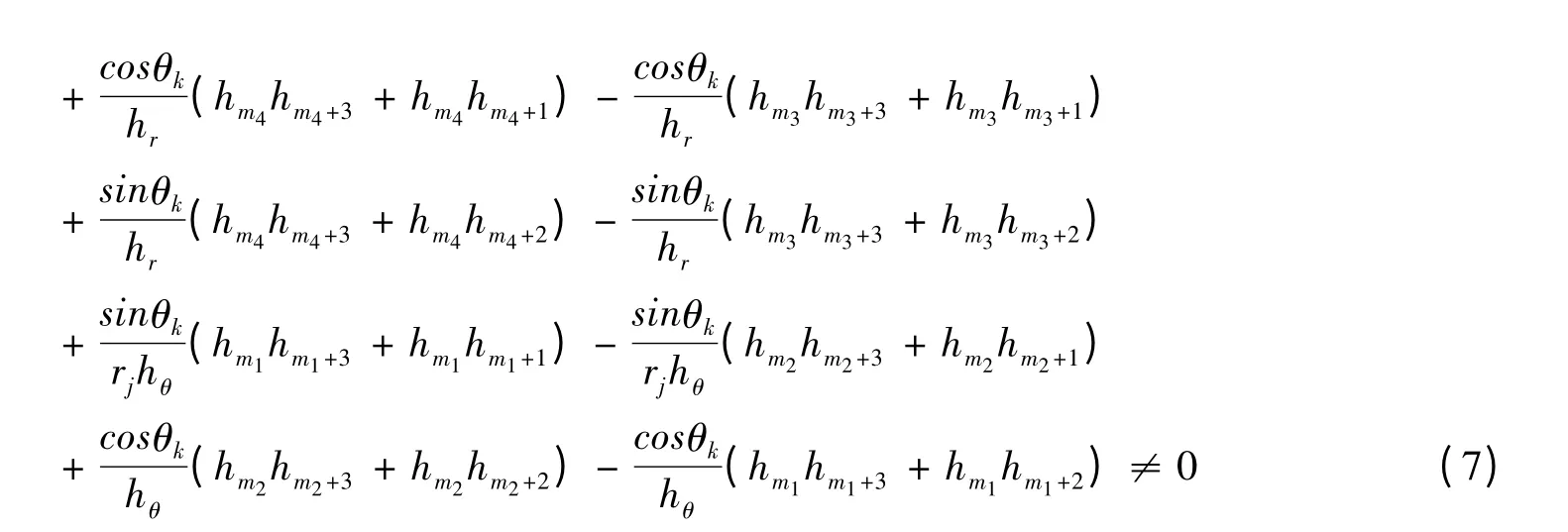
其中m1= l -4NxNr，m2= l +4NxNr，m3= l -4Nr，m4= l +4Nr。

同理可得到F″(X*)hh 中的第l +1、l +2、l +3 个分量是非零的，从而我们有:F″(X*)hh ≠0。综上，根据定理1 可知，牛顿迭代格式(7)是局部二阶收敛的。

3 结语

1)建立了圆柱坐标系下的风力机流场的数学模型，即非线性、非定常的偏微分方程组定解问题。

2)将有限差分方法与牛顿法的结合运用到数值求解中，以其中一个方程为例给出相应的有限差分方法离散化格式与牛顿法迭代格式。

3)分析迭代格式的局部收敛性，给出局部收敛条件。

［1］张立茹，汪建文，刘冬冬，等.水平轴风力机风轮子午面流场结构的实验研究［J］.太阳能学报，2011，32(3):323 -329.

［2］王果毅，董海涛.水平轴风力机的气动数值模拟［J］.太阳能，2008(3):30 -33.

［3］杨从新，宋显成.一种大型风力机叶片的气动优化设计方法［J］.空气动力学学报，2011，29(02):222 -225.

［4］何玉林，任海军，金鑫等.基于间接转矩控制的风电机组功率测控平台［J］.太阳能学报，2011，32(2):198 -203.

［5］Zhaoxue Cheng，Rennian Li.Criterion of aerodynamic performance of large scale offshore horizontal axis wind turbines［J］.Applied Mathematics and Mechanics，2010，31(1):13 -20.

［6］钱翼稷.空气动力学［M］.北京:北京航空航天大学出版社，2005:1 -53.

［7］Versteeg H K，Malalasekera W.An introduction to Computational Fluid Dynamics［M］.The Finite Volume Method.Longman Prentice Hall Press，1995:85 -54.

［8］张庆麟.风力机叶片三维气动性能的数值研究［J］.清华大学学报，2007，29(9):1172 -1174.

［9］葛永斌，田振夫，马红磊.三维泊松方程的高精度多重网格解法［J］.应用数学，2006，19(2):313 -318.

［10］傅作新，郑雄.弹性与弹塑性问题的有限元与边界元耦合解法［J］.计算数学，1993，10(4):375 -382.

［11］Hsu M H.Dynamic behaviour of wind turbine blades［J］.Proceedings of the Institution of Mechanical Engineers，Part C:Joumal of Mechanical Engineering Science，2008，222(8):1453 -1464.

［12］徐利治.几个敛速阶数较高的迭代程序和一个测定实根重数的方法［J］.数学学报，1962，12(4):331 -340.

［13］冯果忱.非线性方程组迭代解法［M］.上海:上海科学技术出版社，1989:112 -124.