简析高光谱图像解混技术及算法

成宝芝，张丽丽，齐 滨

(1.大庆师范学院 物理与电气信息工程学院，黑龙江 大庆163712;2.哈尔滨工程大学 信息与通信工程学院，哈尔滨150001)

1 概述

从20世纪60年代开始，随着信息技术、传感器技术和空间科学的进步，遥感技术得到了迅速的发展。到了20世纪80年代，由于成像光谱仪的研制成功和广泛应用，出现了具有“图谱合一”特性的新型遥感图像——高光谱图像。它的出现是遥感图像发展领域的一个飞跃，提高了人类认识世界和发现世界的能力。最近几年，国内外研究人员在高光谱遥感图像的地物分类、光谱解混和目标检测等方面进行了深入的研究，并取得了许多成果。

高光谱遥感信号是通过成像光谱仪获取的，成像光谱仪所记录的地表物质的反射信号是以像元为单位标记的。地表物质的光谱信号是由多个像元组成的。如果像元仅包含一种类型的地表物质，则称此像元为纯像元或者端元;若该像元包含两种以上地表物质，则称此像元为混合像元。混合像元的形成原因很复杂，归纳起来主要有两方面原因:1)传感器本身的原因和大气环境的影响;2)由于地表物质分布的复杂性，很容易发生不同特性的地物混合在一起的情况。例如沙土中混合了粘土。高光谱图像中混合像元的存在，使得传统的基于像元级高光谱图像的分类、压缩和目标检测等应用受到限制。所以，需要解决混合像元的分解问题［1］。图1给出了光谱解混的示意图。基于线性混合模型的高光谱解混主要包括两部分内容:端元提取和混合像元分解。

图1 光谱解混示意图

2 线性光谱混合模型

在分析高光谱含有的混合像元时，一般应用线性光谱混合模型［2］进行分析，线性混合模型的数学描述如图2所示［3-4］。在这种模型中，混合像元是由端元和对应的丰度线性混合组成，假设R 是波段为L 的高光谱混合像元图像，M 是一个L ×P 的光谱特征矩阵，列向量M =［m1，…，mp］为P 个端元向量，a =［a1，…，ap］T为每一列端元向量占有的丰度向量，线性混合模型可以写成如式(1)所示的矩阵形式:

其中，n 为一个L 维的噪声或者误差，P 个端元向量和对应的丰度都是未知量，本质上符合盲源信号分离问题。根据实际的高光谱图像端元光谱和丰度分布情况，对于光谱和它对应的丰度有两个约束条件:

①端元光谱及其丰度是非负的，即

②各个端元对应的丰度总和为1，即

基于上述的线性光谱混合模型，线性光谱解混过程由两个步骤组成，首先要进行端元提取，也就是把混合像元中含有的“纯”地物的光谱信息提取出来，也就是图1.10 中光谱信号矩阵M;第二步即混合像元分解，即用各端元的线性组合表示混合像元，也就是图1.10 中的丰度a 用端元矩阵M 来表示，实际上就是各端元在混合像元R 中所占的比例。下面分别对端元提取和混合像元分解进行综述。

图2 线性光谱混合模型图解

3 端元提取研究现状

由于遥感成像光谱仪器中使用的传感器空间分辨率受到技术条件的限制和观测的地物情况的复杂性，使得高光谱图像存在着混合像元的情况。如果把混合像元作为纯像元进行分类、目标探测等应用研究，结果会有很大的误差。这使高光谱解混问题成为近年来遥感领域的一个研究热点。而解混的第一步端元提取具有重要的作用，从20世纪90年代初开始，研究者就提出了端元提取的方法，在最近几年，端元提取的算法研究得到了迅速发展。这些算法基本上都集中在利用凸面几何学解决问题。典型的基于几何学的端元提取算法包括:Boardmand 等［5］提出的纯像元指数(Pixel Purity Index，PPI);Winter［6］提出的N -FINDR;Nascimento 等［7］提出的顶点成分分析(Vertex Component Analysis，VCA);Miao 等［8］提出的基于最小体积约束的非负矩阵(Minimum Volume Constrained Nonnegative Matrix Factorization，MVC -NMF)高光谱端元提取算法;Zhang 等［9］提出的基于蚁群优化算法的端元提取(Ant Colony Optimization Endmember Extraction，ACOEE)算法;Plaza 等［10］提出的基于自动形态学的端元提取算法(Automated Morphological Endmember Extraction，AMEE);Zortea 等［11］提出的空间预处理的端元提取(Spatial Preprocessing Endmember Extraction，SPEE)算法;罗文斐等［12］提出了零空间光谱投影(Null Space Spectral Projection，NSPP)的端元提取算法;Neville 等［13］提出的迭代误差分析(iterative error analysis，IEA)。表1示出了各个端元提取算法的性能，下面详细说明这些典型的端元提取算法。

3.1 纯像元指数算法

纯像元指数(PPI)算法来源于Boardman 利用凸面几何学的方法解决图像端元问题，随后其与Kruse和Green［5］一起发展和完善了PPI 端元提取算法。该算法首先采用最大噪声分量(Maximum Noise Fraction，MNF)变换对高光谱图像数据进行噪声白化和降维处理，使得每个波段的噪声都不相关，然后把数据降维到特征空间中。如图3所示，将光谱特征空间中的所有光谱点投影到单位向量上，端元就投影到向量得两侧，而混合像元则会投影到向量的中部［7］。因此，可以让高光谱图像在个随机的单位向量上投影，同时记录下高光谱图像中每个像元被投影到端点的次数，即为纯像元指数。当经过MNF 变换后的高光谱图像数据中的像元被投影到随机向量两端的次数越多时，此像元为纯像元的概率就越大。PPI 算法的缺点在于:从本质上来说，PPI 并不是一个完全意义上的端元提取算法，只是一个端元选择方法的指导;另外，PPI 是一种监督的端元处理算法，需要预先知道背景信息。

图3 纯像元索引法示意图

3.2 N-FINDER 算法

N-FINDER 算法利用了混合像元中端元分布呈现凸面单行体结构的特点［93］，如图4所示。N -FINDER 算法通过求取最大单行体的体积而得到各个端元，p 个端元e1，e2，…，ep的体积公式为

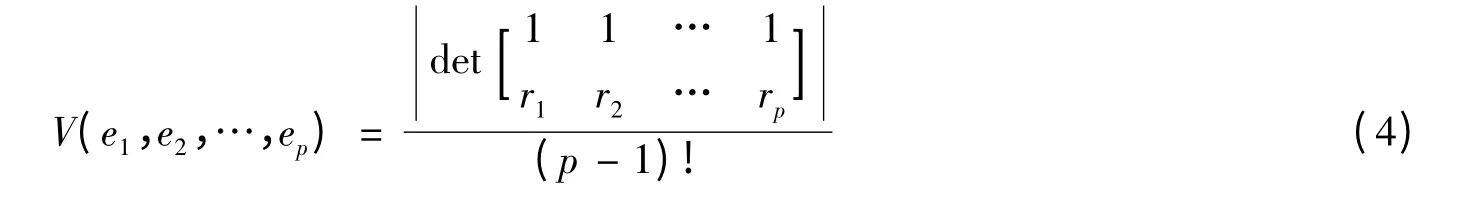
其中r1，r2，…，rp为e1，e2，…，ep降维后所对应的(p -1)维向量，目的是保证行列式为方阵，det［.］||表示行列式，为绝对值算子。

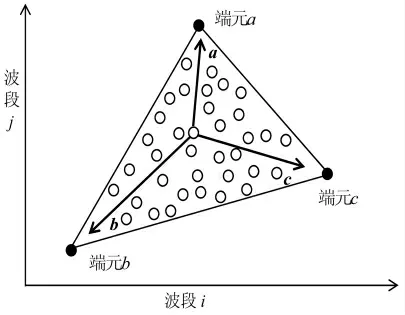
图4 N-FINDR 端元提取示意图

N-FINDER 算法的缺点是算法中需要的初始端元是随机产生的，初始端元值选的是否合适会影响算法的最终结果。另外，算法在单行体计算过程中需要计算体积，而体积计算的复杂度随着端元数目的增加呈现立方增加，导致计算时间过长计算速度降低，从而影响算法的性能。故王立国等［14］提出了距离计算等效于体积计算的基于等效原则的N - FINDER 改进算法，改善了传统N - FINDER 算法的端元提取性能。

3.3 顶点成分分析算法

顶点成分分析(VCA)算法是Nascimento 等在高光谱图像数据基于凸面单行体的几何结构的基础上，利用端元一定是单行体的顶点这样的几何事实。在先验知识很少的情况下，仅仅使用观测到的混合像元的数据来提取端元，是一种非监督情况下的快速端元提取的算法，图5是VCA 算法实现的原理图解。通过反复寻找正交向量并计算图像矩阵在正交向量上的投影距离逐一提取端元。Rk空间中寻找与p(p ≤k-1)个无关向量均正交的向量wp+1，可以利用施密特正交化法或正交子空间投影的方法［93，128］。施密特正交化过程首先需要找到一个与无关的向量u，之后计算下式

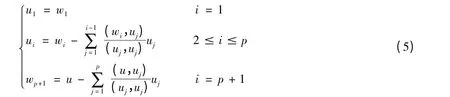
则所求得的wp+1与正交。

其中W#称为矩阵W 的广义逆矩阵(伪逆阵)，Ik为k 阶单位矩阵，W'为正交子空间投影矩阵。由于W'为阶方阵，且秩为k - p，即W' 中的列向量并非线性无关，其列向量的极大线性无关组构成W⊥的基底。但这并不影响对wp+1的计算，因为W' 列向量的任意线性组合均与正交，即

VCA 算法通过在已经确定的端元构成的子空间里反复正交投影高光谱数据，新的端元光谱对应的是投影的端点，当所有的端元点都被提取出来算法停止迭代。VCA 算法的缺点之一是它的初始端元要随机设定，影响算法的鲁棒性;另外，就是需要假定被解混的高光谱图像数据中一定含有纯像元［128］。

图5 顶点成分分析算法图解

3.4 MVC-NMF 算法

MVC-NMF 算法是Miao 等［8］在2007年提出的基于最小体积约束的非负矩阵分解的无监督的高光谱端元提取算法。如图6所示，该算法基于两个重要的高光谱图像数据特性:第一，光谱数据是非负的;第二，由端元构成的单行体是数据散布空间里所有可能存在的单行体中体积最小的。算法利用了非负矩阵分解方法快速收敛的特性，同时不需要假设存在纯像元。MVC-NMF 算法利用单形体的最小体积作为非负矩阵分解方法的约束条件，变成一个求解约束优化问题，即对于高光谱数据X(其波段数为L，端元数为c)有

其中，A 是光谱端元矩阵，S 是丰度向量矩阵，则利用非负矩阵得到

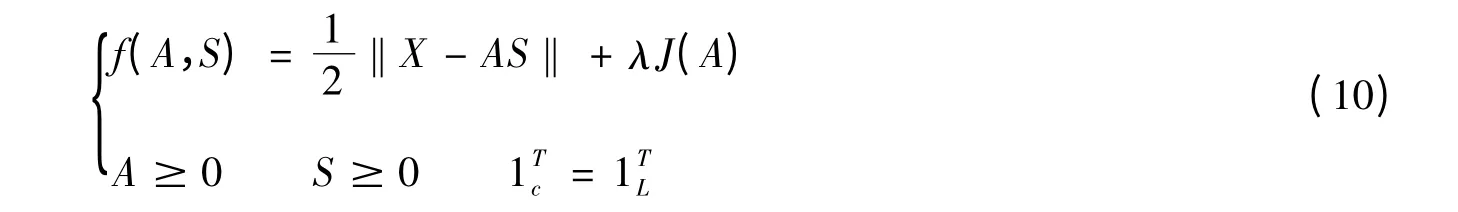
其中，1c(1L)是c(L)维列向量，J(A)是惩罚函数。为了求解上式，需要先确定J(A)。由单形体体积公式

对于式(10)的约束优化问题，基于最小单形体体积的目标函数为

U ∈Rl×(c-1)是X 经过PCA 方法变换后得到的c -1 个主成分分量构成的矩阵，得到

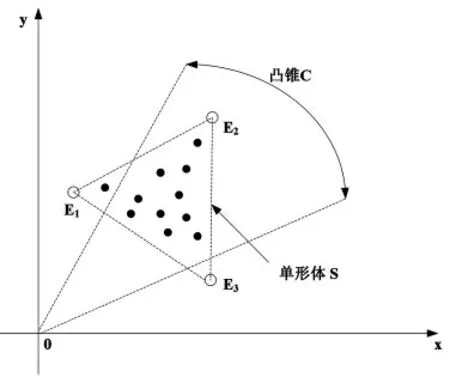
图6 MVC-NMF 算法中凸锥和单形体的几何图解

3.5 蚁群端元提取算法

基于蚁群(ACO)的端元提取算法是张兵等将智能算法ACO 引入端元提取问题中。该算法在基于线性光谱混合模型的基础上，利用直接和加权图的方法描述了两个像元间的关系。通过评估目标函数的实际意义，把端元提取问题转换为优化和构建可行解空间问题。基于ACO 的端元提取算法经过仿真验证，性能优于N-FINDER 和VCA 算法。

3.6 迭代误差分析算法

Neville 等提出的迭代误差分析(IEA)的端元提取算法，该算法在端元提取过程中，没有对原始高光谱图像进行降维或去冗余等预处理。在算法执行过程中，需要多次使用约束线性解混，要求得到的端元使得线性解混后误差最小。在算法开始执行时，它首先给定一个初始向量(所要处理的高光谱图像数据的平均光谱);对这个向量进行约束线性光谱解混，这样就得到误差图像［7］。其中误差最大(与初始向量相差较大)的像元作为第一个端元，接下来以第一个端元为初始向量进行第二次约束线性解混，得到误差图像中误差最大的像元为新的端元，重复以上步骤，直至在某种准则条件下求出图像中所有的端元［1］。IEA 算法具有良好的端元提取性能，在实际中得到广泛应用，特别是其基于迭代误差分析的思想，有许多研究者加以改进，提出了新的端元提取算法或者应用于其他高光谱图像处理技术中。

3.7 基于自动形态学的算法

Plaza 等提出的基于AMEE 的端元提取算法是一种非监督的自动算法。该算法充分利用了高光谱图像数据的光谱信息和像元在空间上的相关性，基于形态学，拓展了建立在二值图像上的腐蚀和膨胀算子，把这些算子用于高光谱图像中的端元提取。AMEE 算法的缺点在于很难有效区分光谱相似的不同端元，高光谱图像的结构元素的形状与图像尺寸直接会影响到算法性能.李娜等［15］对AMEE 算法进行改进，提出了基于形态学与正交子空间投影的端元提取方法，该算法利用扩展的形态学膨胀和腐蚀操作，先计算形态离心率指数，在此基础上，计算高光谱特性数据的端元数据集;然后，通过光谱角匹配方法提取不同类型的端元;最后通过向端元正交子空间投影，消除已经提取端元的影响。

3.8 基于空间预处理的算法

Zortea 等提出的基于空间预处理的端元提取算法，该算法提出了一个新的策略使空间信息和光谱信息相结合，在某一空间邻域内，一个空间导出的标量因素和光谱像元的相似性相关联，这个标量值用来权衡光谱信息的重要程度，这个光谱信息是和依据于空间上下文的像元相关联的。SPEE 有两个重要特性，一是算法没有改变原来的基于光谱的端元提取算法;二是算法增强了在空间分布同类区域的端元搜索能力。

3.9 基于零空间光谱投影的算法

罗文斐等提出的基于零空间光谱投影的端元提取算法，该算法在对线性光谱混合模型分析基础上，引入了高光谱图像数据经过零空间光谱投影后具有单形体的凸不变性的特点，通过设计各种端元度量和准则，制定不同的单次端元提取策略，实现了端元提取的目的。仿真实验表明，NSPP 端元提取算法是对基于子空间投影距离算法的延伸，是一种有效的端元提取算法。

表1 端元提取算法性能对照表

4 混合像元分解研究现状

基于线性混合模型，高光谱图像数据解混的第二步是混合像元分解，目前成熟的算法很多，本章介绍几个有代表性的混合像元分解算法。

4.1 最小二乘法

最小二乘法(Least Squares，LS)是式(1)在无约束条件下均方误差意义的最佳解，是目前应用最为广泛的算法。但是该解的表达式多次用到矩阵的乘积及求逆，特别是在端元数目较多的情况下，使得计算复杂度比较大。另外，由于没有附加任何约束条件，混合像元分解效果并不理想，会出现端元成分小于0 或者大于1 的情况。因此，Heinz 等［16］将式(2)和(3)作为式(1)的约束条件，提出了全约束的最小二乘法(Fully Constrained Least Squares Linear，FCLS)解决混合像元分解问题，同时还有对式(1)增加式(2)的非负约束的最小二乘法(Nonnegatively Constrained Least Squares，NCLS)，式(1)增加式(3)的丰度总和为1 约束的最小二乘法(Nonnegatively Constrained Least Squares，NCLS)，这些改进的LS 方法在一定条件下都改善了基本LS 算法的分解效果。

4.2 独立成分分析

独立成分分析((Independent Component Analysis，ICA)方法是Herault 和Jutten 等［17-19］于1986年提出的一种非常有效的盲信源分离技术，Lennon 等［20］在2001年把ICA 算法用于高光谱图像解混问题，Nascimento 等［21］在2005年进一步深入研究了ICA 在解混中的适用性问题。作为一种基于统计方法的混合像元分解算法，ICA 将观察到的数据进行某种线性分解，使其分解成统计独立的成分。但是，ICA 算法是以各种信号源的统计意义下的相互独立为前提条件，然而，高光谱图像数据各个组分并不能满足此要求。这就造成了基本ICA 算法的混合像元分解效果并不好，影响了ICA 算法在高光谱图像解混问题处理中的应用。上海复旦大学的夏威等［2］针对高光谱图像和ICA 算法的特点，在独立分量分析的目标函数中引入两个约束条件，即丰度非负约束与丰度和为1 这个线性混合模型的条件，改变了传统ICA 的独立性假设，发展了有约束的独立成分分析。实验证明，改进的ICA 算法对高光谱混合像元分解问题是有效的。

4.3 空间信息辅助下的混合像元分解

高光谱图像的采样使得地物影像离散化，但实际上自然地貌、地物、植被和水系等是自然连续的。由此得到，实际上每一个像元与其邻域的像元是具有相关性的，因此，对高光谱图像数据进行混合像元分解时，也应考虑像元在空间上的的相关性［1］。如图7(a)所示，一个9 格图，图中间的像元是要研究的混合像元，周围是其8 个相邻像元，图中虚线为各种地物的分界线，A，B，C，D 为4 种不同的纯地物，处于中间混合像元的8 个邻域像元中。由图7(b)可以看到，由于地物的连续性，中间的混合像元就是由其8 个邻域像元中的4 种不同地物A，B，C，D 组成的。

图7 混合像元空间示意图

把空间信息和光谱信息结合进行混合像元分解，近年来发展很快。如Mei 等［23］提出空间纯度的概念和光谱信息结合用于光谱混合分析;贾森等［24］提出的基于光谱和空间特性的高光谱解混方法。

4.4 投影寻踪

投影寻踪(Projection Pursuit，PP)方法是Friedman 等［25］提出的一种专门处理高维数据的降维方法。PP 算法的基本思想是把高维数据投影到低维可视子空间上，寻找能反映原高维数据结构或特征的投影(称为“令人感兴趣”的投影)，然后通过分析和研究投影数据以达到了解原数据的目的［1］。PP 方法能成功地克服高维数据的“维数祸根”所带来的严重困难，为采用一维统计方法解决高维问题开辟了途径。该方法的不足之处是计算复杂度高，耗费大量的计算时间。

其他还有一些混合像元分解算法，如Boardman 等4 提出的凸面几何学分析方法;Palmadesso 等［26］提出的滤波向量法;Chang 等［27］提出正交子空间投影(OSP)法;刘力帆等［28］提出的基于自组织映射和模糊隶属度的混合像元分解，本文不在赘述。

5 展望

随着高光谱图像技术的不断发展，对于图像中含有的混合像元问题的解决变得越来越重要［29］。高光谱图像解混算法的研究将在以下几个方面展开:

1)利用高光谱图像的混合像元中含有的端元具有稀疏性的特点，研究如何利用稀疏矩阵或者稀疏方法进行相应的解混算法研究;

2)现有的大部分算法都是基于高光谱图像中端元分布的几何特性进行混合像元分解的，并取得了较好的解混结果。随着人工智能算法的发展，把人工智能算法和端元的分布特性结合起来进行端元提取，是一个重要的研究方向;

3)将高光谱图像的光谱特性和空间特性结合起来，充分利用图像的光谱和空间特性进行解混算法研究;

4)未来一些新的信号和信息处理技术的出现和发展，如新的矩阵分解技术等，如何将他们引入到高光谱图像的解混问题的解决中，是未来的一个发展方向。

［1］童庆禧，张兵，郑兰芬.高光谱遥感——原理、技术与应用［M］.北京:高等教育出版社，2006:246 -247.

［2］N.Keshava.A survey of spectral unmixing algorithms［J］.Lincoln Lab.J.，2003，14(1):55 -78.

［3］S.Jia，Y.T.Qian.Constrained nonnegative matrix factorization for hyperspectral Unmixing［J］.IEEE transactions on geoscience and remote sensing，2009，47(1):161 -173.

［4］T.H.Chan，C.Y.Chi，Y.M.Huang.A convex analysis-based minimum-volume enclosing simplex algorithm for hyperspectral unmixing［J］.IEEE transactions on signal processsing，2009，57(11):4418 -4432.

［5］J.W.Boardman，F.A.Kruse，R.O.Green.Mapping target signatures via partial unmixing of AVIRIS data［C］.USA:in summaries of the VI JPL Airborne Earth Science Workshop，Pasadena，CA，1995:23 -26.

［6］M.E.Winter.N-finder:an algorithm for fast autonomous spectral endmember determination in hyperspectral data［C］.Image spectrometry V，Proc.SPIE 3753，1999:266 -277.

［7］J.M.P.Nascimento，J.M.B.Dias.Vertex component analysis:a fast algorithm to unmix hyperspectral data［J］.IEEE transactions on geoscience and remote sensing，2005，43(4):898 -910.

［8］L.D.MIAO，H.R.QI.Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization［J］.IEEE geoscience and remote sensing letters，2007，45(3):765 -777.

［9］B.Zhang，X.Sun，L.Gao，et al.Endmember extraction of hyperspectral remote sensing images based on the ant colony optimization (ACO)algorithm［J］.IEEE transactions on geoscience and remote sensing，2011，49(7):2635 -2646.

［10］A.Plaza，P.Martinez，R.Perez，et al.Spatial/spectral endmember extraction by multidimensional morphological operations［J］.IEEE trans.geosci.remote sens.，2002，40(9):2025 -2041.

［11］M.Zortea，A.Plaza.Spatial preprocessing for endmember extraction［J］.IEEE transactions on geoscience and remote sensing，2009，47(8):2679 -2693.

［12］罗文斐，钟亮，张兵.高光谱遥感图像端元提取的零空间光谱投影算法［J］.红外与毫米波学报，2010，29(4):307 -331.

［13］R.A.Neville，K.Staenz，T.Szeredi，et al.Automatie endmember extraetion from hyperspectral data for mineral exploration［C］.Canadian:in 21st canadian symposium on remote sensing，1999:21 -24.

［14］王立国，赵春晖，毕晓君.端元选择算法在波段选择中的应用［J］.吉林大学学报:工学版，2007，37(4):915 -919.

［15］李娜，赵慧洁.基于形态学与正交子空间投影的端元提取方法［J］.北京航空航天大学学报，2010，36(12):1457 -1460.

［16］D.C.Heinz，C.I.Chang.Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery［J］.IEEE transactions on geoscience and remote sensing，2001，39(3):529 -545.

［17］J.Herault，C.Jutten.space or time adaptive signal prcessing by neural network models［C］.USA:aip conference proceedings，1986，151:206-211.

［18］C.Jutten，J.Herault.Blind separation of sources I.an adaptive algorithm based on neuromimetic architecture［J］.Signal processing，1991，24(1):1 -10.

［19］P.Comon，C.Jutten，J.Herault Blind separation of sources.ii.problems statement［J］.Signal processing，1991，24(1):11 -20.

［20］M.Lennon，M.Mouchot，G.Mercier，et al.Spectral unmixing of hyperspectral images with the independent component analysis andwavelet packets［J］.in Proc.IGARSS，2001，6:2896 –2898.

［21］J.M.P.Nascimento，J.M.Bioucas Dias.Does independent component analysis play a role in unmixing hyperspectral data?［J］.IEEE transactions on geoscience and remote sensing，2005，43(1):175 -187.

［22］W.Xia，X.S.Liu，B.Wang.Independent component analysis for blind unmixing of hyperspectral imagery with additional constraints［J］.IEEE transactions on geoscience and remote sensing，2011，49(6):2165 -2179.

［23］S.H.Mei，M.Y.He，Z.Y.Wang.Spatial purity based endmember extraction for spectral mixture analysis［J］.IEEE transactions on geoscience and remote sensing，2010，48(9):3434 -3445.

［24］贾森，钱法涛，纪震，等.基于光谱和空间特性的高光谱解混方法［J］.深圳理工大学学报理工版，2009，26(3):262 -267.

［25］J.H.Friedman，J.W.Tukey.A projection pursuit algorithm for exploratory data analysis［J］.IEEE transactions on computers，1974，23:881-890.

［26］J.Bowles，P.Palmadesso，J.Antoniades.Use of filter vectors in hyperspectral data analysis［C］.San Diego:proceedings of the meeting of infrared spaceborne remote sensing III，1995:148 -157.

［27］C.I.Change.Further results on relationship between spectral unmixing and subspace projection［J］.IEEE transactions on geoscience and remote sensing，1998，36(3):1030 -1032.

［28］刘力帆，王斌，张立明.基于自组织映射和模糊隶属度的混合像元分解［J］.计算机辅助设计与图形学学报，2008，20(10):1307-1317.

［29］成宝芝，赵春晖，王玉磊.结合光谱解混的高光谱图像异常检测SVDD 算法［J］.应用科学学报，2012，30(1):82 -88.