基于改进的蚁群算法求解最优路径方法

李 云

(宿迁高等师范学校 计算机系，江苏 宿迁223800)

0 引言

实际工作中，由于供电线路的突发故障引起的停电，一方面会影响人们正常的工作与生活;另一方面，在某些情况下甚至可能产生意想不到的严重后果，如毁坏设备等。因此就要求工作人员能迅速的进行检修。为了保证检修的高效性，挑选最优的路径就相当关键。这就要求在故障产生后，监测系统能采集到故障信息并确定故障点，这样就可以使用智能算法把到故障点的所有路径里的最优的那一条找出来，可以使线路得到及时修复，有效的保证电力的恢复。最近，学者提出了很多算法来求解最优通路问题，具有代表性的有遗传算法、Dijkstra 算法与蚁群算法等。其中遗传算法本质上是随机优化，部分搜寻效果不佳，很有可能发生早熟收敛;Dijkstra 算法对于小规模最优路径问题求解效果还可以，但对于大规模的问题求解时，算法的性能会快速下降。

蚁群算法本质上用的是模拟进化的思想，既可以并行处理，又充分利用了正向反馈与启发搜索，所以该算法一经提出就获得了广泛的应用，比如说求解TSP 问题。但是基本蚂蚁算法也有不足之处，有时只能得到局部最优解。本文针对此问题进行了改进，并且把改进后的算法用于求解电力故障抢修问题中的最优通路。从仿真实验可以看出，算法改进后的性能得到明显改善。

1 基本蚁群算法模型和问题模型

用图来描述问题，节点数是n，V 是节点的集合。如果从S 点开始最终要到达T 点，蚂蚁最初都在S 点，第i 只蚂蚁在S 点起程，对接下来要到达的节点是按某种算法求得的，照此方式进行，最终到达目的地T，这样第i 只蚂蚁便可获得S 到T 的路径。在蚂蚁挑选某边后，会立即对此边的相关信息量进行更新，这就是部分更新方式。蚂蚁j 做类似的讨论，对每个蚂蚁都做这样的处理，便可获得当前循环里的最优解，只不过这个解是局部最优的，继续这样的循环，直到完成我们给定的次数，这时在找到的全部局部最优解里选一个最好的解就是整体最优解。其中，最关键的是蚂蚁决定将要通过的路径主要参考路上的信息量大小。tabuk(k =1，…，m)表示已走过的节点，根据进化过程对通路集合做动态调整。挑选下一个节点时，某条通路被选到的机率由它上的信息量和启发信息决定的，在t 时蚂蚁k 从i 到j 的概率为:

其中:allowedk= {V -tabuk}表示第k 只蚂蚁将有可能转向的全部节点，τij(t)表示t 时刻从i 到j 路上的信息量，α 是诱导因子，代表信息量通路的重要程度，β 是期望诱导因子，代表可见度的重要程度;ηij(t)是t 时刻的可见度，代表节点i 转到j 的期望度，其中，ηij(t)= 1/dij，dij是经过边(i，j)需要的时间。

在每个蚂蚁从起始点S 到结束点T 的搜索完成后，还需要更新残留信息，τij(t)是时刻t 时路径(i，j)的信息量的浓度，那么t +1 时刻该路径的信息量为:

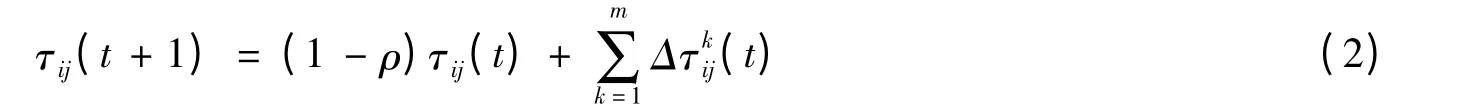
式中:ρ 显示信息素的挥发程度，ρ ∈［0，1)，则1 - ρ 是信息素的残留因子，指出残留的信息量相对的重要性;Δτij(t)是t 到t +1 时刻间路径(i，j)的信息量浓度增值，初始值Δτij(0)= 0;Δτkij(t)是第k 个蚂蚁在t 到t +1 时刻之间在边(i，j)上添加的信息量浓度。

实际问题的模型可以描述为:在供电系统产生故障后，需要找出一条到抢修点的最优通路。每条路的权值由相应的距离和路况来确定，这样我们便能将路线图用有向图(带权值)来描述。如果给定的有向图(有权值)G = (V，E)，集合V 中含有n 个节点，集合E 中含有h 条边，(i，j)代表E 里从点i 到节点j 的边，边(i，j)上的权值(非负)以wij来表示。如果S 表示V 起始点，T 表示V 的目的节点，则路径最优问题也就转换为:在G = (V，E)中搜索一条由S→T 的路径，要使通路上的权值达到最小。

2 改进后的蚁群算法

2.1 改进信息素区域与更新方式

因为受到正反馈的作用影响，基本蚁群算法在求解时经常出现局部最优解，这样后赶到的蚂蚁在寻找时选到局部最佳解的机率就很大，当循环数量逐渐变多时，局部最优解通路上的信息量会高出其余路径很多，那么就会让很大多数蚂蚁挑选这条路径，因此限制了该算法整体搜索性能，结果使算法陷入局部最优解。算法开始执行时，每一条通路的信息量均定为比较大的τmax，让信息素的更新不至于过度的影响路径上的信息素数量，使得蚂蚁的搜寻空间能更大些。为避免出现局部最优解(是部分路径上的信息素过多累积造成的)，可将通路上信息量设置两个临界值τmin、τmax，使信息素τ 的值如下:

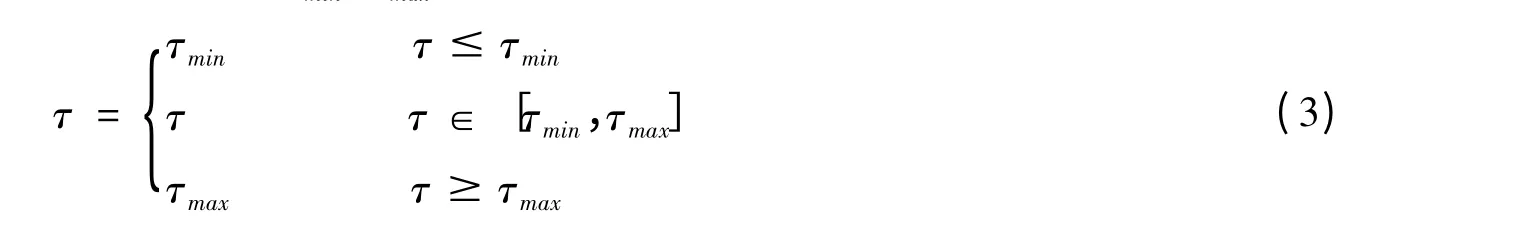
每当完成一次循环后，我们只更新某些特殊路径(已经算出最优解的那些蚂蚁所经之路)上的信息素，这样就可以做到使该算法沿着最优解的方向逐步收敛。

2.2 改进的部分搜索法

在过去的算法中，搜索的方向是依据路径上的信息量的多少来确定的。而在现实的寻径过程中，选择的路径不是无向的，而是有向的，比如正常的人从来就不会选择与自己的目的地相反的方向行驶。因此故障点和物资检修点的交叉点与中间节点构成［0，π］的角。而且现实生活里人们不可能提前预测故障产生的地方，因此若只存储角度的话，必须存(n - 1)2个相关的数据，这样就没有存节点的坐标节省空间。若i坐标用(ix，iy)表示，j 坐标用(jx，jy)表示，目标T 坐标用(Tx，Ty)表示，那么节点i 到j 的长度为:

同样方法可求得diT，djT。形成的∠ijT 可由下式求出:

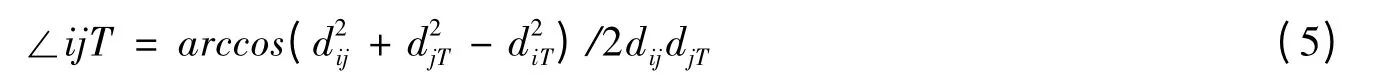
依此方法也能得到i 点、源点S 及目标点T 形成的∠SjT，其中η 反映节点转向的期望度，因此角度也是具有影响的因素因素之一，满足:

其中，μ 表示角度的权值。把ηij(t)代到式(1)中就可以求出pkij(t)。i，j 和T 形成的∠ijT 与所求出的一起决定应该如何挑选节点，如式(7)所示:

式中，γ 和λ 为两部分所占权重系数。

2.3 建立双向的搜索

基本的蚁群算法在求解TSP 等问题时容易陷入局部最优解，因为它是将所有的蚂蚁都置于起点，然后按照从起点到目标点的方向搜寻。基于上面存在这样的问题，我们可以假设一半蚂蚁从起点到目标点，另一半从目标点到起点，利用双向搜索减少蚂蚁彼此之间的影响，能够增加结果的多样化，从而达到全局的最优解。

3 算法仿真与实现

图1为某一地区的交通与电力路线图，其中颜色较深的矩形区域是某一物资检修点，故障点是深色地方所示。参照故障点与物资点的有关线路，可以用如下的带16 个顶点的有加权值的有向图(图2)来仿真，顶点1 作为起点，顶点16 是目标点，各边的路况和长度等权重信息如图2所示。相关参数设置为α =1，β = 5 ，m = 30，τmax= 10，τmin= 0.1，μ = 0.8，γ = 0.9，λ = 0.1/π，cycle = 50。

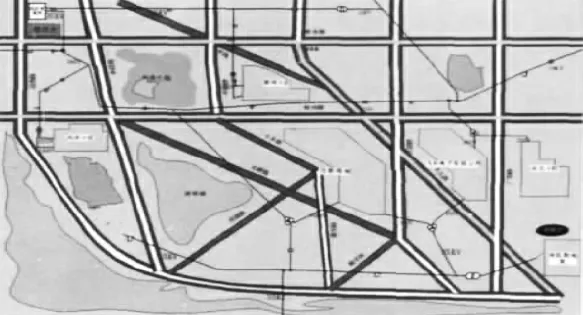
图1 路线的走向图

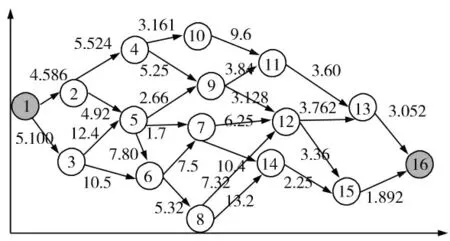
图2 带加权值的有向图

3.1 改进后的蚁群算法与基本算法的仿真对比

在给定的仿真条件下，下面的图3是未改进的蚁群算法求解顶点1 到达顶点16 的最佳路径的效果示意图，图4是用改进之后的算法求解这个问题的结果。

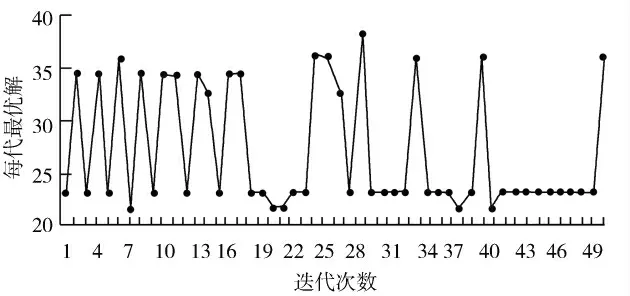
图3 用基本的蚁群算法进行仿真所得结果

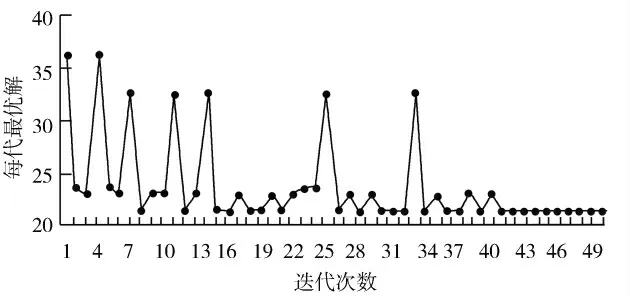
图4 用改进后的蚁群算法进行仿真所得结果

观察图3我们可以发现用基本蚂蚁算法寻求最优解时，50 代内的频率有很大波动，相比较而言要求得最优解不太容易，与此同时搜索还有一定盲目性，很容易导致最优解是局部的。从图4可以看出改进后算法求解初期有一定波动，可是迅速地往最优解方向收敛，迭代中期虽然偶有波动，最终还是完全收敛于整体最优解。

3.2 实验仿真的参数γ 与λ 的取值

用参数γ 表示角度在部分搜索选取节点时的权重，γ 的值在很大程度上影响节点的选取，在图5与图6中选取γ = 0.2，λ = 0.8/π 与γ = 0.8，λ = 0.2/π。

由两图对比情况可以发现，若角度权重的系数较大，用此算法执行部分搜索时，目标点与所在点的夹角越大越容易被被搜索到，从图2可以判断出:最终算法收敛于路径1→2→5→7→12→13→16，因为这条路径的角度相比较而言更占优势。此路径权重和为23.7，而且波动较大。但全局最优解应是1→2→5→9→12→13→16 这条路径，权值总和是21.55。把角度权值相应减小，算法就可以找出全局最优通路。

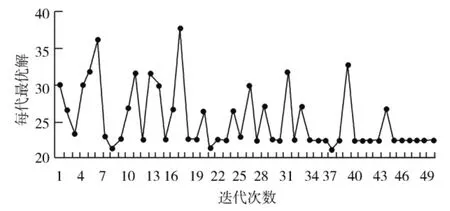
图5 角度权重系数较大

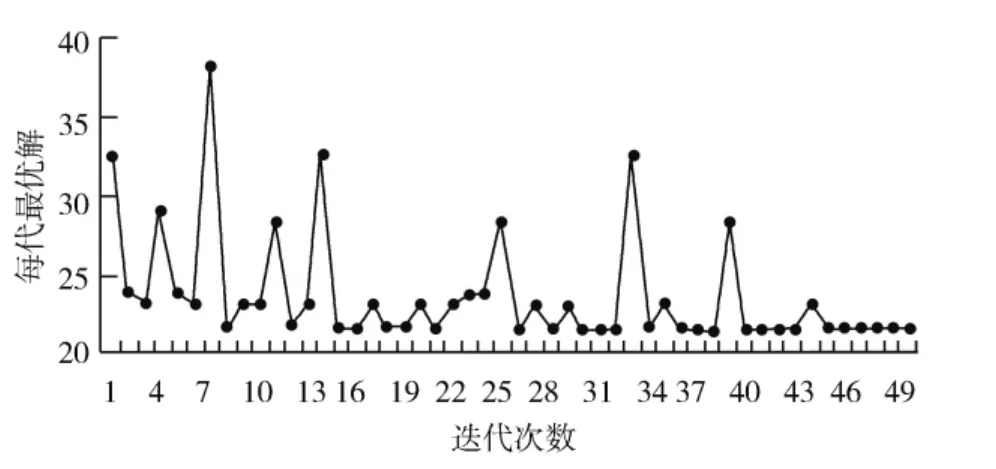
图6 角度权重系数较小

4 结语

基本的蚁群算法可能会很早就陷入局部最优解，在本文中，我们对此不足之处进行了改进。改进之一是引入“最大”、“最小”的方法;改进之二用角度配合信息量共同作用于部分搜索。把此法用于解决电路故障维修如何挑选最佳路径的现实问题，通过实验仿真表明改进后的算法明显提高了全局最优解的搜索能力。

［1］段海滨，王道波，朱家强，等，蚁群算法理论及应用研究的进展［J］.控制与决策，2004，19(12):1321 -1326，1340.

［2］Colony A，M.Dorigo ，Maniezzo V·Distributed Optimization by Ant Colonies［C］.France:Proc of 1st European Conf.Artificial life.pans，1991:134 -142.

［3］Dorigo M.Optimization，learning and natural algorithms［D］.Italy:ph.D.Thesis in politecnico imilano，1992.

［4］Dorigo M，Maniezzo V，Colorni A.Ant system:optimization by a colony of cooperating agents［J］.IEEE transaction on systems，man，and cybernetics-part B ，1996，26(1):29 -41.

［5］张纪会，徐新和，一种新的进化算法-蚁群算法［J］系统工程理论与实践，1999，19(3):84 -87.

［6］段海滨，王道波，于秀芬，等.基于云模型理论的蚁群算法改进研究［J］.哈尔滨工业大学学报，2005，37(1):115 -119.

［7］段海滨，蚁群算法原理及应用［M］.北京:科学出版社，2005.

［8］李士勇.蚁群算法及其应用［M］.哈尔滨:哈尔滨工业大学出版社，2004.

［9］秦岭.蚁群算法的改进及应用［D］.扬州:扬州大学硕士学位论文，2004.