求广义KdV方程孤立波解的一种迭代法

冯积社

(陇东学院 数学与统计学院，甘肃 庆阳745000)

0 引言

在孤立波解的研究领域内寻求非线性发展方程的解长期以来一直得到数学家和物理学家的关注。目前已得到基于计算机代数的许多方法，如双曲正切函数法［1］、齐次平衡法［2］、Jacobi 椭圆函数法［3］、辅助方程法［4，5］等。其中比较有效的方法是Adomian 分解法(ADM)［6］，尽管一般情况下得到的是近似解，但有时也可以得到精确解［7］。此外这种方法比标准的数值方法更具优势，因为不需要进行离散化从而不用修正误差，并且不需要大量的计算机内存和运算能力，因此对于许多非线性方程，ADM 能够提供精度非常高的数值解且收敛非常快［8］。

标准的ADM 方法需要显式求Adomian 多项式［6］，文献［9 -11］用ADM 求解KdV 和几类推广的KdV方程;文献［12］对标准的ADM 方法作了改进，得到了不用显式求Adomian 多项式的一种新的ADM 方法。本文利用文献［12］的方法求解一类广义的KdV 方程的孤立波解，借助Maple 求得了一类广义KdV 方程的孤立波解的高精度的近似解。

1 广义KdV 方程

本文中的广义KdV 方程是指［10］

其中p 为正整数，取1，2，3…，ε 和μ 是正常数。初值条件为u(x，0)=f(x);边值条件为:当|x|→+∞时，u，u″→0。设c 表示波沿着x 轴的正方向传播的速度，进行行波变换

则(1)可变为常微分方程

对(3)两边积分，并注意其边值条件，从而得到

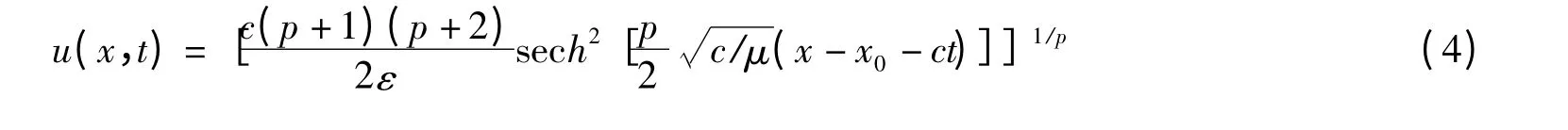
2 标准的ADM 方法及改进的ADM 方法

对于方程

其中L 表示待求函数u(x，t)关于t 是最高阶导数，R 是除L 外的其余线性运算项，F(u)是非线性运算项，g(t)关于时间的函数。若L 的逆运算L-1可表示为

对(5)两边进行运算，得

其中f0是满足初值和边值条件的齐次方程Lu=0 的解。

标准的AMD 方法是假设待求函数u(x，t)为无穷级数和的形式

非线性F(u)项可分解为所谓的Adomian 多项式级数和的形式

其中An是基于u0，u1，…，un而求得，具体为

改进的ADM［12］定义了一种新的Adomian 多项式

其中sn=u0+u1+Λ+un-1。这样由(11)，有

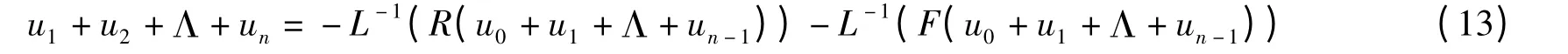
由此得到算法:

3 广义KdV 方程的求解

下面分别对于(1)中p=1，2，3，利用上面介绍的改进ADM 求出其孤立波解。

1)当p=1 时，取c=1.3，ε= -6，μ=1，若取其初值条件为此时(1)为

两边关于t 积分，得

与(5)对应的，这里R(u)=uxxx，F(u)=uux，g(t)=0，根据上述改进的ADM，有

从而可得到方程(12)的精确解

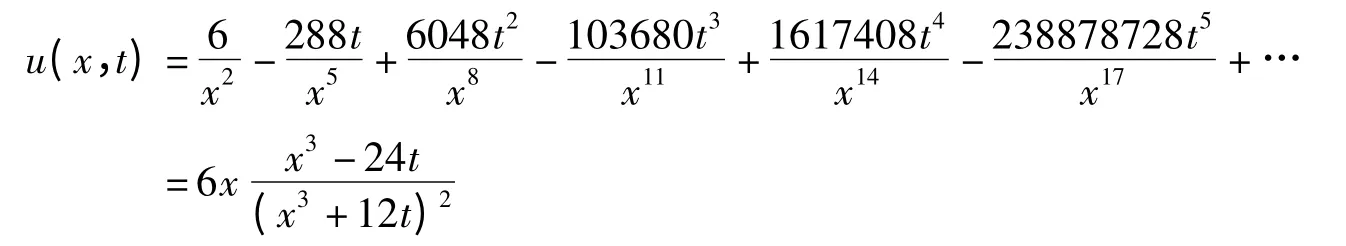
这与文献［9 -11］的结果是一致的，注意在文献［11］中有笔误。

2)当p=2 时，取c=1，ε=6，μ=1，若取其初值条件为u(x，0)=seeh(x)［10］，此时(1)为

可变形为

与(5)相对应，这里R(u)=uxxx，F(u)=u2ux，g(t)=0。根据上述改进的ADM，采用Maple 软件可以求到

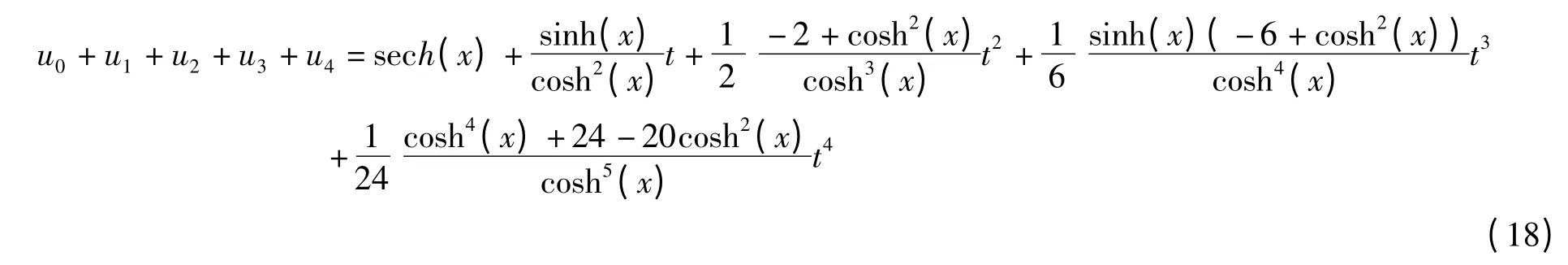
这虽然是近似解，但已经跟其精确解比较，近似的程序相当好了。这一点通过图1与图2可以看到。

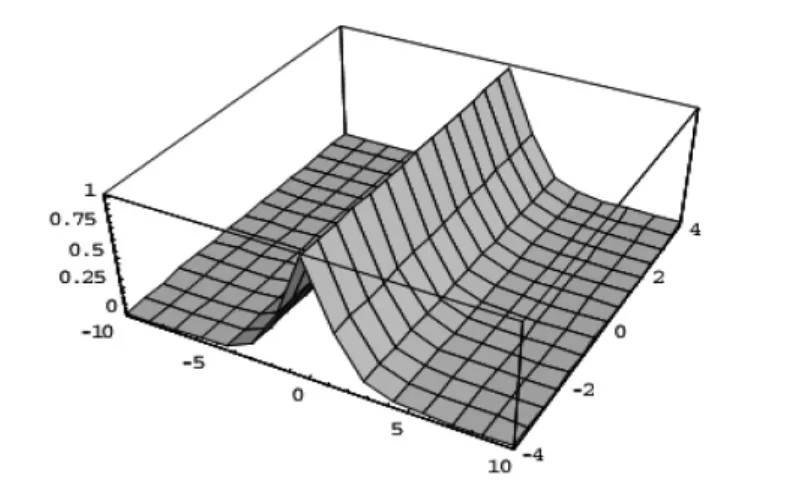
图1 精确解sech(x-t)的图像

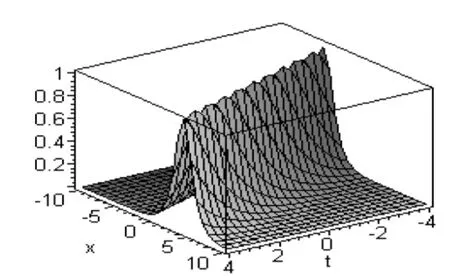
图2 近似解公式(18)的图像

3)当p=3 时，取c=0.6，ε=6，μ=1。若取初值，此时(1)为

与(5)对应的，这里R(u)=uxxx，F(u)=u3ux，g(t)=0。由上述改进的ADM，利用Maple 软件可以求得

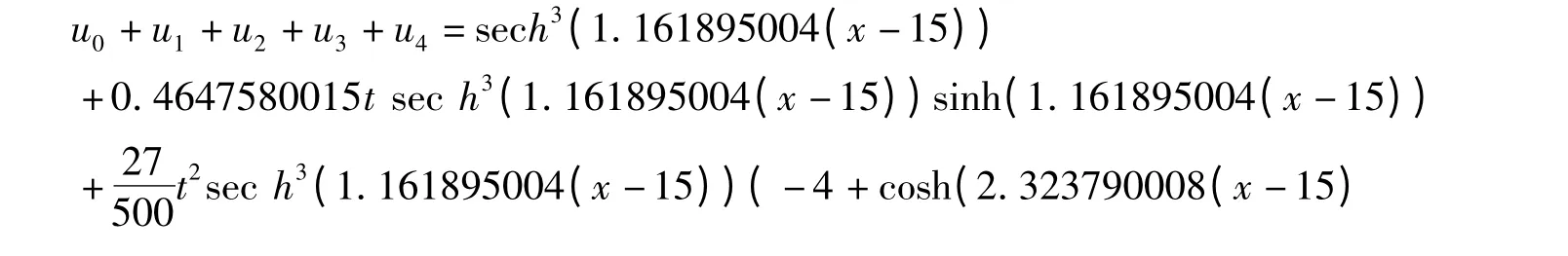
可以通过图3精确解sech(x -t)的图像和图4近似解公式(20)的图像的比较看出，近似的程度已相当好了。

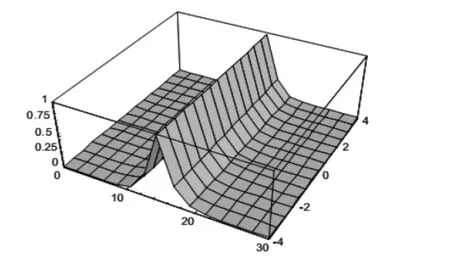
图3 精确解sech(x-t)的图像

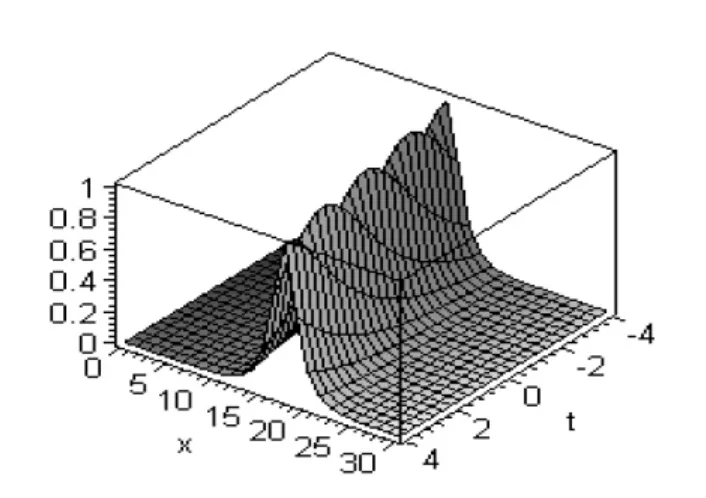
图4 近似解公式(20)的图像

4 结语

本文利用改进的Adomian 分解法，讨论了一类广义KdV 方程的孤立波解，最后通过计算机代数软件Maple 求得了精确度比较高的近似解。

［1］V.E.Zakharov，A.B.Shabat.Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media［J］.Sov.Phys.JETP，1972，34(1):62 -69.

［2］Pushkarov D.，Tanev S..Bright and Dark Solitary Wave Propagation and Bistability in the Anomalous Dispersion Region of Optical Waveguides with Third-and Fifth-order Nonlinearities［J］.Opt Communications，1996，124(2):354 -364.

［3］Tanev S，Pusharov D I .Solitary wave propagation and bistability in the normal dispersion region of highly nonlinear optical fibres and waveguides［J］.Optics Communications，1997，141(2):322 -328.

［4］套格图桑，斯仁道尔吉.构造非线性发展方程精确解的一种方法［J］.物理学报，2006，55(12):6214 -6221.

［5］Sirendaoreji，Sun Jiong.Auxiliary equation method for solving nonlinear partial differential equations［J］.Phys.Lett.A.，2002，309(1):387-396.

［6］G.Adomian.A review of the decomposition method in applied mathematics［J］.J.Math.Anal.Appl.，1988，135(4):501 -544.

［7］Wazwaz A.M.Necessary conditions for the appearance of noise terms in higher-dimensional spaces［J］.Appl.Math.Comput .，2002，130(2-3):415 –424.

［8］D.Lesnic.Convergence of Adomian＇s decomposition method:periodic temperatures［J］.Comp Math Appl.，2002，44(1):13 -24.

［9］A.M.Wazwaz.Construction of solitary wave solution and rational solutions for the KdV equation by ADM［J］.Chaos，Solution and fractals.，2001，12(6):2283 -2293.

［10］Hassan N.A Ismail，Kamal R Raslan，Ghada S.E Salem.Solitary wave solutions for the general KDV equation by Adomian decomposition method［J］.Applied Mathematics and Computation，2004，154(1):17 -29.

［11］Kaya，Mohammed，Aassila.An application for a generalized KdV equation by the decomposition method［J］.Phys.Lett.A ，2002，299 (1):201 -206.

［12］S.H.Behiry，H.Hashish，I.L.El-Kalla.A new algorithm for the decomposition solution of nonlinear differential equations［J］.Computers＆ Mathematics With Applications，2007，54(4):459 -466.