一类“00”型未定式极限的简单求法
李 娟
(天津河东区职工大学,天津 300171)
“00”型未定式极限一般在求幂指函数的极限时产生,通常采用换底方法,即limf(x)g(x)=elimg(x)lnf(x)转化为“0·!”,再进一步转化为“”型极限,利用罗必达法则求解。但是,当极限式子中的f(x)、F(x)比较复杂,或者其求导运算比较麻烦时,应用罗必达法则就会遇到很多不便。为解决这个问题本文给出一个新的方法,可以使计算或证明过程得以简化。
为此,先提出如下命题:
命题 设α、β、α′、β′均为同一自变量变化趋势下无穷小,且α>0,α′>0,α~α′,β~β′。如果极限limα′β′存在,则limαβ存在,且limα′β′=limαβ
证明 设y=αβ,取对数,有lny=βlnα,
于是limlny=lim(βlnα)
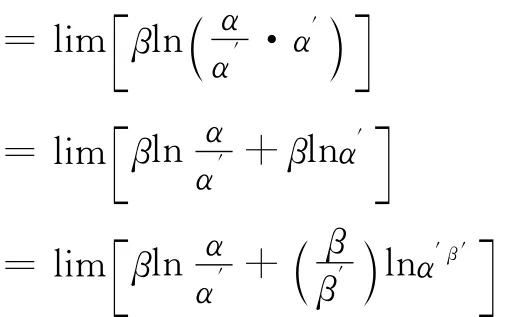
由题设limβ=0,lim=1,lim=1
lim(lnα′β′)=ln(limα′β′)存在
故limlny= (limβ)(lim)+ (lim)[lim(lnα′β′)]
=0·1+1·ln(limα′β′)
=ln(limα′β′)
则limy=limelny=elim(lny)=eln(limα′β′)=limα′β′证毕通过举例,来看此命题的应用及其优点。
解法一 设y= (sinx)tanx,取对数,有lny=tanx·(lnsinx)


解法二 当x→0+时,sinx>0,tanx>0
且sinx~x,tanx~x
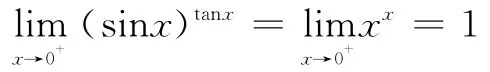

解法二 当x→+!时,-arctanx>0且
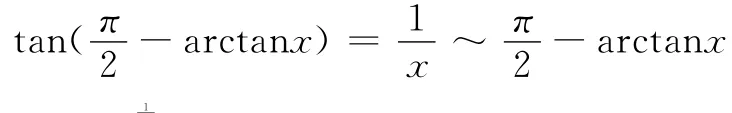
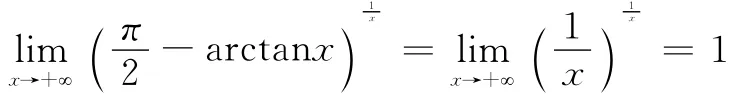
解法一 设y= (cotx)arcsinx,取对数,有lny=arcsinx·lncotx
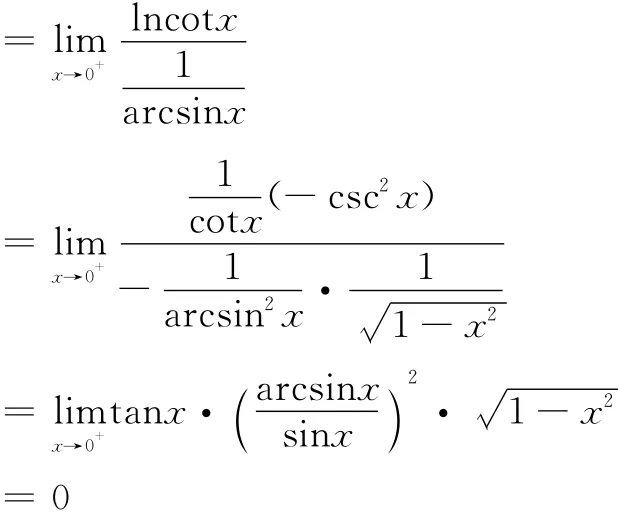
解法二 当x→0+时,tanx>0,arcsinx>0,
且tanx~x,arcsinx~x,
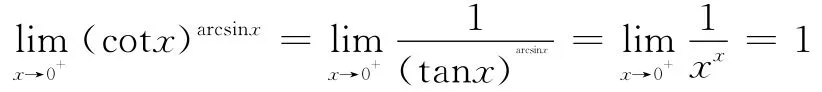
我们知道,当x→0+时,x,sinx,arcsinx,tanx,arctanx,ln(1+x)均大于0,且是彼此等价的无穷小量。因此,在求幂指函数αβ的极限时,如果出现它们,均可用x代替,从而使计算大大简化。
[1]刘玉縺编.数学分析[M].北京:高等教育出版社,1985.
[2]盛祥耀编.高等数学[M].北京:高等教育出版社,1987.

