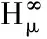从Bergman空间到Dirichlet空间的广义Cesàro算子*
孟 一 梅
(杭州电子科技大学 理学院, 浙江 杭州 310018)
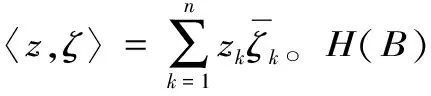
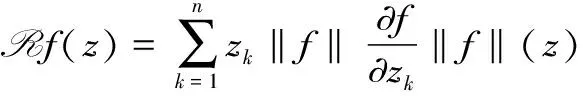
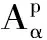
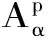
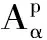
本文中,所有出现的p,q,α,β均满足0
1 Tg的有界性和紧性
引理 2.1 设p≤q,g∈H(B), 则
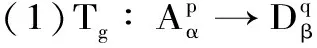
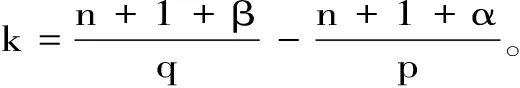
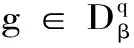
定理 2.1 设q 证明:(B)⟹(A) 是显然的; (A)⟹(C)的证明: 首先,当f,g∈H(B)时,可直接计算得出: R(Tgf)(z)=f(z)Rg(z)。 其中dμ(z)=|Rg(z)|q(1-|z|2)βdV(z)。 由文献[4]中定理4可得: (1) 因此,对任意ɛ>0,存在δ>0使得: (2) 定理 3.1 设g∈H(B),则当p≤q时, (3) (4) 证明: 则当Q∈K时,由Tgfζj(0)=0可得: 由本性模的定义和上面的估计式,有 (5) (6) (7) (8) 其中ck是给定的与n和k有关的常数。设0 (9) (10) 由引理2.1可知Tgρ是紧的。从而由(8)、(9)和(10)式可得: 故由文献[7](P15)中定理1.12得: (11) 由(5) 、(6)和 (11)式即可得出估计式(3)。 (12) (13) 由(12) 和 (13)可得估计式(5)。证毕。 本文在文献[1-6]的基础上进一步探讨了复合算子Tg的有界性和紧性,完善了文献[6]的结论,并给出了Tg本性模的估计式,在多复变函数空间算子研究领域具有一定的理论价值和应用前景。 参考文献: [1] Z. J. Hu. Extended Cesàro operators on the Bloch space in the unit ball of Cn[J]. Acta. Math. Sci., 2003, 23B(4): 561-566. [2] T. Hosokawa. The essential norm of a weighted composition operator from the Bloch space to H∞[J]. Bull. Aust. Math. Soc., 2009, 79(3): 487-497. [4] Z. J. Hu. Extended Cesàro operators on Bergman spaces[J]. J. Math.Anal.Appl.,2004,296:435-454. [5] 张学军.Cn中Dirichlet型空间和Bloch型空间上的加权Cesàro算子[J].数学年刊,2005,26A(1):139-150. [6] 易奎英,刘竟成,Bergman空间到Dirichlet空间的Cesàro算子,湖南工业大学学报[J].2008(3):24-26. [7] K. H.Zhu. Space of Holomorphic Functions in the Unit Ball[M].New York,Grad. Texts in Math.Springer-Verlag, 2005:226.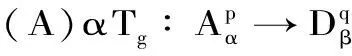
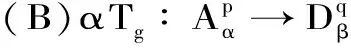
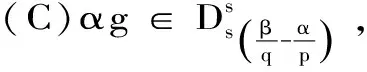


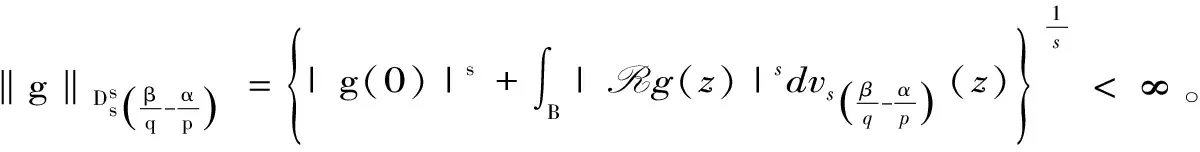
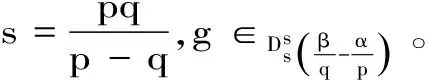
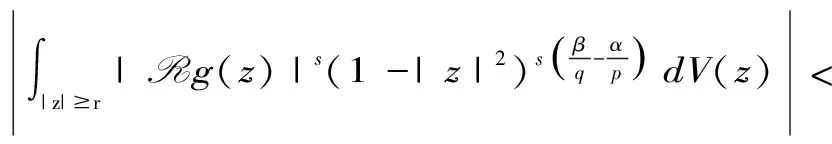
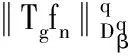
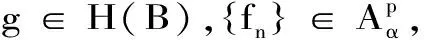
2 Tg的本性模
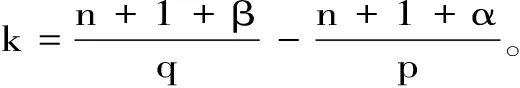

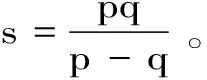
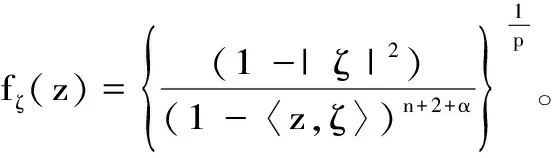
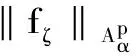
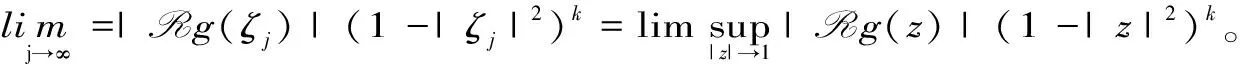
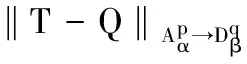
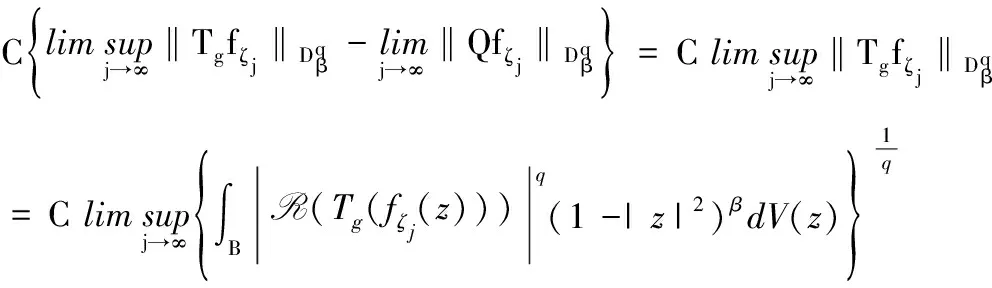
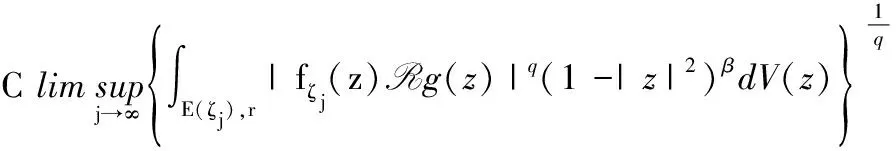
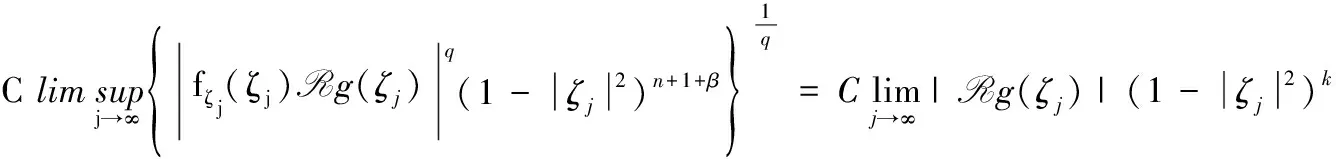
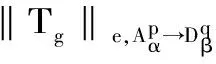
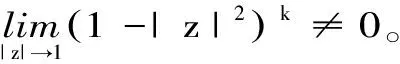
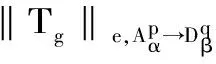
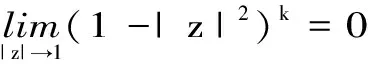
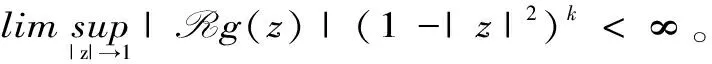
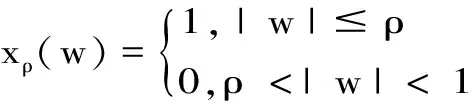
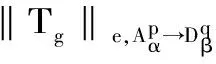
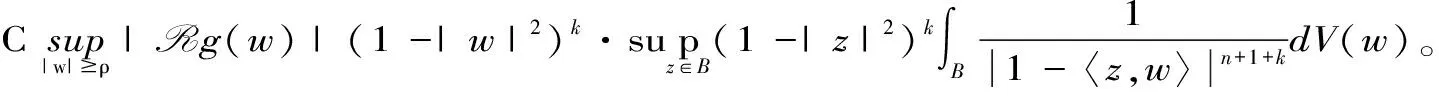
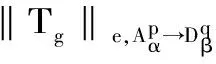
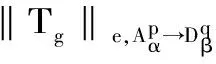
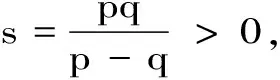
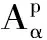
3 结 语