井用泵水力模型设计及试验研究

赵秋霞

（太原理工大学 力学学院，太原030024）

离心泵是量大面广的通用机械，在国民经济各部门发挥着重要作用。为了设计高效节能的离心泵，国内外专家学者进行了大量探索研究，但至今仍没有成熟的理论和设计方法，水泵的水力模型设计依然是采用相似设计原理并在大量统计资料基础上建立的经验公式和速度系数法，泵性能的好坏也无法通过理论计算得出，只能通过实验验证。井用泵属离心泵范畴，但井用泵机组最大外径受到井径限制，所以水力模型设计不能完全套用离心泵设计方法，有其独特性。因此我们针对井用泵特点采取了理论设计和实验相结合的方法，进行了大量设计研究、实验分析，提出了井用泵水力模型主要几何参数的选取原则和选择范围。并完成了适用多种井径、多种型号的井用泵水力模型设计和样机试制工作。

1 叶轮进口参数选取与实验分析

1.1 叶轮轴面投影图

井用泵的核心工作部件是叶轮，叶轮的几何形状是由轴面投影图和平面投影图共同表示的。在初步确定叶轮几何参数后，首先要绘制轴面投影图，然后再用保角变换法或扭曲三角形法绘制平面投影图。轴面投影图绘制往往是依靠经验绘制的，有很大的任意性，我们采取了与传统离心泵不同的方法，将叶轮后盖板设计成倾斜的，接近混流泵形状，目的是加大叶轮做功能力并使之与导流壳合理匹配。如200QJ32泵叶轮轴面投影图采用了两种方案，一种后盖板倾斜度较大，（取θ＝25°），另一种较小（取θ＝13°）。试验表明第一种方案效果较好。图1为两种叶轮轴面投影图比较。

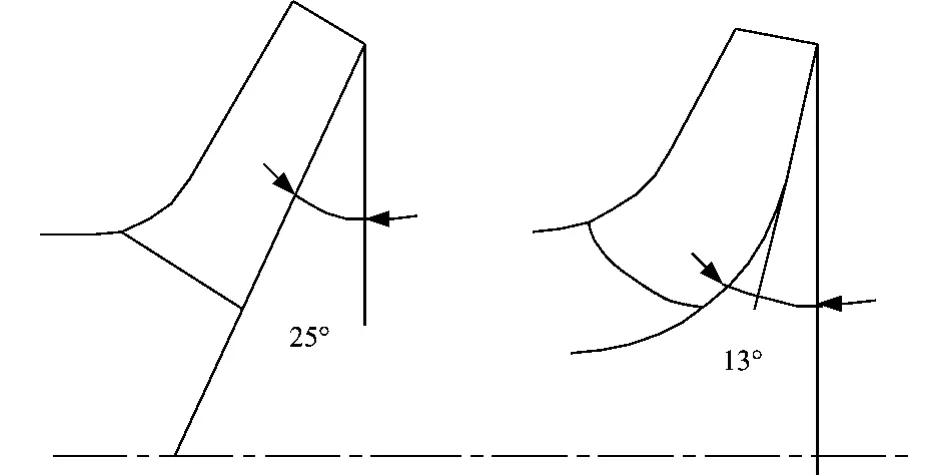
图1 两种叶轮轴面投影图

1.2 叶轮进口直径D0

井用泵因潜入水中工作，故没有吸程，不受汽蚀性能影响，因此可适当缩小叶轮进口直径，提高进口处液流速度，使密封环处泄漏量减小，容积效率提高。

以200QJ32叶轮为例，叶轮进口当量直径

式中：k0为叶轮入口系数；Q为体积流量；n为泵转速。实验中采用了两种方案。

第 一种方案：取K0＝4.015，Q＝32m3／h，n＝2 850r／min.经计算得De＝58.7mm，取轮毂直径dh＝28mm，经计算得叶轮进口直径＝65mm，经实验，设计点水泵效率η＝71.6%，高效点位于Q＝42m3／h处。

第二种方案：取K0＝3.63，Q和h同上，经计算得De＝53mm.取轮毂直径dh＝28mm，得D0＝60 mm，经实验，设计点水泵效率η＝73.2%，高效点位于Q＝37m3／h处。

对两种方案比较，选用第二种方案更为合理。

1.3 叶片进口边位置

叶片进口边位置适当向吸入口方向延伸，可以增加叶片表面积，减少单位面积负荷，使液体提早接受叶片作用。叶片进口边是按无旋流动设计的，即绝对速度的圆周分速度vu1＝0，叶片进口边向吸入口延伸时，圆周速度v01和相对速度vw1均减小，见图2，这样可以减小冲击损失，改善泵进口流动状态。延伸程度以不堵塞叶轮进口为宜。试验中200QJ20泵采取了两种方案，一组叶轮进口边延伸，一组进口边去掉4mm.实验结果为，第二组设计点扬程下降了4m，效率下降2%。试验曲线见图3。

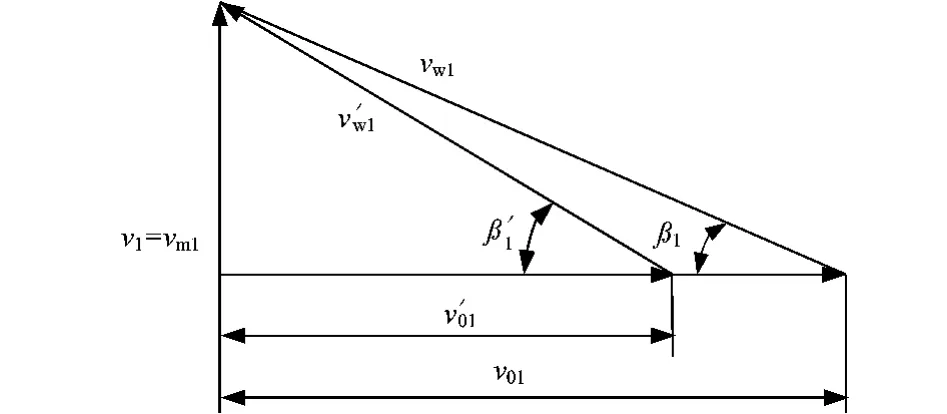
图2 叶片进口边延伸前后速度三角形

图中v1为叶片进口绝对速度；vm1为叶片进口绝对速度的轴面分速度；v01为叶片进口圆周速度（延伸前）；vw1为叶片进口相对速度（延伸前）；v′01为叶片进口圆周速度（延伸后）；v′w1为叶片进口相对速度（延伸后）。

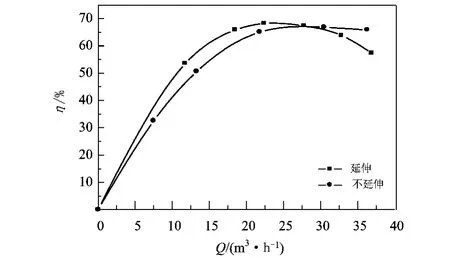
图3 叶片延伸前后Q—η曲线

1.4 叶片进口安装角

1.5 叶片进口边形状

叶片进口边均采用扭曲叶片形状。由于采用一维设计理论，假设轴面速度vm1是均匀分布的，但进口边各点v01不同，β1不同。为符合这种流动状况，需采用扭曲叶片，增加过流断面面积。

2 叶片出口参数选取与实验分析

2.1 叶片出口外径D2和叶片出口边宽度b2

对于一定性能的泵，主要是确定其出口参数（D2，b2，β2）和出口速度三角形。根据速度系数法，叶片出口直径和出口宽度为：

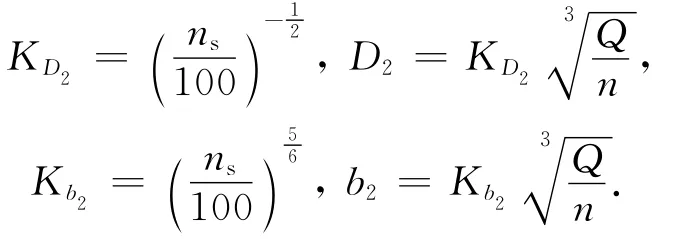
式中：ns为比转数；KD2为出口外径速度系数；Kb2为出口宽度速度系数［1－2］。

设计时依据上述经验公式，初步确定中间流线叶片出口直径和出口宽度，然后依据绘出的叶轮轴面投影图以及叶轮和导流壳匹配情况确定前后盖板流线叶片出口直径，最后根据实验结果最终确定各条流线出口直径D2。

井用泵压水室一般采用导流壳（空间导叶）结构，这样在叶轮和导流壳之间形成一个环形空间，当液流流出叶轮后突然扩散，流动方向改变，在导流壳入口处产生旋涡和冲击损失，使得泵扬程和效率下降，所以井泵效率低于蜗壳式和径向导叶式离心泵效率。为解决这一问题，往往采用加大叶片出口宽度b2的方法，提高泵扬程并使高效点适当向大流量偏移。实验结果表示，这一方法对于中低比转数可行，当设计点比转数ns＝100～200时，b2可增加5%～20%。如200QJ 20型泵，比转数ns＝103，计算出的b2＝8.13mm，最初设计时取b2＝11.5mm，比计算值增加了41%，结果高效点偏移至35m3／h处，设计点效率仅为62%，修改设计后，取b2＝9 mm，比计算值增加10.7%.实验结果为，设计点效率提高至67.7%，且高效点偏移不多，试验曲线如图4所示。

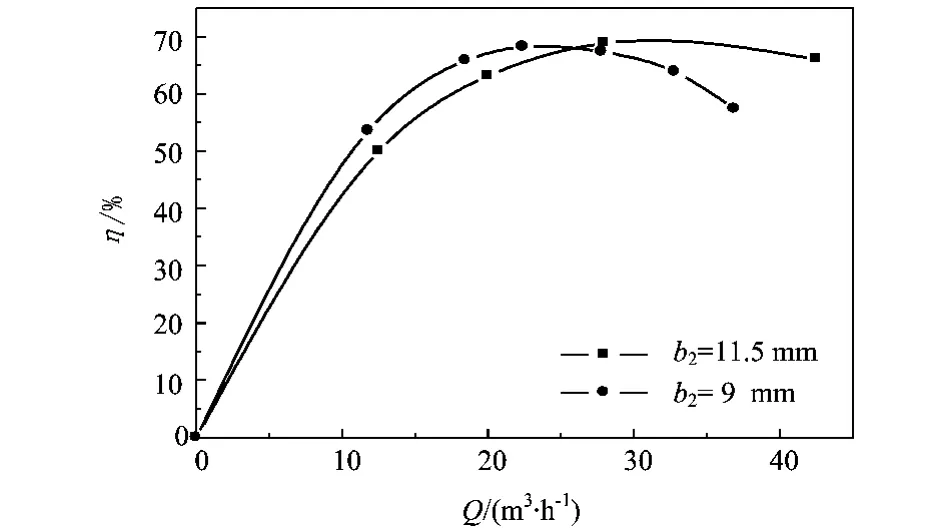
图4 不同b2时的Q—η曲线

2.2 叶片出口安装角β ［5－6］2a

由欧拉叶片式泵的基本方程，当叶轮进口无旋时（vu1＝0），无穷多叶片理论扬程为

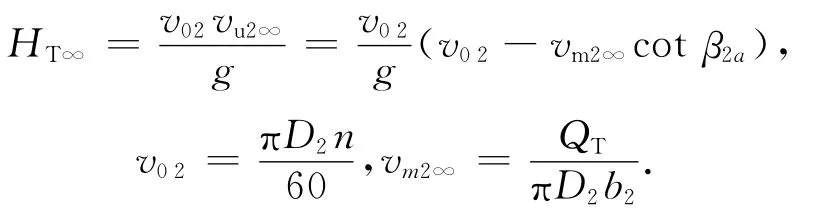
式中：QT为理论流量；v02为叶片出口圆周速度；vu2∞为无穷多叶片出口绝对速度的圆周分速度；vm2∞为无穷多叶片出口绝对速度的轴面分速度，v02∞为无穷多叶片出口绝对速度；β2a为无穷多叶片出口安装角。无穷多叶片出口速度三角形如图5所示。

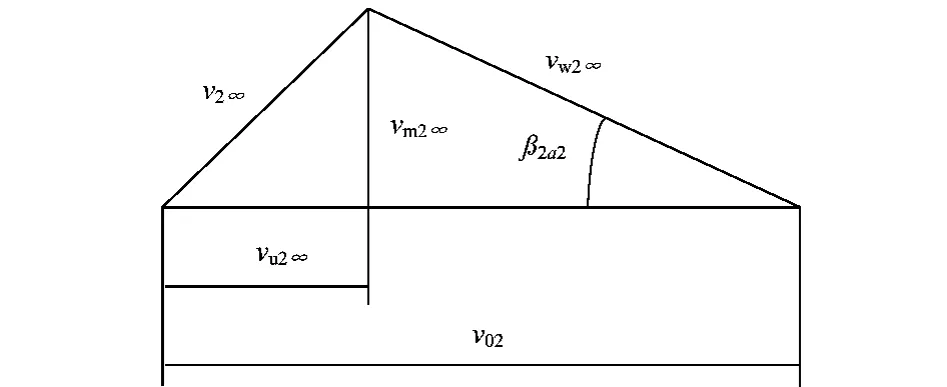
图5 无穷多叶片出口速度三角形

由速度三角形可知，当转速n和出口D2、b2一定时，vm2∞不变，当β2a增大时，可使vu2∞增大，HT∞增大，因此为了提高泵的扬程，希望β2a取得大些。但β2a越大，泵性能曲线 （Q－H 曲线）变平坦，甚至会产生驼峰，造成泵工作出现不稳定情况。另一方面，从能量角度分析，泵理论扬程可分为静扬程HST∞和动扬程Hd∞两部分，而静扬程与理论扬程之比称为反作用度τ［3］：

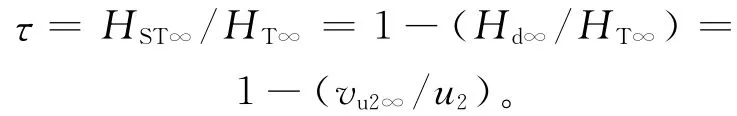
当β2a增大时，τ减小，Hd∞增加，叶轮出口处绝对速度大，使得导流壳中水力损失增加，所以希望β2a取得小些。综上所述，应根据不同的比转数，选取一个合理的β2a值。但实际上叶片都是有限的，叶片实际出口安装角β2小于β2a，井泵中一般取β2为（22°～35°），小比转数取大值。如200QJ20泵，从最初的β2＝28°，包角φ＝95°，修改为β2＝35°，φ＝90°。由于缩短了叶片长度，流道变得光滑流畅了，在其它参数不变的情况下，扬程和泵效率均有所提高。

3 导流壳参数选取与实验分析

导流壳是压水室的一种形式，又称空间导叶，是一个重要的转换能量装置。有资料表明压水室中的水力损失占泵内水力损失的40%～50%，因此设计一个好的叶轮很重要，但同时不容忽视导流壳设计。

3.1 叶轮和导流壳的合理匹配

为使叶轮和导流壳很好配合，应将二者作为一个整体来设计，即在确定叶轮轴面投影图的同时确定导流壳轴面投影图，导流壳叶片进口边尺寸与叶轮叶片出口边尺寸相匹配，导流壳叶片出口边尺寸与叶轮叶片进口边尺寸相匹配，并保证其轴面面积变化均匀，见图6。由于叶轮后盖板倾斜，前后盖板流线相差较多，因此必须斜切叶轮出口外径，否则会造成二次回流，增大水力损失。斜切角度会使泵特性曲线（Q-H曲线）产生变化，特别是对关死点扬程影响较大，斜切角度一般由试验确定，并与导流壳相互配合。

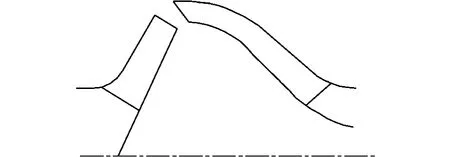
图6 叶轮与导流壳相互配合

3.2 导流壳喉部面积

导流壳叶片进口处面积称为喉部面积，是一个关键尺寸，对泵特性曲线形状和高效点位置影响很大。通过实验证明，当比转数ns＝100～250时，喉部面积S3与叶轮出口面积S2之比取1～0.7为宜，喉部断面形状为正方形时，水力半径最大，效果最好，但由于结构及空间尺寸限制，一般无法成正方形，所以要尽量接近矩形。如200QJ32型泵导流壳，最初设计时S3／S2＝1.10，结果高效点过多偏向大流量，后修改设计，使S3／S2＝0.90，结果设计点效率提高了2%，且高效点接近设计点。尽管目前人们为了提高产品通用化，希望采用一种导流壳配合多种叶轮，但从性能角度说，是不合理的。

3.3 导流壳叶片进出口安装角

3.3.1 导流壳叶片进口安装角α3

导流壳叶片进出口液流角为α′3＝vm3／vu3，再加上一个正冲角Δα3即为叶片进口安装角α3。式中vm3为导流壳叶片进口边计算点轴面速度，与流量有关，vu3为进口边计算点圆周分速度，与叶轮叶片出口速度矩有关。当ns＝100～250，一般取α3＝15°～30°，ns大的水泵取大值。

3.3.2 导流壳叶片出口安装角α4

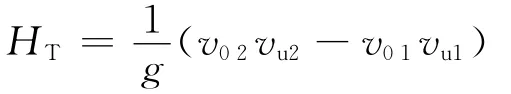
由欧拉叶片式泵基本方程可知，要想提高有限叶片的理论扬程HT，就应使vu1＝0，导流壳的一个重要作用就是消除预旋，所以取α4接近90°。式中HT为有限叶片理论扬程，vu2为有限叶片绝对速度的圆周分速度；vm2为有限叶片绝对速度的轴面分速度。

4 结论

本次设计的井用泵水力模型，是基于一维理论，根据相似理论总结出的速度系数法进行的，过流部件各参数均为比转数ns的函数，且有较大的选择范围，但各参数之间又是相互依存、相互制约的，必须综合考虑。依据上述原则设计的多种型号井用泵水力模型各项性能指标均达到和超过国家标准要求，科研成果完全转化为社会生产力，产品批量投入市场。今后应不断探索水泵设计的新理论、新方法，密切关注水泵研究新进展。

［1］ 关醒凡.泵的理论与设计［M］.北京：机械工业出版社，1987：185-240.

［2］ 辛东旭.泵设计生产新工艺新技术与质量验收标准规范实务全书（第二卷）［M］.北京：北方工业出版社，2006：423-465.

［3］ 郭丽君，何川主编.泵与风机（第三版）［M］.北京：中国电力出版社，2004：20-28.

［4］ 陈允中，曹占友，邓国强，黄红梅等.泵手册（第三版）［M］.北京：中国石化出版社，2002：268-330.

［5］ 关醒凡.现代泵技术手册［M］.北京：宇航出版社，1995：80-90.

［6］ 张景松.流体力学与流体机械［M］.徐州：中国矿业大学出版社，2009：10-46.