基于小波模极大值的铝焊缝CR图中缺陷的提取
,,
(1.南昌航空大学 无损检测技术教育部重点实验室,南昌 330063;2.洛阳中船重工,洛阳 471000;3.西安航空发动机(集团)有限公司,西安 710021)
焊缝质量在一定程度上决定了机械构件使用性能的优劣和安全性[1]。不当的焊接工艺规范会在焊接接头中产生未焊透、未熔合、焊接裂纹等金属不连续、不致密或连接不良的现象[2]。这些焊接缺陷会导致焊接构件在特定的工况条件下引发机械构件使用性能恶化,产生应力集中以及开裂等不利影响,危及工业生产及人员安全。因此,对焊接缺陷检测和质量的分析评估尤为重要。近年来计算机射线照相技术[3-5](CR)开始广泛应用到焊接质量检测,其检测结果作为焊接缺陷分析和质量评定的依据。随着现代技术的飞速发展,数字射线检测焊缝缺陷的自动提取或判别越来越受到国内外学者的关注。目前对焊接图像缺陷的边界提取一般采用高斯拉普拉斯算子或Sobel算子、Robert算子等二阶微分算法,但这些方法很容易使得微小缺陷丢失以及存在缺陷定位不准的缺点。笔者提出小波变换模极大值法[6]对焊缝区域位置、焊缝边界、缺陷所在局部区域、缺陷特征进行提取。
1 理论分析
小波变换是一种多分辨率的时频域分析方法,它突破了Fourier分析在时频域中分辨力的限制,可以聚焦到信号的任意频段,具有良好的局部化特性。由于小波变换对奇异特性敏感,使得它更适合检测图像的边缘和细节,对于某一类小波,图像边缘对应于小波变换的局部模极大值[7-9]。
设φ(x)∈L2(R),且φ(x)满足,则时,φ(x)称之为小波。定义函数f(x)的小波变换公式为:

相应的逆变公式为:

经过伸缩和平移,有φa,b(t)=a-1/2φ((t-b)/a)。其中函数伸缩系数a为频率参数,b为时间偏移量,高频小波分量对应a>1的窄带部分,低频小波偏移量对应a<1的宽带部分。这一性质使小波变换具有实现信号的时域和频域局部化的能力。若θ(x,y)在整个平面上的积分为1,并且在x或者y为无限远处收敛到0,则定义θ(x,y)为二维平滑函数。将θ(x,y)沿x或y两个方向上的一阶导数作为两个基本小波函数:

这样,图像f(x,y)的卷积型小波变换两个分量为:

对于二进小波变换,有a=2j,则:

由上式可以看出,小波变换两个分量正比于梯度矢量▽(f*θs)(x,y)的两个分量。在任一尺度2j,梯度矢量的模等于:
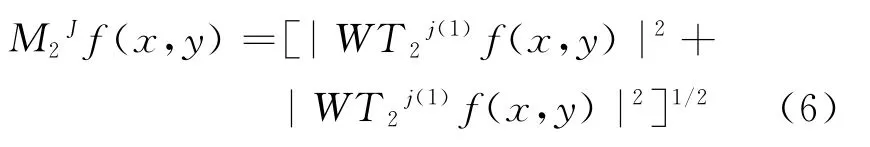
梯度矢量与水平轴的夹角为:

图像的边界即对应于沿幅角方向上模为局部极大值的那些点。将这些模极大值点的位置以及相应的模和角度大小记录下来就可以得到尺度的边界图像。
2 试验结果与分析
图1为铝焊缝原始CR透照图,图中存有未焊透、圆形、条形等缺陷,用其考察小波模极大值对边缘提取的实际效果。小波模极大值法实质上是先将小波函数和原信号卷积(连续小波变换),然后对结果取模,最后找到极大值。笔者采用二维高斯函数沿x和沿y方向的偏导函数作为小波函数基,同时设立阈值,比较每一个像素归一化的梯度值,当该梯度值大于某个阈值则是真正边缘,反之认定为伪边缘。

图1 铝焊缝原始CR透照图
图2是采用小波模极大值法并设定归一化阈值为0.2进行边缘检测,同时将结果叠加到原始图像所得到的锐化效果图。较之图1,图2更容易识别缺陷的类型、位置及其轮廓大小。
图3为图2中黑线的灰度分布图。从图中可以看出,母材的灰度值基本处于同一水平,无明显波动,而焊缝区的灰度值成山峰状剧烈变化,这是由于焊缝相比母材较厚,以及焊缝区晶粒的大小、组织的不连续所造成。通过边缘增强,可以看到在山峰顶处出现两个尖锐的毛刺,毛刺间存有凹陷,综合图2图3可以判定此为未焊透。缺陷的类型不同,其对应的凹陷或尖峰形状也不同。因此通过对曲线中的凹槽开口宽度Δw和尖峰的垂直变化量Δh来粗略判定此处是否有缺陷和缺陷类别。统计表明,对于处理后的图像,当某一列灰度曲线在焊缝区出现凹陷或者尖峰,且垂直变化度Δh<5时,可认定此处存有缺陷。在焊缝区域图像进行逐列检测后,可以准确地判定各列是否含有缺陷,以及缺陷的边界位置a1,a2。对检测到的相邻缺陷列进行合并形成小区域,其中上下边界由各含缺陷列中a1的最小值与a2的最小值确定。为防止过度分割和漏检,将相隔不超过30列的区域再次合并在一起,然后整体向外扩充20个像素,则完成缺陷局部区域确定。取区域内的各缺陷中凹陷或尖峰宽度Δw的中值,可以对区域内存在的缺陷进行粗略分类,当Δw的中值<5时可以认为区域包含裂纹类缺陷,反之则认为区域内存有非裂纹类缺陷。然后可根据裂纹类和非裂纹类缺陷的特点一一提取。图4为选择不同的归一化阈值得到的铝焊缝边缘轮廓图。对比四张图发现,当阈值偏小时,边缘捕捉得过于细化将不必要的轮廓保留,不利于缺陷识别;当增大阈值时,重要的缺陷信息被保留,不必要的细节被滤除,而当阈值过大时,细小缺陷被湮灭,因此应选择适当阈值才能较好地提取缺陷。
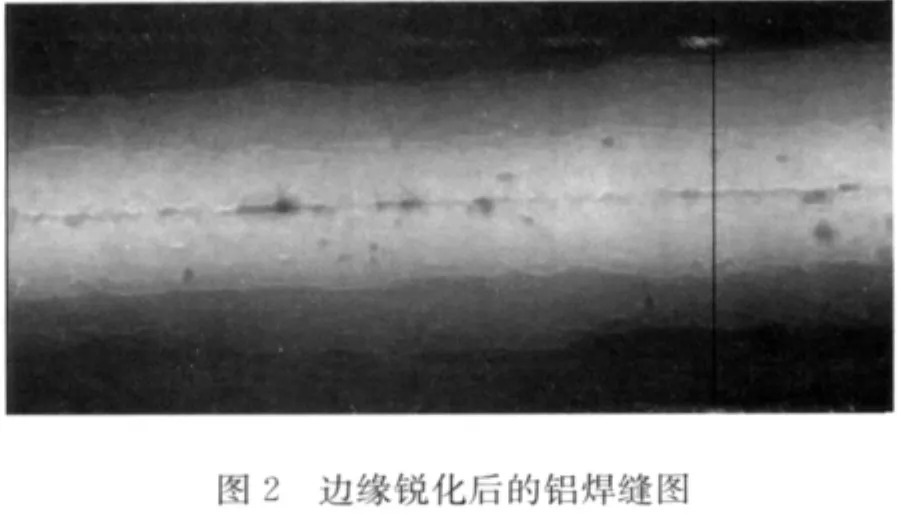

图5为分别用高斯拉普拉斯算子、Sobel算子和Robert算子对图1进行缺陷提取的结果。
通过对比可以看到,高斯拉普拉斯算子提取结果相对较差,从图中比较难确定焊缝区域。使用Robert算子和Sobel算子缺陷提取结果优于高斯拉普拉斯算子,而使用Robert算子可以模糊地看到焊趾线,Sobel算子则可以比较明显地分辨出焊接区域。但是三种方法的边缘捕捉都过于细化,不利于缺陷识别,且都不能很好地确定焊趾线,进而不能准确地确定焊缝区。由此可以看出,小波模极大值法更适用于对焊缝区域位置、焊缝边界、缺陷所在局部区域、缺陷特征的提取。
3 结论
焊缝CR图像信息丰富且复杂,使得如何精准捕捉焊缝的边界及细小的缺陷成为很有意义的研究课题。文章采用小波变换模极大值法对铝焊缝CR图进行图像处理,成功地得到焊缝区域和各类缺陷信息。试验表明,小波模极大值法能有效地将信号中含有的奇异信息提取出。对模极大值序列可进行阈值处理,可以避免奇异点出现“毛刺”或发生轻微振荡,但阈值的选择应谨慎,以免图像信息过于冗繁或丢失。


[1]张晓光,高顶.射线检测焊接缺陷的提取和自动识别[M].北京:国防工业出版社,2004,10:2.
[2]山口裕治.焊接缺陷引起的焊件断裂及其防止方法[J].国外机车车辆工艺,2008(1):12-16.
[3]张丽萍,黄廉卿.工业X射线照相技术的应用与展望[J].光机电信息,2005(1):24-28.
[4]张晓光,林家俊.X射线检测焊缝的图像处理与缺陷识别[J].华东理工大学学报,2004,30(2):199-203.
[5]杨建国.小波分析及其工程应用[M].北京:机械工业出版社,2005:107-111.
[6]张旭东,詹毅,马永琴.不同信号的小波变换去噪方法[J].石油地球物理勘探,2007,42(增刊):118-123.
[7]赵瑞珍.小波理论及其在图像、信号处理中的算法研究[D].西安:西安电子科技大学,2001.
[8]Koley C,Purkait P,Chakravorti S.Wavelet-aided SVM tool for impulse fault identification in transformers[J].IEEE Transactions on Power Delivery,2006,21(3):1283-1290.
[9]Daubechies I,Teschke G.Variational image restoration by means of wavelets:simultaneous decomposition,deblurring anddenoising[J].Applied and Computational Harmonic Analysis,2005,19(1):1-16.

