电磁超声表面波换能器发射过程的精确建模与分析
,,
(1.哈尔滨工业大学 军用电器研究所,哈尔滨 150001;2.东北轻合金有限责任公司,哈尔滨 150060)
铝合金板材是制造宇宙飞船、大型飞机、高速列车等产品的主要材料[1-2]。然而,铝板表层在运输、加工和应用过程中可能存在分层、夹杂、裂纹等缺陷,降低了产品的可靠性。传统的压电超声无损检测技术因存在盲区而难以有效检测板材的表层区域。电磁超声表面波换能器(Surface Wave Electromagnetic Acoustic Transducer,表面波EMAT)是一种非接触型超声表面波发射接收装置。该装置兼顾电磁超声换能器(Electromagnetic Acoustic Transducer,EMAT)的非接触、高效率检测优势[3]与表面波的表层缺陷敏感优势[4],为试件表层缺陷检测提供了一条有效的途径[5-6]。
为了研究和改善EMAT的性能,研究者们建立了多种EMAT数学模型[7-14]。这些模型不仅加深了研究者们对EMAT换能机理的认识,而且也为改善EMAT性能奠定了理论基础。
为了便于计算,研究者们常对现有EMAT发射过程的数学模型进行不同程度的简化[11]。例如,用二维模型代替三维实体,假设静磁场均一分布,或未考虑EMAT工作过程中发射电流产生的交变磁场的影响等[7-10]。这些简化不可避免地降低了EMAT模型的精度。为此,Jian等人在文献[12]基础上对具有螺旋线圈结构的表面波EMAT进行了建模研究,并重点考察了发射过程中交变磁场对模型精度的影响[13-14]。研究发现,忽略交变磁场的影响将会严重影响EMAT模型的精度[13]。
目前关于具有曲折线圈结构的表面波EMAT的精确建模研究仍鲜有报道。与螺旋线圈结构的表面波EMAT相比,曲折线圈结构的表面波EMAT具有更好的声场指向性,在工程中应用也更为广泛。虽然文献[13-14]中的建模方法涵盖了交变磁场的影响,能够对具有螺旋线圈结构的表面波EMAT进行精确建模,但由于曲折线圈EMAT的洛伦兹力力场很难像前者一样分解为一系列活塞力的形式[13-14],因此该方法难以有效应用于曲折线圈结构的表面波EMAT中。
笔者以铝合金板材表层检测为工程背景,针对具有曲折线圈结构的电磁超声表面波换能器的发射过程,提出了一种考虑交变磁场影响的三维精确建模方法,并在所建模型基础上对EMAT的性能进行了仿真分析。
1 EMAT换能机理及其控制方程
电磁超声换能器通常由线圈、磁铁和试件三部分组成。工程应用中,表面波EMAT常通过曲折线圈与垂直或水平静磁场相互作用,产生具有较高指向性的表面波。在非铁磁材料 (如铝、镁等)中,EMAT的工作机理以洛伦兹力机理为主,其激发电磁超声表面波的过程如图1所示。发射线圈中的高频电流(电流密度为J0)在铝板中产生交变磁场Bd和涡流密度JE。涡流密度JE将分别与交变磁场Bd以及永磁体提供的静磁场Bs相互作用,产生交变磁场洛伦兹力fd和静磁场洛伦兹力fs。两种洛伦兹力将驱使曲折线圈各匝导线下方的试件微粒做高频振动。由于曲折线圈的导线间距按照表面波波长的二分之一分布,因此试件中各质点的高频振动将发生相长干涉,从而激发出具有较强指向性的电磁超声表面波。

图1 EMAT激发电磁超声表面波的原理示意图
根据电磁学理论,EMAT在铝板中激发洛伦兹力的过程可表示为:




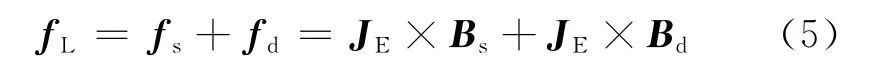

式中Hd是交变磁场的磁场强度;μm和γ分别为铝板的相对磁导率和电导率;EE是涡流产生的电场强度;fd和fs是交变磁场和静磁场分别与涡流相互作用产生的洛伦兹力密度;fL是fd和fs的合力密度;FL是在给定体积V内的洛伦兹力。
有限元方法可以有效求解公式(1)~(6)[7-11,13-14],并获得表面波 EMAT 涡流场、磁场、洛伦兹力力场的精确分布。在洛伦兹力驱动下,铝板表层将产生超声表面波。表面波的位移包括面外位移、面内径向位移和面内切向位移三个分量。图2给出了点力激发表面波的示意图。其中Fz为垂直铝板表面的点力 (简称面外点力),Fr为平行铝板表面的点力 (简称面内点力);A1,A2分别为Fz和Fr的作用点,B1,B2分别为铝板表面与A1,A2距离为r的振动质点;ξzz和ξrz分别为Fz在B1处激发的表面波面外位移和面内径向位移;ξzr,ξrr和ξfr分别为Fr在B2处激发的面外位移、面内径向位移和面内切向位移;φ为r与F h间的夹角。

图2 表面点力激发表面波的示意图
当r远大于声源尺寸时,面内点力和面外点力在铝板中激发的表面波位移由Lamb给出[15]:





若将铝板中的洛伦兹力力场区域剖分为若干单元,则各单元中的洛伦兹力可由式(6)获得。当剖分的单元体积足够小时,可将各单元中的洛伦兹力视为点力,并根据公式(7)~(11)获得各单元点力激发的表面波位移。假设力场区域被剖分为N个单元,由第i个点力FLi在声场任意一点P处激发的表面波位移为uPi,则EMAT在t时刻下P点处激发的表面波位移为:

式中(XP,YP,ZP)为P点的坐标。
2 表面波EMAT三维建模
2.1 建模流程
式(1)~(4)表明,JE与Bd的频率均与发射电流J0频率相同,因此交变磁场洛伦兹力fd的频率是静磁场洛伦兹力fs频率的两倍。式(7)~(11)表明,表面波位移的振动频率等于驱动力的频率。因此,必须首先分别计算出两种洛伦兹力产生的表面波位移,然后再将铝板上相同位置处的表面波位移分量进行矢量叠加,才能获得EMAT整体激发的电磁超声表面波。
然而,fd与fs总是随着发射电流的施加而同时存在、共同作用于铝板质点的。为了将两者彼此分离,获得各自独立的分布规律,笔者将建立两个EMAT本体模型。其中第一个本体模型描述一个完整的换能器,包括磁铁、线圈和试件三部分,称为“全模型”;第二个本体模型仅包含EMAT线圈与试件,称为“交变磁场模型”。两种模型的线圈和试件尺寸完全一致。通过有限元方法求解全模型可获得fd与fs的合力fL;通过有限元方法求解交变磁场模型可获得fd的分布;随后,根据式(5)可进一步求出fs的分布规律。
根据上述分析,笔者遵循图3所示流程建立表面波EMAT的三维模型。
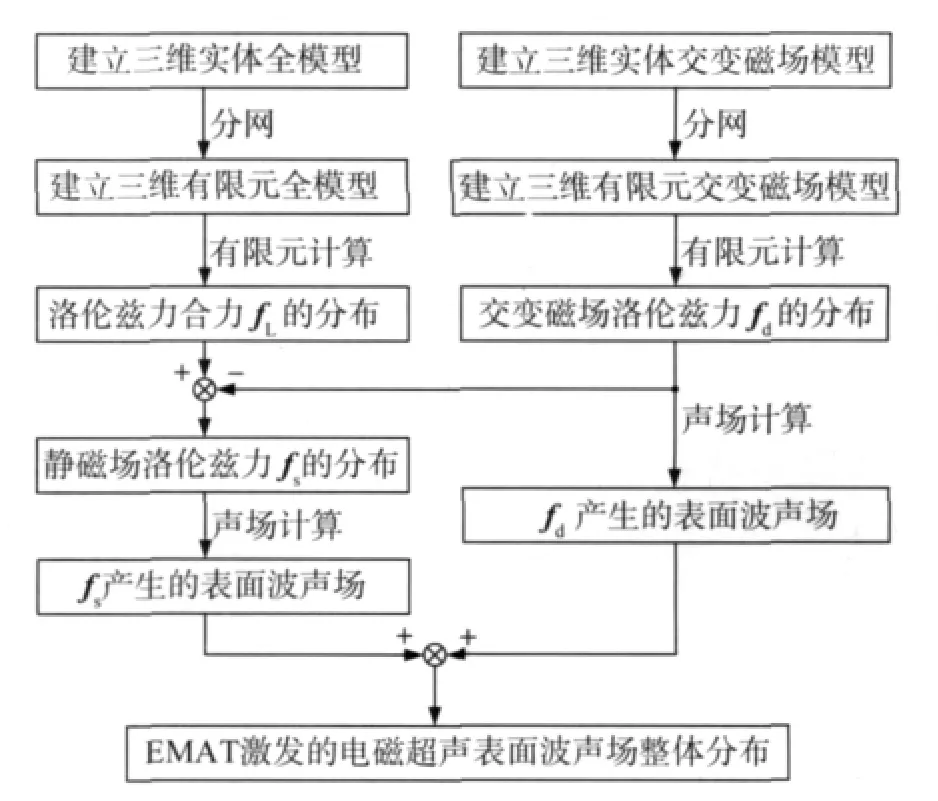
图3 表面波EMAT三维建模流程图
2.2 三维建模
采用有限元软件对铝板无损检测中常用的一个电磁超声表面波换能器进行三维有限元本体建模和计算。EMAT三维实体全模型如图4所示,包括EMAT线圈、铝板、钕铁硼永磁体、周边空气和空气远场五部分。其中EMAT线圈介于永磁体和试件之间,在图4(a)中不可见。隐去图4(a)中的永磁体、周边空气和空气远场后,EMAT线圈及铝板如图4(b)所示。图4(b)中还给出了模型所在的坐标系及发射电流的正方向,坐标系原点O位于线圈中心正下方的铝板上表面。

图4 表面波EMAT的三维实体模型
模型中曲折线圈相邻导线间距L为2.93 mm。表面波在铝板中的传播速度约为2 930 m/s,发射电流频率f为500 kHz。曲折线圈匝数为6,长35 mm,导线宽1.0 mm,厚0.05 mm,提离距离为0.1 mm。钕铁硼永磁体尺寸为60 mm×60 mm×25 mm,型号N35,剩磁1.21 T,矫顽力915 k A/m,最大磁能积279 kJ/m3。为了降低运算量,仅对包含EMAT电声能量转换的铝板区域进行建模,其尺寸为90 mm×90 mm×1.58 mm,电阻率2.62×10-8Ω·m。笔者还建立了一个不包含永磁体的EMAT三维实体交变磁场模型。该模型参数与全模型参数完全一致,隐去周边空气和空气远场后的交变磁场模型如图4(b)所示。
采用正四面体单元对实体模型进行剖分后可获得相应的有限元模型(图5)。为了提高计算精度,对EMAT换能过程中电磁场能量集中且变化剧烈的铝板表层集肤深度区域进行了网格细化。

图5 表面波EMAT三维有限元模型
洛伦兹力点力在铝板上任意位置的表面波位移可由式(7)~(11)获得。为了使fd和fs的作用区域逼近较为理想的“点力”,笔者把力场分布区域精细剖分为大量微小的正六面体单元。此外,为了方便、清晰地描述铝板中任意“质点”的表面波振动规律,铝板的整体区域(1 000 mm×160 mm×30 mm)还被剖分成大量环形网格单元(图6)。网格节点处的表面波位移可通过式(7)~(11)获得;其它位置的表面波位移可通过插值方法获得。

图6 表面波声场计算中铝板的环形网格剖分
上述EMAT三维建模方法是在电-磁-力场有限元计算与声场解析方法相结合基础上提出的。由于有限元方法可以精确地求取目前所知任何一种洛伦兹力机理的电磁超声换能器力场分布,而基于“点力”的声场解析方法可灵活地描述任何力场分布下的表面波声场信息,因此该三维建模方法同时适用于曲折线圈、螺旋线圈两种结构的电磁超声表面波换能器。
3 EMAT三维仿真分析
根据第2节提出的建模方法,获得了表面波EMAT在铝板中产生的涡流场、磁场、洛伦兹力力场以及表面波声场的分布规律。
图7给出了具有曲折线圈结构的表面波EMAT在铝板表层产生的声场分布规律。其中X轴,Y轴的方向如图4(b)所示。该图表明,该类型表面波EMAT产生的声场指向性较高,而且声场声束轴线与坐标系Y轴重合。

图7 电磁超声表面波声场在铝板表面的分布
笔者对声束轴线上各点的表面波位移进行了进一步研究。图8和9分别给出了点(0,300,0)处由fs和fd激发的表面波位移。将图8与9进行对比可知,由fs和fd激发的表面波位移具有很多相似特征,如两者的面外振幅均强于面内振幅,面外位移的相位均提前面内位移四分之一周期等。然而fs激发的表面波振幅约为fd激发表面波振幅的5倍,且后者频率为前者的2倍。


从工程应用角度来看,EMAT能够同时激发两种频率的表面波,既具有积极意义,又存在不利影响。一方面,该特性可同时采用基频和两倍频率的超声波进行检测,尤其是后者有效提高了表面波EMAT的缺陷检测能力和缺陷敏感性;另一方面,过高的敏感性会在试件表面光洁度较低时引入大量噪声,降低了缺陷回波的信噪比。因此,工程应用中,必须根据检测实际需求选择增强或抑制交变磁场洛伦兹力激发的两倍频率成分电磁超声表面波。
图10给出了具有曲折线圈结构的表面波EMAT在不同发射电流下fd和fs激发的表面波幅值。可以看出,fs和fd激发的表面波均随发射电流增加而增强,且后者增速更快;当发射电流超过528.9 A时,fd产生的表面波将强于fs产生的表面波。因此,忽略交变磁场的影响将会导致模型精度严重降低。同理,对两种洛伦兹力产生的表面波幅值随提离距离增加的变化规律进行了仿真。仿真结果表明,fs和fd产生的表面波幅值均随提离距离增加而迅速降低,且后者降速更快。因此,工程中可通过提高发射电流、降低提离距离来增强电磁超声表面波的两倍频率成分;反之,如需在不改变激发频率的前提下抑制检测灵敏度,则可通过降低发射电流、提高提离距离来减弱该两倍频率成分。

图10 不同发射电流下的表面波振幅
4 试验验证
文献[12]已证明,经过特殊设计的EMAT可有效检测出超声波的面内、面外振动速度。因此,采用该类特殊设计的电磁超声接收探头来检测表面波EMAT激发的表面波。图11给出了接收探头的工作原理示意图。当静磁场水平且垂直于线圈底边时,接收探头中的信号强度与表面波质点的面外振动速度成正比[12]。接收探头采用漆包线绕制,共20匝,厚2.5 mm,长、高均为3 mm,静磁场强度为0.63 T。

图11 EMAT检测表面波质点振动速度原理示意图
铝合金板材的尺寸为500 mm×160 mm×30 mm。试验中,表面波EMAT置于铝板一端,接收探头沿表面波声场声束轴线移动,连续测量表面波质点的面外振动速度。为了避免表面波EMAT静磁场以及铝板端面对接收探头造成干扰,仅测量了表面波声场声束轴线上受干扰较小区域的表面波信号,其测试点如图12所示。为了准确定位EMAT声场声束轴线,精确测量EMAT接收探头的位置,并确保接收探头在铝板表面沿声束轴线做直线运动,将接收探头固定在一个三维直角坐标型机器人上。接收探头可在步进电机控制下借助丝杠实现X,Y,Z三个方向上的精确运动,运动步长精度可达0.78μm。

图12 沿表面波声场声束轴线测量接收信号的示意图
将试验测量数据进行归一化处理和曲线拟合后,表面波声束轴线上电压信号随距离增加的变化规律如图13实线所示;在所建模型基础上,可计算出试验各点处的理论振动速度,其归一化、曲线拟合后的曲线如图13虚线表示。可以看出,两条曲线具有相同趋势和较好的一致性,最大偏差约为4.3%,说明所建模型具有较高精度。
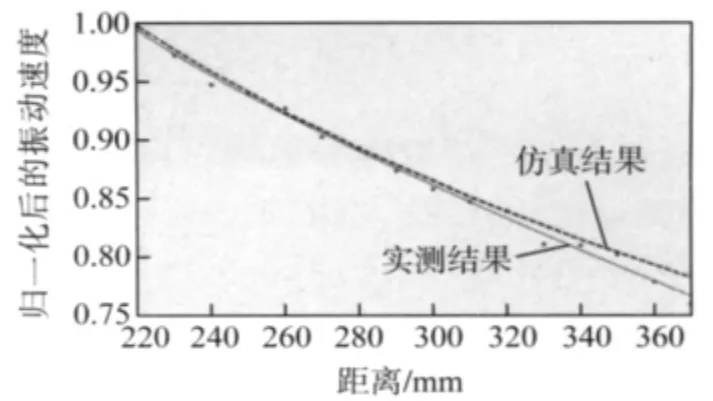
图13 归一化后振动速度实测值与仿真值的对比图
5 结论
以铝合金板材表层缺陷检测为背景,针对具有曲折线圈结构的表面波EMAT,提出了一种精确描述电磁超声发射过程的三维建模方法。该方法将有限元计算与解析方法相结合,不仅涵盖了换能过程涉及的全部物理场,而且还考虑了发射过程中交变磁场的影响。通过试验验证了模型的有效性和精确性。仿真分析表明:
(1)表面波EMAT能够同时激发出两种频率成分的表面波;其中两倍频率成分表面波增加了EMAT的缺陷敏感性。
(2)两倍频率成分表面波由交变磁场洛伦兹力产生,忽略交变磁场的影响将会降低电磁超声换能器的模型精度。
(3)两倍频率成分表面波的强度与发射电流、提离距离两个因素密切相关,增加发射电流、降低提离距离均可显著增强两倍频率成分的表面波。
三维精确建模方法不仅有助于加强电磁超声表面波换能器工作机理的认知,而且还为基于洛伦兹力机理的表面波EMAT优化设计以及电磁超声表面波无损检测技术的工程应用奠定了理论基础。
[1]王戈,王祝堂.2007年中国铝加工业述评(2)[J].铝合金加工技术,2008,36(8):1-5.
[2]张建合.高强铝合金材料的超声检测[J].无损检测,2001,23(11):479-484.
[3]Hirao M,Ogi H.EMATs for Science and Industry:Noncontacting Ultrasonic Measurements[M].Boston:Kluwer Academic Publishers,2003:199-341.
[4]Viktorov I.Rayleigh and Lamb Waves:Physical Theory and Application[M].New York:Plenum Press,1967:1.
[5]Fan Y,Dixon S,Edwards R,et al.Ultrasonic surface wave propagation and interaction with surface defects on rail track head[J].NDT&E Inter,2007,40(6):471-477.
[6]Salzburger H,Wang L,Gao R.In-motion ultrasonic testing of the tread of high-speed railway wheels using the inspection systemAUROPA III[C].Proceedings of 17th World Conference on NDT,China:Chsndt,2008:1234-1242.
[7]Shapoorabadi J,Sinclair N,Konrad A.Improved finite element method for EMAT analysis and design[J].IEEE Transactions on Magnetics,2001,37(4):2821-2823.
[8]Shapoorabadi J,Sinclair A,Konrad A.The governing electrodynamic equations of electromagnetic acoustic transducers[J].J Appl Phys,2005,97(10):10E102.
[9]Kaltenbacher M,Ettinger K,Lerch R.Finite element analysis of coupled electromagnetic acoustic systems[J].IEEE Transactions on Magnetics,1999,35(2):1610-1613.
[10]Ludwig R.Numerical implementation and model predictions of a unified conservation law description of the electromagnetic acoustic transduction process[J].IEEE Transactions on Ulrtasonics,Ferroelectrics,and Frequency Control,1992,39(4):481-488.
[11]康磊.用于铝板检测的电磁超声导波换能器优化设计技术研究[D].哈尔滨:哈尔滨工业大学,2010:1-45.
[12]Kawashima K.Electromagnetic acoustic wave source and measurement and calculation of vertical and horizontal displacements of surface waves[J].IEEE Transactions on Sonics and Ultrasonics,1985,32(4):514-522.
[13]Jian X,Dixon S,Edwards S.Ultrasonic field modeling for arbitrary non-contact transducer source[J].Proceeding of SPIE,2005,5852:515-519.
[14]Jian X,Dixon S,Grattan K,et al.A Model for pulsed Rayleigh wave and optimal EMAT design[J].Sensors and Actuators,2006,128(2):296-304.
[15]Lamb H.On the propagation of tremors over the surface of an elastic solid[J].Phil Trans R Soc,1994(203):1-42.

