双层罐底板结构立式储罐泄漏扩散数值模拟及结构优化

，

（浙江省特种设备检验研究院，杭州 310020）

立式储罐是原油、中间油、成品油、化工原料和石化产品等储存、分离、外输、中转的重要设备。储罐内存储的介质大多具有易燃易爆、易挥发甚至有毒的特性，一旦发生泄漏，极易引发火灾和爆炸，造成严重的经济损失及环境污染［1]。罐底板位于储罐的最底层，上表面接触含水的储存介质，下表面和罐基础接触，上、下表面都存在不同程度的腐蚀现象，是泄漏高发区域［2]。罐底的腐蚀状况成为评价整个储罐使用寿命的依据［3]。长期以来，罐底的缺陷一直采用定期开罐的离线方法进行检测，包括漏磁、涡流、超声、磁粉等［4]，检测需要进行停产、倒空、清洗、除锈等工序，费时费力，且停产造成的经济损失巨大。而且这些方法都是一种事后检测方法，只能进行定期检测，无法发现运行中正在发生的泄漏，而这对于储罐的安全运行至关重要。

鉴于现有检测技术的局限性和储罐罐底板腐蚀破坏的严重性，20世纪90年代中期，国外开始了双层罐底板结构立式储罐的初步研究并在近二十年内逐步成熟［5－7]，相继制定出相应的标准［8]。国内储罐建设及研究起步较晚，对于双层罐底板结构立式储罐的研究基本处于空白阶段，相关的文献也是鲜有报道。笔者所在的课题组，在吸收国外双层罐底板设计技术的基础上，提出了一种可实施泄漏在线监测的双层罐底板结构立式储罐方案。其基本工作原理为：首先，该结构能有效地避免罐底板的双面腐蚀，减少泄漏发生的可能；其次，当罐底发生泄漏时，通过通氮气吹扫的方法，将泄漏介质携带至外部监测系统，抽取并化验吹扫气体成分的变化，从而实现对储存介质的泄漏进行在线监控，一改以往的事后检测为主动监测。笔者采用计算流体力学方法，首先对两种不同罐底板结构进行了对比分析及优化研究，在此基础上，对发生在罐底夹层密闭空间内的泄漏过程进行数值模拟，分析不同泄漏位置及吹扫速度对泄漏扩散的影响规律，为开发储罐泄漏在线监测装置提供技术支撑。这对于促进双层罐底板结构立式储罐的国产化进程，以及解决储罐泄漏的安全问题具有重要意义。

1 双层罐底板结构设计

双层罐底板结构由上下两层底板及其间的支撑结构组成，除必须满足一定强度和刚度要求外，还应符合一定的流体力学要求，以确保其内流体流动均匀，从而使发生在罐底任意处的泄漏都能迅速扩散并及时被检测到。为此，笔者设计了两种完全不同的罐底板结构进行分析比较，夹层空间半径R为800mm，其结构分别为：

（1）方案1 各支撑条之间平行排列，支撑条厚度20 mm，其间距设置为400 mm，如图1（a）所示。

（2）方案2 中心设置内径为360 mm的钢质圆环，径向均布排列12根支撑条，圆环及支撑条的厚度均为20 mm，如图1（b）所示。

为使吹扫气在夹层空间进行流通，从而将泄漏介质携带至夹层空间出口，支撑结构上开有半径R′＝7 mm的半圆柱型通风孔，其中条型支撑结构上通风孔间距d＝200 mm，环型支撑结构则按角度均布，具体结构见图2。所设计的罐底板结构尺寸是现场实际储罐按一定比例的缩小，但仍大到足以反映真实情况，具体尺寸为夹层空间半径R＝800 mm，通风孔半径R′＝7 mm，循环气进出口半径r＝5 mm，泄漏孔半径r′＝2 mm，通风孔间距d＝200 mm，支撑条厚度w＝20 mm，支撑条高度h＝14 mm。

2 数值计算的模型及方法

以汽油为泄漏介质进行数值模拟，实际模拟计算区域为双层罐底板结构立式储罐罐底夹层密闭空间，以方案2的结构为例进行说明，其数值计算的物理模型如图3所示。

图3 数值计算的物理模型

由于支撑结构的存在，罐底夹层空间被分割成多个不同区域，各区域之间由通风孔相连通。数值计算模型的结构尺寸如前文所述。罐底夹层密闭空间的轴向尺寸很小，且远远小于其径向尺寸，给网格划分带来了困难。因此，对数值计算区域进行分块网格划分，在泄漏孔（图3中入口边界2）附近进行加密，网格数约为130万，并在计算过程中利用网格自适应功能对泄漏介质局部浓度变化梯度较大的区域进行加密，以提高计算结果的精度，具体如图4和5所示。

采用Fluent软件自带的无化学反应的组分输运模型研究泄漏介质的扩散问题，并将汽油挥发出来的混合介质简化为单一的物质，并在Fluent中定义其物性。在三维直角坐标系下，控制方程如下［9]：

（1）连续方程：

式中ρ为混合物密度，kg/m3；ui为i方向的速度分量，m/s。

（2）动量方程：

式中μ为流体动力粘度，Pa·s；P为绝对压力，Pa；ρa为空气密度，kg/m3。

（3）组分输运方程：

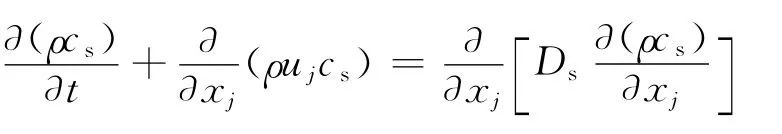
式中cs为组分s的体积浓度；Ds为组分s的扩散系数，m2/s。

边界条件如下：

（1）入口边界条件1 吹扫气入口，采用速度入口条件。

（2）入口边界条件2 泄漏入口，采用速度入口条件。

（3）出口边界 压力出口，设定为1.1个大气压的压力。

（4）外部边界 壁面边界条件，无滑移速度u＝0。

文献［10]对受限空间内气体扩散进行数值模拟，证明采用RNGk－ε对受限空间内气体扩散数值模拟可以取得较好的结果，且适用于有障碍物存在的情况。因此，数值计算中采用RNGk－ε湍流模型，且近壁面采用增强壁面函数法，以提高计算精度。计算中考虑重力对扩散的影响，采用非耦合隐式求解方法，速度与压力耦合采用SIMPLE方法，用二阶精度的迎风格式离散。

3 数值计算结果及分析

3.1 罐底板结构优化研究

从计算流体力学角度，对罐底夹层空间结构进行优化研究，旨在消除流动死区，使流动更加均匀，从而使发生在罐底任意处的泄漏都能迅速扩散，并及时被检测到。为了更好地判别夹层空间内流体均布优劣情况，引进气体分布不均匀度Mf对夹层空间内流体的分布情况进行定量分析，其表达式为［11]：

式中u i为局部速度，m/s为平均速度,

气体分布不均匀度Mf越小，表明气体速度分布越均匀，这里将此量作为考察流动空间内速度分布均匀与否的定量指标。

3.1.1 两种罐底板结构内流场的分析比较

由于罐底夹层密闭空间的高度14 mm，远远小于其半径800 mm，为减少计算量，采用不带泄漏的二维数值模拟对两种不同罐底板结构的夹层空间内流场进行比较分析。为使计算结果具有可比性，两种计算模型都采用结构化六面体网格及相同的网格步长进行网格划分，并采用相同的湍流方程、边界条件及其它求解设置进行模拟计算，模拟中不需开组分输运方程，其他设置同上，这里不再赘述。

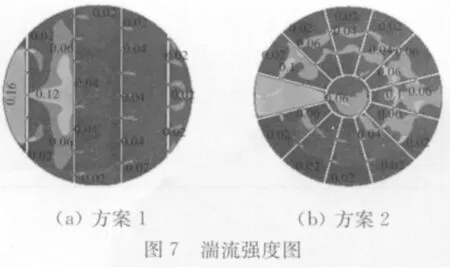
为便于比较，图6（a）和（b）显示的速度矢量放大倍数是相同的。由图6和7可以看出，两种结构具有较类似的流动规律，即在入口区域，由于流动未经衰减，具有较大的速度和湍流强度；由于前续流动损失及流动空间的扩大，当流体流至中间区域时，流体速度及湍流强度明显下降；在出口区域，由于流动空间的急剧缩小，流体流动速度及湍流强度又有所提高；且在两种结构各单独区域的拐角处都存在不同程度的流动死区。为分析比较出两种罐底板结构的优劣，分别计算了其气体分布不均匀度Mf，结果表明，方案1的气体分布不均匀度Mf1＝1.61，大于方案2的气体分布不均匀度Mf2＝1.47，说明方案2具有更好的流动均匀性。因此，选定罐底板结构方案2作为基础结构进行优化研究，以得到一种全面考虑流动均匀性及流动死区的结构形式。

3.1.2 罐底板结构内流场优化

选定的罐底板结构方案2虽然具有较好流动均匀性，但其流动区域内仍存在流动薄弱区域，倘若泄漏发生在这些地方，将很难被检测到。为消除流动死区，对选定的罐底板结构方案2做进一步改进，主要是在条型支撑结构与壁面、条型与环型支撑结构之间预留了一定的边缘距离b。对边缘距离b分别为0，5，10，15 mm的四种不同结构的罐底板结构进行数值模拟，研究边缘距离b对流动死区及流动均匀性的影响规律。

图8给出三种不同边缘距离b时，罐底板夹层空间内流体流动的湍流强度图。结合图7（b）分析可知，当边缘距离b＝0 mm时，在罐底夹层空间的个别区域，尤其是拐角处存在明显的流动死区。而当存在一定边缘距离b时，由图可见，在拐角处产生不同程度的湍动，且湍动的范围随b的增大而增大，这就有效地强化了该区域的流动，有利于泄漏的扩散。

由图9可以看出，随着边缘距离b的增大，气体分布不均匀度Mf呈递增的趋势，说明随着b的增大，气速差异逐渐增大，气体的分布越来越不均匀。究其原因，可能是由于边缘距离b存在增大了单个区域的出口面积，导致该区域的出口速度相应地降低，而该区域的出口速度又将作为入口速度进入下，都能快速地扩散，并及时被检测到，故综合考虑边缘距离对流动死区及流动均匀性影响，最终选定边缘距离b＝5 mm的罐底板结构进行后续研究。

图8 不同边缘距离下的湍流强度图

图9 气体分布不均匀度随边缘距离的变化趋势

3.2 罐底板泄漏扩散研究

在罐底板结构优化基础上，进一步对发生在罐底板夹层空间内的泄漏进行数值模拟，分析泄漏位置及吹扫速度对泄漏扩散的影响规律，以更好地指导下一步的试验研究。

3.2.1 泄漏位置的影响

固定泄漏孔半径r′＝2 mm不变，对罐底板夹层空间内流动相对薄弱的区域进行泄漏模拟，以罐底板的中心为坐标原点建立直角坐标系，则泄漏点中心位置分别为：① 钢质圆环内（0，0）；② 钢质圆环外且在圆环附近（0，250）；③ 钢质圆环外且靠近壁面（0，750）。在发生泄漏的初期，泄漏速度往往极小，取10 g/h的泄漏速度进行模拟，模拟以惰性气体氮气为吹扫介质，吹扫速度为1 m/s。查文献可知［12]，油气和氮气的质量扩散系数D＝0.03 m2/h≈8.3×10－6m2/s，油气摩尔质量65.52 g/mol。

图10给出了在一定泄漏速度下，罐底夹层空间内三个不同位置发生泄漏时出口体积分数φ随时间T的变化规律。由图可见，在该种罐底结构内，发生在位置（0，0）处的泄漏，其出口体积分数φ要明显高于其余两个位置，且φ达到稳定的时间也稍长。总体来讲，发生在三个位置的泄漏对夹层出口处体积分数φ总的影响趋势是一致的，即在泄漏初始阶段，φ几乎不随时间T的增长而增长；随着时间推移，出口体积分数φ迅速增长；当泄漏扩散趋于稳定时，φ不再随时间的变化而变化。

图10 出口体积分数随时间的变化规律

3.2.2 吹扫速度的影响

循环速度大小主要影响氮气与油气之间的传质过程，进而影响出口处扩散介质的出口浓度及扩散达到稳定状态所需的时间。以泄漏位置（0，250）、泄漏速度10 g/h为例，分别对吹扫速度v＝0，0.5，1，1.5，2 m/s进行模拟，分析吹扫速度对夹层空间出口浓度的影响规律。模拟中以30 s为时间间隔进行数据保存，当前后出口体积分数相差小于1 mg/L时，认为泄漏扩散达到稳定。

图11和12分别给出了相同泄漏位置、泄漏速度下，罐底夹层空间内泄漏扩散达到稳定时的出口体积分数φ及达到稳定所需时间T与吹扫速度v的关系曲线。由图可见，随着v的减小，φ呈增大的趋势，且速度越小趋势越明显。同样，时间T随v的增大而增大，并在v＝0时达到一个极限。v＝0时，φ取到最大值24 092 mg/L，然而泄漏扩散所需的时间也同样达到最大值135 min。

4 结论

（1）采用计算流体力学CFD方法，对两种不同罐底板结构的罐底夹层空间进行二维数值模拟。研究发现两种结构具有较类似的流动规律，且都存在不同程度的流动死区。但由于方案2的气体分布不均匀度Mf2＝1.47比方案1的Mf1＝1.61小，即方案2具有更好的流动均匀性，因此，选定罐底板结构方案2作为基础结构进行优化研究，以得到一种全面考虑流动均匀性及流动死区的结构形式。

（2）对选定的罐底板结构方案2进行结构优化研究，主要是在条型支撑结构与壁面之间预留了一定的边缘距离b。研究发现，增设边缘距离b后在原先的流动死区处产生明显的湍动，且湍动的范围随b的增大而增大。同样，气体分布不均匀度Mf随边缘距离b的增大而增大。故综合考虑边缘距离对流动死区及流动均匀性影响，最终选定边缘距离b＝5 mm的罐底板结构进行下一步模拟计算。

（3）在确定罐底板结构的基础上，模拟研究泄漏位置、吹扫速度v对夹层空间出口浓度的影响规律。结果表明，随着v的减小，φ和T都呈增大的趋势，且速度越小趋势越明显。v＝0时，出口体积分数φ及达到稳定所需的时间T都取到极限值，φ＝24 092 mg/L，T＝135 min。

［1]李一博，孙立瑛，勒世久，等.大型常压储罐底板的声发射在线检测［J].天津大学学报，2008，41（1）：11－16.

［2]刘志平，康宜华，武新军.储罐底板泄漏检测传感器设计［J].无损检测，2004，26（12）：612－615.

［3]邢菲菲.储罐罐底腐蚀声发射信号模式识别研究［D].天津：天津大学硕士论文，2008.

［4]Charlton P C，Drury J C.High speed inspection of bulk liquid storage tank floors using the magnetic flux leakage method［J].British Journal of Non－Destructive Testing，1993，35（4）：119－172.

［5]Ron Rials，Ty Hagen.Leak－detection method ensures integrity of double－bottom storage tanks［J].Oil and Gas Journal，1994，92（46）：74－80.

［6]Stephen F，Mcjones.Retrofitting hot service storage tanks with double bottoms and improved cathodic protection［J].Cathodic ＆ Anodic Protection，1992（5）：25－29.

［7]Michael B，Surkein，John Collins.Evaluation of galvanic anodes：cathodic protection design for double bottom tanks［J].Cathodis ＆ Anodic Protection，1996（5）：25－29.

［8]API 650 Welded Steel Tanks for Oil Storage［S].

［9]王福军.计算流体动力学分析—CFD软件原理与应用［M].北京：清华大学出版社，2004.

［10]王治华.受限空间内气体扩散的数值模拟及分析［D].大连：大连理工大学硕士论文，2009.

［11]杜明.双列叶片式气体分布器分布性能及结构研究［D].天津：天津大学硕士论文，2008.

［12]黄维秋，钟秦.非稳态油品蒸发的数值分析Ⅱ－数值分析及应用实例［J].石油学报（石油加工），2003，20（1）：52－57.