灰色层次分析法在导弹武器系统生存能力评估中的应用研究

邱令存 惠 轶

上海机电工程研究所，上海 200233

防空导弹武器系统是一种复杂的大系统，要对系统的生存能力[1]进行比较定位，需从多个方面进行综合评估，为此，需要提出一种全面综合的指标体系来衡量系统的生存能力。

评价生存能力的方法很多，评估的地位不同，观察角度不同，对许多系统评估问题就会有不同的理解。从上世纪九十年代，国内外相继出现了多种评估方法，包括层次分析法、指数法、专家评价法、SEA方法、模糊综合法、WSEIAC模型、作战模拟法等，每种方法各有其适用性与局限性。近年，以信息不完备系统为研究对象的灰色理论得到了快速发展，而武器系统的复杂性，以及在作战使用过程中情况的多样性、不确定性使导弹武器系统具备了不完备系统的特征。由此，灰色系统理论[2-4]在对武器系统的研究中得到了广泛应用。本文就是在以往灰色系统理论的基础上，对系统的白化权函数进行了改进，并结合层次分析法提出了一种新型导弹武器系统生存能力评估模型。

1 武器系统生存能力的指标体系

生存能力是指挥自动化系统的一个重要指标，代表了导弹武器系统的一项基本能力。具体可以从防御能力、战斗能力、反应能力和恢复能力四个方面来衡量[5]。防御是系统生存能力中最基本和最主要的方面，反映了系统抗击打、抗毁的能力。战斗能力则从另一角度诠释了生存能力，进攻是最好的防守，能准确、有效的打击、消灭敌人才能最大限度的保存自己。反应能力反映了系统的机动性和灵活性。恢复能力决定了武器系统在遭受打击、部分已经损毁的情况下能够进行自我恢复的能力。根据以上分析，为导弹武器系统的生存能力建立一套综合指标体系，如图1所示。

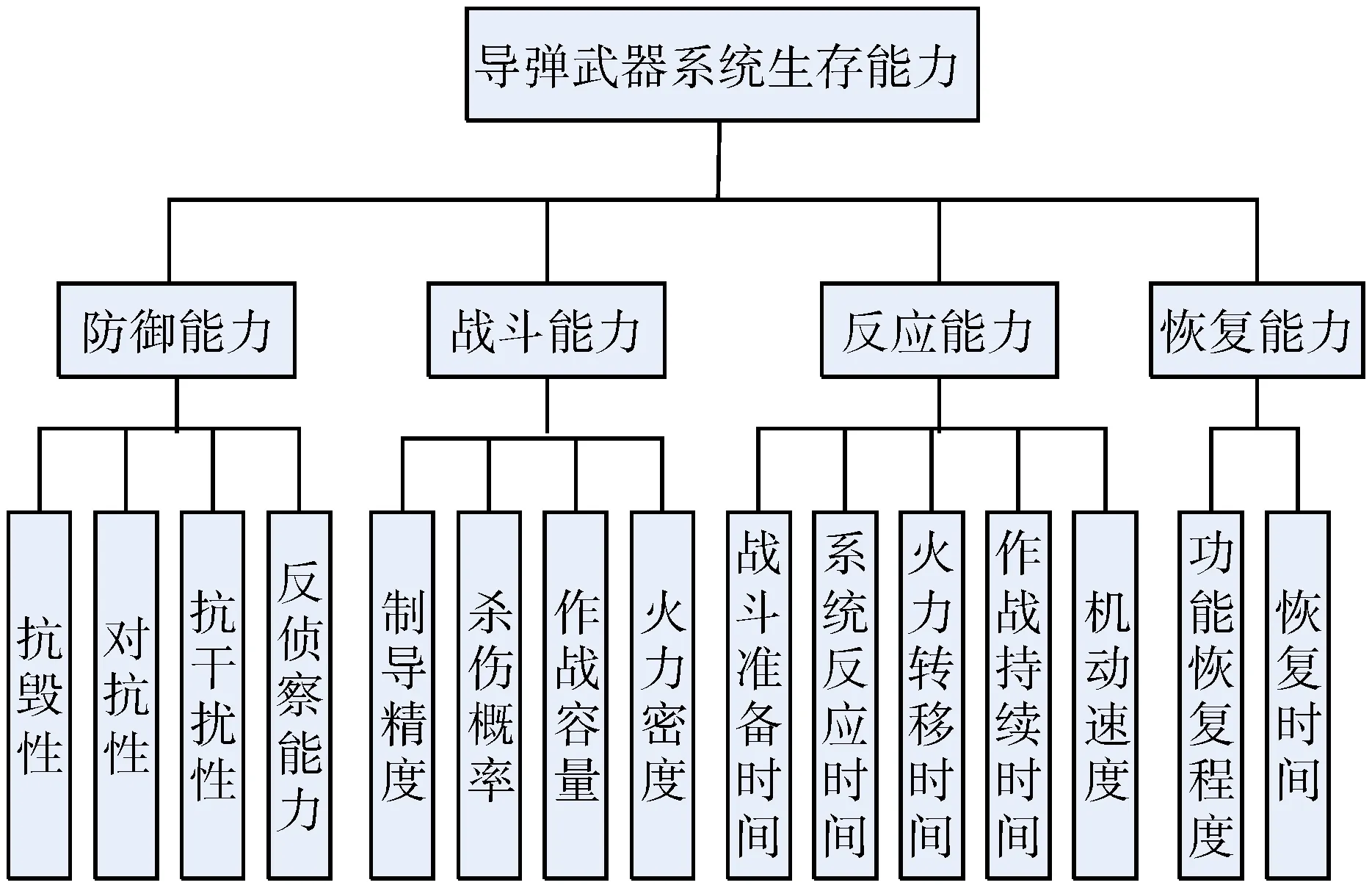
图1 导弹武器系统生存能力指标体系图

2 灰色系统理论

灰色系统理论是以灰色系统为研究对象，运用控制论与运筹学相结合的数学方法发展的一套理论和方法。

研究灰色系统，首先要确定评价灰类，即要确定评价灰类的等级数、灰数以及白化权函数。其中灰数表示统计指标对应的等级，灰数中的数值分别表示评分可能分布的区间，中间的数值表示属于该灰类的最佳评分值。

白化权函数的选取和确定对系统研究结果的准确性和科学性是有很大影响的。本文根据导弹武器系统评价指标的特性，结合以往白化权函数的选取方法[2]，在中心点三角白化权函数[6]的基础上对端点取值进行修正，得到新型中心点三角白化权函数。其表达如下：

设定灰类数为S，选取λ1，λ2，…，λS为最属于灰类1，2，…，S的点(以属于灰类最大可能性为选取依据，称为中心点)，其中，λ1>λ2>…>λS，取白化权函数为：

(k=2，3，…，λS-1)

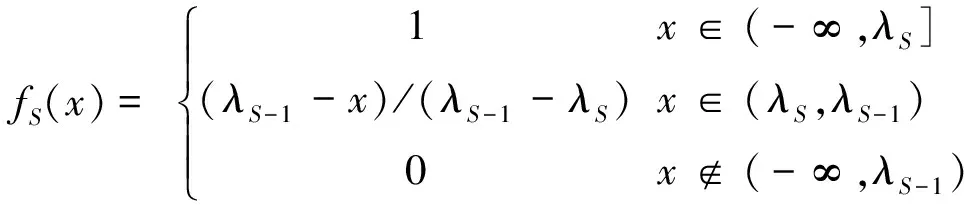
不难证明，修正后中心点白化权函数满足：

定理1：不存在两个以上白化权聚类交叉现象。

定理2：白化权聚类某指标取值属于各灰类系数之和为1。

3 武器系统生存能力评估

3.1 建立判断矩阵并确定指标权重

设武器系统有n个技术指标，通过指标间两两重要性对比进行打分，建立判断矩阵A。判断标度采用层次分析法常用的1～9标度[7]。

为克服一位专家确定指标权重时带有的主观性问题，需要确定n个技术指标的权重。

对判断矩阵A，采用“和积法”求出其最大特征值λmax和对应的特征向量W，即：

AW=λmaxW

其中，W的分量(W1，W2，…，Wn)是对应于n个技术指标的相对重要程度，即权重系数；λmax为最大特征值。

为进一步避免专家的主观错误，需对判断矩阵A进行平均随机一致性(CR)检验，当CR≤0.1时，则认为判断矩阵的一致性可以接受，否则重新构造矩阵。

CR=CI/RI，

其中，CI=(λmax-n)/(n-1),RI按表1取值。

表1 RI取值表

3.2 确定评价样本矩阵

对于p个评价指标，有q个专家参加评价，第k个评价者对指标i给出的评价为bik，则可得评价样本矩阵B。

3.3 确定评价灰类

确定评价灰类即需要确定评价灰类的等级数、灰数以及白化权函数。

在指标的评价中，将指标的评分等级划分为优秀、良好、中等、较差、很差5个等级，赋予他们相应的分值为90,80,70,60,50。即系统的等级数为5，灰数为90,80,70,60,50。根据第3章中的描述，选取白化权函数如下：

1)灰数⊗1∈(80,90,+∞)，其白化权函数为

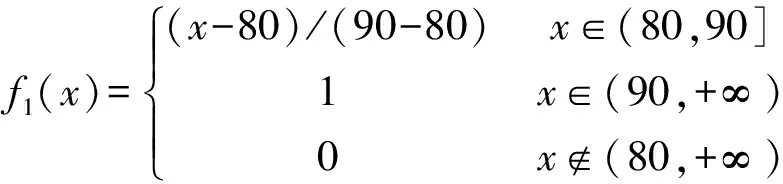
2)灰数⊗2∈(70,80,90)，其白化权函数为

3)灰数⊗3∈(60,70,80)，其白化权函数为

4)灰数⊗4∈(50,60,70)，其白化权函数为

5)灰数⊗5∈(-∞,50,60)，其白化权函数为

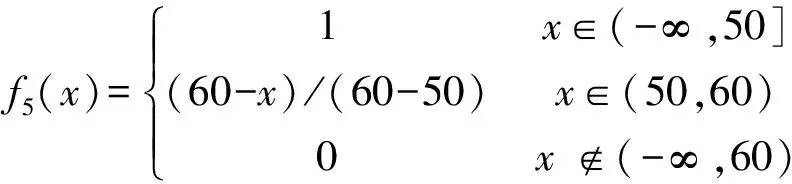
3.4 计算灰色评价权向量及矩阵

对于评价指标i，第e个评价灰类的灰色评价系数记为xie，各个评价灰类的总灰色评价系数记为xi，属于第e个评价灰类的灰色评价权记为rie，则：

,,rie=xie/xi。

从而有灰色评价向量ri：

ri=(ri1,ri2,ri3,ri4,ri5)。

将p个评价指标对应于各评价灰类的灰色评价权向量综合后，得到灰色评价矩阵R：

3.5 计算结果

假设p个评价指标的权重向量为W，其综合评价结果记为C，则：

C=W·R=(c1,c2,c3,c4,c5)

对C所提供的信息可按最大隶属度原则确定被评估对象所属的灰类等级。

4 某武器系统生存能力计算

图1中给出了武器系统生存能力的指标体系，由上到下分为3层。

专家对导弹武器系统的指标通过两两重要性对比进行打分，得到的判断矩阵为：

用“和积法”求得各矩阵的特征向量、特征值和检验值分别为：

W总评=(0.2185,0.5339,0.1754,0.0721),

λ总评=4.141,CR=0.0525；

W防御=(0.1259,0.1705,0.5152,0.1884),

λ防御=4.0936,CR=0.035；

W战斗=(0.2539,0.4683,0.0990,0.1788)，

λ战斗=4.0215,CR=0.0081；

W反应=(0.2223,0.3410,0.2499,0.1190,0.0678),

λ反应=4.0936，CR=0.0204；

W恢复=(0.3333,0.6667),λ恢复=2，CR=0。

由上述结果可知，各判断矩阵具有良好的一致性。

5个专家对各分指标的打分如表2所示。

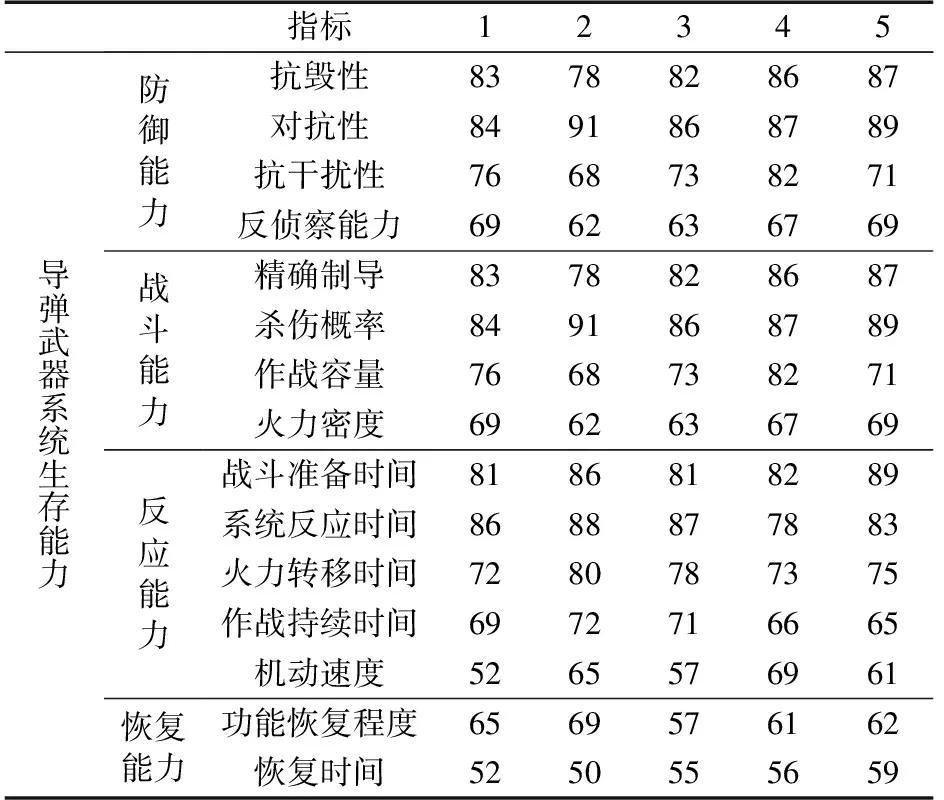
表2 专家打分表

以3.4中介绍的灰色评估法计算所得到的防御能力、战斗能力、反应能力、恢复能力的灰色评价矩阵为：

其中，矩阵中各行表示相应子因素属于优秀、良好、中等、较差、很差的程度。

相应的防御能力、战斗能力、反应能力、恢复能力的评价结果向量为：

C防御=(0.1887, 0.3088, 0.4066, 0.0960, 0)

C战斗=( 0.4193, 0.3656, 0.1750, 0.0400, 0)

C反应=(0.2482, 0.4486, 0.2320, 0.0563, 0.0149)

C恢复=(0, 0,0.1133, 0.4933, 0.3933)

上述结果表明，该系统的防御能力“中等”，战斗能力“优秀”，反应能力“良好”，恢复能力“较差”。

进行多层次灰色综合评价，得到的最后评价结果为：

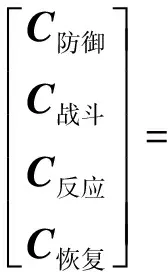
(0.2927, 0.3335, 0.2017, 0.1423, 0.0298)

依据最大隶属度原则，该导弹武器系统综合能力处于“良好”水平。判断结果符合该武器系统的技术特征和专家预判，同时验证了该生存能力评估模型的适用性。

5 结论

白化权函数的构建是灰色评估系统的关键一步，本文构建的白化权函数具备“两个以上白化聚类不交叉”和“各灰类系数之和为1”两个特点，确保了系统评价的科学性和客观性。另外，本文所述的灰色评价法将评价者的分散信息处理成一个描述灰类程度的权向量，并且能够分析各评价指标的灰类分布情况。最后，对其进行单值化处理，把武器系统效能的定性分析转化为定量分析。本文给出的某武器系统生存能力评估案例证明该方法是切实有效的，本方法不但可以用于单个系统不同性能间的评价，也可以对多个系统的综合性能进行比较。

参 考 文 献

[1] 徐品高.防空导弹体系总体设计[M].第一版.北京:宇航出版社,1996,5.

[2] 刘海燕，史志富.导弹武器系统作战效能的灰色评估[J].航空兵器，2005,(6):11-14.(LIU Hai-yan，SHI Zhi-fu.Performance Evaluation of Missile Weapon System with Grey Evaluation[J].Aero Weaponry, 2005,(6):11-14.)

[3] 李源,王鹏华,安海明.基于三角白化权函数的信息化炮兵旅作战效能灰色评估[J].舰船电子对抗,2008, 31(6):40-42.(LI Yuan,WANG Peng-hua,AN Hai-ming.Grey Evaluation of Operation Efficiency for Informationized Artillery Brigade Based on Triangle Whitening Weight Function[J].Shipboard Electronic Countermeasure, 2008, 31(6): 40-42.)

[4] 潘光辉,娄寿春.防空导弹C3I作战效能灰色评估[J].弹箭与制导学报,2005, 31(6):811-813.(PAN Guang-hui,LOU Shou-chun.The Grey Evaluation of Air Defence Missile of C3I Fighting Efficiency[J].Journal of Projectiles,Rockets,Missiles and Guidance, 2005, 31(6):811-813.)

[5] 陈怀谨.防空导弹武器系统总体设计和试验[M].北京：宇航出版社，1995.

[6] 刘思峰, 谢乃明.基于改进三角白化权函数的灰评估方法[C].第16届全国灰色系统学术会议论文集,2008.

[7] 王莲芬，许树柏.层次分析法引论[M].北京：中国人民大学出版社，1990.