含无序量测的多传感器目标跟踪滤波算法

蒋春蕾

西昌学院汽车与电子工程学院，四川西昌 615013

在飞行器的分布式多传感器融合跟踪系统中，由于通信链路随机时间延迟，以及各传感器的量测预处理时间不同，多传感器量测数据通过多条数据链路传输到中心处理器时，常会发生多传感器量测数据不按正常时序到达融合中心的情况，即出现所谓的无序量测现象(Out Of Sequence Measurement, OOSM)。目前针对此问题主要的处理方法分为4类[1]：重新滤波法、数据缓存法、丢弃滞后量法和直接更新法。其中，重新滤波法、数据缓存法的计算量较大，影响了飞行器跟踪系统的实时性；丢弃滞后量法容易造成大量有用信息的丢失，导致跟踪系统的精度严重下降；直接更新法的存储量和计算量都很小，滤波输出没有滞后，而且具有潜在的高精度滤波性能，是实时多传感器组合跟踪系统的最佳选择。本文在直接更新法的基础上，提出一种新的飞行器跟踪滤波方法，解决分布式多传感器目标跟踪滤波中的无序量测问题，实现对飞行目标的高精度跟踪。

1 描述飞行器空间状态的常用坐标系

用于测量飞行器状态需要用到的坐标系主要有：地心惯性坐标系、星体坐标系等。坐标系的3个基本要素是坐标原点、基本平面(x轴和y轴所在平面)及正法向(右手系)，基本平面上的主方向(z轴方向)。

1.1 地心惯性坐标系

该坐标系的坐标原点为地球质心Oe，其x轴指向标准历元2000.0(即2000年1月1日12时)的平春分点，基本平面为该标准历元时刻的平赤道面，z轴与x轴垂直，并指向该标准历元时刻的平天极，z轴在基本平面内与x轴、y轴构成右手系。

1.2 星体坐标系

在该坐标系中，坐标原点Os为观测卫星的质心，基本平面为观测卫星的轨道面，z轴从坐标原点Os指向地球质心Oe，x轴在基本平面内与z轴垂直并指向卫星运动方向，z轴垂直于基本平面并与x轴、y轴构成右手系。

1.3 坐标系的相互转换

地心坐标系与星体坐标系的坐标转换可分2步进行。首先进行坐标平移，将地心惯性系中的坐标平移到以观测卫星质心Os为原点的空间坐标系；其次进行坐标旋转，将以观测卫星质心Os为原点的空间坐标系的坐标转换到相应的星体坐标系。具体转换方法详见文献[2]。

2 飞行器运动状态模型和测量模型

2.1 飞行器运动状态模型

(1)

则飞行器运动的状态微分方程为：

(2)

其中F(·)表示状态变量X的非线性变换。

μ

(3)

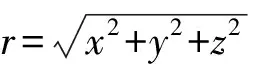
2.2 飞行器姿态测量模型

观测模型描述了目标的三维空间位置到目标像平面位置的映射过程。设地心坐标系下的目标位置为r=[xyz]T，卫星位置为rs=[xsyszs]T，(·)T表示矩阵转置，则将目标位置r映射到像平面位置需要经过一系列坐标系转换，依次为地心坐标系⟹轨道坐标系⟹星体坐标系⟹传感器坐标系⟹像平面坐标系。

根据成像模型的逆过程计算出目标飞行器所在的方位角βk和俯仰角εk，其定义分别如下：

(4)

(5)

将测量矢量定义为Z(k)=[βkεk]T，则测量矢量可以表示为状态变量X的非线性函数：

Z(k)=H(X(k))+n(k)

(6)

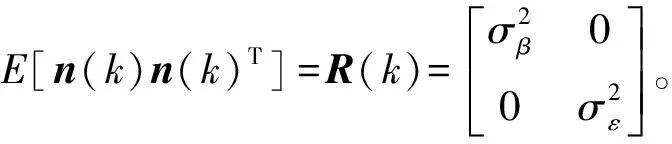
3 跟踪滤波算法与仿真

3.1 扩展卡尔曼滤波算法

由于目标飞行器中段的状态方程是非线性连续方程，测量方程是非线性离散方程，这里采用扩展卡尔曼滤波(Extend Kalman Filter, EKF)方法[3]来估计目标飞行器的状态，首先需要对状态方程和测量方程进行离散化和线性化，其处理过程如下：

对目标飞行器的状态微分方程(2)式进行离散化，可得：

(7)

当时间间隔tk+1-tk=T足够短时，F(X(t))可以在tk附近展开为Taylor级数：

F(X(t))≈f(X(k))+A(X(k))·

F(X(k))·(t-tk)

(8)

X(k+1)=X(k)+F(X(k))·T+

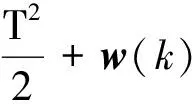
(9)

由(2)式及矢量微分法则[4]，A(X(k))可以表示如下：

(10)

//(k/k))·T+

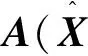
(11)

根据状态转移矩阵Φ(t,tk)的定义[5]，可以将其在tk附近展开为Taylor级数：

(t-tk) +O(t-tk)

(12)

根据状态转移矩阵的性质可得：

Φ(tk,tk)=I

(13)

(14)

将上两式分别代入(12)式，可表示为：

Φ(t,tk)=I+A(X(k))·(t-tk)+O(Δt)

(15)

同样地，对连续状态转移矩阵进行离散化后可得：

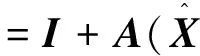
(16)

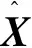
(17)

由式(4)和(5)及文献[2]中的坐标转换公式ρ=GT(rT-ρO)，可得：

(18)

(19)

(20)

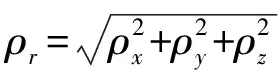
将状态方程和测量方程线性化、离散化后，即可将其代入如下所示的扩展卡尔曼滤波公式进行迭代计算。为便于表示，这里将递推的时刻转换为矩阵的下标来表示。

(21)

在这里Q矩阵表示由于非线性状态方程线性化时引入的误差，一般可通过经验选取为较小的常数矩阵[6]。

计算滤波增益矩阵：

(22)

计算状态滤波更新及相应的协方差矩阵：

(23)

Pk+1=(I-Kk+1Hk+1/k)Pk+1/k

(24)

3.2 多步滞后无序量测处理算法

观测卫星系统在下传角轨迹数据时，可能由于传输距离或者预处理时间的不一致，导致较早的测量数据反而较晚到达数据融合中心的现象，即所谓的无序量测现象，该情况如图1所示。

图1 无序测量示意图

目标飞行器的中段运动模型可视为二体运动模型，其状态方程和测量方程可表达式为：

X(k+1)=f(X(k),k)+w(k)

(25)

Z(k)=h(X(k),k)+n(k)

(26)

其中噪声协方差为：

E[w(k,j)w(k,j)T]=Q(k,j)

E[n(k)n(k)T]=R(k)

(27)

在无序量测Z(d)到达之前，系统状态已经更新到t(k)状态。根据3.1节中扩展卡尔曼滤波算法得到最新的预测估计状态和协方差：

E[X(k),Zk]

(28)

P(k|k)cov[X(k),Zk]

(29)

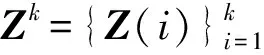
Z(d)=h(X(d),d)+n(d)

(30)

计算从t(d)时刻到t(k)时刻的预测方程和预测协方差：

E[X(k),Zd]

(31)

P(k|d)cov[X(k)|Zd]

(32)

P(d|k-l)=(Φ(k-l))P(k-l|k-l)

(Φ(k-l))T+Q(d,k-l)

(33)

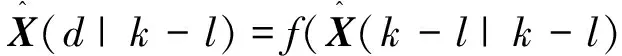
(34)

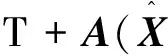
(35)

下面给出多步无序量测的计算步骤：

P-1(d|d)=P-1(d|k-l)+

(H(d))TR-1(d)(H(d))

(36)

(37)

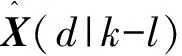
(H(d))TR-1(d)Z(d)

(38)

Step 2：计算从t(d)到t(k)预测状态方程及协方差：

P(k|d)=(Φ(d))P(d|d)(Φ(d))T+Q(k,d)

(39)

(40)

假设P(k|d)和P(k|k)不相关可得等式：

P-1(k|k,d)=P-1(k|k)+P-1(k|d)

(41)

但是P(k|d)和P(k|k)根据相同的预测模型分享共同的历史数据(如P(k-l|k-l))，所以两者是具有相关性的，为了得到独立的信息，就得去除无关的信息。

P-1(k|d)D=P-1(k|d)-P-1(k|k-l)

(42)

(43)

Step 4：计算状态滤波更新及相应的协方差矩阵：

P-1(k|k,d)=P-1(k|k)+P-1(k|d)D

(44)

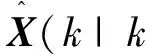
(45)

3.3 算法的仿真分析

仿真场景设置：采用2颗卫星同时对目标飞行器进行观测，采样时间间隔为4s，取飞行器在空间飞行的500～600s弧段作为观测时间段，视线误差为100μrad。仿真分单步延迟量测、两步延迟量测和多步延迟量测3种情况进行讨论。

(1)单步延迟量测

卫星1的量测数据按正常时序到达中心处理器，卫星2的量测数据固定作单步延迟，图2为卫星测量时间与到达时间的时序关系描述。

图2 卫星的测量时间和到达时间描述图

为了简化描述，将扩展卡尔曼滤波算法简称为EKF，基于扩展卡尔曼的前向预测多步滞后无序量测处理算法称为EKF-OOSM，CRLB为克拉美罗下限。将本文的EKF-OOSM算法与传统的丢弃算法、EKF算法进行对比，各算法的仿真结果如图3所示。

图3 单步延迟情况的位置速度均方根误差

(2)两步延迟测量

将卫星2的测量数据作两步固定延迟，其它参数设置与单步延迟相同，各算法的仿真结果如图4所示。

(3)多步延迟测量

将卫星2的测量数据作多步固定延迟，其它参数设置与单步延迟相同，各算法的仿真结果如图5所示。

图4 两步延迟情况的位置速度均方根误差

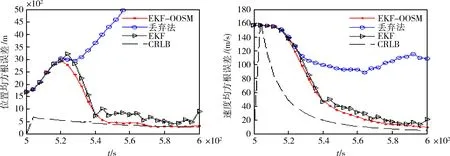
图5 多步延迟情况的位置速度均方根误差

从图3、图4和图5的仿真结果可以看出，丢弃滞后量数据的滤波算法(即丢弃算法)的滤波效果很差，测量目标飞行器时得到的位置误差和速度误差与克拉美罗下限CRLB相差太大，特别是位置误差还有可能导致滤波结果不收敛。扩展卡尔曼滤波算法EKF在整个观测时间内，测得的位置误差和速度误差有抖动，滤波效果不平滑，有起伏现象，测量精度不高，其测量的位置误差、速度误差较大。与丢弃算法、扩展卡尔曼滤波算法EKF相比，采用EKF-OOSM滤波算法得到的目标飞行器的位置误差、速度误差较小，接近理想状态的克拉美罗下限，而且在整个观测时间内，滤波结果较为平滑，测量误差收敛性较好，能够满足对目标飞行器数据的精确处理要求。

4 结束语

本文提出了一种针对无序量测数据的多传感器目标跟踪处理算法。首先针对多传感器系统对目标飞行器的跟踪测量问题，介绍了地心惯性坐标系和星体坐标系的定义及转换公式，在此基础上给出目标飞行器的运动状态方程和测量方程，然后结合扩展卡尔曼滤波算法，推导了基于扩展卡尔曼滤波的前向预测多步滞后无序量测处理算法，最后分别对不同时间步长滞后的情况下目标飞行器跟踪测量问题进行了仿真分析，仿真结果表明采用该算法处理目标飞行器的位置和飞行速度，得到的误差较小，在整个观测时间内，测量误差的收敛性较好，可以实现对目标飞行器的精确测量和跟踪。

参 考 文 献

[1] 韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M].北京: 清华大学出版社,2006:25-35.

[2] 肖业伦.航天器飞行动力学原理[M].北京:宇航出版社,2005:203-205.

[3] 李强.单星对卫星目标的被动定轨与跟踪关键技术研究[D].长沙:国防科技大学,2007.

[4] 叶其孝,沈永欢.实用数学手册(第2版)[M].北京:科学出版社,2006.

[5] Steven M. K. Fundamentals of Statistical Signal Processing Volume I: Estimation Theory [M].Pearson Education, Inc, 1993.

[6] 盛卫东，林两魁，安玮，周一宇.基于全局最优的被动多传感器多目标轨迹关联算法[J]. 电子与信息学报,2010,37(7):1621-1625.(Sheng Wei-dong,Lin Liang-kui,An Wei,Zhou Yi-yu.A Passive Multisensor Multitarget Track Association Algorithm Based on Global Optimization[J].Journal of Electronics and Information Technology,2010,37(7):1621-1625.)