地铁站人群规律及特征研究—以广州地铁为例

罗凤霞，王光辉，杜帅楠， 王英杰，胡 成

（1. 广州市地下铁道总公司，广州 510030；2.中国科学院 科技政策与管理科学研究所， 北京 100190；3. 河南大学 应急管理研究所， 开封 470004；4. 中国铁道科学研究院 电子计算技术研究所，北京 100081；5.北京市劳保保护科学研究所， 北京 100054）

随着人口规模的不断增加、城市范围的不断扩展以及交通压力的不断突现，各大城市针对本地的基本情况，分别发展和完善相应的城市轨道交通（地铁）系统。由于地铁具有运行速度快、车次多、旅客运送量大以及运行稳定等特点，人们将其作为工作或出行的主要交通工具之一。尤其在早高峰和晚高峰时段，地铁站可能成为人群流量或人群密度集中的地方。本文以广州地铁为例，深入分析地铁车站闸机及视频监控资料，挖掘地铁车站大客流人群流动规律，为突发事件下的应急疏散模拟研究提供基础数据。

1 密集人群流动规律内涵及其分析指标界定

1.1 密集人群流动规律的内涵

人群流动规律是指人群行走时表现出来的群体运动规律，通常被称为人行走规律、人群运动规律、行人运动规律等。人群流动规律包括宏观规律和微观规律。宏观规律主要指行人集体所表现出来的密度、速度和流量等特征；微观规律主要指单一行人在某段时间内因其心理和生理因素的影响而表现出来的决策行为和采取的动作[1]。尽管人的行为比较复杂，会在一定程度上表现出无序性，但其行走仍然可以找到一定的规律性，尤其是人群拥挤时，人的运行互相受到其他人的影响，人群的运动表现出一些单一个体不具备的群体特征。常见的人群流动规律或现象包括：

（1）人群密度越大，由于身体间的相互影响，人群速度越慢。

（2）人们对于绕道或者反向运动表示出强烈的厌恶心理；行人总是与他人或公共设施边界保持一定的距离；行人有时会重复别人的行为方式；在拥挤场合，人群通常会因为恐慌造成推挤和惊跑，从而导致冲撞践踏并引起伤亡事故等。%

（3）密集人群中双向流动会产生“自动队列”的自组织现象。自组织不是提前刻意计划、组织形成的，比如通过指示牌、法规和习惯等方式，而是一种自然现象。“自动队列”现象是指在双向人流中，行走方向大致相同的行人之间形成条状的通道，后面的行人跟随前面的行人前进。

（4）当人群通过一个入口或出口处时，若有次序地行进，可顺畅流通。行进速度愈快则流量愈大。而当人群很拥挤时，则流量大大减少。这就是所谓的“瓶颈效应”。

（5）整个人群同步接受到紧急撤离信息后，同步或在相近时间内做出响应行动，当出口的宽度限制了密集人群的流动时，导致密集型人群移动在出口处形成聚集，呈现拱形分布的特点，如图1[2]。

1.2 人群流动规律的分析指标界定

自上世纪初期以来，密集人群流动规律的研究逐渐成为行业的热点，并为人群疏散提供理论支持。学者通过采取观测和统计分析的方法对人群流动的基本特征进行分析，具体包括人群组成分析、人群速度分析、人群变动分析等[3]。常见的分析指标包括如下几种：

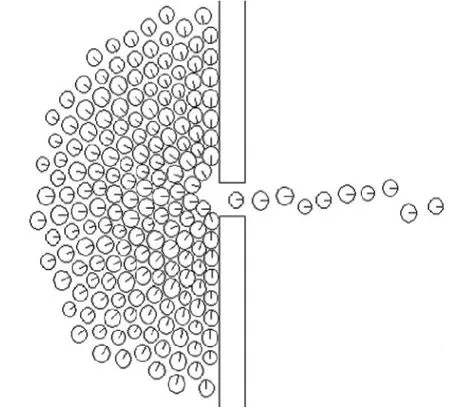
图1 拱形效应示意图

（1）人群流动规律：指人群行走时表现出来的群体运动规律。

（2）人群速度：指某群人在某段时间内的平均速度，单位是m/s。

（3）人群密度：指一个空间内人群的稠密程度，一般用单位面积上人员的数量表示，单位为人/m2；

（4）人体所占的空间：从两个涵义上表示，一个涵义是人群中个体能够占有的空间，另一个涵义是个体行走所需的空间。

（5）人流量：通过指定区域的人数。可以是平均每分钟的人流量，单位是人/min，也可以是某段时间内的人流量，单位是人。

（6）人群速度方向是指个人自由选择的行走方向，在此基础上形成的人流的速度方向，包括同向流动型、双向流动型、交叉流动型、中心聚拢型、四周发散型和散漫无序型等。

2 广州地铁的基本情况

广州地铁是广州城市轨道交通系统的重要组成部分，由广州市地下铁道总公司负责营运和管理。为了研究方便，我们选取其中的两个车站进行重点研究，其中一个是换乘车站甲，另一个是非换乘车站乙。甲车站是广州地铁的两条主要线路的换乘车站，客流量较大。该车站为地下3层结构，负1层为站厅层、负2层为设备层，负3层为站台层；甲车站共有5个出入口。乙车站为广州地铁主要干线支线上的一个重要车站，人流量一般较大。该车站为东西走向，车站分为地下2层，负1层为站厅层，负2层为站台层，站台为岛式站台，该车站有A、B、C、D共4个出入口。

3 车站人群分布特征分析

人群的年龄组成、性别组成、文化程度、职业、兴趣爱好、性格、行走目的和心理等因素的差异直接或间接影响着人群速度、人群密度、安全意识和承受拥挤的能力等，进而对人群流动规律产生影响。本节在简要介绍人群分布影响因素的基础上，对广州某地铁站内人群分布的基本情况进行进一步分析。

3.1 年龄特征对速度的影响分析

年龄通常会影响人的速度，年龄在18岁～40岁的人群运动速度明显高于60岁以上的老年人。老年人运动速度在0.6 m/s～1.2 m/s之间，相对于成年人有很大的差异；青少年运动速度与成年人速度相当；性别的差异也是影响人群行走速度的主要因素。有研究发现，男性的平均速度是1.4 m/s，而女性的平均速度是1.27 m/s。

3.2 广州地铁某车站的人群分布特征分析

本文选取广州某地铁车站，对站内的人群组成进行研究，主要采用二维分类的方法，按照年龄、性别将人群分为男青年、男中年、男老年以及女青年、女中年、女老年（以30岁作为中青年的分界点，以50岁作为中老年的分界点）。在收集上述6类乘客信息的同时，本文也分析并研究了不同时间段下这两类特殊人群，即携带行李和小孩的人群特征及比例变化情况。

（1）男、女乘客组成比例及变化趋势分析

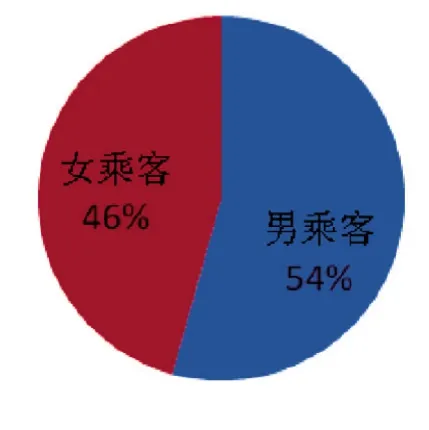
图2 男、女乘客组成比例图

从图2可以看出，男、女乘客的比例为54%∶46%，即1.2∶1，这与广州市男女比例大体相当，由此也可说明是否选择乘坐地铁和其性别无关。

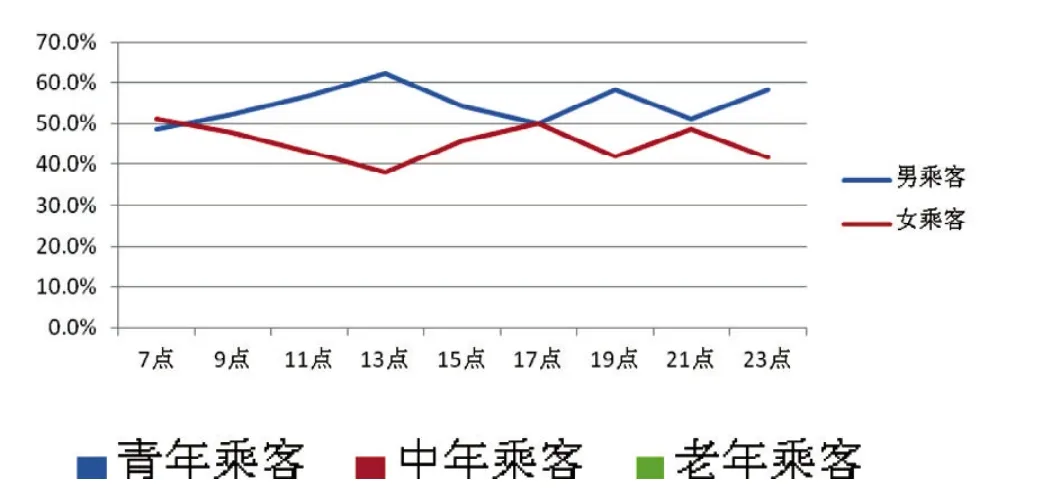
图3 男、女乘客比例变化图

从图3可以看出，男女乘客比例均在40%~60%之间波动，在13：00以及19：00处，由于男性乘客比例较大，其人群的行走速度也会出现峰值，此处应加强安全管理，以防事故发生。

图4 老、中、青乘客组成比例图

（2）老、中、青乘客组成比例及变化趋势分析

从图4可以看出，乘坐地铁的乘客中，青年乘客的比例最大，达到71%，老年乘客较少。这与地铁的出行目的有关，该换乘车站的乘客以年轻的上班族为主，中年乘客一般倾向于选择自驾车或乘坐出租车，而老年乘客则倾向于步行或乘坐公交车。

图5 老、中、青乘客比例变化图

从图5可以看出，青年乘客比例在60%~90%之间变动，在上午9：00、13：00、17：00以及23：00处达到峰值，这是由于9：00和17：00年轻乘客上下班居多，13：00属于大部分公司午间休息，23：00为广州市夜生活时间，年轻乘客活动较为频繁，人群速度在这几个时间点达到峰值。

（3）携带行李乘客所占比例及变化趋势分析

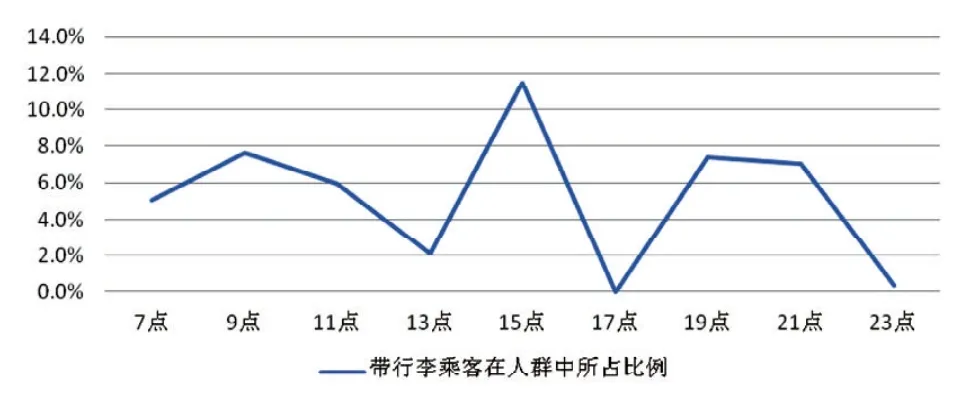
图6 携带行李乘客在人群中比例变化图

从图6可以看出，携带行李乘客比例从7：00开始上升，到9：00达到第一个峰值，然后持续下降至13：00，然后急剧上升，在15：00达到全天内最高值，占人群比例为11%左右，后持续下降至17：00，接着上升至另一个峰值，到23：00接近0。

（4）携带小孩乘客所占比例及变化趋势分析

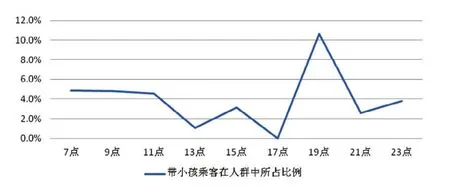
图7 携带小孩乘客在人群中比例变化图

从图7可以看出，携带小孩乘客比例从7：00到11：00处于较平稳的状态，从11：00之后开始下降，并在13：00达到第一个低谷，后继续上升至下午15：00，而后下降至0，接着持续上升至一天内最高点，达到人群总数的10%，从峰值下降至21：00后又略微上升。

4 车站人群流动因素分析

地铁站内的人群流动内容主要包括：人群的进出站流量，换乘人流量和人群速度等。各类人群流动都具有一定的规律性，且受到多种因素的影响。本文将分别选取广州地铁甲车站和乙车站的数据，对人群流量特征和人群速度特征进行分析。

4.1 人群流量特征分析

通过选取乙站的轧机数据，对车站全年和重大节假日期间的进出站流量、日均客流量和典型月份进出站流量进行对比分析，得出不同假期的人群高峰日和低峰日以及其他人群流量规律。此外，本文将2011年7月1日和2日的人流量数据作为样本，得出工作日和周末换乘通道的人流量变化规律。

4.1.1 单日人群流量分析

根据广州地铁提供的数据，本报告主要考虑4个单日的人群流量分析，分别为2010年10月1日、11月12日及12月24日，都为节日或大型体育赛事日。考虑到12月24日是周五，虽为西方节日圣诞节，但对各企事业单位仍为工作日，可以用其近似表示平时工作日乙站的人群流量。

（1）12月24日（工作日）的数据是选取当日从00：00：00～23：59：59每15 min的83组数据，用这些数据近似表示工作日期间，该站的进出站人群流量变化趋势。此外，鉴于某一时间段内，进出站人流量的差值可以反映每15 min的站内人数，如图8。

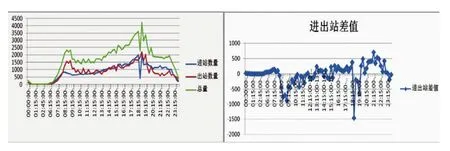
图8 工作日进出站流量、总量及其差值的变化趋势

图8表示，在6：00之前，乙站的进出站人群流量为全天最低，几乎为零。7：00～9：00以及17：00～19：00，该站的进出站流量和总流量分别出现两个峰值，总流量分别达到2 339和4 233，是人群流量需要重点疏散的时段。

（2）分析“十一”假期该站人群流量变化趋势，选取2010年10月1日的数据作为样本进行分析，具体包括当日24：00中每15 min的79组数据。将上述数据进行筛选、整理和分析后，以折线图的形式表示“十一”假期首日进出站流量和总量差值的变化趋势，如图9。

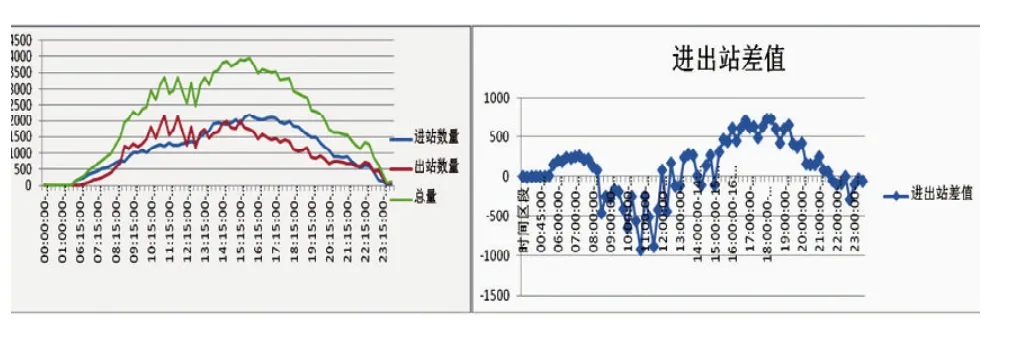
图9 “十一”假期首日进出站流量、总量及其差值的变化趋势

如图9，“十一”假期首日6：00之前，乙站的进出站人群流量是全天最低。各条曲线的变化趋势显示，上午的出站流量大于进站流量，下午和傍晚的进站流量大于出站流量，白天的进出站流量一直居高不下，不存在由于上下班带来的进出站数量的明显差异。

（3）广州亚运会期间乙站的日进出站流量可以反映大型活动对广州地铁人流量的影响。通过选取11月12日亚运会首日的数据作为样本，具体包括当日每15 min取样的89组数据。将上述数据进行筛选、整理和分析后，以折线图的形式表示亚运会首日乙站的进出站流量和总量差值的变化趋势，如图10。

图1 0 广州亚运会首日进出站流量、总量及其差值的变化趋势

如图10，该站的进出站流量在凌晨0：00出现一个小高峰，考虑到实际情况，可能是因为亚运会期间各国人不同的生活习惯。11月12日白天的客流量从9：00～19：00一直较高，对比亚运会期间体育赛事的日程，可以发现其内部的深层次关系和规律。此外，全天进出站总流量的最大值出现在下午15：00左右。进出站差值曲线表示乙站内和站台上全天的乘客人数断断续续出现最大值和最小值。

（4）考虑到选取的数据包括工作日、国庆节、春节以及大型体育赛事，本文将4天的进出站数据进行对比分析。由于原始数据存在丢失，将每天的数据进行对比和筛选，最终得出75组数据。图11反映了该站在不同情况下，每日的进出站人群流量的变化趋势对比。

图11 单日进出站总量变化趋势的对比分析

图11反映了乙站在国庆节期间的人群流量比其他3日的流量高，春节期间的客流量比其他3日的流量低。该站的人群流量在工作日期间存在明显的早高峰和晚高峰现象，其早高峰时段为上午7：00～9：00，晚高峰时段为下午1：00～19：00。此外，在大型体育赛事期间，上述组图还反映该站白天的客流量变化趋势不明显。

4.1.2 节假日期间人群流量分析

上节以折线图的形式反映该站4个特定日期的单日进出站人群流量变化趋势。本节将重点考虑国庆假期、春节以及广州亚运会期间的单日人流总量变化趋势，如图12和图13。

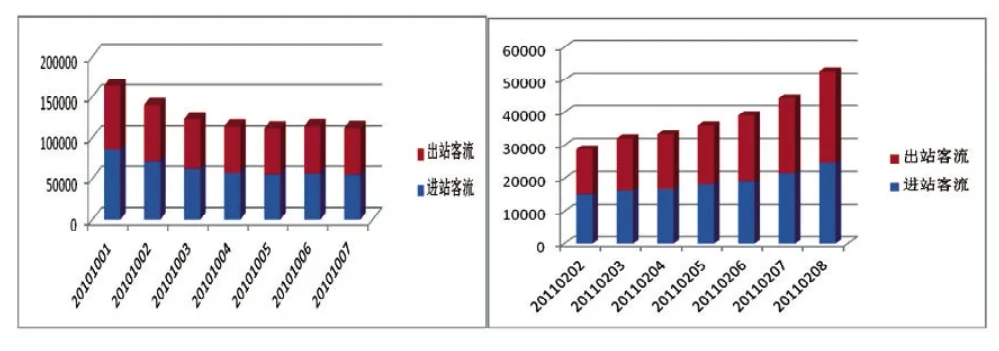
图1 2 国庆和春节期间的单日人流量对比分析

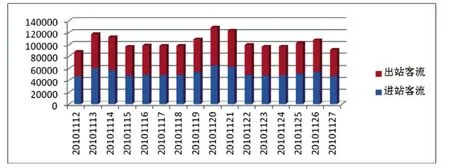
图1 3 广州亚运会期间的单日人流量对比分析

图12表示“十一”假期的单日客流高峰出现在假期首日，进出站总流量约为163 578，客流量呈逐日递减的趋势；春节期间的单日客流高峰出现在春节假期的最后一天，且单日人流量相差较大。亚运会期间的单日客流量对比分析柱形图（图13）反映出赛事首日的开幕式和末日的闭幕式并非客流量的高峰日，大部分市民可能在家看直播。

4.2 人群速度特征分析

人群速度通常是指人群整体表现出来的速度状态，它不是由单个人的速度决定的，而是人群在行走过程中互相影响和制约表现出来的一种平均速度状态。本文将地铁站内的人群速度分为平地速度和上下楼梯速度，并分别对其影响因素进行分析。

4.2.1 平地速度分析

人群速度大小是表征移动快慢的物理量。一般来说，人员密度越大，整体移动速度越慢。图14显示广州地铁某车站内，不同人群平地行走的平均速度。由于男女在身高等方面的差异，行走时的步长和步频不同，行走速度也有一定的差异。

图14 地铁内不同人群的平均速度比较图

4.2.2 上下楼梯速度分析

对各类人群在不同密集程度下的上下楼速度进行分析，在充分考虑换乘线路的情况下，对非密集区域的上下楼梯速度进行分析。

通过对视频记录中的人群上下楼梯情况进行分类和数据提取，将上下楼梯的人群对象分为男老年、男青年、男中年、女老年、女青年、女中年和小朋友7类，并将各类人群的上下楼速度进行统计分析，得出各类人群在不同密集程度下的上下楼梯速度情况，可以总结如下规律：

（1）在上下楼梯和密集程度相同的情况下，男中青年的上下楼梯速度最快，其次是女中青年，最慢的是老年人和小朋友。

（2）各类人群的下楼速度明显高于上楼速度，如在非密集区，男中年的下楼速度为3.09 n/s（n表示行人步行的步数），上楼速度为1.95 n/s。

（3）在上下楼情况相同的情况下，各类人群在非密集区的速度相差较大，如在非密集区，男青年的下楼速度为3.46 n/s，男老年的下楼速度为1.29 n/s，在密集区，男青年的下楼速度为1.85 n/s，男老年的下楼速度为1.77 n/s。

同时，本文分析男性中青年上下楼梯速度的分布情况。选取男性中青年在非密集区的下楼梯速度作为样本，分析人群上下楼梯速度的分布情况，检验这些数据是否近似服从正态分布，检验结果如图15。图15的正态P-P图进一步表明，男性中青年下楼梯速度的分布近似服从正态分布。

5 结束语

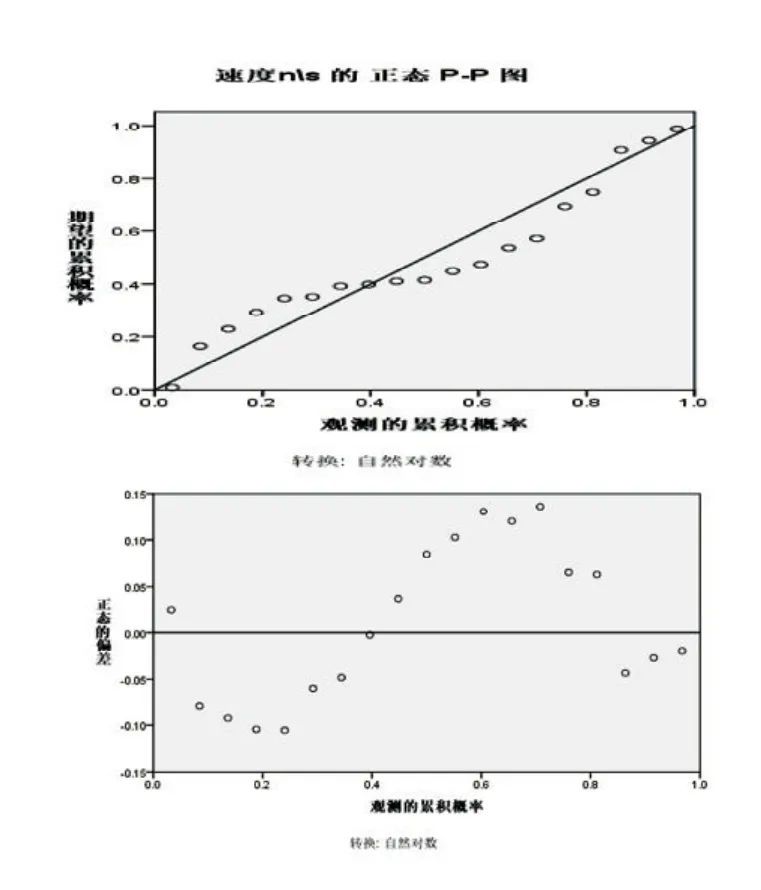
图15 速度n/s的（趋降）正态P-P图

本文研究表明，在工作日或节假日期间，地铁站内的人群组成或人群流动呈现一定的规律性。例如，工作日期间的地铁站以青年乘客为主，存在明显的早高峰和晚高峰时段，且晚高峰的持续时间大于早高峰；大型体育赛事会导致日均客流量的增多，但十一或春节期间的日均客流量相对较少，甚至低于全年日均客流量。此外，各类人群在平地、上楼梯和下楼梯等情况下，分别具有不同的速度，且存在小孩或老年人的人群速度主要受某几个小孩或老年人的影响。下一步的研究可以从以下几个方面考虑：（1）通过总结影响人群组成和人群流动的各因素，进一步分析它们之间的交互关系，并从微观层面上对人群流动规律进行研究。（2）将地铁站内的人群流动规律和相应的拥挤踩踏事件进行有效结合，并对其发生、发展和演化机理进行进一步的总结。

[1] 王理达. 地铁车站人群疏散行为仿真研究[D]. 北京：北京交通大学，2007.

[2] Daniel R. Parisi, Marcelo Gilman, Herman Moldovan. A modification of the Social Force Model can reproduce experimental data of pedestrian flows in normal conditions[J]. Physica A:Statistical Mechanics and its Applications, Volume 388, Issue 17, 1 September 2009, Pages 3600-3608

[3] David Marcozzi, Ziad A Memish.Crowd and environmental management during mass gatherings[J].The Lancet Infectious Diseases, Volume 12, Issue 2, February 2012, Pages 150-156

[4] 徐 方，魏 东. 公众聚集场所人群疏散基础数据的分析[J]. 中国安全科学学报，2008 （4）：137-145.