钢筋混凝土简支T梁桥加固后的体系时变可靠度

金 浩，梁慧超，梁 栋，齐晓丽

(1. 河北工业大学管理学院，天津 300401；2. 河北工业大学社会科学部，天津 300401；3. 河北工业大学土木工程学院，天津 300401)

近年来，人们越来越多地将时变可靠度作为一个重要参数广泛地应用于桥梁结构性能的退化分析中，但现行的设计规范[1]都是基于时不变结构可靠度理论的．如果将退化结构的抗力和功能函数看成非平稳随机过程，相应问题则成为时变可靠度问题[2]．随着我国桥梁数目增加以及老化日趋严重，桥梁的维修加固作业越来越多．对桥梁进行维修加固可以及时弥补桥梁存在的缺陷、蜕化和损伤，使桥梁安全地工作．加固后的桥梁在大气环境下，由于混凝土碳化和钢筋锈蚀，钢筋混凝土结构的性能会继续逐步劣化．但是如何评价桥梁的维修加固效果，特别是加固后桥梁结构的耐久性，仍然是一个急需解决的现实问题．

目前，单片梁(构件)的可靠度问题已经得到了比较充分的研究[3-4]．结构可靠度[1]是指结构在规定的时间内，在规定的条件下，完成预定功能的概率，一般以 ps来表示；失效概率则可表示为 pf＝1-ps．为了便于应用，定义β为可靠指标，β与 pf之间的对应关系具有唯一性．实际计算中，常以β作为结构可靠度的标准．目前，在分析桥梁结构可靠度时，通常认为其抗力R和作用效应S是与时间t无关的随机变量，也就是桥梁结构在单位时间内的失效概率不随时间变化．如果桥梁的抗力 R(t)随时间明显衰减，且其外荷载S(t)在寿命期内也可能随时间变化，则其单位时间内的可靠度也随时间变化，这即是时变可靠度的概念．

本文以目前工程中应用广泛的简支 T梁桥为研究对象，针对一般大气环境的腐蚀作用，综合考虑混凝土与钢筋性能退化的时变因素；对比分析选用不同加固方法对其加固后，其上部结构体系的时变可靠度．研究结果对预测加固桥梁结构的剩余使用寿命和维修优化决策具有重要的指导意义，同时也对其他普通钢筋混凝土梁桥，如空心板梁桥等类似桥梁的维修加固工程具有借鉴意义．

1 普通钢筋混凝土T梁的正截面抗弯承载力及其统计参数

对于普通钢筋混凝土简支梁，其正截面受弯承载力是主要的承载能力指标．因此，本文以正截面受弯承载力作为计算时变可靠度的变量，针对目前工程中常用的普通钢筋混凝土 T梁(以第 1类 T形截面为例，见图 1(a))进行研究，其截面受压区高度 x和正截面抗弯承载力Msu分别为

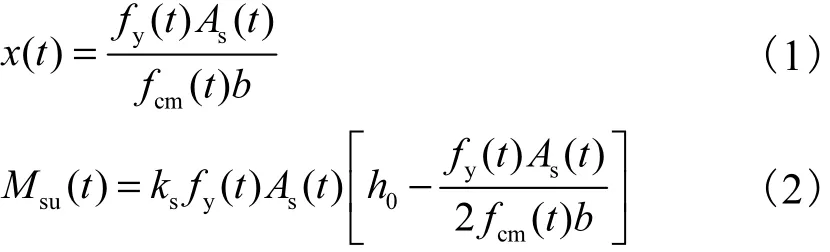
式中：fy(t)为钢筋强度的时变值；As(t)为钢筋面积的时变值；fcm(t)为混凝土弯曲抗压强度的时变值，一般取 fcm(t)＝0.737,fcu(t)，fcu(t)为混凝土立方体抗压强度的时变值；ks为钢筋与混凝土的黏结系数；h0和 b为截面有效高度和截面宽度；Msu(t)为受到腐蚀后的T梁正截面抗弯承载力．

根据现有研究成果[1]，普通钢筋混凝土T梁的抗力分布概型可视为正态分布．由误差传递公式，可以分别求出抗力Msu的均值和标准差为

式中：μ为下标参量的均值；σ为下标参量的标准差；在计算中取μfcm(t)=0.737μfcu(t)，σfcm(t)=0.737σfcu(t).

图1 T形截面受弯构件正截面承载力计算示意Fig.1 Flexural capacity calculation diagram of T-girder normal section

2 体外预应力加固T梁的可靠度

2.1 体外预应力加固T梁的正截面抗弯承载力的统计参数

利用体外预应力加固上述普通钢筋混凝土 T梁的计算示意如图 1(b)所示，其正截面抗弯承载力可按一般钢筋混凝土受弯构件的公式[5]推导出来．截面受压区高度及正截面抗弯承载力的计算公式分别为

式中：σpu(t)为构件达到承载能力极限状态时，体外预应力钢筋的拉应力；Ap(t)为体外预应力钢筋的截面面积；t1为从该桥投入营运开始计算的时间；t2为从体外预应力加固完成时刻开始计算的时间．

根据现有研究成果[1]，普通钢筋混凝土T梁加固后的抗力分布概型仍可视为正态分布，由误差传递公式，可以求出加固后的抗力均值和标准差分别为

利用相似方法可以得到增大截面加固 T梁、粘贴碳纤维布加固T梁和粘贴钢板加固T梁的正截面抗弯承载能力及其统计参数，在此不再赘述．

2.2 荷载的统计参数及分布概型

桥梁结构所承受荷载的复杂性主要体现在可变作用(汽车荷载)上，在进行结构可靠度分析时一般将桥梁结构所受的外荷载分为永久作用、可变作用和偶然作用[6]．

2.2.1 永久作用

根据现有的研究成果[1]，永久作用中随机变量的分布类型均可视为正态分布．如现浇混凝土容重的偏差系数和变异系数分别为1.04和0.06；普通钢筋容重的偏差系数和变异系数分别为1.02和0.05；桥面铺装容重的偏差系数和变异系数分别为1.00和0.04．

2.2.2 可变作用

在此主要讨论可变作用中的汽车荷载，直接采用文献[1]和文献[7]的结果：汽车荷载效应的分布形式服从极值 I型分布，利用 0.95分位值处的荷载效应可计算得到车道荷载中均布荷载qk和集中荷载Pk的偏差系数和变异系数分别为0.86和0.08．

2.3 体外预应力加固T梁的功能函数

在计算公路桥涵的承载能力极限状态的可靠度时，一般只考虑荷载的基本组合，即永久作用(主要是自重)与一种可变作用(主要是汽车荷载)，并以此作为确定结构目标可靠指标的基础．设结构的自重效应为G，汽车荷载效应为Q(t)，则在基本组合下钢筋混凝土T梁承载能力极限状态的功能函数[8]为式中 R(t)为钢筋混凝土 T梁的抗力随机过程．则设计基准期T内的失效概率为

3 普通钢筋混凝土简支梁桥上部结构体系可靠度的计算

本文假定普通钢筋混凝土简支 T梁桥的破坏形态为：当简支梁桥的某一片梁由于承载力不足而破坏时，就认为整个桥梁不再具备承载能力．因此，在计算简支梁桥的失效概率时，可将其视为串联结构体系[9]．由于系统或多或少存在着冗余，因此用纯串联模型来计算整桥上部结构的可靠度，将得到偏安全的可靠度下限．设Ej表示第j片梁的失效事件，则普通钢筋混凝土简支T梁桥上部结构的失效事件为

相应的上部结构体系失效概率为

现以Si(i＝1，2，…，n)表示简支T梁桥中第i片梁不破坏的可靠事件，以 Fi(i＝1，2，…，n)表示第 i片梁承载力不足的失效事件．为简单起见，同时不失一般性，以 5片 T梁组成的单跨简支梁桥为例计算其结构体系失效概率，推导过程中假定各失效模式相互独立，于是可得出该结构体系共有25＝32种工况.

当所有T梁都不失效时，整个桥梁的上部结构体系具备承载能力，因此该结构体系的可靠度可表示为

该体系的失效概率，也就是5片梁中任意片数出现失效情况的概率，可写为

由此，可算出整个简支梁桥上部结构体系的可靠度．

4 普通钢筋混凝土简支 T梁桥上部结构体系可靠度的算例

本文以工程中常用的简支 T梁桥[10]为例来进行上部结构体系可靠度的计算．全桥上部结构由5片T梁组成，计算跨径为 19.8,m，其截面尺寸及钢筋布置如图2所示．

图2 T梁截面尺寸及钢筋布置(单位：cm)Fig.2 Cross section of T-girder(unit：cm)

在分析过程中，设定一般大气环境，混凝土碳化腐蚀模型选用考虑环境条件和混凝土质量影响的双系数碳化预测模型[11]，即

式中：μX(t)为碳化深度的平均值；t为简支 T梁的服役时间；Ke为环境条件影响系数；Kc为混凝土质量影响系数．

本文假定混凝土保护层胀裂后的钢筋锈蚀速率不变．混凝土保护层开裂前和开裂后的钢筋锈蚀速率[12]λe1与λe2分别为

式中：kcr为钢筋位置修正系数；kce为小环境条件修正系数；X为保护层厚度；RH为环境湿度；fc为混凝土立方体抗压强度．

钢筋锈胀导致混凝土保护层开裂时间tcrk选用牛荻涛[11]的退化模型，即

式中δcr为混凝土保护层锈胀开裂时的钢筋锈蚀深度.

碳化情况下第j根锈蚀受拉钢筋的时变直径[12]为

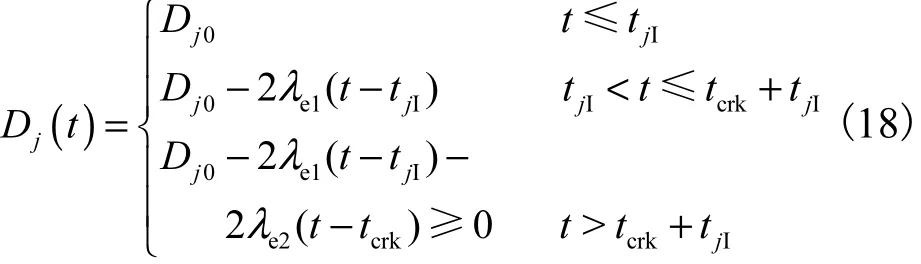
式中：Dj0为第j根钢筋初始截面积；tjI为碳化条件下第j根钢筋锈蚀开始的时间．

4.1 计算程序

确定了式(9)所示的功能函数后，可根据结构时变可靠度理论计算可靠指标β(t)．对于加固后的普通钢筋混凝土简支 T梁桥而言，涉及的随机变量较多，且变量间存在着统计相关性，故不可能得到解析解．而蒙特卡罗模拟法在处理这一类问题方面具有明显的优势．本文采用自适应重要性抽样法[13]计算普通钢筋混凝土梁桥在加固前、后的抗弯时变可靠度．

自适应重要性抽样法是通过抽样样本函数值自动搜索近似的验算点，如果功能函数 Z(t)＜0，则取Z(t)的概率密度函数最大的点为验算点 x*，如果Z(t)＞0，则取 Z(t)的概率密度函数最小值所相应的样本点为验算点 x**，通过循环确定最终近似验算点．以该验算点为抽样重心，标准差与原分布标准相同，可大幅度减少计算工作量．

根据上述计算理论，本文编制了普通钢筋混凝土简支T梁桥上部结构加固前后的体系时变可靠度计 算程序，程序框图如图3所示．

图3 简支T梁桥上部结构体系时变可靠度计算程序示意Fig.3 Flow chart for calculating the time-varying reliability of simple T-girder bridge

4.2 普通钢筋混凝土简支梁桥上部结构体系可靠度的算例

根据现行规范[1]的规定，对于结构安全等级为二级的结构，按持久状况进行承载能力极限状态设计时，公路桥梁结构的目标可靠指标β0＝4.2．

利用上述程序对普通钢筋混凝土 T梁桥上部结构体系的时变可靠度进行了计算，结果如图4所示．

图4中，不进行加固的上部结构体系时变可靠度如图中 E线所示．由于混凝土碳化和钢筋锈蚀的影响，在建成后的 27.8,a时，该桥上部结构体系的可靠度将降低至目标可靠度以下，于是该桥不能满足安全性的要求，因此在第 26年进行了加固维修，结构抗力随之大幅提升．在随后的运营过程中，其上部结构的抗力随时间而再次降低，可靠指标随时间推移也随之降低．采用不同加固方法加固后的上部结构体系时变可靠度如图4中的A～D所示，A为采用增大截面加固法，B为采用体外预应力加固法，C为粘贴碳纤维布加固法，D为粘贴钢板加固法．

图4 上部结构体系的时变可靠度Fig.4 Time-varying reliability of simple T-girder bridge

不同加固方法对结构抗力的影响不同．在再次达到目标可靠指标β0＝4.2以前，体外预应力加固法使结构抗力提升的最多；增大截面法次之；粘贴钢板法再次之，而粘贴碳纤维布法对提高可靠指标的效果最差．从长期运营的角度来看，采用体外预应力加固后的可靠指标降低的速率最小，这主要是由于该加固方法属于主动加固，改变了结构的受力体系．其次是增大截面法，采用该方法加固后，其可靠指标再次降低的速率与加固前完全相同．而其他 2种方法加固后，桥梁可靠指标降低的速率都比较快，这是由于钢板易腐蚀，黏结剂易老化等原因造成的．

5 结 论

(1) 时变可靠度作为一种理论工具为合理、准确地评估桥梁结构的初始性能和加固后性能随时间的变化提供了有效途径．

(2) 用不同加固方法对桥梁上部结构体系加固后，其可靠指标会立即明显提高，特别是体外预应力加固后，可靠指标上升的幅度最大．而采用粘贴碳纤维布加固后的可靠指标上升幅度最小，这主要是由于该方法不能提高主梁结构刚度的原因．

(3) 加固完成后，桥梁可靠指标会随着运营时间的增长而再次降低，但不同加固方法所对应的下降速率不同，其中体外预应力加固后桥梁在运营过程中可靠指标再次降低的速率最小，即在现有车辆荷载条件下，其使用寿命将最长．

［1］中华人民共和国住房和城乡建设部. GB/T 50283—1999 公路工程结构可靠度设计统一标准[S]. 北京：中国建筑工业出版社，1999.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB/T 50283—1999 Unified Standard for Reliability Design of Highway Engineering Structures[S]. Beijing：China Architecture &Building Press，1999(in Chinese).

［2］秦 权，杨小刚. 退化结构时变可靠度分析[J]. 清华大学学报：自然科学版，2005，45(6)：733-736

Qin Quan，Yang Xiaogang. Time-dependent reliability of deteriorating structures [J].Journal of Tsinghua University：Science and Technology，2005，45(6)：733-736(in Chinese).

［3］Ellingwood R M. Reliability based service-life assessment of aging concrete structures [J].Journal of Structural Engineering，1993，119(5)：1600-1621.

［4］Stewart M G，Rosowsky D V. Time-dependent reliability of deteriorating reinforced concrete bridge decks [J].Structural Safety，1998，20(1)：91-109.

［5］中交第一公路勘察设计研究院有限公司. JTG/T J22—2008 公路桥梁加固设计规范[S]. 北京：人民交通出版社，2008.

First Highway Survey and Design Institute Company Limite. JTG/T J22—2008 Code for Reinforcement of Highway Bridge[S]. Beijing：China Communications Press，2008(in Chinese).

［6］中华人民共和国交通运输部. JTG D60—2004 公路桥涵设计通用规范[S]. 北京：人民交通出版社，2004.Ministry of Transport of the People’s Republic of China.

JTG D60—2004 General Specifications for Design of Highway Bridges and Culverts[S]. Beijing：China Communications Press，2004(in Chinese).

［7］中华人民共和国交通运输部. JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京：人民交通出版社，2004.

Ministry of Transport of the People’s Republic of China.JTG D62—2004 Code for Design Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. Beijing：China Communications Press，2004(in Chinese).

［8］贡金鑫，赵国藩. 考虑抗力随时间变化的结构可靠度分析[J]. 建筑结构学报，1998，19(5)：43-51.

Gong Jinxin，Zhao Guofan. Reliability analysis of deteriorating structures considering time-variant resistance[J].Journal of Building Structures，1998，19(5)：43-51(in Chinese).

［9］李桂青. 结构可靠度[M]. 武汉：武汉工业大学出版社，1989.

Li Guiqing.Reliability of Structure[M]. Wuhan：Wuhan University of Technology Press，1989(in Chinese).

［10］叶见曙. 结构设计原理[M]. 北京：人民交通出版社，2005.

Ye Jianshu.Concrete Structures Design Tenets[M].Beijing：China Communications Press，2005(in Chinese).

［11］牛荻涛. 混凝土结构耐久性与寿命预测[M]. 北京：科学出版社，2003．

Niu Ditao.Durability And Life Forecast of ReinforcedConcrete Structure [M]. Beijing：Science Press，2003(in Chinese).

［12］王建秀，秦 权. 考虑氯离子侵蚀与混凝土碳化的公路桥梁时变可靠度分析[J]. 工程力学，2007，24(7)：86-93．

Wang Jianxiu，Qin Quan. Analysis of time-dependent reliability of RC highway bridges considering chloride attack and concrete carbonation [J].Engineering Mechanics，2007，24(7)：86-93(in Chinese).

［13］Pulidoe Jocobs T L，Prates Delima E C. Structural reliability using Monte-Carlo simulation with variance reduction techniques on elastic-plastic structures [J].Computers and Structures，1992，43(3)：419-430.