降雨入渗条件下边坡湿陷变形的数值模拟

王柳江，刘斯宏，李 卓，白福清

(河海大学水利水电学院，南京 210098)

降雨入渗是引起边坡产生滑动破坏的主要因素之一，且非饱和土边坡的变形和稳定也一直是岩土工程界研究的热点和难点之一．由于我国分布有广泛的土质边坡，每年降雨引起的滑坡都对国家造成了重大的经济损失和人员伤亡．因此，深入研究降雨引起斜坡失稳的规律并建立定量的分析模型对于滑坡的预防有重要的指导意义．

目前，研究降雨入渗对边坡稳定性影响的手段主要有 2类：①采用原位监测，通过采集大量的监测数据建立相应的统计模型；②建立系统的数学物理计算模型对降雨入渗下的边坡进行定量分析．迄今为止，人们主要采用第 2种方法对边坡稳定性进行分析．其中，通过渗流计算和极限强度平衡法相结合分析降雨入渗下边坡稳定性的方法被广泛使用[1-4]，然而该法通常根据非饱和土的强度特性来反映边坡的失稳机制而更能直观反映边坡失稳的变形规律却无法得到．由于降雨入渗下的边坡变形实质上是典型的非饱和土固结问题，因此，它的解决必须基于非饱和土的渗流和应力耦合理论[5-6]．Cho等[7]开发了水、气、固三相耦合程序，且对降雨入渗下的均质土坡进行了分析，但没有对边坡变形进行过深入研究．徐晗等[8]建立了一个考虑水力渗透系数特征曲线、土水特征曲线和修正 Mohr-Coulomb破坏准则的非饱和土流固耦合计算模型，然而所采用的非饱和土本构模型并不是真正意义上的弹塑性模型．因此，在非饱和土多孔介质力学理论的基础上采用非饱和土弹塑性模型对降雨入渗下边坡的湿陷变形进行分析具有重要意义．为了更准确地反映非饱和土的变形特性，很多学者在弹塑性理论框架内建立了非饱和土本构模型，Alonso等[9-11]提出的 BBM 模型目前已被广泛应用.但该模型也存在一些缺陷：如通过 BBM 模型中的Load-Collapse(LC)屈服函数计算得到的湿化变形随着围压的增大而增大，这与大量的试验结果不符；模型采用净应力作为应力状态变量，无法很好地反映非饱和土的水力-力学耦合特性，且在数值计算中运用困难．为此，在 BBM 模型的基础上对其修正进行建模的思路已经得到了很多学者的关注[12-13]．

笔者在非饱和土多孔介质力学理论的基础上，采用能够考虑吸力影响以及非饱和土水力-力学耦合特性的修正BBM 模型，开发相应的有限元程序，模拟了降雨入渗下边坡的湿陷变形，研究了降雨持时、降雨强度以及饱和渗透系数对边坡渗流和变形的影响．

1 非饱和土弹塑性本构模型

BBM模型最早由西班牙学者Alonso提出，该模型能通过吸力变化来反映非饱和土干湿循环下的胀缩特性．但其仅是基于特定试验结果的本构模型，尚有一些地方不够完善，例如：LC曲线在描述高围压下土体的湿化变形时与试验结果不符；模型中参考应力 pc的物理概念不明确，且当 pc等于饱和状态下土体的前期固结应力 p0*时，LC曲线在 p-s平面上为一条竖直线，此时无法反映吸力变化引起的土体塑性体应变；模型采用净应力作为应力状态变量，在描述非饱和土的饱和-非饱和状态过渡时存在困难．为了使其更好地适用于非饱和土的流固耦合分析，这里从应力状态变量、压缩线斜率和LC屈服面3方面对其进行了修正．

1.1 修正BBM模型简介

修正后的BBM模型描述如下．

屈服函数采用了修正剑桥模型的形式，即

式中：p′为平均主应力；q为广义剪应力；sp′为随吸力增大的附加黏聚力；0p′为非饱和土的前期最大固结应力，其值随吸力的变化而变化，在 p-s平面上绘制出来即为LC屈服线．

与初始BBM模型不同，本文中的LC曲线方程是在高应力状态下推导得到的，当围压增大到一定值时，所有吸力下的压缩曲线交于一点，此时土体吸力降低不引起变形，则LC曲线函数为

式中：pn为不同吸力下土体压缩曲线交点所对应的应力；p0*为饱和状态下土体的前期最大固结应力；λ( 0 )为饱和状态下土体的压缩系数；κ为土体回弹系数；s为吸力；pat为大气压；κs为围压等于 1,MPa时土体干化或湿化时由吸力变化引起的体积压缩系数；λ( s )为非饱和状态下吸力等于 s时对应的土体压缩曲线斜率．根据Sun等[14]试验结果可知在高围压下，非饱和土体的压缩曲线斜率随吸力的增大而增大，其关系式为

式中λs为试验参数，由吸力趋向于无穷大时的土体压缩曲线斜率与吸力等于 0时的土体压缩曲线斜率相减即可得到．图1为根据式(2)和式(3)在p-s平面上绘制的 LC曲线，其中参数λ(0)=0.2，κ=0.03，pn= 1 MPa ，κs= 0 .002保持不变，变化参数 p0*和λs得到．

为更好地描述非饱和土模型中水力-力学的相互作用关系，使模型更适用于有限元流固耦合分析，该模型采用了平均骨架应力σi′j作为应力状态变量，即

式中：ijδ为Kronecker符号；rS为饱和度；au和wu分别为孔隙气压力和孔隙水压力，通常岩土工程中认为土体与大气相通，则孔隙气压为大气压，ua=0．

图1 不同参数下的LC曲线Fig.1 LC curves at different values of parameters p0* and λs

1.2 应力-应变关系式推导

有限元计算过程中需采用应力-应变的增量关系，因此进行有限元计算前需将屈服函数先进行变换．首先，根据相关联流动法则得到塑性应变增量为

式中Λ为比例系数，可根据屈服函数的连续性条件获得．将式(1)写成

其次，根据式(2)可得

由于塑性体应变作为硬化参数，则屈服面上塑性体应变增量相等，可采用饱和状态下土体的应力状态及其应力增量计算得到，即

然后，将式(5)代入式(8)，得

非饱和土的应力-应变增量关系可表示为

式中：De为弹性刚度矩阵；We为与吸力对应的弹性刚度向量；dεe为弹性应变增量，可表示为

将式(9)代入式(7)后再代入式(6)，同样，将式(11)代入式(10)后再代入式(6)，即可得到比例系数Λ，即

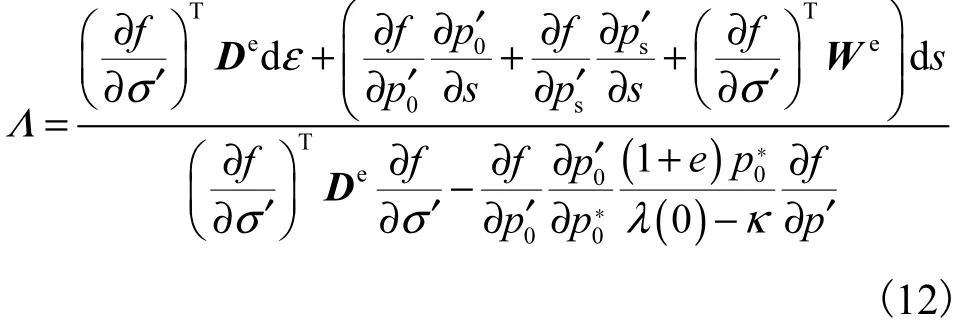
将式(12)代入式(11)，然后联合式(10)，移项后得到土体的弹塑性应力-应变增量表达式为

2 计算原理

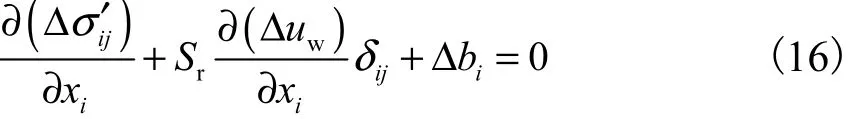
式中：Δσi′j为平均骨架应力张量的增量；xi为坐标；Δuw为孔隙水压力增量；Δbi为体力增量．

非饱和孔隙水连续方程为

2.1 非饱和土固结理论数学模型

在忽略温度的影响以及假设土体与大气相通的条件下，根据非饱和土多孔介质理论，非饱和土固结方程由土骨架应力平衡微分方程和非饱和土孔隙水连续流动方程组成．

土骨架的应力平衡微分方程为

式中：n为孔隙率；Kw为水的体积压缩模量；h为水头；C ( s)为容水度，C =∂θw∂s，θw为体积含水量；εii为土骨架单元体应变；kisj为饱和渗透系数张量；kr( s)为相对渗透系数；γw为水的容重．

2.2 土-水特征曲线模型

土体土-水特征曲线指基质吸力和饱和度之间的关系，代表土体孔隙系统的持水特性．下文对文献[15]中的边坡进行数值模拟，根据土-水特征实测值曲线拟合情况，其结果与文献[7]介绍的土-水特征曲线模型一致，则本文采用的饱和度与吸力之间的关系为

式中：Sre为残余水饱和度；Sm为最大饱和度；as、bs和 cs为参数．下文计算中土体水力渗透系数与吸力之间也满足文献[7]中的水力渗透特性曲线函数，即

式中：rk为相对渗透系数；aw、bw和 cw为拟合参数．图 2(a)和(b)为文献[15]中土-水特征及水力渗透系数的实测值采用式(18)和式(19)的拟合情况．

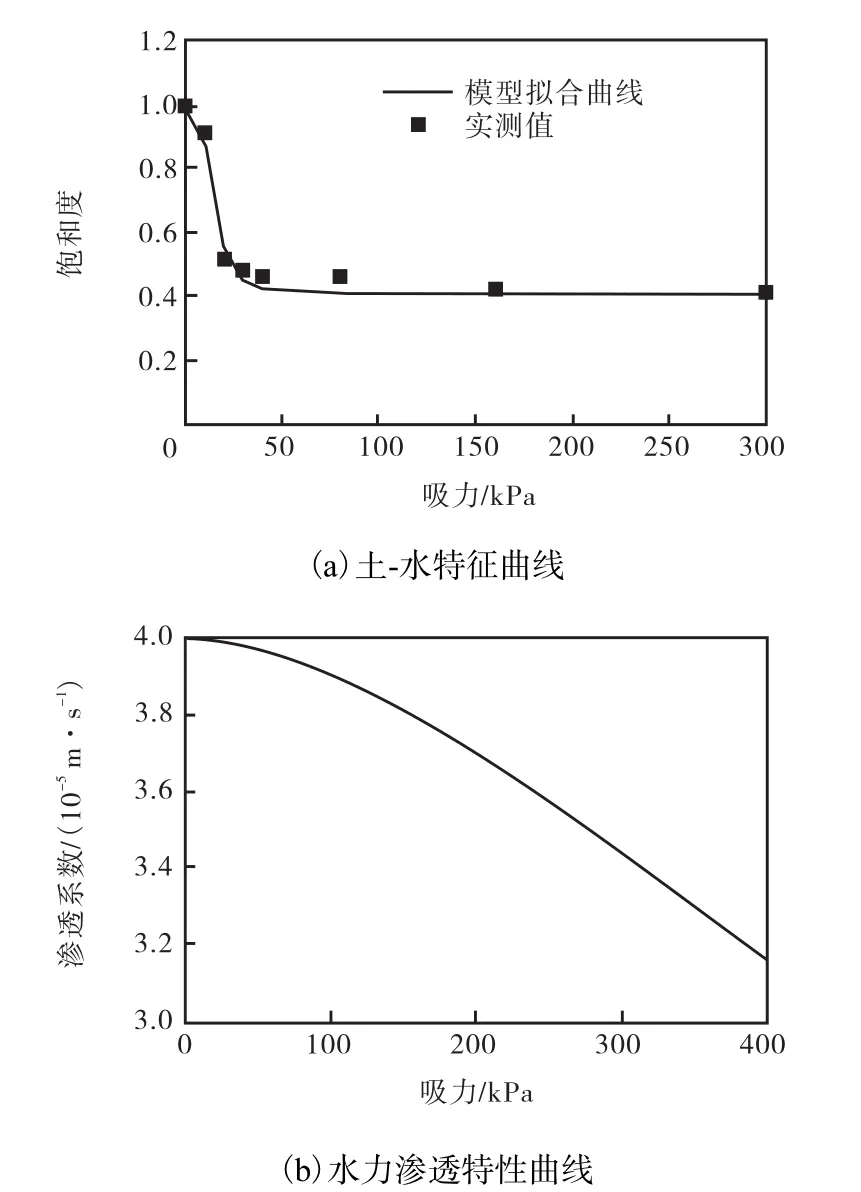
图2 土-水特征曲线和水力渗透特性曲线Fig.2 Soil-water characteristic curve and hydraulic conductivity characteristic curve

3 边坡降雨入渗变形的有限元模拟

为研究降雨入渗下非饱和土边坡的变形特性，根据上文介绍的计算原理和应力-应变本构关系，开发了有限元计算程序，对一降雨边坡进行了数值模拟[15]．

3.1 有限元计算模型及条件参数

图3为原型边坡断面的有限元网格，图中黑点代表监测点，在计算结果分析中应用．其中 a～e在坡面以下 5～10,m，而 f和 g分布较深，在坡面以下50～100,m．其边界条件如下：底边界为位移固定和不透水边界；左右两侧为水平向位移约束及零流量边界；边坡表面为降雨入渗边界，入渗量的确定将在下节介绍．初始条件包括初始应力和初始孔压，其中初始应力根据边坡自重确定，而初始孔压的确定采用如下方法：设定右侧水位为350,m 作为常水头边界，模拟未降雨条件下边坡渗流至稳定，将计算得到的孔压和饱和度作为初始值，图4为初始孔压分布情况．根据文献[15]论述，边坡土体为砾类土，容重γ= 1 6.7 kN/m3，孔隙比 e = 0 .62，比重 Gs= 2 .51，饱和渗透系数 ks= 4× 1 0-5m/s ，弹性模量 E = 1 0 MPa ，泊松比ν=0.3，黏聚力c′= 4 .0 kPa，内摩擦角φ′=36.9°，其中土体的土-水特征曲线及水力渗透特性曲线如图2(a)和(b)所示．由于文献[15]并未针对修正BBM模型专门进行参数测定，因此本文通过已知参数变换以及工程类比的方法近似获取修正BBM模型参数．首先，根据弹性模量E与回弹系数κ之间的关系式为

式中p为围压，通常在100～150,kPa之间．将已知参数代入式(20)即可得到κ，且κ比λ小，一般κ= ( 0 .1 ∼ 0 .2)λ，则λ可近似得到．

在p-q平面上临界状态线的斜率M可采用内摩擦角表示，即

根据工程类比的方法，其余参数参考文献[16]，则得到的修正 BBM 模型计算参数见表 1．本文共模拟了 30,h的降雨过程，平均降雨量为 1.2,m/d，在本文中将该情况设为基本工况．为研究降雨强度和土体饱和渗透系数对边坡渗流和变形的影响，本文根据基本工况，通过改变降雨强度和饱和渗透系数，分别计算了饱和渗透系数保持 4.0×10-5,m/s不变，降雨强度为0.6,m/d、1.8,m/d、2.4,m/d的情况；以及降雨强度保持 1.2,m/d不变，饱和渗透系数为 1.0× 10-5,m/s、5.0×10-6,m/s、1.0×10-6,m/s的情况．

图3 有限元计算网格及其监测点

Fig.3 FEM mesh and selected nodes for result analysis

图4 初始孔压分布等值线(单位：kPa)Fig.4 Contour of initial pore-water pressure in slope(unit：kPa)

表1 修正BBM模型参数Tab.1 Parameters of improved BBM constitutive model

3.2 降雨入渗边界的处理

降雨入渗水流在土体非饱和区是变化的，属于水分通过岩土体包气带运移的两相流问题，且雨水入渗量通常受降雨强度、降雨持时、岩土初始含水量以及入渗面几何特征等因素的影响，因此降雨入渗是一个复杂的边界非线性渗流问题．在渗流计算中，入渗面通常简化为边界条件，当降雨强度大于入渗能力产生地表径流时，为水头边界；当降雨强度小于饱和渗透系数时，为流量边界．本文采用了以积水点为判断标准的降雨入渗计算方法[17]，其地表入渗能力通过地表水头和入渗率进行判断．当地表节点非饱和时，以地表节点为临界水头(h＝0)时的入渗量为入渗能力来判断是否由流量边界转化为水头边界；饱和时，以地表节点的入渗率为入渗能力来判断是否由水头边界转化为流量边界．

4 计算结果及其分析

图5 不同时刻水平位移分布等值线(单位：cm)Fig.5 Contours of horizontal displacement in slope at different time(unit：cm)

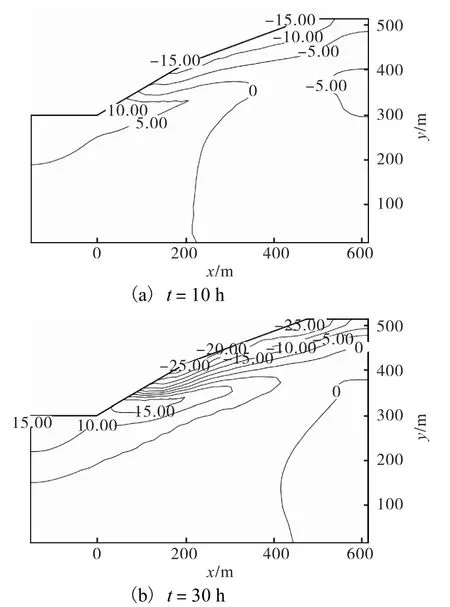
图6 不同时刻竖向位移分布等值线(单位：cm)Fig.6 Contours of vertical displacement in slope at different time(unit：cm)

图 5和图 6为不同时刻边坡水平位移和沉降等值线．由图可见，水平位移主要发生在地下水位线附近及其以上的非饱和区，其中坡脚位置土体的水平位移向右，而地下水位线以上的向左，最大值出现在边坡坡面拐角处，且边坡顺坡向的水平位移随着降雨持续而增大；同时，降雨导致了边坡内出现了沉降和隆起，沉降主要发生在地下水位以上非饱和区，而地下水位以下饱和区的竖向位移朝上．其中，沉降主要是由非饱和区吸力减小导致土体强度降低软化引起，而隆起则是由饱和区土体孔压增大导致有效应力减小而引起的土体回弹．由图可知，最大湿陷变形发生在坡顶及边坡坡面拐角处，且沉降值及隆起量均随降雨持续而增大．因此，根据边坡的变形分布可知坡面拐角和坡顶是决定该边坡稳定性的主要部位，由降雨引起的边坡滑动面极有可能贯穿这2个部位．

图7为a～g点的孔压增量随时间变化情况．由图7可知：降雨初期，a～e的孔压增量基本一致，随着降雨持续，孔压增速逐渐减小，且与位置有关，其中a、b和c的减小量依次增大，而d和e基本相同；边坡浅层b和 d的孔压增速明显大于深层土体 f和g.由此可知，上述点的孔压变化规律取决于土体所处的位置．对于边坡表层土体，由于初始吸力随高度增大而增大，在降雨条件下，吸力越低的表层土体能越快达到饱和状态，且当表层土体趋向于饱和时，由于雨水入渗率逐渐减小，则表面土体的孔压增大速度也相应减小；对于深层土体单元，由于降雨入渗是雨水由表及里流动的过程，因此，深层土体的孔压增大与消散过程较表层土体有明显的滞后性．图8为监测点塑性体应变的变化规律，而降雨30,h后的塑性剪应变等值线分布如图9所示．由图可见，表层土体单元的塑性体应变随高度的增大而减小，随着降雨的持续而增大，塑性剪应变最大值位于坡脚地下水溢出部位，说明塑性变形不仅与位置有关，还与降雨持续时间有关，且由降雨引起的边坡塑性破坏区从坡脚往坡顶方向发展．图10为 b～e在降雨过程中的应力路径方向．由图10可见，其应力路径方向朝左上方，这主要与降雨的入渗有关．可以解释如下：降雨入渗导致表层土体的孔压增大而使平均应力p′减小，同时，土体模量降低以及土体自重增大又使广义剪应力q′增大．

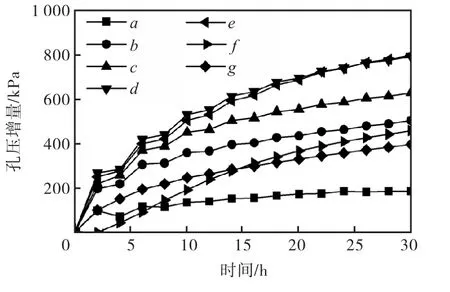
图7 监测点孔压增量与时间关系Fig.7 Pore-water pressure increments of selected nodes versus time

图8 监测点塑性体应变与时间关系Fig.8 Plastic volumetric strains of selected nodes versus time

图9 降雨结束后塑性剪应变分布等值线(单位：%)Fig.9 Contour of plastic shear strain at the end of rainfall(unit：%)

图10 监测点的应力路径Fig.10 Stress path of selected nodes

图11～图13为不同降雨强度下监测点孔压、沉降和水平位移随降雨持时的变化．由于本文计算采用的降雨强度均小于土体的饱和渗透系数(4.0×10-5,m/s)，因此雨水基本能够完全入渗．由图可知，该边坡内孔压、沉降和水平位移随降雨强度的增大而增大，且当降雨强度为 2.4,m/d时，降雨持续 30,h后，深层土体 g点出现了正孔压，且该位置土体沉降出现了回弹，这与降雨引起的地下水位上升且有效应力减小有关．

图11 不同降雨强度下监测点孔压与时间关系Fig.11 Pore-water pressure versus time with different rainfall intensity

图12 不同降雨强度下监测点沉降与时间关系Fig.12 Settlement versus time with different rainfall intensity

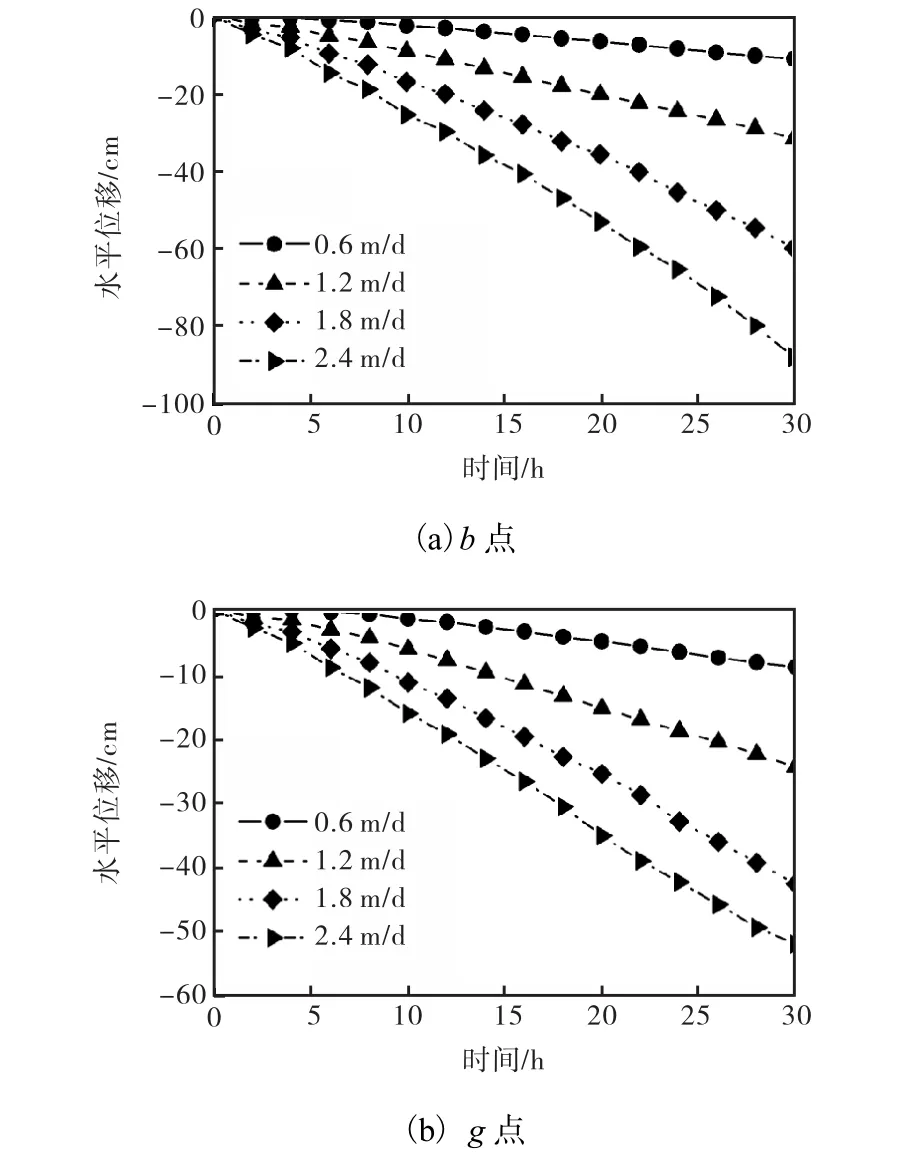
图13 不同降雨强度下监测点水平位移与时间关系Fig.13 Horizontal displacement versus time with different rainfall intensity

图14 不同饱和渗透系数时监测点孔压与时间关系Fig.14 Pore-water pressure versus time with different saturated permeability

图 14～图 16为不同饱和渗透系数时监测点孔压、沉降和水平位移随降雨持时的变化．设降雨强度保持 1.2,m/d，改变土体饱和渗透系数．结果表明饱和渗透系数对边坡内孔压和变形的影响较大．由图14可见，对于坡面浅层土体，饱和渗透系数越小，吸力降低速度越快；而深层土体则是在饱和渗透系数接近降雨强度时吸力降低速度较快，而当饱和渗透系数远大于或远小于降雨强度时，吸力减小速度较慢，该现象与降雨强度和土体渗透系数之间的关系有关．通常降雨初期边坡表层土体的入渗量等于降雨量，所以根据渗流连续性条件以及达西定律可知：当表层土体具有相同入渗量时，渗透系数越小，孔压增量越大；对于深层土体，当渗透系数远小于降雨强度时，由于入渗速度缓慢，导致孔压增速明显减慢，而当饱和渗透系数远大于降雨强度时，由于土体透水性极强，孔压消散速度同样较快，则降雨引起的孔压增量较小．由图15和图16可见，当土体的饱和渗透系数为1.0×10-5～5.0×10-6,m/s时，边坡的变形远大于饱和渗透系数为 4.0×10-5和 1.0×10-6,m/s的变形，说明当降雨强度大于且接近饱和渗透系数时，边坡发生滑动破坏的可能性较大．通过不同饱和渗透系数下的耦合计算表明：当边坡的渗透系数远大于或远小于降雨强度时，边坡失稳的可能性较小，这与边坡加固工程中设置坡内排水系统或表面隔水措施的原理相似．

图15 不同饱和渗透系数时监测点沉降与时间关系Fig.15 Settlement versus time with different saturated permeability

图16 不同饱和渗透系数时监测点水平位移与时间关系Fig.16 Horizontal displacement versus time with different saturated permeability

5 结 论

(1) 降雨入渗时，最大水平位移位于坡面拐角处，而最大湿陷变形位于坡面拐角和坡顶位置，说明坡面拐角和坡顶是决定边坡稳定性的主要部位．则在降雨过程中，这2个部位极有可能率先发生塑性破坏而诱发局部滑动，因此，对该部位进行防/排水或加固处理对边坡的稳定性具有重要意义．

(2) 降雨期间边坡内孔压的变化与土体位置有关，边坡底部孔压增量较顶部小，深层较表层小．同时，在初始应力状态接近的情况下，土体的塑性变形与初始吸力有关，初始吸力越大，塑性变形越小，且降雨引起的塑性破坏区从坡脚往坡顶发展．

(3) 在饱和渗透系数大于降雨强度的条件下，边坡内孔压和变形的发展与降雨持时和降雨强度成正比．

(4) 降雨条件下，边坡内渗流和变形的变化受土体饱和渗透系数的影响显著，当土体的饱和渗透系数小于且接近降雨强度时，边坡表层土体位移较大；而当饱和渗透系数远大于或小于降雨强度时，边坡表层土体的位移较小．

(5) 通过对该边坡实例的分析，说明了本文建立的计算模型以及开发的程序能够客观地反映非饱和土边坡在降雨入渗下的湿陷变形特性，为降雨入渗下边坡稳定性的评价及其滑坡预测提供了新的手段．

［1］吴宏伟，陈守义，庞宇威. 雨水入渗对非饱和土坡稳定性影响的参数研究[J]. 岩土力学，1999，20(1)：1-14.

Ng Wangwai Charles，Chen Shouyi，Pang Yuewai. Parametric study of effects of rain infiltration on unsaturated slopes[J].Rock and Soil Mechanics，1999，20(1)：1-14(in Chinese).

［2］Chen H，Chen R H，Yu F C，et al. The inspection of triggering mechanism for a hazardous mudflow in an urbanized territory[J].Environmental Geology，2004，45(7)：899-906.

［3］Ng C W W，Pang Y W. Influence of stress state on soilwater characteristics and slope stability[J].Journal of Geotechnical and Geoenvironmental Engineering，2000，126(2)：157-166.

［4］吴长富，朱向荣，尹小涛，等. 强降雨条件下土质边坡瞬态稳定性分析[J]. 岩土力学，2008，29(2)：386-391.

Wu Changfu，Zhu Xiangrong，Yin Xiaotao，et al.Analysis of soil slope’s transient stability under intensive rainfall[J].Rock and Soil Mechanics，2008，29(2)：386-391(in Chinese).

［5］沈珠江. 非饱和土简化固结理论及其应用[J]. 水利水运工程学报，2003(4)：1-6.

Shen Zhujiang. Simplified consolidation theory for unsaturated soils and its application [J].Hydro Science and Engineering，2003(4)：1-6(in Chinese).

［6］陈铁林，沈珠江，杨代泉. 湿陷性黄土渠道浸水变形的数值模拟[J]. 水利学报，2005，36(3)：309-313.

Chen Tielin，Shen Zhujiang，Yang Daiquan. Numerical simulation on wetting deformation of collapsible loess ditch[J].Journal of Hydraulic Engineering，2005，36(3)：309-313(in Chinese).

［7］Cho S E，Lee S R. Instability of unsaturated soil slopes due to infiltration[J].Computers and Geotechnics，2001，28(3)：185-208.

［8］徐 晗，朱以文，蔡元奇，等. 降雨入渗条件下非饱和土边坡稳定分析[J]. 岩土力学，2005，26(12)：1957-1962.

Xu Han，Zhu Yiwen，Cai Yuanqi，et al. Stability analysis of unsaturated soil slopes under rainfall infiltra tion[J].Rock and Soil Mechanics，2005，26(12)：1957-1962(in Chinese).

［9］Alonso E E，Gens A，Josa A. A constitutive model for partially saturated soils[J].Geotechnique，1990，40(3)：405-430.

［10］Bolzon G，Schrefler B A，Zienkiewicz O C. Elastoplastic soil constitutive laws generalized to partially saturated states[J].Geothecnique，1996，46(2)：279-289.

［11］Sheng Daichao，Fredlund D G，Gens A. A new modeling approach for unsaturated soils using independent stress variables[J].Can Geotech J，2008，45：511-534.

［12］Wheeler S J，Sivakumar V. An elasto-plastic critical state framework for unsaturated soils[J].Geotechnique，1995，45(1)：35-53.

［13］缪林昌. 非饱和土的本构模型研究[J]. 岩土力学，2007，28(5)：855-860.

Miao Linchang. Research of constitutive model of unsaturated soil[J].Rock and Soil Mechanics，2007，28(5)：855-860(in Chinese).

［14］Sun De’an，Sheng Daichao，Xu Yongfu. Collapse behaviour of unsaturated compacted soil with different initial densities[J].Can Geotech J，2007，44：673-686.［15］Chen R H，Chen H P，Chen K S，et al. Simulation of a slope failure induced by rainfall infiltration[J].Environmental Geology，2009，58(5)：943-952.

［16］Sun D A，Sheng D，Li X，et al. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils under undrained conditions[J].Computers and Geotechnics，2008，35(6)：845-852.

［17］朱 伟，程南军，陈学东，等. 浅谈非饱和渗流的几个基本问题[J]. 岩土工程学报，2006，28(2)：235-240.

Zhu Wei，Cheng Nanjun，Chen Xuedong，et al. Some fundamental problems of unsaturated seepage[J].Chinese Journal of Geotechnical Engineering，2006，28(2)：235-240(in Chinese).