p-Laplacian方程组大解的存在性*
印凡成,王滕滕,黄健元
(1.河海大学理学院,江苏 南京210098;2.河海大学公共管理学院,江苏 南京210098)
对椭圆型p-Laplacian方程解的研究一直是学者们感兴趣的问题,已经得到了大量深刻的结果。有关p-Laplacian方程在全空间RN上解的存在性研究,常用的方法有不动点法,变分法,上下解法,运用山路引理等。各类方法各有其特殊性和优势,同时也有其局限性。关于椭圆型p-Laplacian方程的大解,国内外许多学者已经运用不同的方法进行了研究。文献[1]运用上下解方法得到方程

的整体解。文献[2]也运用上下解方法研究非线性椭圆型方程
在光滑有界区域Ω⊆RN和整个Ω=RN空间正的边界爆破弱解的存在性。关于有界区域上单个方程形如
其中p>1,Ω⊂RN的问题,很多学者都有研究,并有所收获。尤其在文献[3]中,作者分别证明了方程在γ>p-1,Ω=RN或Ω是RN上的有界区域,以及在γ 其中m>1,λ:[0,∞)→[0,∞)是连续函数,φ:RN×[0,∞)→[0,∞)也是连续函数。同样方程组以及p(x)-Laplacian方程组问题也有很多学者进行了研究。在文献[5]中,作者考虑了下面不含梯度项的方程组 的正的整体解的存在性。文献[6]中,作者研究了下列非线性椭圆型方程组 在有界区域边界大解的存在性问题。 在上述文献中,虽然研究到非线性方程组解的问题,但涉及方程组大解问题的研究非常少。本文将依据比较原理,借鉴文献[7]中单个方程在无界区域上大解存在性问题的上下解方法,通过联立解不等式组的方式,结合具体情况,考虑上下解存在时需要满足的条件,研究如下无界区域上强耦合项的非线性椭圆型p-Laplacian方程组 大解的存在性问题。其中1 (2) (3) 定义2 方程(1)的解u(x)如果满足当x→∂Ω时,有u→∞,则称u(x)为方程(1)的大解,也称爆破解。如果Ω=RN,x→∂Ω也就是|x|→∞,这样的解u(x)称为整体大解,也称整体爆破解。 引理1[8](弱比较原理) 设Ω是RN(N≥2)上的有界区域,边界∂Ω光滑,并且θ是(0,∞)→(0,∞)的连续不减函数,设u1,u2∈W1,p(Ω),且对任意的非负函数ψ∈W1,p(Ω)满足 ▽u1▽ψθ(u1)ψdx≤ 如果在边界∂Ω有不等式u1≤u2成立,则在有界区域Ω上不等式u1≤u2也成立。 引理2[9](单个方程的上下解原理) 非线性椭圆型方程 (4) 其中指数λ∈(0,1)且f(x,u)关于u在{(x,u):x∈RN,w(x)≤x≤v(x)}是Hölder连续,则方程(4)有整体解u(x)满足w(x)≤u(x)≤v(x),x∈RN。 证明设BR是RN上半径为R的球,考虑边值问题 sup{|uR|;x∈B2}≤C3 (10) 注1 函数v(x)(或w(x))满足偏微分不等式(5)(或(6))被称为方程(4)在RN上的上解(或下解)。 引理3[5](方程组的上下解原理) 非线性椭圆型方程组 (11) ≤u(x)≤,≤v(x)≤ 证明 利用和引理2相同的证明方法,即可证得引理3。具体步骤可参见文献[5]。 本文主要研究强耦合项的非线性椭圆型方程组(1)大解的存在性问题。其中1 任意m(x),n(x)连续,且∃R0>0,m1,m2>0,n1,n2>0和α,β∈R1,使得 (12) (13) 取 ,·, 容易验证 (14) 取 λVk,μUn (15) 这里λ,μ>0为参数,n,k>0。 , (16) ≤u(x)≤,≤v(x)≤ 下面证明由(15)-(16)所定义的函数是问题(1)的上下解。取 ,, 先考虑下解的情况,当|x|≤R0时 则 ≥k 则 ≤ 即 (17) 则有 ≤ 即 ≤μq-1-e (18) 联立(17)和(18)解不等式组 解以上不等式组可得 当|x|≥R0时, ≤ 即 ≤λp-1-a (19) ≤ 即 ≤μq-1-e (20) 联立(19)和(20)解不等式组 解以上不等式组可得 类似地,对于方程组的上解可得到同样的结论。 文章探讨了无界区域上强耦合项的非线性椭圆型p-Laplacian方程组大解的存在性,并得到大解存在需要满足的条件(a-p+1)(e-q+1) 参考文献: [1]YANG Z D.Existence of positive bounded entire solutions for quasilinear elliptic equations [J].Applied Mathematics and Computation,2004,156: 743-754. [2]YANG Z D,XU B,WU M Z.Existence of positive boundary blow-up solutions for quasilinear elliptic equations via sub and supersolutions [J].Applied Mathematics and Computation,2007,188: 492-498. [3]LU Q S,YANG Z D,TWIZELL E H.Existence of entire explosive positive solutions of quasi-linear elliptic equations [J].Applied Mathematics and Computation,2004,148: 359-372. [4]LIU C L,YANG Z D.Existence of large solutions for quasilinear elliptic problems with a gradient term [J].Applied Mathematics and Computation,2007,192: 533-545. [5]MIAO Q,YANG Z D.On the existence of multiple positive entire solutions for a quasilinear elliptic systems [J].Applied Mathematics and Computation,2008,198: 12-23. [6]WU M Z,YANG Z D.Existence of boundary blow-up solutions for a class of quasilinear elliptic systems with critical case [J].Applied Mathematics and Computation,2008,198: 574-581. [7]GONCALVES J V,RONCALLI A.Existence,non-existence and asymptotic behavior of blow-up entire solutions of semilinear elliptic equations [J].J Math Anal Appl,2006,321: 524-536. [8]GUO Z M.Some existence and multiplicity results for a class of quasi-linear elliptic eigenvalue problem [J].Nonlinear Anal,1992,18: 957-971. [9]YIN H H,YANG Z D.Some new results on the existence of bounded positive entire solutions for quasilinear elliptic equations [J].Applied Mathematics and Computation,2006,177: 606-613. [10]LIEBERMAN G M.Boundary regularity for solutions of degenerate elliptic equations [J].Nonlinear Anal,1988,12 (11): 1203-1219. [11]KAMIN S,VERON L.Flat core properties associated to the p-Laplace operator [J].Proc Amer Math Soc,1993,118 (4): 1079-1085. [12]LADYZHENSKAYA O A,URAL’TSEVA N N.Linear and quasilinear elliptic equations [M].New York: Academic Press,1968. [13]TOLKSDORF P.On the dirichlet problem for quasilinear equations in domains with conical boundary points[J].Comm Partial Diff Eqns,1983,8 (7): 773-817.1 预备知识和引理



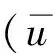




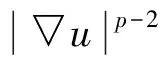






2 主要定理


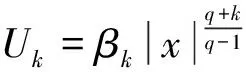

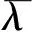



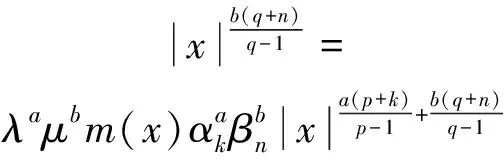





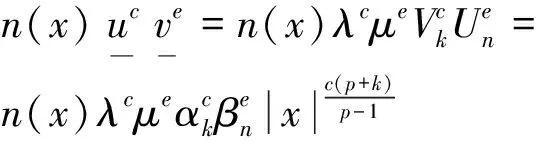





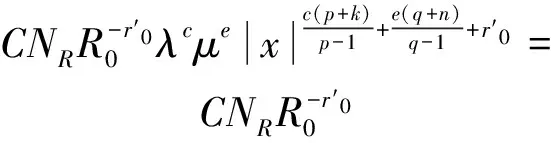


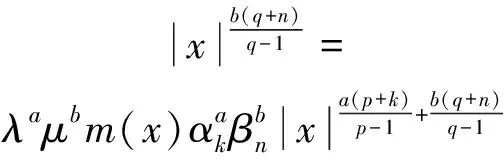














3 结 语

