两类非连通图(P2∨，0,r1,0,…,0,rn)∪St(m)及(P2∨,r2,0,…,0)∪Gr的优美性*

吴跃生,徐保根

(华东交通大学基础科学学院,江西 南昌330013)

图的标号问题是组合数学中一个热门课题。它不仅属于图论领域，也属于设计理论的范畴，主要应用于编码设计、变压器箱设计、雷达脉冲、射电天文学、通讯网络、晶体结构中原子位置的测定和导弹控制码等方面。

1 概念

本文所讨论的图均为无向简单图，V(G)和E(G)分别表示图G的顶点集和边集。

定义1[1]对于一个图G=(V,E)， 如果存在一个单射θ:V(G) →{ 0,1,2,…，|E(G)|}使得对所有边e=(u,v)∈E(G)， 由θ′(e)=|θ(u)-θ(v)|导出的E(G) →{1,2,…,|E(G)|}是一个双射，则称G是优美图,θ是G的一组优美标号，称θ′为G的边上的由θ导出的诱导值。

定义2[2-12]V(G)= (v1,v2,…,vn)的每个顶点vi都粘接了ri条悬挂边(ri≥0是整数，i=1,2,…,n)所得到的图，称为图G的(r1,r2,…,rn)-冠，简记为G(r1,r2,…,rn)。 特别地，当r1=r2=…=rn=r时，称为图G的r-冠。图G的0-冠就是图G。

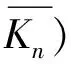
{y1,y2,xi,zj,1≤i≤n,0≤j≤m},

{y1y2,y1xi,y2xi,z0zk,1≤i≤n,0≤k≤m}

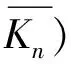
{y1,y2,xi,1≤i≤n}∪V(Gn-1),

{y1y2,y1xi,y2xi,1≤i≤n}∪E(Gn-1)

{y1,y2,xi,x1,s,xn,t,zj,

1≤i≤n,0≤s≤r1,0≤t≤r2,0≤j≤m};

{y1y2,y1xi,y2xi,x1x1,s,xnxn,t,z0zk,

1≤i≤n,0≤s≤r1,0≤t≤r2,1≤k≤m}

{y1,y2,xi,y1,s,y1,t,

1≤i≤n,0≤s≤r1+a,0≤t≤r2}∪V(Gr) ;

{y1y2,y1xi,y2xi,y1y1,s,y2y2,t,

1≤i≤n,0≤s≤r1+a,0≤t≤r2}∪E(Gr),

2 主要结果及其证明

当rj=0时,xj,i=xj,j=1,n;i=1,2,…,rj;

当rj≠0 (j=1,n)时,

θ(x1,i)=2n+m+r1+rn+2-i,i=1,2,…,r1,

θ(y1)=2n+m+rn+1,θ(y2)=2n+m+rn,

θ(xn,i)=2n+m+rn-i,i=1,2,…,rn,

θ(xi)=2(i-1),i=1,2,…,n，

θ(z0)=2n-3;θ(zj)=2n+j-2,j=1,2,…,m

(i)由于

0=θ(x1)<θ(x2)<…<θ(xn-1)<θ(z0)<

θ(xn)<θ(z1)<θ(z2)<…<θ(zm)<

θ(xn,rn)<θ(xn,rn-1)<…<θ(xn,1)<θ(y2)<

θ(y1)<θ(x1,r1)<θ(x1,r1-1)<…<θ(x1,1)=

2n+m+r1+rn+1

(ii)由点标号θ导出的边标号θ′为：

θ′(y1y2)=1,θ′(x1x1,i)=2n+m+r1+rn+2-i,

i=1,2,…,r1，

θ′(y1xi)=2n+m+rn-1-2i,i=1,2,…,n，

θ′(y2xi)=2n+m+rn-2-2i,i=1,2,…,n，

θ′(xnxn,i)=m+rn+2-i,i=1,2,…,rn，

θ′(z0zi)=i+1,i=1,2,…,m

在定理1中，令r1=rn=0,有以下推论。

图1 图(P2∨(0,0,2,0,3)∪St(4)的优美标号

当r1+a=0时,x1,i=x1,i=1,2,…,r1+a;

当r2=0时,x2,i=x2,i=1,2,…,r2;

当r1+a≠0,r2≠0时,

g(y1)=0,g(y2)=n,

g(xi)=3n+r2+1-i,i=1,2,…,n，

g(y2,i)=2n+r2+1-i,i=1,2,…,r2,

g(v)=h(v)+n+1,v∈V(Gr)

(i) 由于

0=g(y1)

g(y2，r2)

g(xn)

g(y1，r1-1)<…

(ii) 由点标号g导出的边标号g′为：

g′(y1y2)=n,g′(xi)=3n+r2+1-i,i=1,2,…,n，

g′(y2y2，i)=2n+r2+1-i,i=1,2,…,r2，

g′(y1xi)=3n+r2+1-i,i=1,2,…,n，

g′(y2xi)=2n+r2+1-i,i=1,2,…,n，

g′(e)=h′(e)，e∈E(Gr)

易见,对于自然数n,r1,r2,a,r,则当n≥2时，

在定理2中，令r1+a=r2=0,有以下推论。

图2 图(P2∨(2,3,0,0,0,0,0,0)∪T6的优美标号

图3 图(P2∨(2,3,0,0,0,0,0,0)∪G5的优美标号

定义7[1]设Cn是长为n的圈，当n>3时，联图(P1∨Cn)称为轮，记Wn。

引理1 所有的轮Wn都是优美图。

图4 图(P2∨(3+4,2,0,…,0)∪W4的优美标号

参考文献：

[1]马杰克.优美图[M].北京:北京大学出版社，1991.

[2]吴跃生，李咏秋.关于圈Cn的(r1,r2,…,rn)-冠(n=7,8)的优美性[J].阜阳师范学院学报：自然科学版， 2010,27(3)：20-23.

[3]吴跃生，李咏秋.关于圈C11的(r1,r2,…,r11)冠的优美性[J].长春师范学院学报，2010,29(6)：4-8.

[4]吴跃生，李咏秋.再探圈Cn的(r1,r2,…,rn)-冠(n=7,8)的优美性[J].阜阳师范学院学报：自然科学版，2010,27(4)：1-4.

[5]吴跃生，李咏秋.关于圈C3的(1,2a,2a+1)-冠的优美性[J].河南教育学院学报，2010,4: 1-2.

[6]吴跃生.关于圈C4h的(r1,r2,…,r4h)-冠的优美性[J].华东交通大学学报,2011,28(1): 77-80.

[7]吴跃生,李咏秋.关于圈C4h+3的(r1,r2,…,r4h)-冠的优美性[J].吉首大学学报：自然科学版，2011,32(6): 1-4.

[8]吴跃生，李咏秋.关于图ω4,4的(r1,r2,…,r7)-冠的优美性[J].宜春学院学报，2010,32(12)：1-3.

[9]吴跃生，李咏秋.关于图ω5，7的(r1,r2,…,r11)-冠的优美性[J].嘉应学院学报，2011,29(5): 5-8.

[10]吴跃生，李咏秋.关于图ω5，6的(r1,r2,…,r10)-冠的优美性[J].北京联合大学学报，2011,25(2): 60-61.

[11]吴跃生.关于图ω4，6的(r1,r2,…,r9)-冠的优美性[J].宜春学院学报，2011,33(8)：1-3.

[12]康芳茂，吴跃生.关于Cn⊙k1的(r0,r1,r2,…,rn)-冠(n=6)的优美性[J].怀化学院学报,2011,30(5): 8-10.

[15]魏丽侠，张昆龙.几类并图的优美标号[J].中山大学学报：自然科学版，2008,47( 3): 10-13.

[16]蔡华，魏丽侠，吕显瑞.非连通图(P1∨Pn)∪Gr和(P1∨Pn)∪ (P3∨Kr)及Wn∪St(m)的优美性[J].吉林大学学报：理学版，2007,45(4): 539-543.

[17]蔡华.几类非连通图的优美性[D].吉林大学硕士学位论文,2007.