长方体有限元的一个校正弱估计

张杰华, 韩明华



长方体有限元的一个校正弱估计

张杰华, 韩明华

(凯里学院 教育科学学院, 贵州 凯里, 556000)

次长方体有限元; 三维投影型插值校正; 弱估计

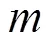
1 三维投影型插值算子

下面介绍本文需要用到的三维投影型插值算子[3, 16].

由Parseval等式(参见文献[4]中第1.4节), 有:

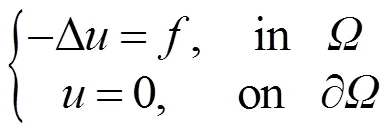
3 弱估计

有了以上准备, 下面讨论有限元解的校正弱估计.

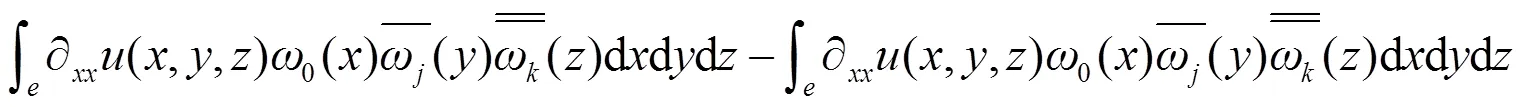
类似的, 可有:

同理可有:

于是利用简单校正格式:

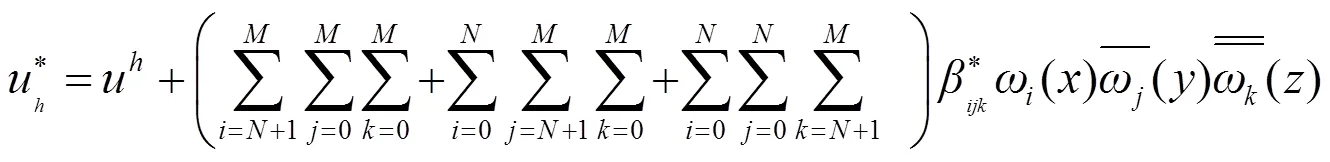
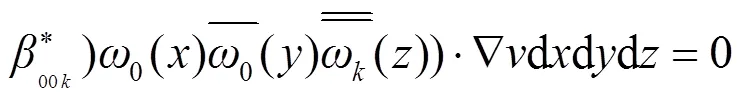
证毕.

4 主要结论

所以, 得出如下主要结论:

证明 首先, 由投影插值定理[3-4, 11], 有:

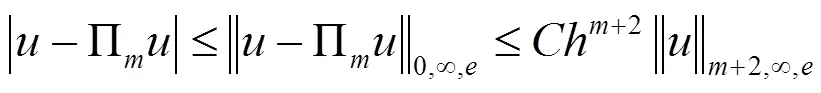
[1] 林群, 严宁宁. 高效有限元构造与分析[M]. 保定: 河北大学出版社, 1996.

[2] 朱起定, 林群. 有限元超收敛理论[M]. 长沙: 湖南科学技术出版社, 1989.

[3] 朱起定. 有限元高精度后处理理论[M]. 北京: 科学出版社, 2008.

[4] 林群, 朱起定. 有限元预处理和后处理理论[M]. 上海: 上海科学技术出版社, 1994.

[5] Chen Chuanmiao. Orthogonality Correction Technique In Superconvergence Analysis[J]. International Journal of Numerical Analysis And Modeling, 2005, 2(1): 31-42.

[6] Zhu Qiding, Zhao Qinghua. Spr Technique And Finite Element Correction[J]. Numer Math, 2003, 96: 185-196.

[7] Lin Qun, Zhou Aihui. Defect Correction For Finiteele Gradient[J]. Systems Sciences And Mathematical Sciences, 1992, 5(3): 287-288.

[8] Zhang Yunzhang, Hou Yanren, Mu baoying. defect Correction Method For Time-Dependent Viscoelastic Fluid Flow[J]. International Journal of Computer Mathematics, 2011, 88(7): 1546-1563.

[9] Si Zhiyong, He Yinnian, Wang Kun. A Defect-Correction Method For Unsteady Conduction Convection Problems I: Spatial Discretization[J]. Science China: Mathematics, 2011, 54(1): 185-204.

[10] 范馨月, 杨一都. 非自共扼椭圆特征值问题有限元插值校正[J]. 计算数学, 2011, 33(1): 15-25.

[11] Liu Jinghong, Jia Bo, Zhu Qiding. An Estimate For The Three-Dimensional Discrete GreenS Function And Applications[J]. J Math Anal Appl, 2010, 370: 350-363.

[12] Liu Jinghong, Sun Haina1, Zhu Qiding. Superconvergence Of Tricubic Block Finite Elements[J]. Science in China Series A: Mathematics, 2009, 52(5): 959-972.

[13] Liu Jinghong, Huo Xiaocheng, Zhu Qiding. Pointwise Supercloseness of Quadratic Serendipity Block Finite Elements For A Variable Coefficient Elliptic Equation[J]. Numerical Methods For Partial Differential Equations, 2011, 27(5): 1253-1261.

[14] Liu Jinghong, Zhu Qiding. Pointwise Supercloseness of Pentahedral Finite Elements[J]. Numerical Methods For Partial Differential Equations, 2010, 26(6): 1572-1580.

[15] Liu Jinghong, Zhu Qiding. Pointwise Supercloseness of Tensor-Product Block Finite Elements[J]. Numerical Methods For Partial Differential Equations, 2009, 25(4): 999-1008.

[16] Liu Jinghong, Sun Haina, zhu Qiding. superconvergence of Tricubic Block Finite Elements[J]. Science in China Series A: Mathematics, 2009, 52(5): 959-972.

A weak correction estimate of block finite element

ZHANG Jie-hua, HAN Ming-hua

(Institute of Educational Science, Kaili University, Kaili 556000, China)

block finite element of degree; three dimensions projection interpolation correction; weak estimate

O 242.21

1672-6146(2012)01-0014-05

10.3969/j.issn.1672-6146.2012.01.005

2011-12-09

凯里学院院级规划课题资助项目(z1019)

张杰华(1981-), 男, 讲师, 硕士, 主要从事有限元超收敛理论研究. E-mail: xtsowxf2006@163.com

(责任编校:刘晓霞)