考虑干涉情况的多台龙门吊作业路径优化
林艳艳,乐美龙
(上海海事大学科学研究院,上海 201306)
0 引言
随着世界经济的快速发展,集装箱港口的竞争越来越激烈,如何在众多竞争者中脱颖而出是现代集装箱港口面临的首要问题.现在的关键是通过提高集装箱港口的装卸效率实现降低成本、提高竞争力的目标.在集装箱港口的后方堆场中,由于龙门吊尺寸过大且移动速度较为缓慢,其在不同箱区之间作业时,过道转弯作业会占据大量道路空间,有可能因此导致堆场内交通堵塞并耽搁集卡、甚至是其他船舶的作业.显然,场桥作业调度的优劣不但会影响自身的作业效率,还会对码头整体作业水平产生影响.因此,如何提高龙门吊的工作效率,成为当前众多研究者探讨的热点问题.
1 文献综述
到目前为止,针对龙门吊的作业优化主要可以分为龙门吊调度优化[1]、龙门吊配置优化[2]以及龙门吊路径优化研究.龙门吊路径优化研究的主要贡献如下:
KIM等[3]研究龙门吊处理出口集装箱的路径优化问题.决策变量是龙门吊在堆场贝位上提取的集装箱数量和龙门吊到达贝位的序列,并构建混合整数规划模型.目标函数为最小化龙门吊装卸集装箱的总时间,包括在贝位的处理时间和贝位间的运行时间.文中只考虑出港装载操作.同时,作者设计出一个路径优化算法.
KIM等[4]在1997年研究的基础上,将设计模型分解为几个子问题,其中每个子问题都可以由动态规划算法求解.算法能够较好地求得最优解,但是只适合于小型或中型船舶,大型船舶的问题则需要设计一个启发式算法进行求解得到近似解.
NARASIMHAN等[5]首次证明龙门吊路径优化问题是一个NP完全问题,然后运用分支定界法计算该问题.在此基础上,设计一个最坏案例的实现率(1.5)的列数启发式算法.作者提出的模型以实现龙门吊完成给定装载计划所花费的时间最小为目的;但文中给出的模型过于简单,且没有考虑约束条件;主要设计4种算法,并通过算例进行比较与分析;最后得出,分支定界法适合小规模问题的求解,而启发式算法则适合于较大规模的问题,且随着港口不同,算法性能也会随之改变.
KIM等[6]再次研究集装箱港口后方堆场装卸设备的路径优化问题.在之前研究的基础上,运用遗传算法(Genetic Algorithm,GA)和约束搜索方法求解该问题.在算例分析中将这两种算法与精确算法进行比较;但文中对设计的两种算法的描述不够详细;在算例分析中分别进行中小型问题的3种算法的比较,能够较直观地表现出3种算法的计算性能.
韩晓龙[7]研究一台龙门吊的路径优化问题,建立以龙门吊总工作时间最短为目标的混合整数规划模型.首先按照龙门吊就近服务的原则给出龙门吊的路径及其启动次数和工作时间;再对模型运用LINGO 8.0进行计算,得出优化的龙门吊路径;最后将两者进行比较,得出设计模型的有效性.
LEE等[8]讨论双龙门吊系统的调度问题,主要描述在两个不同箱区的两台龙门吊的集装箱装载操作.建立数学模型,并运用模拟退火(Simulated Annealing,SA)算法进行求解.模型中假设对两台龙门吊同时调度,装载计划和箱区计划已知,两台龙门吊同时服务于一台桥吊.但是模型中没有考虑箱区上集装箱的时间序列,也即未考虑集装箱的需求时间,只考虑集装箱的数量.在装载过程中,龙门吊不会在两个箱区间移动,那么就可以将问题分为两个单一龙门吊的问题.作者又提出一个最低界评估的算法,用于与SA算法进行比较,虽然得出的结果是SA的方案比最低界评估的方案差10.3%,但是如果不需要精确解的话,SA算法的结果还是比较满意的,且可以知道SA算法与集装箱装载的数量相互独立,可以处理大规模的问题.
CAO等[9]主要研究用一个龙门吊调度系统服务装船作业的问题,目标是最小化龙门吊总完成时间.设计一个贪婪算法、SA及龙门吊调度启发式算法求解该问题.该系统由一大一小两台龙门吊构成,在模型中除了有与普通两台龙门吊调度相同的约束外,还设计了避免干涉约束.但是,在技术上没有考虑大的龙门吊和小的龙门吊的额定工作能力的不同限制.设计的贪婪算法,只有规则,没有具体的算法步骤.GA也只是考虑两台龙门吊的情景,没有考虑这个模型的特殊性,即没有考虑一大一小龙门吊的优越性.在算例分析中,较好的一点是对多个算法进行比较.
李丽丽[10]在研究集装箱堆场布局的基础上,将堆场中的各个功能区抽象为一个节点建立各个功能区之间的连通图,提出利用最短路法和动态法的综合路径优化求解法,建立龙门吊路径优化模型,并给出基于GA的求解过程,最后运用Flexsim进行仿真求解验证上述问题的最优结果.
从上面的文献综述中可以了解到,目前对龙门吊的路径优化研究较少,且大多只局限于对一台龙门吊的路径优化.即使是研究两台龙门吊的路径优化,也只是两台龙门吊在两个不同的箱区,而没有考虑到多台龙门吊在同一个箱区协同工作的情况.因此,研究者在研究龙门吊路径优化时,很少考虑龙门吊之间的干涉问题,即使有所考虑,也很少会将其纳入计算中.目前,关于龙门吊之间干涉问题的研究主要有以下两种假设约束:一是假设龙门吊之间发生干涉时,则一台龙门吊停止等待另一台龙门吊工作完成,见文献[9]和[11];一是假设避免龙门吊之间的干涉,并设定龙门吊之间的安全距离,见文献[12]~[14].本文在模型中考虑的干涉约束沿用第一种假设,而在计算中则假设龙门吊发生干涉时等待2 min,然后两台龙门吊的工作互换.
2 多台龙门吊路径优化研究
龙门吊路径优化和VRP问题都是路径优化研究,但是两者最大的不同之处是:VRP只需要确定最优路径,而龙门吊路径优化研究是在确定龙门吊最优路径的同时,还要确定龙门吊在路径中每个贝位上提取的集装箱数量.
本文主要是以KIM等[6]提出的单台龙门吊的路径优化研究为基础,提出多台龙门吊的路径优化研究.龙门吊路径优化研究的重要前提是已知集装箱堆场贝位上的集装箱分布情况,即已知堆场分布图,见图1.出于安全因素考虑,每个贝位的集装箱堆存不能超过7列、4层;且在第4层的左右两端必须空出,以避免由于风、雨、雪等因素引起集装箱倾倒的危险.这样,每个贝位上最多堆存的集装箱数为26个,且只能堆存同一种类型的集装箱.

图1 堆场分布
本文集装箱组的设计沿用KIM等[6]制定的集装箱组分类方法,即按照集装箱的目的港及集装箱尺寸进行分类,另外还新加入集装箱重量这一参数,即在设计时协同考虑这三要素,这主要是满足出口箱装船时船舶对集装箱重量的要求.图1中,不同颜色代表不同的集装箱组,如贝位1和贝位7堆存不同数量的同种类型的集装箱,其集装箱组的目的港为BANGKOK,20英尺箱,且重量相同.
掌握堆场分布图后,根据研究需要细化出每个箱区的集装箱组分布情况,得到堆场计划表,见表1(表中给出贝位数P=15情况下的堆场计划表).从表中可以了解到在贝位1中有A组集装箱9 TEU,在贝位2中有B组集装箱19 TEU,依此类推.

表1 堆场计划表说明(P=15)
多台龙门吊路径优化研究的另一个重要前提是了解集装箱的装船计划,即装载计划表,见表2(表中给出P=15情况下的装载计划表),其中子任务表示龙门吊需要完成的装载任务的子任务.

表2 装载计划表说明(P=15)
已知这些数据后,通过建立多台龙门吊的路径优化模型,并运用C#_2008编程,再用Gurobi_4.5求解,计算得到每台龙门吊的最优路径及在每个贝位上提取的集装箱数量.
3 模型
3.1 问题描述
研究针对的是在集装箱港口中多台龙门吊同时服务一条船装载出口箱的情景.由于龙门吊本身形状的特殊性,堆场上每个箱区中最多只能有两台龙门吊.根据所研究的龙门吊服务的具体情形,可知两台龙门吊同时完成一个任务.根据装载计划获知一个任务可以划分为几个子任务.如表2所示,一个任务划分为8个子任务,在子任务中要提取A集装箱组中的18 TEU,在子任务2中要提取B集装箱组中的15 TEU,依次类推.
为了切合实际,模型遵循以下假设条件:
(1)只考虑出口集装箱,因此集装箱的贝位图一般已知,即堆场上的集装箱分布情况已知;
(2)研究龙门吊处理出口集装箱的装载优化,因此其研究前提即装载计划已知;
(3)由于龙门吊的尺寸较为庞大,一个箱区最多只能有两台龙门吊同时工作;
(4)只考虑一个运行方向上的集装箱箱区,即龙门吊行走无须转弯,不必考虑龙门吊转过场的时间(一般出口集装箱会集中堆放,这既符合实际情况,又降低研究难度);
(5)进行分组装载优化,因此只考虑一种标准箱型(20英尺箱)有利于优化研究;
(6)只考虑出口集装箱组,且每个贝位上只有一种集装箱组,此为研究前提.
3.2 模型描述
设计多台龙门吊的综合优化混合整数规划模型,模型中考虑龙门吊之间的干涉问题.首先解释说明模型中相关字母的涵义.
m为组成一台龙门吊的一个任务的子任务数量;n为龙门吊数量;P为堆场贝位数量;Q为集装箱组数量;K={1 ,2,…,n}为龙门吊的索引集;B={1,2,3,…,p}为堆场贝位的索引集;G={1,2,3,…,q}为集装箱组的索引集(即对堆场贝位和集装箱组都进行编号);S(h)为与集装箱组h相对应的子任务编号集;B(h)为堆场贝位集,其中该贝位上的集装箱组为h;ch,j为堆存在贝位j上的集装箱组h的初始数量;rt为子任务t中提取的集装箱数量;gt为在子任务t中必须提取的集装箱组数;B(gt)为在子任务t中必须提取的集装箱组所在的堆场贝位集.
可以将龙门吊路径优化问题描述为一个网络图问题.一个网络图由点集V和弧集A构成(见图2).

图2 龙门吊作业路径网络
在本模型中,假设一个点由t(i)表示,其中t表示子任务数,i表示堆场贝位数,则该问题就变成在网络中从初始贝位S点到终点贝位T点找到每台龙门吊的一条路径,并决定它们在每个点上提取的集装箱数.A(V)为弧集,A(V)={(i,j)|i,j∈V},且点集V是给定的;S={S1,S2,…,Sn}为龙门吊的出发点集,且 S⊂B;T={T1,T2,…,Tn}为龙门吊的结束点集,且 T⊂B;t=0,1,…,m,m+1,其中 t=0 表示龙门吊在初始位置,而t=m+1则表示龙门吊在终点位置;Ts为龙门吊在每个堆场贝位的调整时间;Td为每个堆场贝位的长度;Tv为龙门吊的运行速度;Th为龙门吊装卸一个集装箱的时间.
决策变量:
经过我们与盲人的深入交流,结合上网分析查阅,我们发现盲人在病患方面有较多顾虑,并且医疗器械方面的温度计没有针对盲人研发专门的盲人用便捷温度计。于是我们小组希望针对盲人设计其专门使用的温度计,以改善盲人的生活质量。
综上,考虑干涉的多台龙门吊路径优化模型可表述如下:

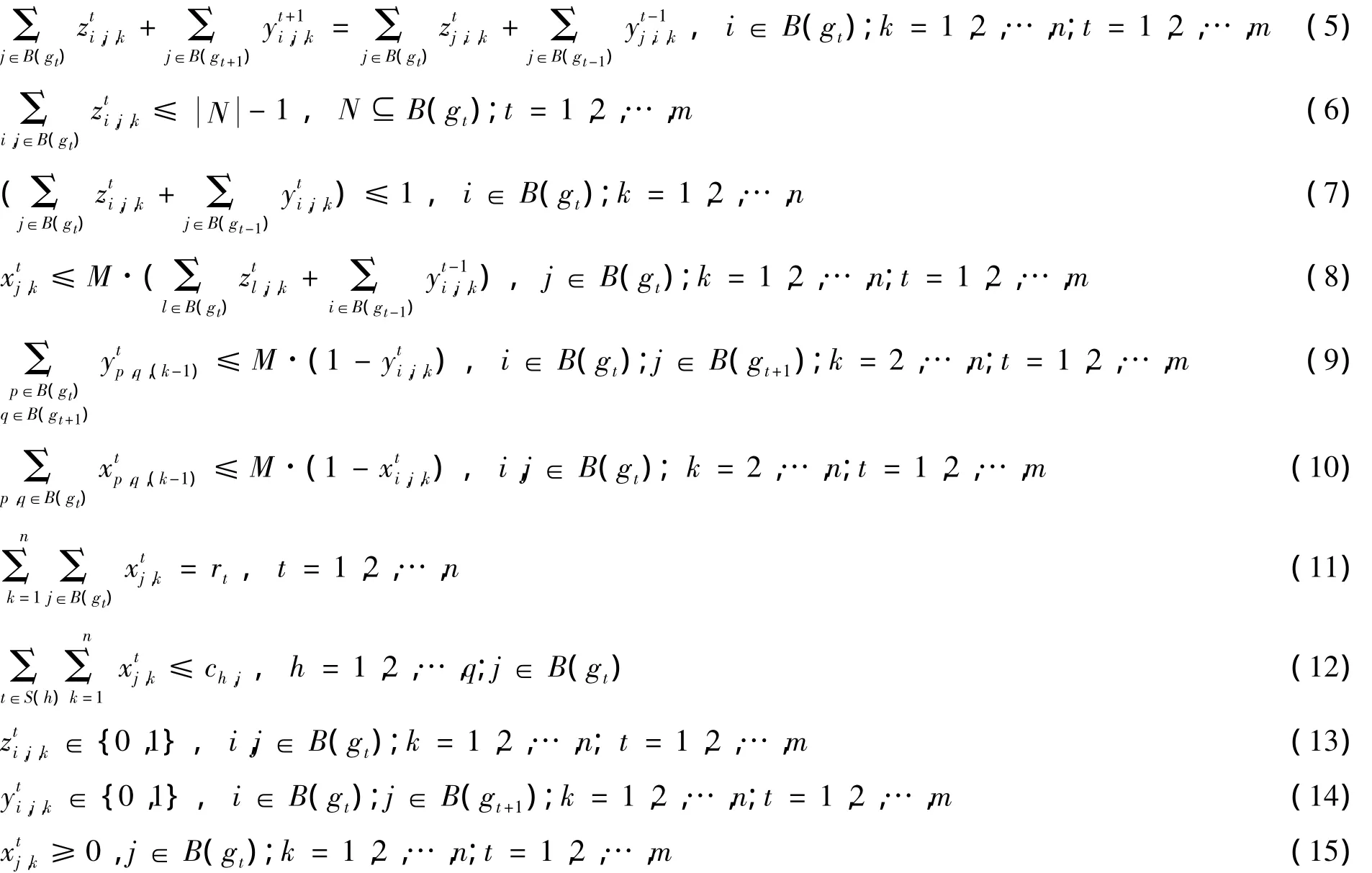
其中:式(1)为目标函数,表示最小化总时间,包括龙门吊的运行时间、准备时间及处理集装箱的时间;式(2)为约束条件,表示每个箱区的龙门吊数量不能超过2台;式(3)~(5)共同控制龙门吊路径网络的流量,其中式(3)和(4)表示每个任务的出发点的出度和结束点的入度均为1,式(5)表示中间节点的出度等于入度;式(6)和(7)共同保证龙门吊的运行路径不会出现内循环;式(8)表示龙门吊只有到达贝位才可以开始作业;式(9)和(10)保证避免龙门吊之间的干涉;式(11)表示龙门吊要满足每个任务要求提取的集装箱数量;式(12)表示龙门吊提取的集装箱数量不能超过贝位上原有的集装箱数量;式(13)和(14)为(0,1)决策变量的约束;式(15)表示该决策变量为非负数.
4 算例设计及分析
首先,对第3节中构建的模型,结合某港口的实际数据对其进行算例设计.本算例主要是针对一个箱区上的装船任务,即在龙门吊的数量n=2的情况下,分别进行3组试验(P,Q,m)=(15,3,8),(25,4,10),(35,4,11).其中,由该港口的实际情况得到每个贝位的长为Td=6.096 m,龙门吊的运行速度为Tv=30 m/min,龙门吊处理一个集装箱的时间Th=2 min,而龙门吊的调整时间Ts=1 min.关于P=15的案例的具体实验数据见表1和2,而P=25和35的案例的具体数据见表3和4(为了简化,将装载计划表与堆场计划表合并组成集装箱装载计划).

表3 集装箱装载计划(P=25)
运用C#_2008进行编程,并调用Gurobi_4.5进行计算.对上述设计的每个算例均进行10次重复计算,得到较为稳定的计算结果,且计算时间均在理想范围内.
图3表示3种案例的龙门吊行走路径,横轴表示子任务,纵轴表示贝位.图中,两条路径交点处表示两台龙门吊在一个子任务内均到达过的贝位,由于计算中加入避免干涉的条件,可以由图中看出,每个子任务中两台龙门吊到达同一贝位的时间是错开 的,因此没有发生干涉.
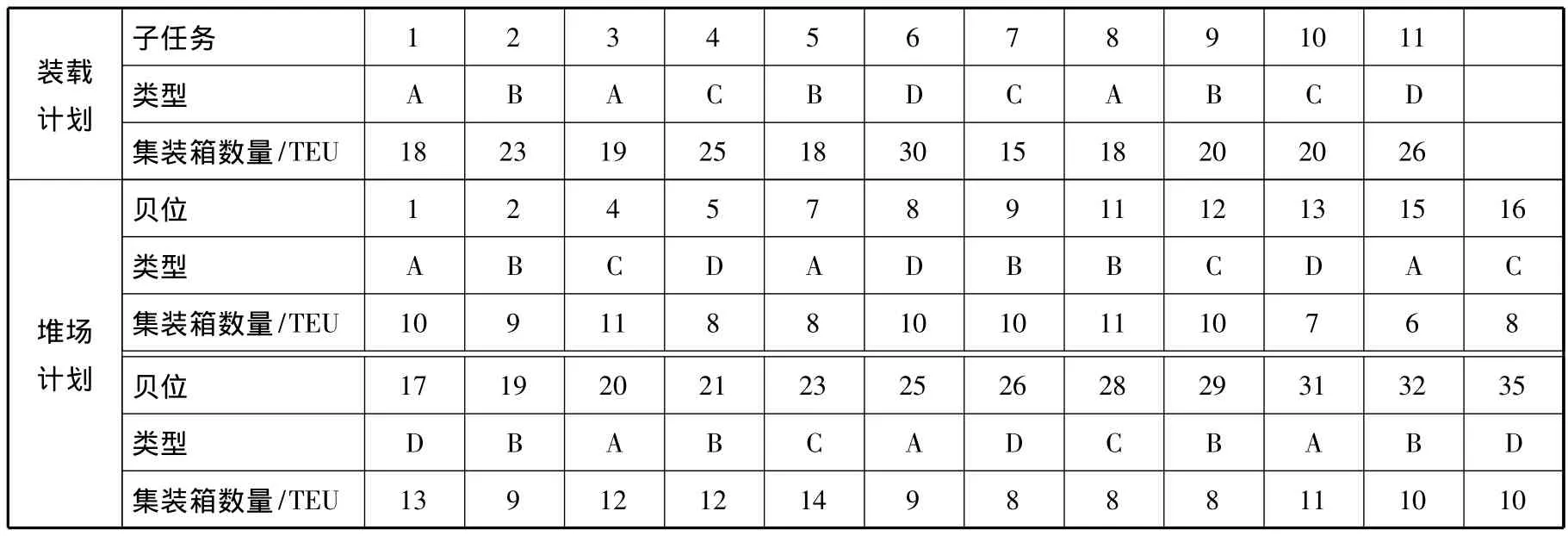
表4 集装箱装载计划(P=35)

图3 龙门吊最优路径

表5 龙门吊在不同贝位和子任务中提取的集装箱数量(P=15)TEU

表6 龙门吊在不同贝位和子任务中提取的集装箱数量(P=25)TEU
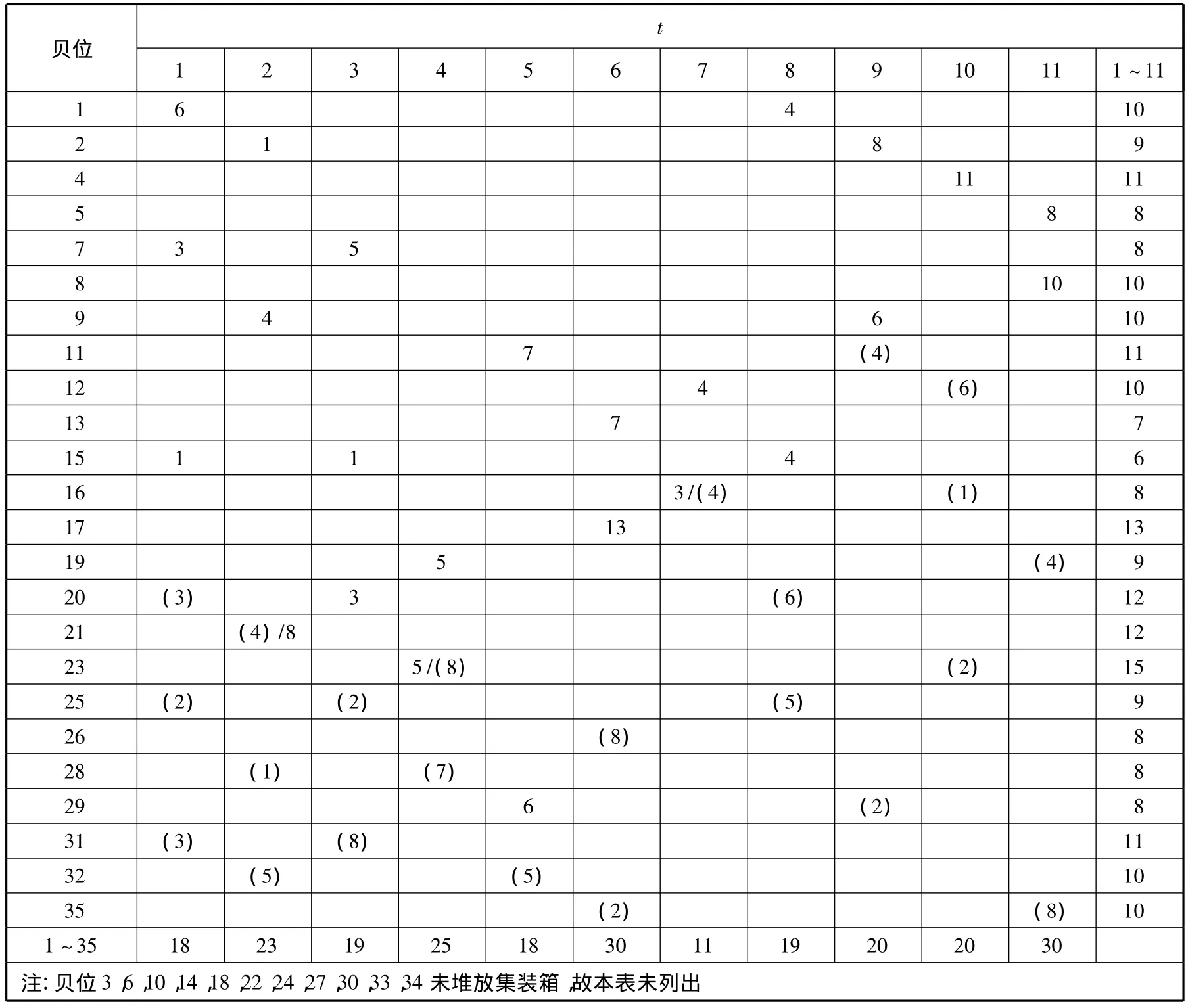
表7 龙门吊在不同贝位和子任务中提取的集装箱数量(P=35)TEU
从上述各表中可以清楚地看出每个案例中龙门吊的启动频率(即访问贝位的次数)和龙门吊在每个子任务及每个贝位上提取的集装箱数.为了进一步研究龙门吊的路径优化问题,同时计算一台龙门吊处理上述任务的总时间以及启动频率,然后将一台龙门吊与两台龙门吊的优化结果进行比较,结果见表8.

表8 单台龙门吊和多台龙门吊工作效率的比较
从表8中可以发现,两台龙门吊处理任务的时间明显少于一台龙门吊,几乎能够节省一半时间.虽然一台龙门吊的启动频率少于两台龙门吊的总启动频率,但平均下来,一台龙门吊的启动频率大于两台龙门吊的单台启动频率.因此,在处理同一任务时,两台龙门吊的工作效率高于一台龙门吊的工作效率,从而验证模型是可行有效的.
5 总结与展望
以KIM等[6]提出的单台龙门吊路径优化问题的模型为基础设计多台龙门吊的路径优化研究.模型中考虑多台龙门吊的干涉问题,并对集装箱组的分类方法进行更新.在未来研究中,需要对更大规模的实例作进一步设计分析,更需要设计新的启发式算法进行计算,以加快计算速度.
[1]何军良,宓为建,严伟.基于爬山算法的集装箱堆场场桥调度[J].上海海事大学学报,2007,28(4):11-15.
[2]金鑫,丁以中.新工艺下集装箱码头装卸资源分配模拟[J].上海海事大学学报,2010,31(1):28-32.
[3]KIM Ki Young,KIM Kap Hwan.A routeing algorithm for a single transfer crane to load export containers onto a container ship[J].Computers &Ind Eng,1997,33(3/4):673-676.
[4]KIM Ki Young,KIM Kap Hwan.An optimal routeing algorithm for a transfer crane in port container terminals[J].Transportation Sci,1999,33(1):17-33.
[5]NARASIMHAN A,PALEKAR U S.Analysis and algorithms for the transtainer routeing problem in container port operations[J].Transportation Sci,2002,36(1):63-78.
[6]KIM Ki Young,KIM Kap Hwan.Heuristic algorithm for routeing yard-side equipment for minimizing loading times in container terminals[J].Naval Res Logistics,2003,(50):498-514.
[7]韩晓龙.集装箱港口龙门吊的最优路径问题[J].上海海事大学学报,2005,26(2):39-41.
[8]LEE Der-Horng,CAO Zhi,MENG Qiang.Scheduling of two-transtainer systems for loading outbound containers in port container terminals with simulated annealing algorithm[J].Sci Direct,Int J Production Econ,2007,107(1):115-124.
[9]CAO Zhi,LEE Der-Horng,MENG Qiang.Deployment strategies of double-rail-mounted gantry crane systems for loading outbound containers in container terminals[J].Int J Production Econ,2008,115(1):221-228.
[10]李丽丽.集装箱堆场布局与场桥调度优化研究[D].大连:大连海事大学,2011.
[11]NG W C.Crane scheduling in container yards with inter-crane interference[J].Eur J Operational Res,2005,164:64-78.
[12]JAVANSHIR H,GANJI S R S.Yard crane scheduling in port container terminals using genetic algorithm[J].J Ind Eng Int,2010,6(11):39-50.
[13]MAK Kai Ling,SUN Di.A scheduling method for cranes in a container yard with inter-crane interference[J].Electronic Eng & Computing Technol,2010,60:715-725.
[14]HU Zhihua.Improved discrete time model for container yard crane scheduling[C]//2010 Third Int Joint Conf Computational Sci& Optimization-Volume 02 IEEE Computer Society Washington,DC,USA.2010:34-37.

