轴辐式快递网络的枢纽选址和分配优化

李莉，丁以中

(上海海事大学 科学研究院，上海 201306)

0 引言

顺丰和申通等快递企业以小件货物运输为主要业务，采用轴辐式网络［1］作为运输组织方式.轴辐式快递网络是指运送线路的安排以某几个城市为枢纽，枢纽城市之间开行直达运送车辆，而其他城市之间没有直达运送线路，只与其相近的枢纽城市相连，通过枢纽进行中转衔接的快递网络.图1为10个节点形成的轴辐式快递网络，节点3，5和10为枢纽点.轴辐式快递网络中，节点之间的运输必须通过枢纽点中转完成.如节点1与节点8之间的快递需要经过两个枢纽中转:首先由节点1收集该服务区域内的客户快件，汇集后发往枢纽点3;然后由枢纽点3直接发往枢纽点10;最后由枢纽点10发往节点8，完成节点1至节点8的快件运输过程.节点1与节点2之间的快递经过一个枢纽中转，分析过程同上，行走路线为1－3－2.而枢纽之间的运输无须中转，枢纽3，5，10之间是直达运输.

图1 10节点轴辐式快递网络

轴辐式快递网络规划包括枢纽选址和分配方案确定两个方面.现有文献中关于枢纽选址研究较多的是P枢纽中位问题［2］，该问题研究的是已知需求节点之间的运输需求和所需建立的枢纽个数，求出枢纽位置、非枢纽点对枢纽的分配方式，使得总的运输成本(时间，距离等)最小.而P枢纽中位问题忽略轴辐式快递网络的缺陷:节点收集的货物必须通过一个或两个枢纽点集中、分拣，由于中转而行走的路径使快件到达时间延长，如由节点1发出的货物沿着路径 1－3－10－8 到达服务点 8，所需时间大于节点1直接运到节点8所需时间，可能无法保证“最差服务水平”，即节点之间所能允许的最长服务时间.因此，希望节点之间的运输能够在一定时间约束下完成，以保证总的成本最低;满足中转货物的时效要求，节点之间最长的运输时间要最小化，即多目标轴辐式快递网络的枢纽选址和分配优化问题.

现有文献中关于轴辐式网络设计优化研究，所建立的模型均为单目标优化模型，以总的运输成本最低为目标.如文献［2］考虑星状轴辐网络P枢纽中位问题，以总的服务时间最短为目标;文献［3］研究货物运输系统的枢纽选址问题，综合考虑运输时间、装卸时间、分拣时间以及中转时间，建立最小化最迟到达火车时间的非线性混合整数规划模型，模型仅适用于小范围地区的货物运输;也有以服务范围的覆盖率最大为目标，如文献［4］以土耳其货物运输系统为研究对象，建立最少枢纽个数的最大化覆盖模型.

然而，快递公司在进行轴辐式快递网络设计优化过程中，降低运营成本和满足中转货物时效要求同等重要.因此，在进行网络设计时，综合考虑成本、服务水平等因素，建立多目标优化模型更符合实际.现有文献中，多目标轴辐式网络设计问题的文献较少.其中:COSTA等［5］首次建立多目标枢纽选址模型，通过添加另一个目标函数——枢纽处理货物的时间最小化，来表示枢纽的处理能力限制这一约束.作者主要从理论角度建立多目标枢纽选址模型，没有考虑现实因素.国内学者张健［6］研究公路快运轴辐网络问题，首次综合考虑成本、运输安全性和调度难度，建立多目标优化模型，用主要目标法把安全性目标和方便性目标转化为问题约束;采用拉格朗日松弛技术将安全约束和方便性约束转化为惩罚项纳入目标函数，结合层析遗传算法和分支定界方法求解模型，提出安全参数和方便性参数的设置原则.他们针对网络的运载优化建立多目标优化模型，即前提是货运站与中转站之间的指派关系已经确定，建立的是单分配模型，目标是进行车型选择和求出车辆行走路径;求解方法将路线确定和车辆类型选择分别作为单一问题进行优化;将子网和主干网络分别进行优化，缺乏整体最优理念.

同时，在算法方面，O’KELLY［7］首先研究 P 枢纽中位问题，验证为组合优化问题.轴辐式快递网络配置模型和P枢纽中位问题的相同点是都包括枢纽选址和分配方案确定，亦有NP难特性.由于多目标轴辐式网络设计问题研究和相关算法都较少，而关于多目标优化问题的相关算法较多，盛丽俊等［8］和白治江等［9］利用遗传算法求解多目标模型，SINGH 等［10］用模拟退火(Simulated Annealing，SA)算法进行求解.由于SA算法的通用性较强，对问题信息依赖较少，尝试用该算法求解文中问题.

1 模型

1.1 模型假设

轴辐式网络中，如果将网络中所有非枢纽点仅分配给一个枢纽点，称之为单分配轴辐式网络;如果可以将网络中的非枢纽点分配给多个枢纽，称之为多分配轴辐式网络，如将图1中的非枢纽点4分配给枢纽点3和枢纽点5，是一个多分配轴辐式网络图.由于快递网络是多层级网络，文中研究的是快递网络核心部分所对应的多分配轴辐式快递网络设计问题，仅考虑快递网络的第1层和第2层.

建立的多目标优化模型基于以下假设:(1)两两节点之间的发货量小于车辆的车载容量;(2)枢纽之间的运输有运输折扣;(3)非枢纽点之间不能直接连接，必须通过一个或者两个枢纽点进行连接;(4)枢纽是全连接的.

模型假设的合理性验证:(1)如果出现节点之间货运量大于车载容量的情况，则可以先进行整车的直达运输，剩余的货运量归入问题中;(2)称枢纽之间的运输为干线运输，枢纽与非枢纽之间的运输为支线运输.干线上车辆的满载率等因素形成规模效应，因此干线上的单位运输成本降低，用运输折扣表示;(3)假定节点间的距离满足三角不等式，根据轴辐式网络“中转”特征，节点之间的运输必须通过“至少一个枢纽，至多两个枢纽”完成.由以上分析得出模型假设合理.

1.2 问题描述和符号说明

给定的节点集合S={1，2，…，N}，进行轴辐式快递网络的设计优化:选择枢纽的个数和位置，非枢纽对枢纽的分配方案形成图1式的轴辐式快递网络.给定节点之间的快递量、单位运输成本、节点间的运输时间、服务时间限制等，具体如下:

qij为节点(i，j)之间的快递量;Cij为路段(i，j)的单位运输费用;fij为路段(i，j)的固定费用;gi为经过节点i所需的单位中转费用;sk·ln nk为节点k处的分拣费用;tij为路段(i，j)的运输时间;Tij表示节点(i，j)之间的时间限制;Lij表示节点(i，j)之间的路径;(u，v)∈Lij表示节点对(u，v)在路径上形成路段(u，v).

1.3 模型建立

建模的目的是确定枢纽点个数、位置和运作计划，以达到网络总成本最低.考虑到轴辐网络的规模经济性［11］，运输费用为固定路段成本与变动运输成本之和:随着流量的增加，单位流量分摊的固定成本降低;相应地，单位成本降低，是符合实际的一种费用表达方式.

本节建立的非线性整数规划模型中，枢纽个数作为决策变量之一，用0－1变量表示节点是否为枢纽点，决策变量设计如下:

设枢纽之间的运输折扣率为α，表示如果节点(i，j)为枢纽点，则两者之间的单位运输费用为αCij.建立如下多目标轴辐式公路快递网络的配置优化模型:

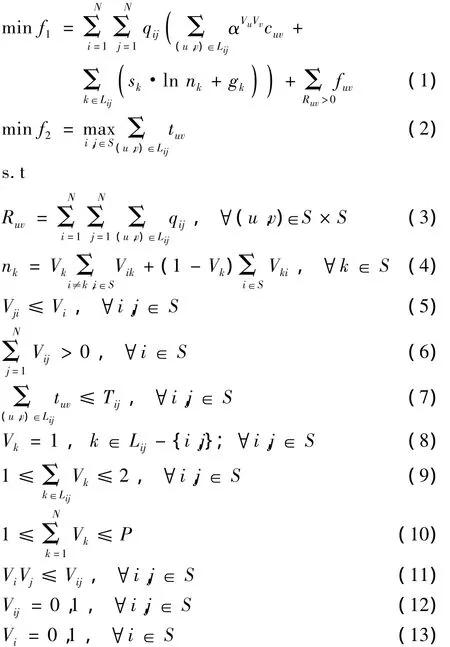
式(1)为完成所有快递量的总费用，节点(i，j)之间的行走路径为Lij，这条路径上的单位成本包括单位运输成本、单位分拣成本，具体表示为

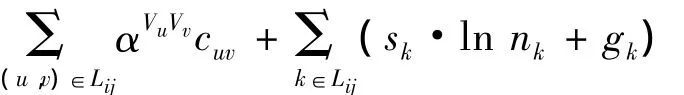
2 算法设计

SA算法进行模型(1)～(13)的求解.该算法是基于蒙特卡洛迭代求解策略的一种随机寻优算法，基于物理中固体物质的退火过程与一般组合优化问题之间的相似性.在某一温度下，伴随温度参数的不断下降，SA算法结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即局部最优解能概率性地跳出并最终趋于全局最优.［12］利用SA算法通用性强、对问题的信息依赖较少、能够保证解的多样性等特征，针对文中模型设计SA算法，通过枢纽搜索策略和非枢纽搜索策略的设置，产生更接近帕累托最优前沿面的近似集，提供一种求解多目标轴辐式快递网络的启发式算法.

2.1 SA算法要素

图2为多目标优化SA算法流程.单一温度下内部循环中的Floyd算法和数据标准化具体设计如下.

2.1.1 Floyd算法设计

给定轴辐式快递网络的设计方案Vij，即确定枢纽位置和个数、非枢纽的分配方案，利用Floyd算法求解各节点对(i，j)之间的最短路径Lij:用节点之间快递运输所需的总费用表示两者之间的距离.求解最短距离过程中，各节点之间的运输总时间必须限制在时间约束Tij内;如果节点之间的行走路径不满足时间约束，则选择行走时间最短的路径.

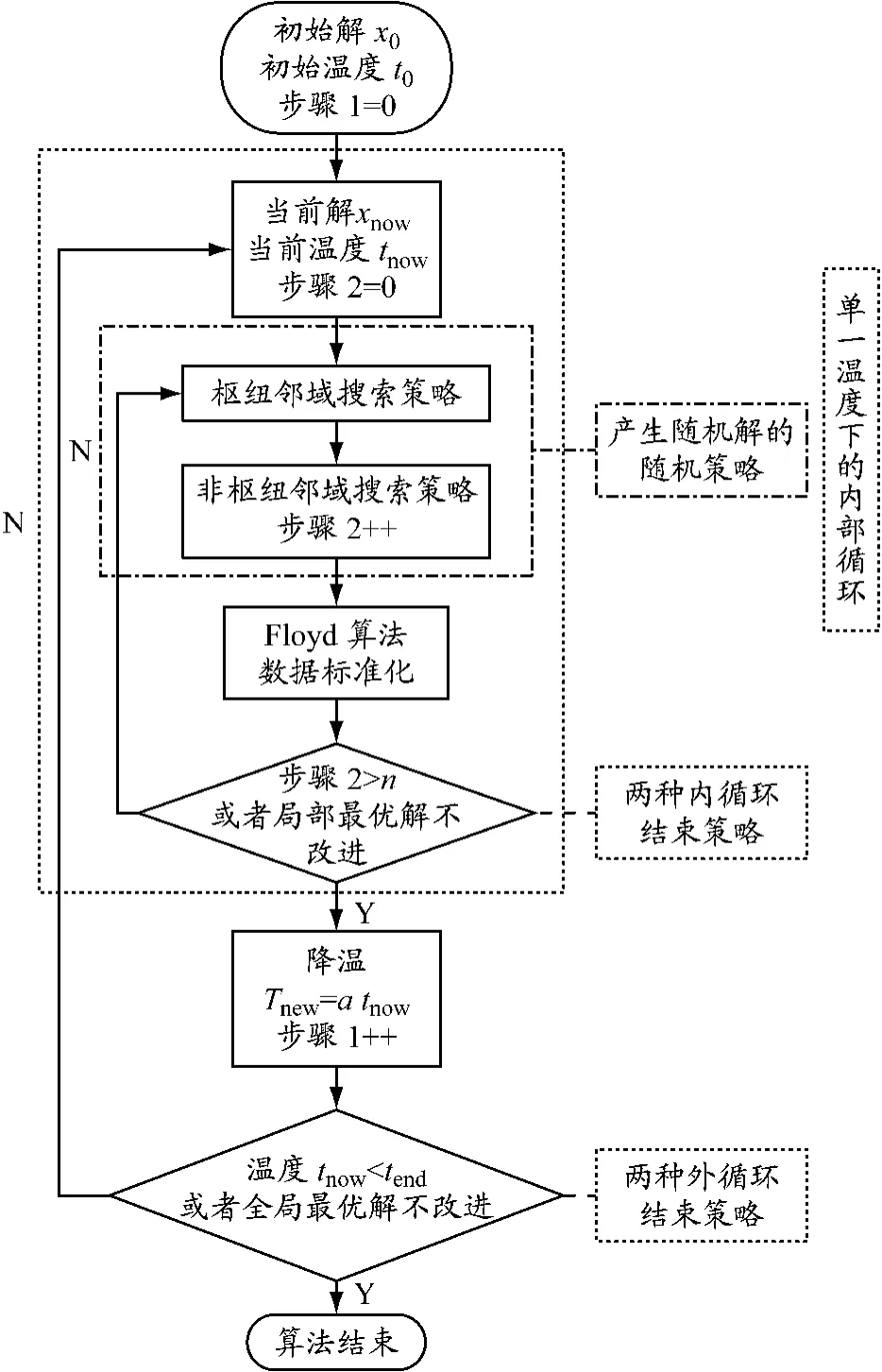
图2 多目标优化SA算法流程

2.1.2 数据标准化

采用综合目标评价的方法进行多目标轴辐式快递网络设计优化，由于成本和时间的量纲不同，对数据进行标准化并建立合理的加权综合目标.下面分别对成本值(Vc)和时间(t)进行标准化:

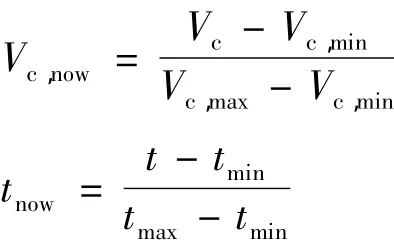
式中:Vc，max，Vc，min为成本的极大值和极小值;tmax，tmin为时间的极大值和极小值;通过对目标(1)优化，进行抽样获得成本的极大值和极小值，以同样的方式获得时间的极大值和极小值，此处的极值由抽样获得，并非实际中的极值.

2.2 SA算法具体过程

步骤1初始化

初始解的选择:随机产生可行解X(枢纽选择方案和分配方案)作为初始解，利用条件最短路径算法分别获得成本f1和时间f2的函数值;对数据进行标准化，获得综合目标函数f=ωf1+(1－ω)f2值，其中0≤ω≤1.

初始温度的选择:根据多次运行结果，选择与综合目标函数值具有相同数量级的数作为初始温度T0;取初始最优解 X*=X，初始状态 X(0)=X，i=p=0.

步骤2单一温度下的内部循环

在温度T=Ti下，以T，X*，X(i)为当前温度、局部最优值和当前状态值进行内部循环.

(1)令k=0时的初始当前状态为X'(0)=X(i)，初始最优解为X*'=X*.

(2)由状态X得到该情况下的枢纽集合H，分配情况Xij，进行如下步骤随机产生新的状态X'，计算增量Δf'=f(X')－f(X).①枢纽邻域搜索:随机选择节点i∈N，若i∉H，则令H=H∪{i}(新增一个枢纽);若 i∈H，且|H|≥2，则令 H=H － {i}(关闭一个枢纽).②分配方案邻域搜索:随机选择一个节点 i∈M，j∈H，若 Xij≠1，则令 Xij=1，即为该分拨中心 i添加枢纽 j;若 Xij=1，且 Σj∈NXij≥2，则 Xij=0，即为该分拨中心i减少枢纽j.

(3)若Δf'＜0，则接受新解 X'，并判断是否f(X*')＞f(X').若是，则令 X*'=X'.如果 Δf'＞0，则以概率exp(－Δf'/T)接受状态X'作为下一个当前状态.如果 X'被接受，则 X'(k+1)=X';否则X'(k+1)=X'(k).

(4)令k=k+1，判断是否k＞步骤2.若是，转入步骤2的第(5)小步;否则转入步骤2中第(2)小步的第①小步.

(5)将当前最优解X*'和当前状态X'(k)返回到改进退火过程，即转入步骤3.

步骤3判断是否f(X*)＜f(X*').若是，令p=p+1;否则令 X*=X*'，p=0.

步骤4降温Ti+1=update(Ti)，令i=i+1.

步骤5判断是否p＞步骤1或者T＜Tend.若是，转到步骤6，否则返回步骤2.

步骤6以最优解X*作为最终解输出，停止算法.

3 算例

3.1 算例的基本数据

给定10 个节点 S={1，2，…，10}，求解由这些点构成的轴辐式快递网络.已知节点之间的快递量、路段单位运输成本、路段运输时间和节点之间的运输时间限制分别见表1，2，3和4.其中:设路段的固定成本fij为定值;节点的单位分拣费用sk=10，k=1，2，…，10;单位中转成本 gk，k=1，2，…，10，分别为10，8，6，8，7，7，9，8，5，8.对这 10 个节点形成的轴辐式快递网络进行枢纽选址和分配优化.

表1 快递量Q矩阵 件

表2 路段运输单位变动成本cuv 元

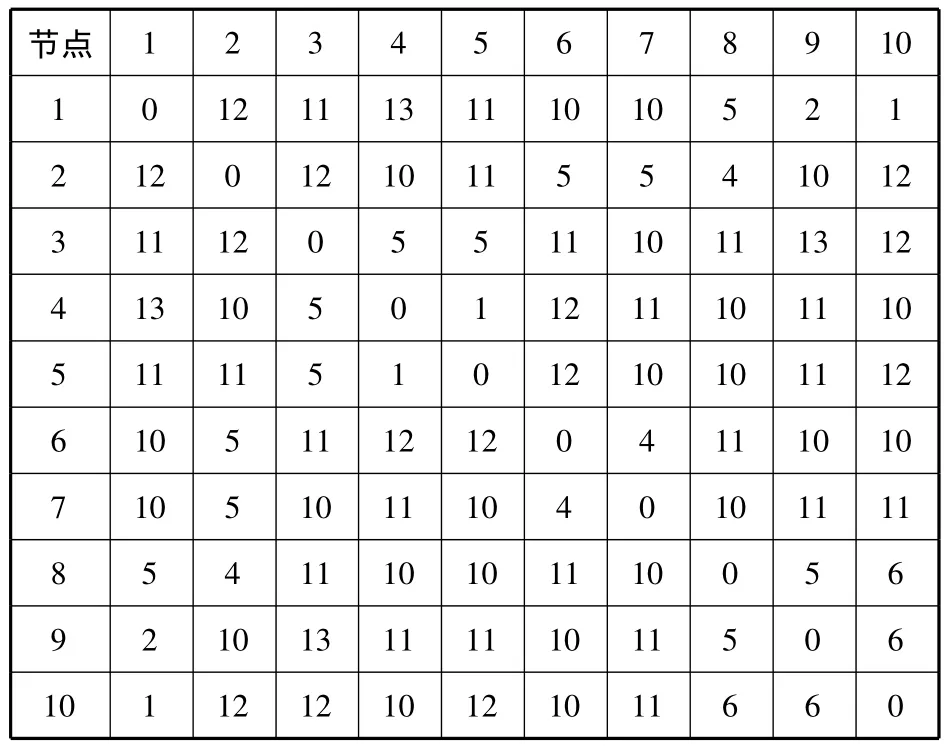
表3 路段运输时间tuv h

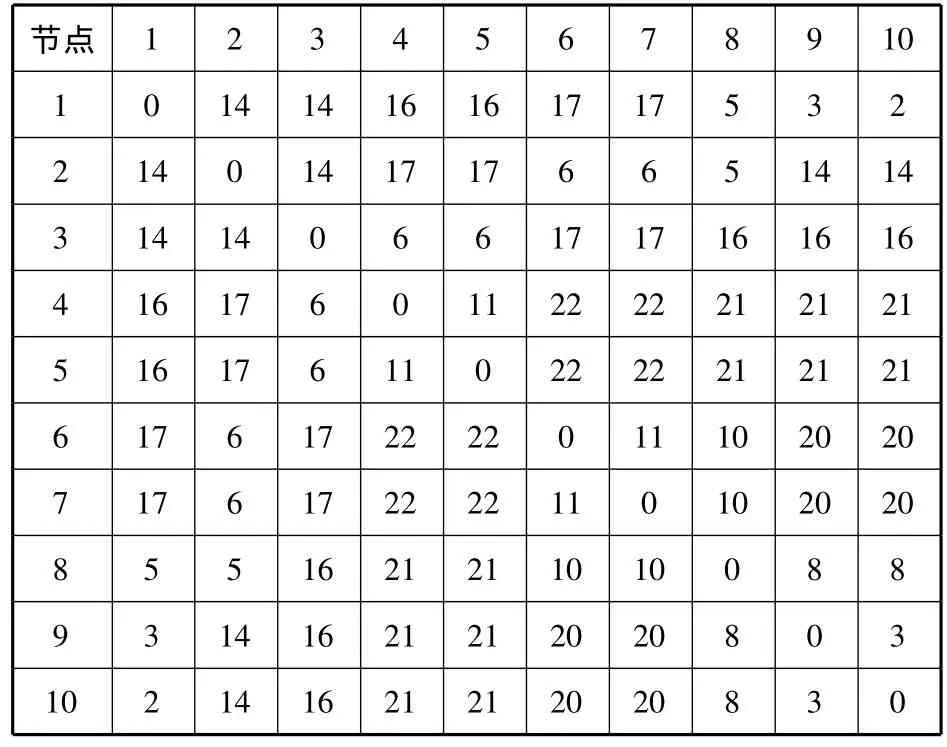
表4 节点之间的运输时间限制Tuv h

3.2 SA算法参数设置

基于第2.2节算法设计过程，用C++软件实现文中的SA算法，具体参数设置:初始温度为100 000℃;采用按比例下降的方式，温度下降比例为0.95;内部循环结束条件为同一温度下迭代次数为300次或者局部最优解在50次迭代内不改进;外部循环结束条件为温度下降至0.5℃或者全局最优解在50次循环内不改进.

3.3 运行结果及分析

设模型中折扣率α为一定值，取不同的折扣率，对应的成本值和时间值如何变化;进行综合目标评估时，权重ω取值不同，获得的可行解如何变化.对此进行以下3个分析(运行结果中成本单位为元，时间单位为h，均为非标准化的原始数据类型):

(1)探究折扣率α和权重ω的取值不同时所得到的可行解和枢纽情况.结合快递运输业的实际情况，折扣率一般取值为0.8，考虑3种水平下的固定折扣率为0.8，0.6和0.4，得到结果见表5.

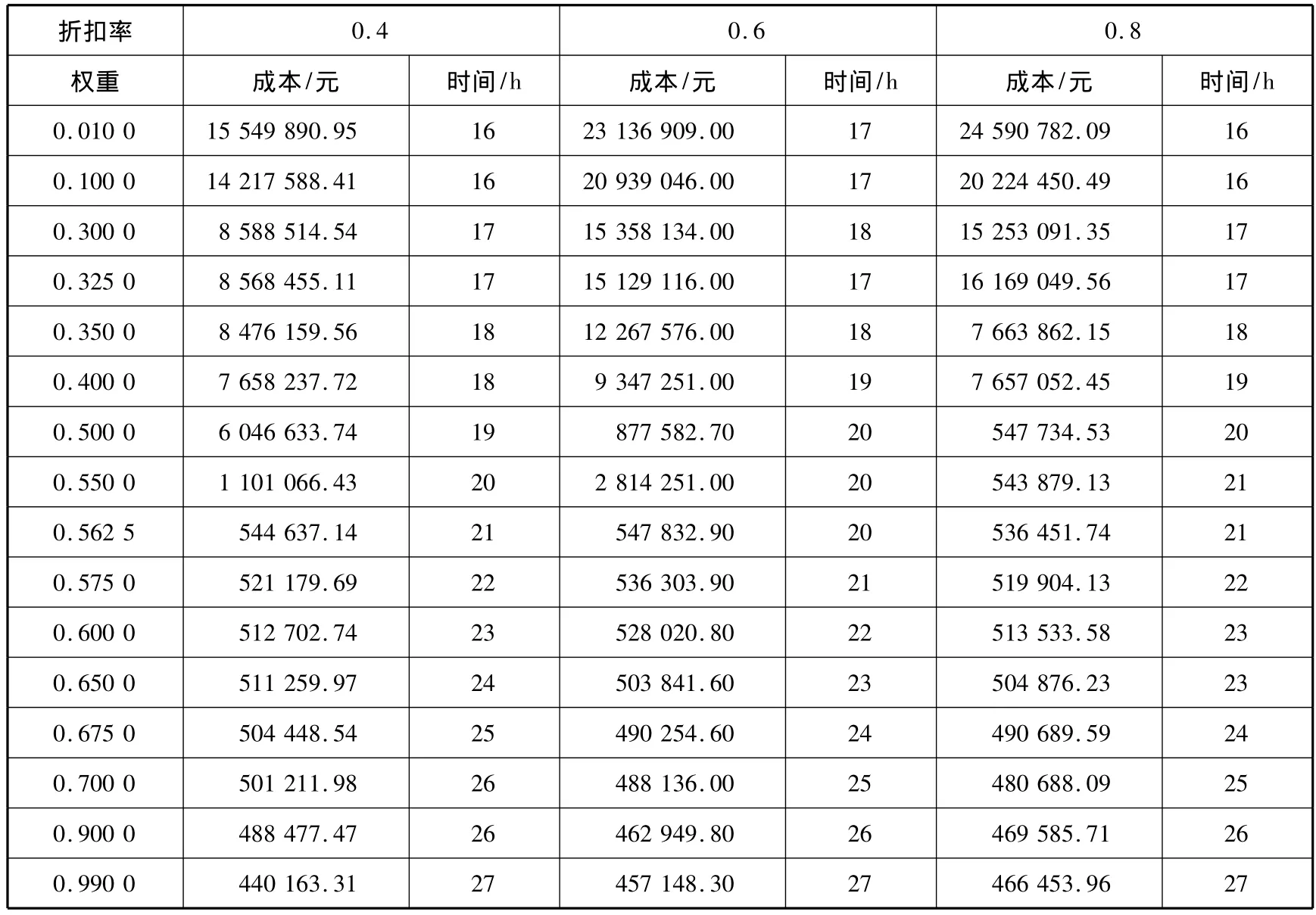
表5 不同折扣率和不同权重对应的可行解

表5中的权重值为成本函数的权重，由结果看出:在同一折扣率下，随着权重的增加(成本函数的权重值增大)，Vc降低，但是时间值增加;其中对于权重的取值，采用二分方法，对于成本值相差较大的权重进行细分.

折扣率为0.4，权重大于0.562 5时成本下降较快，而时间并没有显著增加，此点为突变点;折扣率为0.6时，突变点也为0.562 5;折扣率为0.8时，突变点为0.5.

通过算例模型求解分析由10个节点组成的快递网络:在同一折扣率下，如果取P(枢纽个数的上限)为6，7，8时，可行解所对应的枢纽个数均为5.设定P值为5，表6中列出的数据为不同权重对应的枢纽选择情况.其中当折扣率为0.8时，在不同权重下，节点1和节点2均作为枢纽点，当节点6，7，8同时作为枢纽点时，成本较高、时间较短.决策者可针对成本和时间对应的节点分别选择可行的方案.

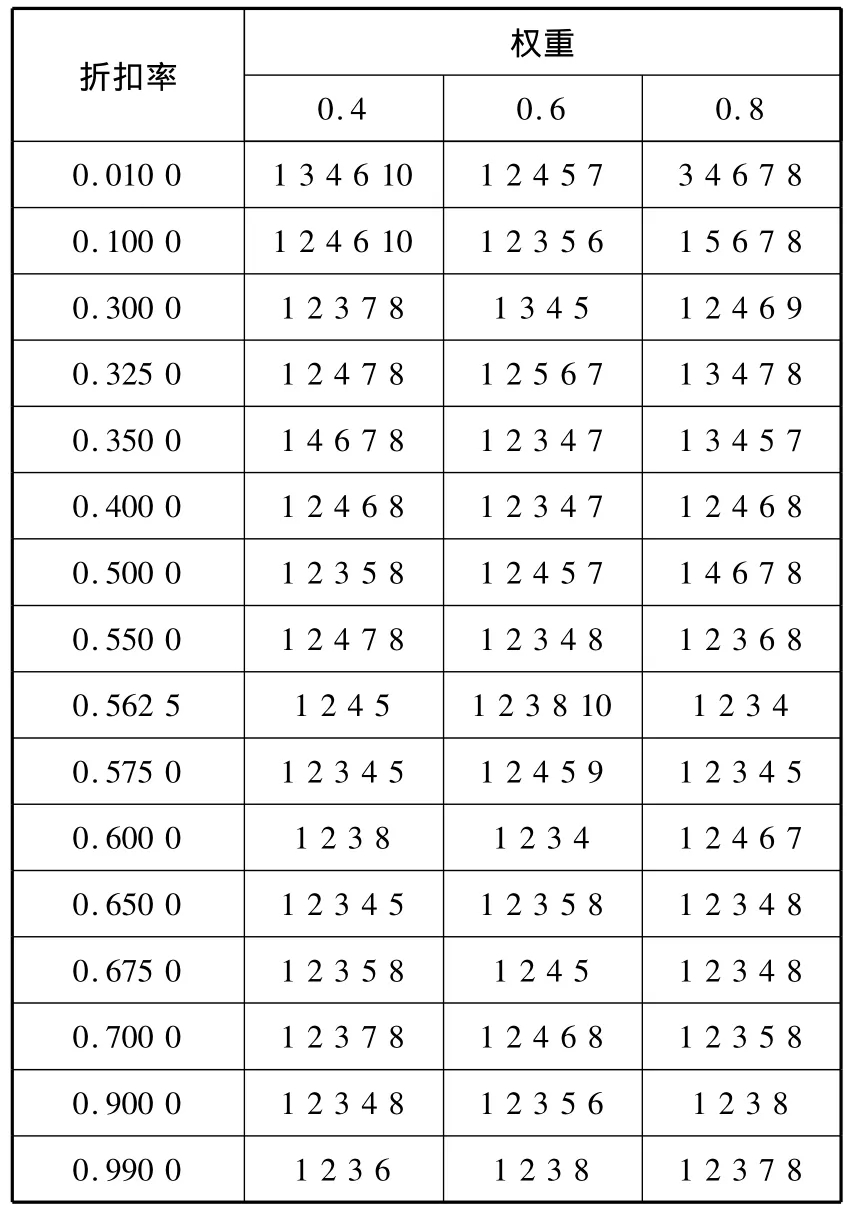
表6 枢纽个数和枢纽位置

(2)折扣率取同一值时，不同权重所获得的可行解:成本目标值和时间目标值分布.由表5中折扣率为0.8对应的数据可以看出:成本取值范围在466 453.96～24 590 782.09;时间取值范围为16～27;成本目标的取值和时间目标的取值均具有多样性.当权重小于0.325时，成本值较大，最小值为16 169 049.56元，时间最少为16 h;对比权重取0.4和0.5的情况，成本降低7 109 317元，时间仅增加1 h，为细致观察成本值和时间值的变化，考虑权重为0.50～0.99时的成本取值和时间取值情况.利用MATLAB软件，根据表5中的数据，选择折扣率为0.8时，不同权重分别对应的可行解，画出如图3所示的虚线，线上的“*”表示时间(h)和成本(元)对应的节点.其中，点 (543 879.13，12)与(53 451.74，12)的时间值相同，保留成本较小的点(53 451.74，12);(513 533.58，23)与(504 876.23，23)也有相同的时间值，也保留成本较小的点.

(3)轴辐式快递网络设计.选择折扣率α为0.8，权重ω取值为1的情况，进行轴辐式快递网络枢纽选址与分配优化，并探究快递量对网络结构的影响.求解模型得到最小成本值为396 926.18元，时间为27 h.其中节点1，2，3作为枢纽点，其余节点为非枢纽点，形成的轴辐式网络见图4.

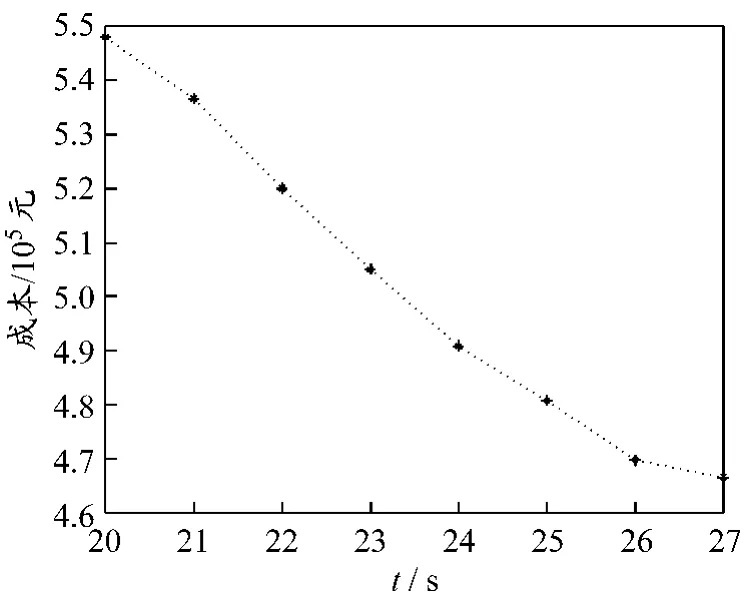
图3 帕累托最优前沿面

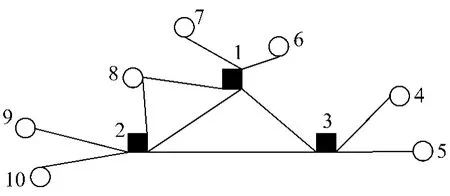
图4 成本最低的轴辐式快递网络

快递量对网络结构的影响:将节点1与节点8之间的快递量由140件减为10件，其他条件不变，形成的轴辐式网络:枢纽点仍为节点1，2和3，不同点是节点8此时仅与枢纽2相连，形成单分配轴辐式网络.分析其原因:改变节点1与节点8之间的快递量之后，如果仍然沿着路线1－8，所需费用为10×6+900+10×ln 2(增加固定路线成本f18)，而路线1－2－8所需的费用为330.显然，经过转运的成本更低，因此形成单分配轴辐式网络，体现快递量对快递网络结构的影响.

4 结束语

从多目标优化角度，研究轴辐式快递网络配置的优化问题.由于问题的 NP难性质，设计基于Floyd算法的SA算法，其中的搜索策略由枢纽邻域搜索和非枢纽邻域搜索两部分完成，以保证搜索的全局性，避免局部搜索的限制.引用10个节点的算例，分析不同折扣率下，不同权重对应的可行解和枢纽个数、位置情况.选定折扣率为0.8，用MATLAB将可行解的分布用图的形式表示出来，分析表明求解出的成本和时间取值均具有多样性.通过改变节点之间的快递量，分析快递量对轴辐式快递网络结构的影响.文中建立的多目标轴辐式快递网络模型以及求解分析，为决策者提供决策支持，使其根据成本和时间的权重分配，在有限的成本资源下，选择合理的快递网络设计方案，满足中转货物的时效要求.

［1］倪玲霖，史峰，方晓平，等.全连通快递网络与轴辐快递网络的比较［J］.系统工程，2009，27(12):45－50.

［2］YAMAN H.Star p－hub median problem with modular arc capacities［J］.Computers ＆ Operations Res，2008，35(9):3009－3019.

［3］YAMAN H，KARA B Y，TANSEL B C.The latest arrival hub location problem for cargo delivery systems with stopovers［J］.Transportation Res:B，2007，41(8):906－919.

［4］TAN P Z，KARA B Y.A hub covering model for cargo delivery systems［J/OL］.Networks，2007，49(1):28－39.［2011－04－25］.http://onlinelibrary.wiley.com/doi/10.1002/net.20139/abstract.

［5］COSTA M G，CAPTIVO M E，CLIMACO J.Capacitated single allocation hub location problem－A bi－criteria approach［J］.Computers ＆ Operations Res，2008，35(11):3671－3695.

［6］张健.公路快速货运轴辐式网络运载规划研究与应用［D］.济南:山东大学，2008.

［7］O’KELLY M E.A quadratic integer program for the location of interacting hub facilities［J］.Eur J Operational Res，1987，32(3):393－404.

［8］盛丽俊，周溪召.带有时间窗的车辆路径问题优化［J］.上海海事大学学报，2007，28(4):64－67.

［9］白治江，刘广钟.递归式多目标遗传算法［J］.上海海事大学学报，2007，28(2):62－64.

［10］SINGH H K，RAY T，SMITH W.C－PSA:constrained Pareto simulated annealing for constrained multi－objective optimization［J］.Inform Sci，2010，180(13):2499－2513.

［11］倪玲霖.轴辐式与点对点及组合式的快递网络特征分析［J］.统计与决策，2010(20):59－61.

［12］王凌，郑大钟.基于Cauchy和Gaussian分布状态发生器的模拟退火算法［J］.清华大学学报，2000，40(9):109－112.