中长期水文预报的模型辨识及预测研究*

路剑飞，于吉涛，陈子燊

(1 中山大学地理科学与规划学院水资源系,广东 广州 510275; 2 河南理工大学测绘与国土信息工程学院,河南 焦作 454000)

水文预报对于水库调度、防洪灌溉和发电等工作至关重要。按照预报的时间尺度的不同，水文预报可以分为短期预报和中长期预报，一般将预见期为3天到一年的成为中长期预报，3天以下的作为短期预报[1]。对于中长期水文预报而言，一般可以结合天气学、天文地球物理因素方法及统计学方法进行研究，相应的预报模型可大致分为过程驱动模型方法和数据驱动模型方法两大类[2]。过程驱动模型是在对水文现象的发生机理较为明晰的前提下对径流的产流过程与河道演进过程进行模拟，从而进行流量过程预报的数学模型；而数据驱动模型则是基本忽略水文过程的内在机理，通过对所研究系统多次测量得到的输入输出数据进行最优数学建模，进而达到预测的目的。

时间序列模型是数据驱动模型的一种，按模型中包含的时序数目的多少，可相应分为单变量模型和多变量模型。单变量模型以自回归滑动平均(ARMA)及其衍生类型最为常见，由于其只依靠单一时序的历史数据进行建模，对数据的依赖性小，且能给出明确的模型表达式，因此即使在各种非线性时序模型(如神经网络模型、模糊数学方法和灰色系统模型等)迅速发展的现阶段，其仍具有十分重要的作用。Holger等[3]经过研究证明，线性预测方法由于其模型的稳健性，往往会取得比非线性方法更好的预测效果。非线性方法(以神经网络为例)虽然在建模拟合阶段可以取得更好的拟合效果，但是在预测阶段往往会产生异常的预测值，且无法给出显式的表达式。

在应用ARMA模型进行系统辨识之前，有几点需要注意：① 由于ARMA模型是基于时序平稳的基础之上的，因此当时序表现出明显的周期性或均值、方差不平稳时，一般通过预处理将其平稳化。然而平稳化可能会导致模型预测精度大大降低；② 建模数据问题，用于建模的数据量过少时，所建立的模型不足以反映系统的内部特点，而当参与建模的数据过多时，会导致建立的模型过于复杂，从而增加了建模的复杂性和模型的不稳定性。因此为了得到合理的结果，应注意参与建模的数据量问题；③ 建模的方式：这里指的建模方式包括固定建模和滑动建模两种。如果用于建模的数据的代表性足以反映系统的内部特点，同时系统是定常的，则固定建模方式可以在获得合理的预测结果的同时节省大量的时间；而当系统具有明显的时变特点时，固定建模则不能很好的反映这种时变性，因此应采用滑动建模，利用更新的观测数据对系统的模型进行在线更新。而当模型较为复杂、建模所需数据量较大时，滑动建模方式往往会导致建模耗时和数据存储问题出现。本文主要结合以上思路对径流中长期预报问题进行研究。

1 流域概况及研究数据

西江发源于云南省境内的马雄山，为珠江水系的主干河道。由于从上游源头至下游各河段名称不一，狭义上西江指的是其位于广西梧州市纳入桂江后的部分，全长约为208 km，在广东三水市思贤滘与北江汇合后流入珠江三角洲网河区。每年的4-9月是西江流域降水的集中期，其中前3个月主要受到锋面和低压槽影响产生暴雨，而7-9月份则以台风影响为主，洪涝灾害等多发生在6-8月。西江干流的高要站位于思贤滘上游44 km处，上接广西梧州，下连广东大珠三角经济区，是西江中、下游的国家级重要控制站。本文采用的研究数据即为广东省西江干流高要站1960-2009年共50a的月径流数据。

2 研究方法及分析

2.1 数据预处理的影响

为了检验数据预处理对模型预测结果的影响，首先建立一组对比序列T1和T2。T1序列为仅进行标准化预处理的径流序列；由于原始月径流序列具有显著的年周变化，因此，T2为T1滤除年周变化后标准化得到的序列，其中滤波公式表示为：

(t=1960,1961,…,2009；τ=1,2,…,12)

式中t为年份，τ为月份。μτ和στ分别为对应月份的均值和标准差。T1和T2序列的时序图见图1。

在利用时间序列模型(此处指的是ARMA模型)进行系统辨识时，首先要考虑的是模型的定阶问题。序列的自相关函数(ACF)描述了在同一个过程中相距k个时滞的yt和yt+k之间的协方差和相关性；而偏自相关函数(PACF)则衡量了除去yt和yt+k共同依赖的干预变量yt+1,yt+2,…yt+k-1的影响后的相关性，因此根据序列的ACF和PACF可以对系统模型进行有效辨识。图2分别给出了T1和T2序列用于建模的前480个点(40a)的ACF和PACF图。

由图2可知，T1序列的ACF呈阻尼正弦波动拖尾，PACF也属于阻尼正弦波动拖尾，因此适用于ARMA模型[4]；T2序列的ACF呈现指数衰减，而PACF为1步截尾，因此适用于AR(1)模型。为了进一步进行检验判断的合理性，本文针对实际水文序列样本长度有限的特点，利用结合有限采样理论的组合信息准则(CIC)作为模型优选的判断准则[5]。由此得到两个时序的模型分别为：

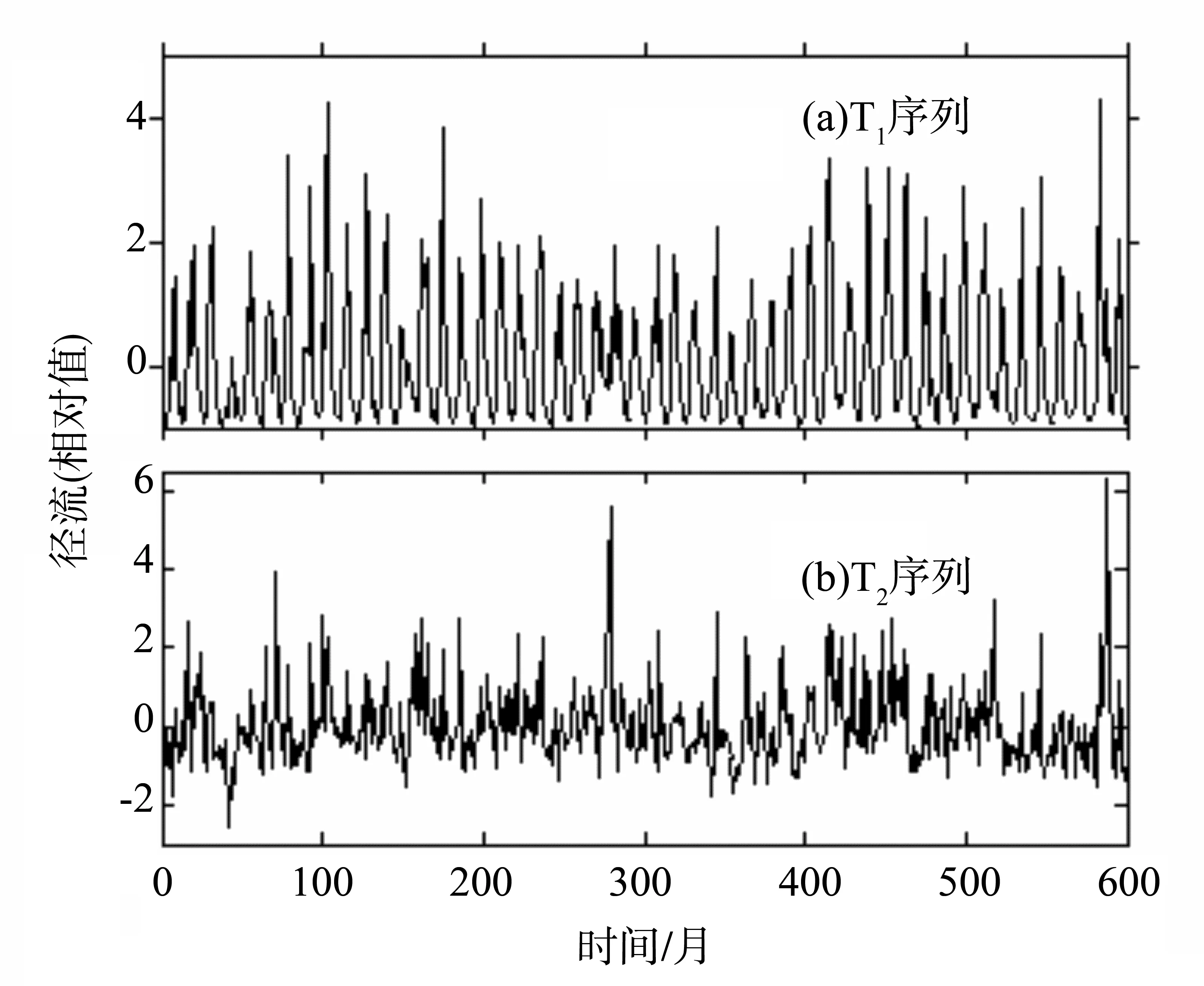
图1 T1和T2时序图

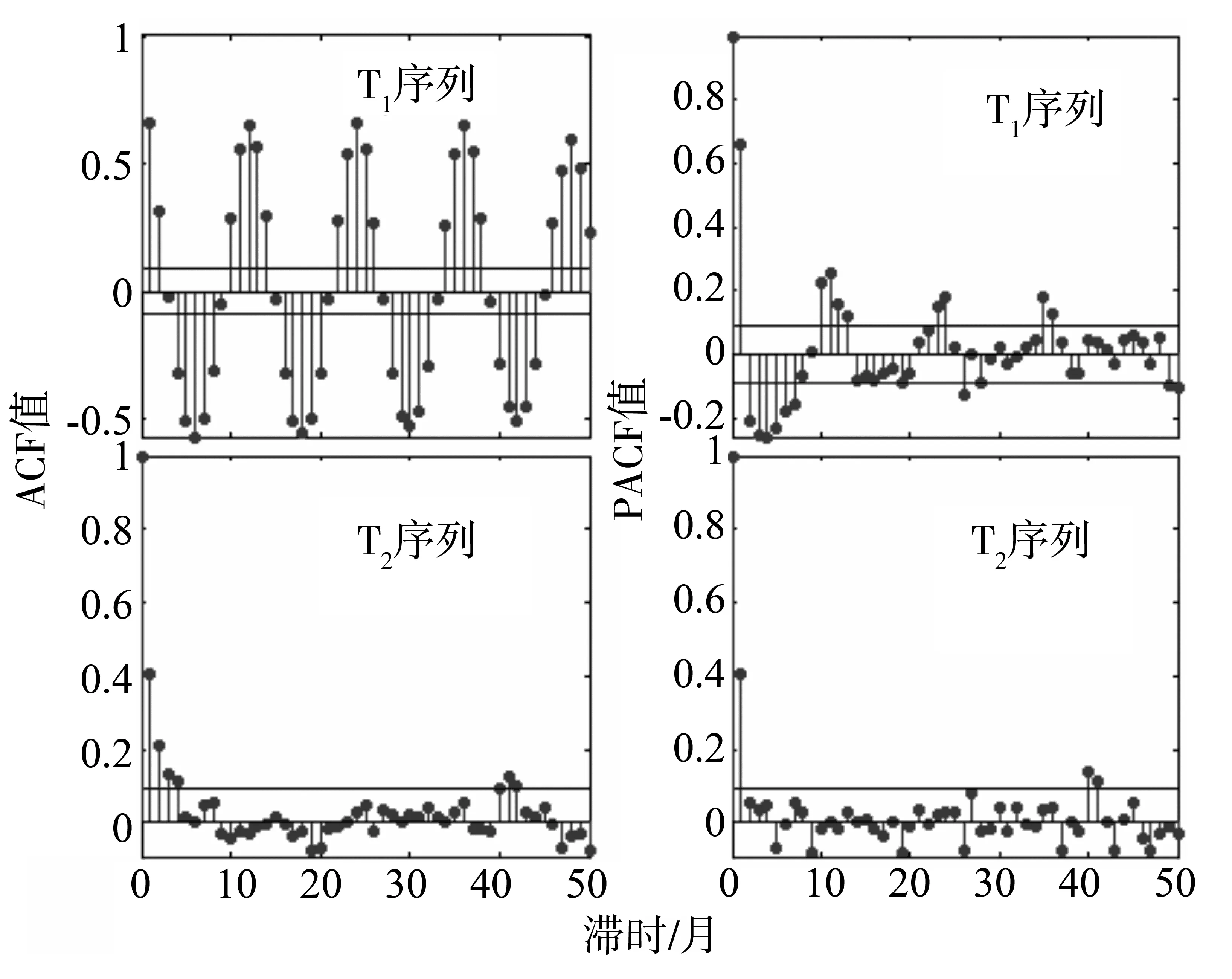
图2 T1和T2的ACF和PACF图

T1(k)=-0.51T1(k-1)+0.209

T1(k-2)+…-0.0989T1(k-13)+q1(k)

+0.8624q1(k-1)+0.0989q1

(k-2)+…-0.7509q1(k-12)

T2(k)=0.4038T2(k-1)+q2(k)

其中，q1和q2分别为各自模型的新息(innovation)值。由上式可知，T1∈ARMA(13,12)；T2∈AR(1)，其与ACF和PACF的判断结果一致。为了检验两个模型的预测性能，图3分别给出了两者的预测结果。

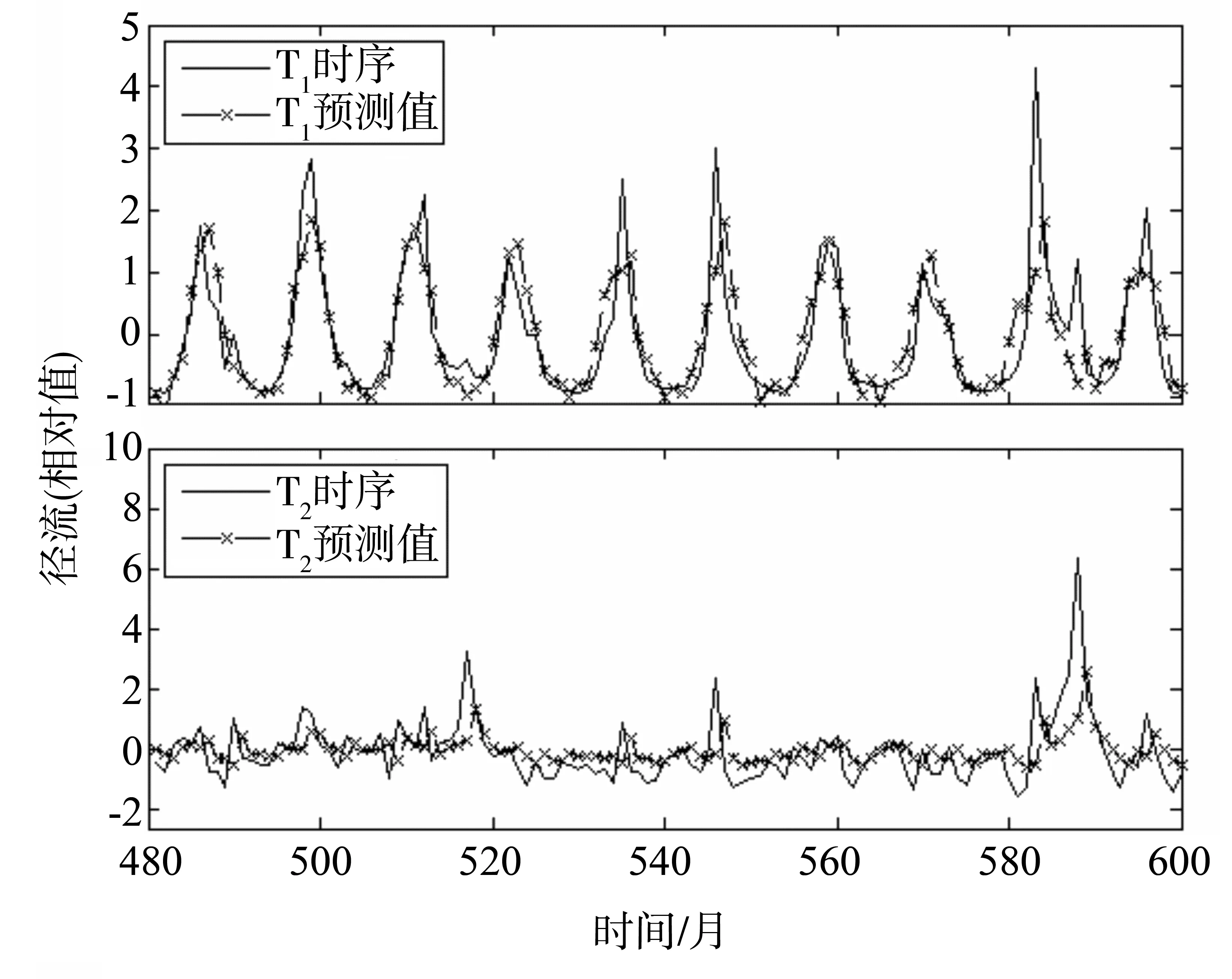
图3 T1和T2模型的预测图

通过对比可以看出：由于预处理的影响，使得T2序列的模型辨识结果由ARMA(13,12)降为AR(1)，复杂性大大降低，从而影响其预测性能，使得预测结果存在明显的滞后现象，且当径流值较小时，预测误差显著增大。因此在进行模型辨识时，预处理过程一定要慎重，尤其是当预处理导致识别的模型复杂度大幅度降低时，应通过模型的预测结果对预处理方法的合理性进行检验。

2.2 建模数据量的影响

在进行模型辨识时，建模的数据量对于模型的预测精度影响很大。理论上用于建模的样本量要足以反映时序的内在波动性，才能获得较好的预测结果。但建模数据过多也会导致模型的复杂性和计算耗时增加。因此有必要对建模的合理数据量进行研究，评价依据为模型预测误差的均方差。而建模的方式(固定建模和滑动建模)对模型的预测性能同样构成影响。固定建模即对时序的前n个数据进行建模，对余下的数据进行预测检验；而滑动建模则是利用新的观测值对模型进行在线更新。当系统为定常离散系统时，两种建模的效果是一样的，而当系统的时变性较强时，固定建模不足以体现系统的时变性，理论上采用滑动建模方式更能追踪系统的时变特征。两种建模方式均可表示为[6]：

T(k)=φ1T(k-1)+…+φpT(k-p)+a(k)-

θ1a(k-1)-…-θqa(k-q)

其中，φi(i=1,…,p)和θj(j=1,…,q)分别为AR模型和MA模型的系数；p和q分别为相应模型的阶数，可利用文献[5]中的方法进行求解。两种建模方式的根本区别在于：固定模型仅进行一次定阶和求解系数，之后单纯的根据输入计算输出；而滑动模型采用的是滑动定阶和求解系数，系数随着时间的推移是变化的。图4给出了不同建模数据长度下2种建模方式的预测误差的MSE曲线图。

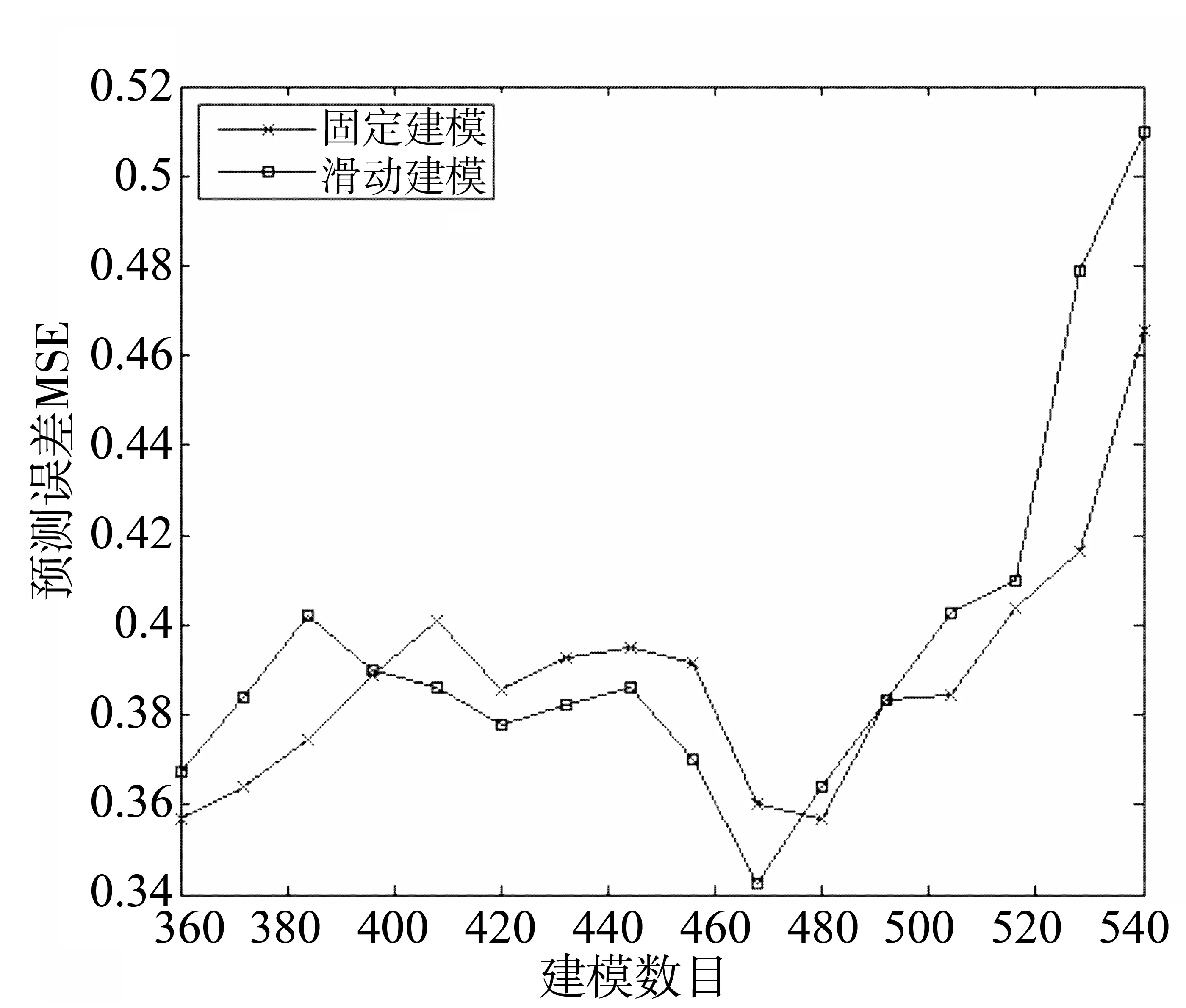
图4 模型预测误差曲线

由图4可知，当建模的数据量在360～540之间变动时，滑动建模并不总是优于固定建模方式。当建模数据量为468(39a)时，采用滑动建模方式可以得到最优的预测效果。此时继续增加建模数据量，反而会使滑动建模的预测效能不断降低。当建模数据量大于480(40a)时，固定建模方式的预测效果将超过滑动建模方式。图5给出了当建模数据量为468时，两种不同建模方式的预测效果，为了便于比较，图6进行了进一步处理。图6中横轴表示预测的相对误差，纵轴表示低于某一预测相对误差条件下的预测结果数占总预测数的百分比。由此可知：在同一相对误差约束条件下，总体上滑动模型的预测效果要好于固定模型。而当径流处于较低值(<1 500 m3/s)和较高值(>5 000 m3/s)时，滑动模型预测的相对误差均小于固定模型(具体见图7)。

2.3 建模方式的影响

通过上述研究可以发现：当将月径流系统作为线性定常离散系统进行建模预测时，预测结果可以很好的反映径流的变化趋势，对于径流的中长期变化趋势可以给出准确的指导，同时可以给出明确的表达式。其不足之处在于，对峰值的拟合效果较差，当预测相对误差阈值定为40％时，即使是滑动建模方式也仅有60％的预测结果符合标准；随着径流值的提高，预测的平均相对误差不断减小，但最小值仍接近40％。因此当所要求精度较高时，以上的两种建模方法均不足以胜任。

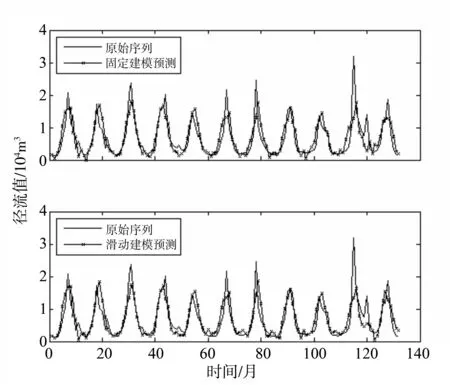
图5 不同建模方式的最优预测结果图

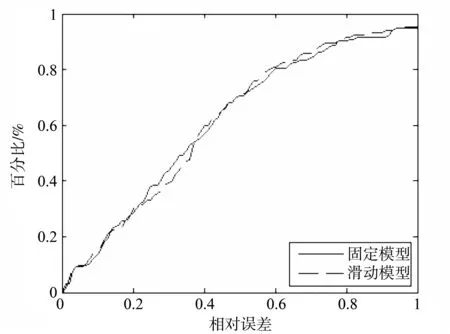
图6 模型预测相对误差分布图

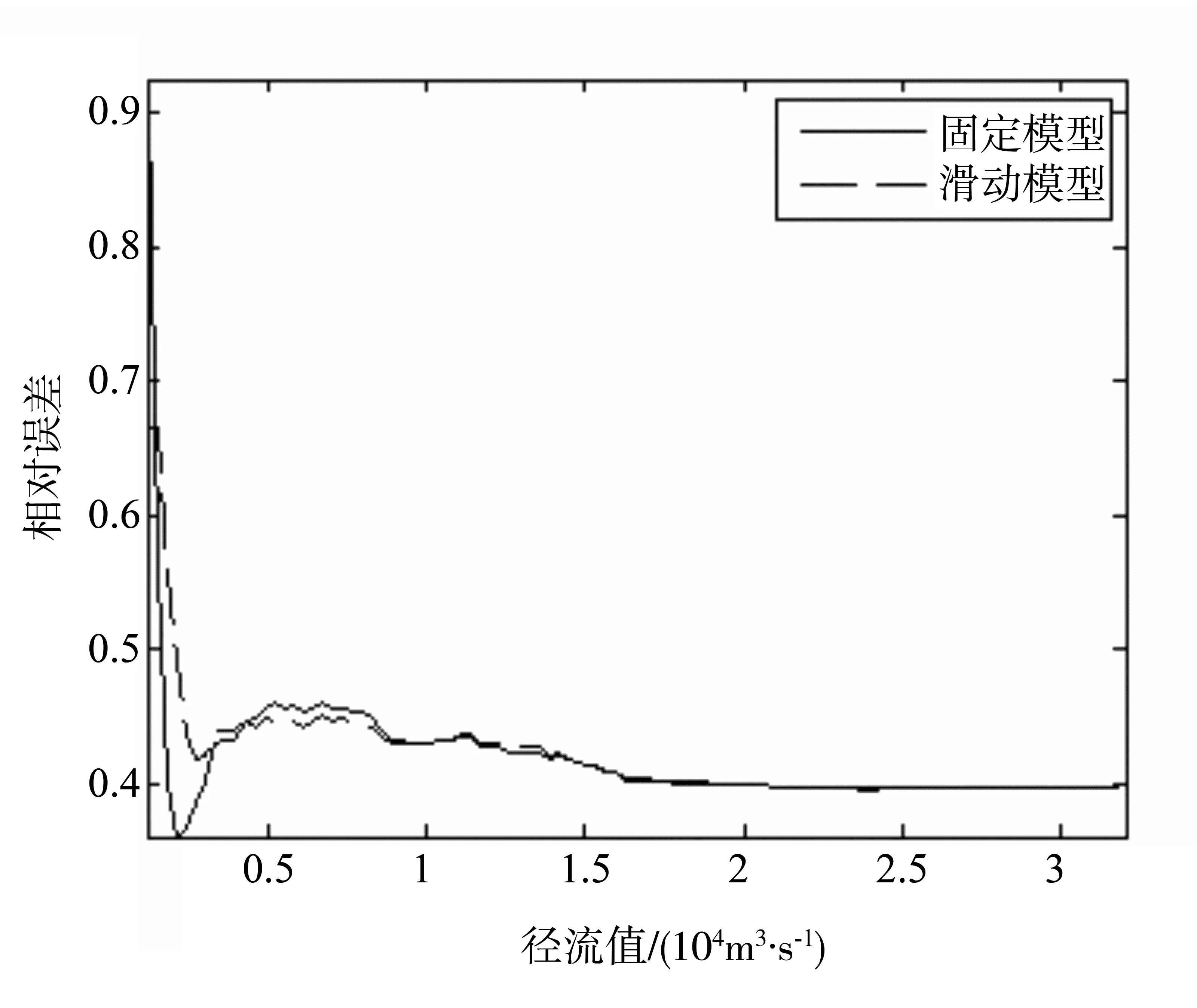
图7 模型预测性能曲线

在模型辨识中，当系统的时变性较强时，往往需要根据不断更新的数据进行重新辨识以追踪系统的时变特征，滑动建模即是基于这一思路。而当模型较为复杂、建模所需数据量较大时，滑动建模方式往往会导致建模耗时和数据存储问题出现。近年来兴起的神经网络、遗传算法等现代辨识手段由于具有良好的非线性逼近能力、容错性、推广能力和自学习特性被广泛应用于非线性系统时间序列的预测与分析中。但是，这些方法本身存在大量的理论问题尚待说明，所建模型缺乏可靠的数学表达形式，而且很难找到有效的学习算法，容易陷入局部极值。

状态空间描述则很好地避免了这一问题的出现，其思路在于将“输入-输出”过程描述为“输入-状态-输出”过程，通过建立动态系统的状态空间方程来描述系统的定常(时变)特征。当系统的时变性较强时，只需要对状态向量进行在线更新即可，具有高度的灵活性，同时状态空间描述并不要求输入或输出过程为平稳过程[4]。Kalman滤波是基于系统状态空间描述的一种最优滤波技术，可以解决非平稳和矢量估计问题[7]，其递推计算形式能够适应实时处理的需要，不需要存储大量的数据，所以经常用于非线性离散系统的参数辨识及预测研究中。其针对的离散系统的状态空间模型一般表示为[8]：

式中，xk，yk分别为k时刻的状态向量和输出向量；qk-1为k-1时刻的系统噪声，rk为k时刻的测量噪声，且有qk-1～N(0,Qk-1)，rk～N(0,Rk)，假定两个噪声彼此独立。Ak-1为k-1时刻的状态转移矩阵，由控制对象的参数决定；Bk-1为k-1时刻的激励转移矩阵；Hk为k时刻的输出转移矩阵；Dk为k时刻的直接传输矩阵。上式的递推更新方程可使用不同的方法得到，本文采用文献[9]的方法进行求解

本文首先利用ARMA模型对月径流序列进行建模，由之前的研究得出，最优建模长度应为468(月)，利用CIC准则进行模型定阶，得到ARMA(13，12)模型：

y(k)=0.5666y(k-1)-0.1095y(k-2)+

…+0.0702y(k-13)+q(k)

-0.2077q(k-1)-0.0317q(k-2)+

…-0.2232q(k-12)

然后将其转化为状态方程形式[6]：

利用得到的状态空间模型，结合Kalman滤波方法进行预测，结果见图8。

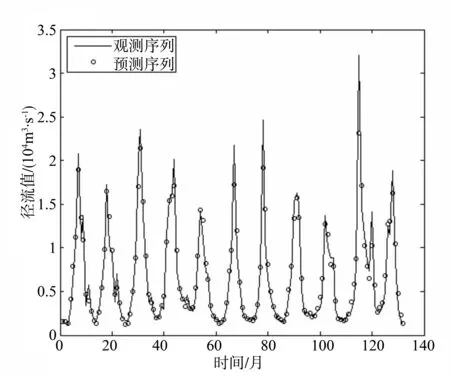
图8 Kalman滤波预测图

由图8可知，运用Kalman滤波方法预测得到的峰值和实际情况十分吻合，仅在幅度上稍有差异。进一步对比图6-9可以发现：当相对误差阈值设定为20％时，合格率由之前的30.3％提高到73.5％；而阈值为40％时，准确率则由之前的60.0％提高到94.7％。在不同的径流条件下，当径流值小于5 000 m3/s，预测的最小相对误差由41.77％降为10.04％；当径流值大于10 000 m3/s时，预测的最小相对误差由39.63％降为14.65％。由此可知，在应用Kalman滤波进行径流预测后，预测效果明显提升。

表1给出了不同径流条件下各种预测方法的预测合格率情况(即预测相对误差小于20％)。对于滑动模型而言，当径流值大于2 000 m3/s时，其预测效果要优于固定模型，其峰值预测准确率比固定模型要高出4.6个百分点。而当径流值小于2 000 m3/s时，固定模型则要强于滑动模型的预测效果。由此可见，滑动模型主要是改善了较高径流值和径流峰值的预测情况，相对牺牲了较低径流值的预测精度。而Kalman滤波方法则全方位、大幅度的提高了径流在各个区段的预测效果，其峰值预测准确率更是高达63.64％。

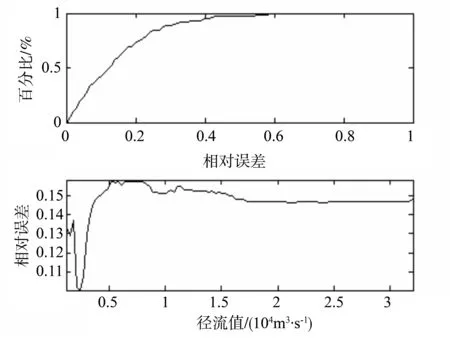
图9 模型预测效果评价图

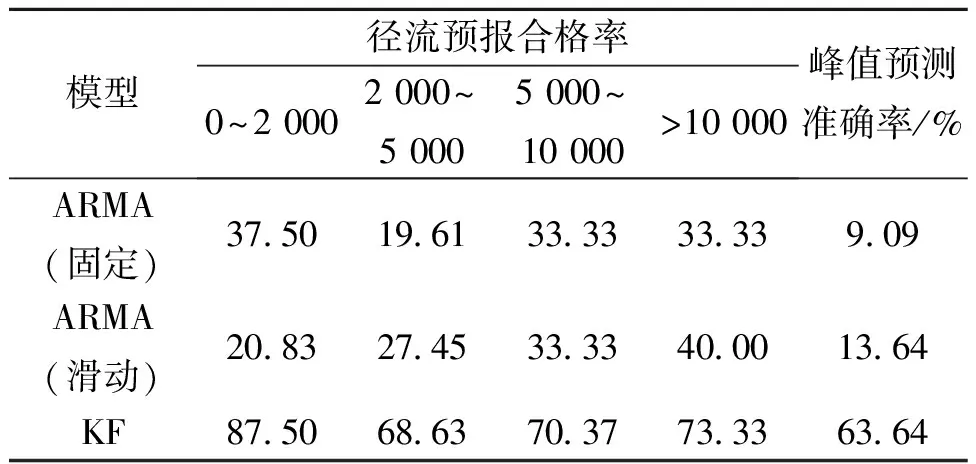
表1 模型预测效果比较

3 结 论

本文以广东省西江干流高要站50年的月径流资料为基础，针对中长期水文预报模型辨识过程中存在的问题进行研究，结果表明：

1)在进行模型辨识时，预处理过程的不同可能导致所辨识模型的复杂程度发生较大改变，应通过模型的预测结果对预处理方法的合理性进行检验；

2)建模数据量应足以反映时序的内在波动性，而过多的建模数据量又会增加辨识模型的复杂程度，在增加计算耗时的同时，也降低了预测的稳健性；

3)滑动模型主要改善了较高径流值和径流峰值的预测情况，而牺牲了较低径流值的预测精度。两种建模方式的预测结果均可以准确的反映径流的中长期变化趋势，并给出明确的表达式。其不足之处在于，对峰值的拟合效果较差，且精度不够。

4)Kalman滤波方法能准确的预测径流峰值及其变化趋势，仅在幅值上有所差异，全方位、大幅度的提高了径流在各个区段的预测效果，其峰值预测准确率高达63.64％。

参考文献：

[1]中国大百科全书编辑委员会.中国大百科全书: 大气科学，海洋科学，水文科学卷[M].北京: 中国大百科全书出版社,1987.

[2]王文,马骏.若干水文预报方法综述[J].水利水电科技进展,2005,25(1):56-60.

[3]KANTZ H,SCHREIBER T.Nonlinear time series analysis[M].Cambridge: Cambridge University Press,1997.

[4]CHAN N H.Time series: applications to finance[M].New York: John Wiley & Sons,2002.

[5]BROERSEN P M T.Facts and fiction in spectral analysis of stationary stochastic processes[J].IEEE Transactions on instrumentation and measurement,2000,49(4): 766-772.

[6]WEI W S.Time series analysis—univariate and multivariate methods[M].2nd.Boston: Addison Wesley,2005.

[7]LUDEMAN L C.Random Processes: Filtering,Estimation,and Detection[M].Wiley-IEEE Press,2003.

[8]张德丰.Matlab控制系统设计与仿真[M].北京: 电子工业出版社,2009.