散乱数据带自然边界条件三元多项式光顺样条*
徐应祥,关履泰,许伟志
(1.中山大学新华学院,广东 广州 510520;2.中山大学科学计算与计算机应用系,广东 广州 510275)
散乱数据拟合在许多领域中都有广泛的应用[1-4]。以前考虑得比较多的是平面散乱数据拟合问题,但近年来已有不少更高维的问题出现,例如动画设计与制作,动态医学三维图像演示等方面有热烈的讨论[5]。从上世纪60年代以来,众多的科技工作者对散乱数据曲面插值问题进行了一系列的研究[6-10]。近来,Lai、吴宗敏等有一系列总结性的工作[11-14],但是对多元散乱数据与大规模散乱数据插值问题的解决一直不够理想。目前在空间散乱数据插值中用得较多的三角剖分方法很难推广到更高维去,而径向基函数方法则在计算稳定性与良好逼近性方面有欠缺,不像一元三次B-样条那样有一系列良好的性质,能很好地解决一元散乱数据插值问题。李岳生和关履泰在1989年试图推广一元三次自然样条对散乱点插值的方法到二元情形,提出散乱数据的二元多项式自然样条插值,研究了广义混合样条函数空间矩形域带连续边界条件和离散边界条件的多元散乱数据最优插值问题[15]。1993年,Chui和关履泰把二元的结果全面地推广到一般多元情形[16]。关履泰在1993年给出了一种二元散乱数据的多项式自然样条光顺[17],并在1997年研究了类似B-样条的多元局部支撑基函数[18],并于2003年发表了关于这种局部支撑基的性质及插值自然样条算法[19]。但是这类样条的目标泛函比较复杂,带有一系列的积分项,没有明显的物理意义,而且在很多情形下,如果区域边界上没有插值点或插值点太少,那么插值效果就会比较差。关履泰、许伟志和朱庆勇等研究了一类新的二元自然样条插值方法,该方法的目标泛函较为简单,没有离散边界插值点,更符合实际情况,而且结果比以前的更加简单,计算起来更加方便[20]。
Laurent[21]在其著作《逼近与优化》中推广一元三次样条的优化性质,提出Hilbert空间样条进行研究,Bezhaev等[22]其后在《样条的变分理论》中对多元Hilbert空间样条作了进一步的讨论,李岳生[4]对样条变分法的欧拉方程有进一步的分析。不论是一元还是多元Hilbert空间样条,解决问题的难点和关键都在于如何提出一个合理的目标泛函,使得用变分法得出的欧拉方程容易求解,从而能够求得问题显式的解。在动态医学图象处理,三维动画设计等实际应用问题中,出现了采样点不仅要确定三维空间中位置,而且还有时间的限制,这使得采样数据出现了4维散乱数据的情形,因此对于4维散乱数据的处理也要作进一步讨论,如怎样更有效的对4维散乱数据进行插值或光顺等。本文深入进行目标泛函的研究,提出简单合理的目标泛函进行讨论,构造出一种更符合实际的Hilbert空间三元带自然边界条件的样条。这种带自然边界条件的样条在简单情况下,即不带导数条件下是三奇次的多项式(即关于每个变元xj是2pj-1次多项式,j=1,2,3),其算子T的核是〈p1,p2,p3〉阶(见定义1)多项式空间的子空间,在一般情形下这种样条是三元多项式。用这种新的三元带自然边界条件的样条考虑4维空间散乱数据的光顺问题,则该问题的带自然边界条件的样条解与以往不同,其基函数有良好的边界条件与简单的表达式,且求解此问题时所用到的线性方程组的系数矩阵是对称矩阵,这使得求解也更为方便。虽然解在表达式上与单边基有关,但可以证明对应的系数矩阵是正定对称的,可以有较稳定的迭代算法,这些我们在以后的文章中讨论。
1 散乱数据三元带自然边界条件的光顺样条
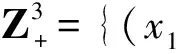
若函数u在区域Ω的边界xi=ai(i=1,2,3)满足如下的条件:
u(i1,p2,0)(a1,x2,x3)=0,u(p1,i2,0)(x1,a2,x3)=0,
u(i1,i2,p3)(a1,a2,x3)=0,u(p1,p2,i3)(x1,x2,a3)=0
(1)
其中ik=0,1,…,pk-1,k=1,2,3,则称u满足自然边界条件NB,简记为u|NB=0。记Y1=L2(Ω),令T1:X→Y1是一个从X到Y1的线性算子,定义为T1(u)=u(p)=∂pu,其中
X={u|u∈X1,u|NB=0}
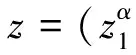
Au=(u(α)(x1),u(α)(x2),…,u(α)(xN))
其中u(α)(xi)=u(α)(x)|x=xi,i=1,…,N,k=1,2,3。对每个k有αk∈Ik,而Ik⊂Ipk={0,1,…,pk-1}都是任意指定的指标集,总指标数为q。
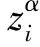
问题T 求u(x)∈X,使得如下的泛函
ρ
(2)
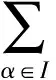
取Y=Y1⊗Q为Y1与Q的乘积空间,定义线性连续算子T:X→Y为T=T1⊗A,则问题T还可写成:
问题T1 求σ(x)∈X,使
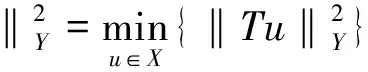
(3)
这里考虑到正数ρ的作用,定义空间Y的范数为
ρ
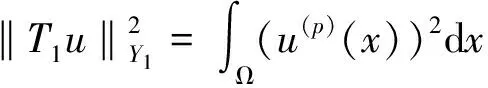
除以上问题中引入的记号外,为表示简单,后文中还需要用到如下的记号
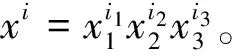
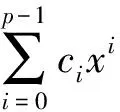
定理1 算子T1的化零子空间满足
(4)
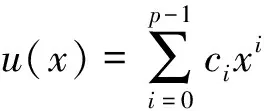
反之,如果u∈N(T1)且满足边界条件(1),则由u(p1,p2,p3)(x1,x2,x3)=0,于是有
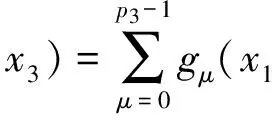
再由u(p1,p2,k)(x1,x2,a3)=0,k=0,1,…,p3-1,知
,
以及
μ(μ-1)…(μ-k+1),,
k=1,…,p3-1
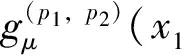
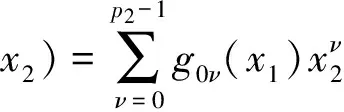
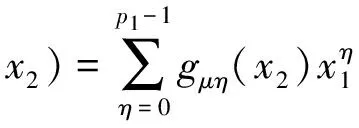
于是可推得
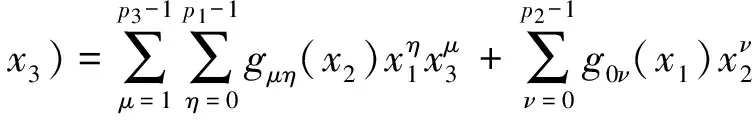
再由边界条件
u(i,p2,0)(a1,x2,x3)=0,i=0,1,…,p1-1,
u(p1,j,0)(x1,a2,x3)=0,j=0,1,…,p2-1
可知
,
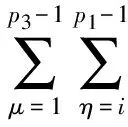
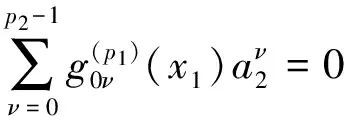
i=1,…,p1-1,j=1,…,p2-1
当a1≠0,a2≠0,时,由x3的任意性及上述各式容易解得
p1-1,ν=0,1,…,p2-1,μ=0,1,…,p3-1
于是可知
,
代入u(x1,x2,x3)的表达式,便知u可表示为
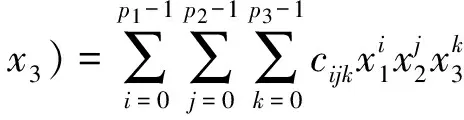
即u∈P〈p1,p2,p3〉=P〈p〉。综上可知N(T1)=P〈p〉。
定理2 算子T的化零子空间满足
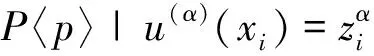
α=(α1,α2,α3),αk∈Ik,k=1,2,3,i=1,…,N}
(5)
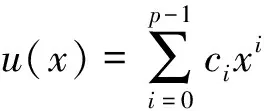
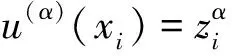
反之,如果u∈N(T),则Tu=0且满足边界条件(1)。因此T1u=0,Au=0。
一方面由T1u=0,根据定理1可知u∈P〈p〉。
另一方面再由Au=0,知
由此得
,αk∈Ik,k=1,2,3,i=1,…,N
综上两方面可知定理得证。
2 散乱数据三元自然光顺样条特征及构造
定理3 (特征定理)σ∈X是4维带自然边界条件的光顺样条的充分必要条件如下:
σ(p)(x)u(p)(x)dx+
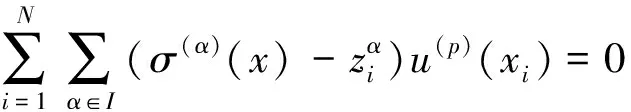
对一切u∈X成立.
证明根据定义,上式即
〈T1σ,T1u〉Y1+ρ〈Aσ-z,Au〉Q=0
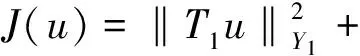
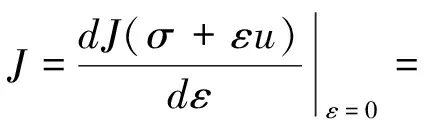
〈T1σ,T1u〉Y1+ρ〈Aσ-z,Au〉Q
因此有〈T1σ,T1u〉Y1+ρ〈Aσ-z,Au〉Q=0。
反之,若〈T1σ,T1u〉Y1+ρ〈Aσ-z,Au〉Q=0,则
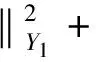
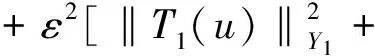
即J(u)在σ处取极小。
为了找出问题T的解,即带自然边界条件的光顺样条所具有的形式,先讨论在散乱点方型域Ω中不带导数条件时的情形,此时称问题T的解为简单带自然边界条件的光顺样条。
定理4 (构造定理) 4维散乱数据的三元简单带自然边界条件的光顺样条σ(x)是三奇次多项式且具有如下的显式及紧凑格式的表达式:
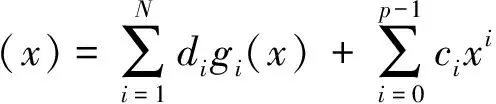
(6)
其中
,aj;xj),i=1,…,N
(7)
是三奇次样条基函数,并且有
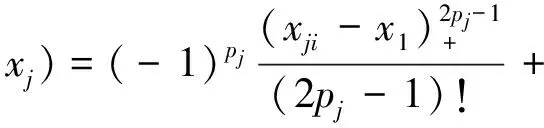
(8)
此处
(9)
kj=0,1,…,pj-1,j=1,2,3。系数cjkl及di由方程组
(10)
决定,此处D=(di)T,C=(clmn)T,矩阵E=(eij)是N×N阶方阵,且满足
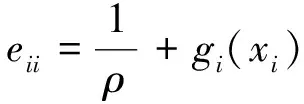
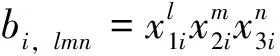
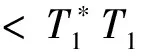
BTD=0
(11)
对任意X中的元素u,在a1点Taylor展开,有
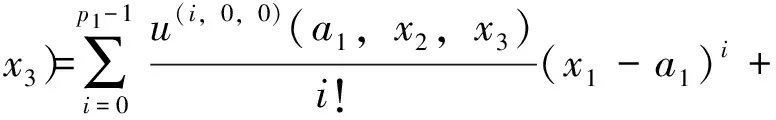
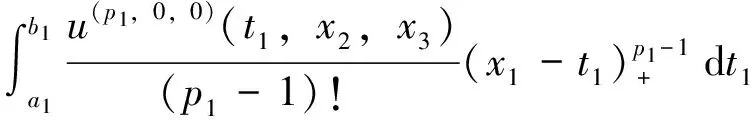
类似地,由Taylor展开还有
u(i,0,0)(a1,x2,x3)=
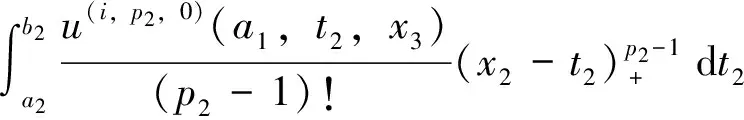
u(i,j,0)(a1,x2,x3)=
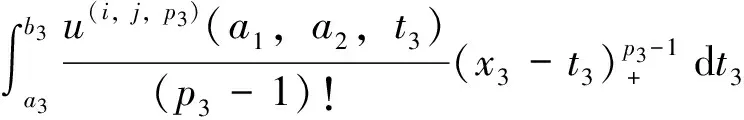
u(p1,0,0)(t1,x2,x3)=
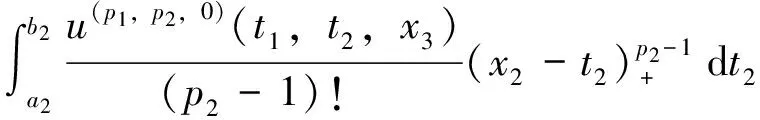
u(p1,p2,0)(t1,t2,x3)=
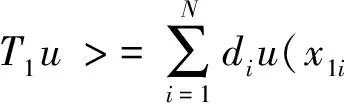
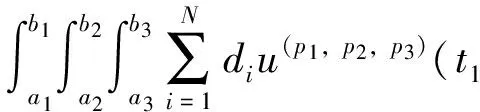
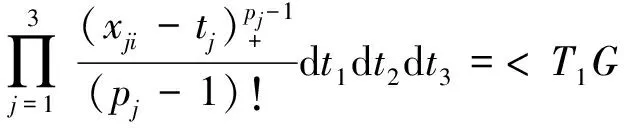
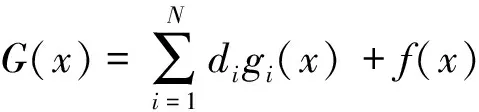
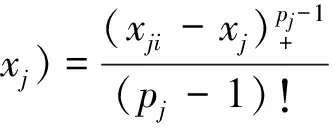
及自然边界条件(1)。所以
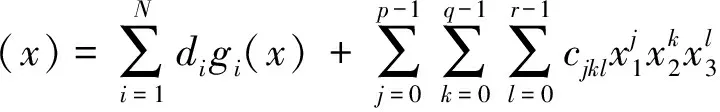
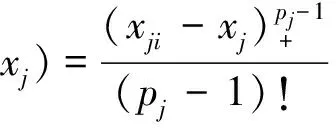
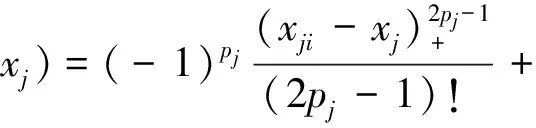
再由gi(x1,x2,x3)满足自然边界条件
,x2,x3)=0,l=0,1,…,p1-1
可知
[G(l)(x1i,a1;a1)]G(p2)(x2i,a2;x2)G(x3i,a3;x3)=0
由此有
,
l=0,1,…,p1-1
于是可得
,k=0,1,…,p1-1
类似地可得G(x2i,a2;x2)及G(x3i,a3;x3),其形式与G(x1i,a1;x1)类同,这里不再赘述。
再由特征定理可知在不带导数的简单情形下有
σ(p)(x)u(p)(x)dx+ρσ(xi)-zi)u(xi)=0
而由前述证明有
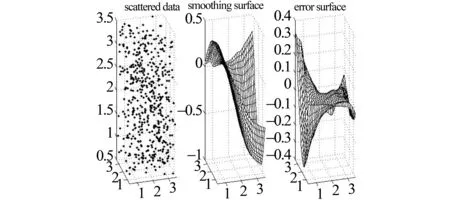
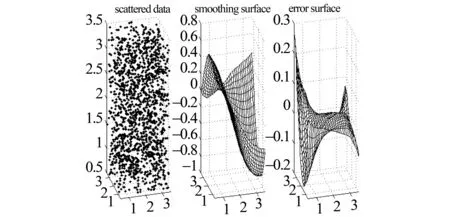
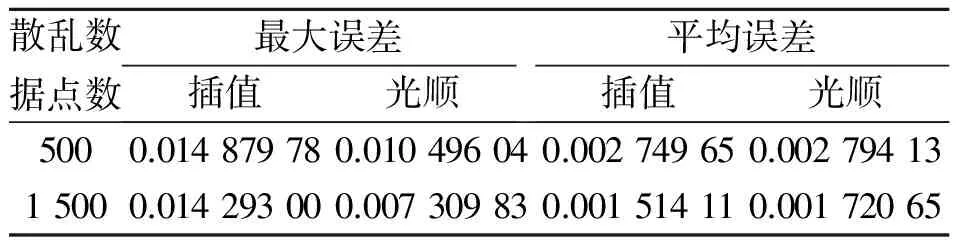
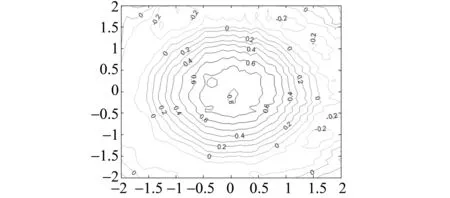
σ(p)(x)u(p)(x)dx= , i=1,…,N 这正好是方程 AD+BC=z (12) 综合式(11)、(12),定理得证。 下面用类似的方法再考虑带导数条件的一般情形,则有 定理5 (构造定理)设σ(x)是4维散乱数据的三元带自然边界条件的光顺样条,则其具有如下的显式及紧凑格式的表达式 (13) 其中 ,aj;xj),i=1,…,N (14) 是三维样条基函数,并且有 (15) 此处 (16) kj=0,…,pj-1,j=1,2,3.系数cjkl及di由方程组 (17) BTD=0 (18) 对任意X中的元素u,在a1点Taylor展开,有 u(α1,α2,α3)(x1,x2,x3)= 类似地,由Taylor展开还有 u(α1+i,α2,α3)(a1,x2,x3)= u(α1+i,α2+j)(a1,x2,x3)= u(p1,α2,α3)(t1,x2,x3)= u(p1,p2,α3)(t1,t2,x3)= 及自然边界条件(1)。所以 余下讨论与定理4类同,这里不再赘述。 例1 取三元函数 u(x1,x2,x3)=cosx1sinx2sinx3 边界取为a1=a2=a3=-0.5,b1=b2=b3=4.5,即区域Ω为[-0.5,4.5]×[-0.5,4.5]×[-0.5,4.5]。散乱数据位于[0.5,3.5]×[0.5,3.5]×[0.5,3.5],由随机函数产生。用〈2,2,2〉阶三奇次简单带自然边界条件光顺样条拟合函数u。在此仅列出当参数ρ=0.5,x3=2时,取500个散乱点和1 500个散乱点的光顺曲面图形,最大误差和平均误差(图1,图2及表1)。 表1 x3=2时的误差 图1 x3=2时500个散乱点,光顺与误差曲面 图2 x3=2时1 500个散乱点,光顺与误差曲面 例2 取三元函数 u(x1,x2,x3)= 边界取为a1=a2=a3=-0.1,b1=b2=b3=2.2,即区域Ω为[-0.1,2.2]×[-0.1,2.2]×[-0.1,2.2]。散乱点位于[0.9,1.2]×[0.9,1.2]×[0.9,1.2],由随机函数产生。分别用〈4,4,4〉阶,参数ρ=100的三奇次简单带自然边界条件的光顺样条与三奇次简单带自然边界条件的插值样条分别拟合函数u。在此仅列出当x3=1时,取500个散乱点(其中10个点上有值为1的噪声)和1 500个散乱点(其中15个点上有值为1的噪声)时光顺与插值的最大误差和平均误差(表2)。由表2可以看出,当测得的数据有噪声时,光顺的效果要比插值好很多,这说明光顺具有一定的去噪效果。 表2 x3=1时的误差 例3 取三元函数 相应的边界取为a1=a2=a3=-3,b1=b2=b3=3,即区域Ω为[-3,3]×[-3,3]×[-3,3]。散乱点位于[-2,2]×[-2,2]×[-2,2],由随机函数产生。用参数ρ=100为〈4,4,6〉阶三奇次简单带自然边界条件的光顺样条与〈4,4,6〉阶三奇次简单带自然边界条件的插值样条拟合函数u。在此仅列出当x3=1时,取1 500个散乱点的光顺曲面,插值曲面及曲面真实的等高线图(图3,图4,图5)。由等高线图可知,光顺曲面的等高线图更接近曲面真实等高线图。 图3 光顺曲面等高线 图4 插值曲面等高线 图5 曲面真实等高线 本文主要针对4维散乱数据,提出了一种带自然边界条件的样条光顺方法。在使得即定的目标泛函达到极小的要求下,给出了解的构造过程,得到了光顺问题的解——称为4维散乱数据带自然边界条件的光顺样条。这种光顺样条是三元的多项式,对每一个变量都奇次多项式,但并不要求关于每个变量的次数都是一样的,这使得在具体问题中对带自然边界条件的光顺样条可以根据需要选择其对每个变量的次数,如可选择带自然边界条件的光顺样条是〈4,4,2〉阶或者〈2,2,4〉阶的等等。从构造过程可知,这种三元带自然边界条件的光顺样条并不是由一元奇次多项式通过张量积的方法得到,是一种新的非张量积多元样条。由于是多项式,所以在计算上来说是较为简单的。但是由于篇幅的限制,本文只讨论和研究了这种带自然边界条件的光顺样条的特征与构造方法,而未能将如下的问题一一作出详细讨论: (i)光顺问题解的存在唯一性; (ii)光顺问题与插值问题的关系; (iii)光顺问题解的收敛性与误差估计; (iv)求光顺问题解时得到的线性方程组的特点及如何求解等。 对于以上问题将另文讨论和研究。 参考文献: [1]ANDREW R W.统计模式识别[M].王萍,杨培龙,罗颖昕,译.2版.北京:电子工业出版社,2004. [2]TONY F C,SHEN J H.图像处理与分析:变分、PDE、小波及随机方法[M].北京:科学出版社,2009. [3]唐泽圣.三维数据场可视化[M].北京:清华大学出版社,1999. [4]李岳生.分布欧拉方程与分片函数的表示[J].计算数学,2006,28(3): 225-236. [5]KAZHDAN M,BOLITHO M,HOPPE H.Poisson surface reconstruction[C]∥Proceeding of Eurogrouphics Synposium on Geometry Processing,Cagliari,Italy,2006: 61-70. [6]王仁宏.多元样条及其应用[M].北京:科学出版社,1992. [7]崔锦泰.多元样条理论用其应用[M].程正兴,译.西安:西安交通大学出版社,1991. [8]GUAN L T,LIU B.Surface design by natural splines over refined grid points[J].Journal of Computational and Applied Mathematics,2004,163(1): 107-115. [9]关履泰,罗笑南,黎罗罗.计算机辅助几何图形设计[M].北京:高等教育出版社∥海德尔堡:施普林格出版社,1999. [10]关履泰,覃廉,张健.用参数样条插值挖补方法进行大规模散乱数据曲面造型[J].计算机辅助设计与图形学学报,2006,18(3): 372-377. [11]LAI M J,SCHUMAKER L L.Spline functions over triangulations[M].London Cambridge University Press,2007. [12]LAI M J.Multivariate splines for data fitting and approximation,approximation theory[M].Brentwood: Nashboro Press,2008: 210-228 [13]ZHOU T H,HAN D F,LAI M J.Energy minimization method for scattered data hermit interpolation[J].Applied Numerical Mathematics,2008,58: 646-659. [14]吴宗敏.散乱数据拟合的模型、方法和理论[M].北京:科学出版社,2007. [15]李岳生,关履泰.散乱数据的二元多项式自然样条插值[J].计算数学,1990,23(1):135-146. [16]CHUI C K,GUAN L T.Multivariate polynomial natural spline for interpolation of scattered data and other applications[C]∥ Workship on Computational Geometry,World Sciedtific,1993:77-98. [17]关履泰.散乱数据的多项式自然样条光顺与广义插值[J].计算数学,1993,26(4): 383-401. [18]GUAN L T.A local basis for bivariate polynomial natural splines of scattered data[C]∥Guangzhou International Symposium of Computational Mathematics,1997. [19]GUAN L T.Bivariate polynomial natural spline interpolation algorithms with local basis for scattered data[J].J Comp Anal and Appl,2003,1:77 -101. [20]关履泰,许伟志,朱庆勇.一种双三次散乱多点项式自然样条插值[J].中山大学学报:自然科学版,2008,47(5): 1-4. [21]LAURENT P J.Approximation et optimization[M].Paris: Hermann,1972. [22]BEZHAEV A Y,VASILENKO V A.Variational theory of splines[M].New York: Kluwer Academic/Plenum Publishers,2001.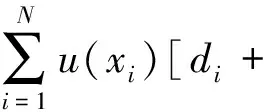
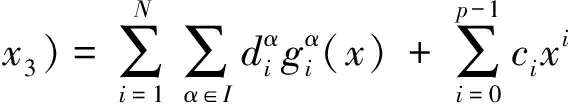
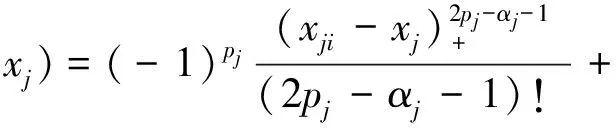
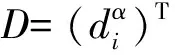
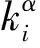
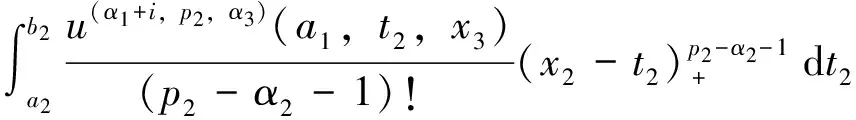
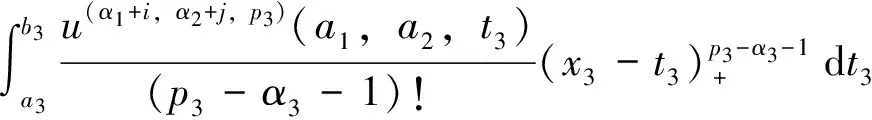
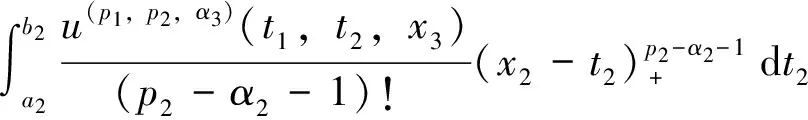
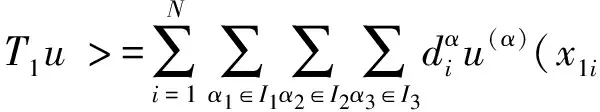
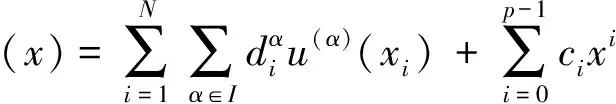
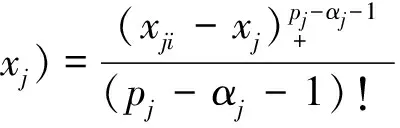
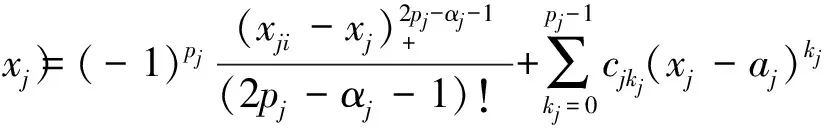
3 数值例子

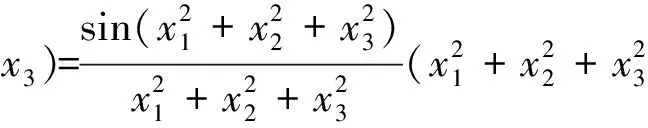
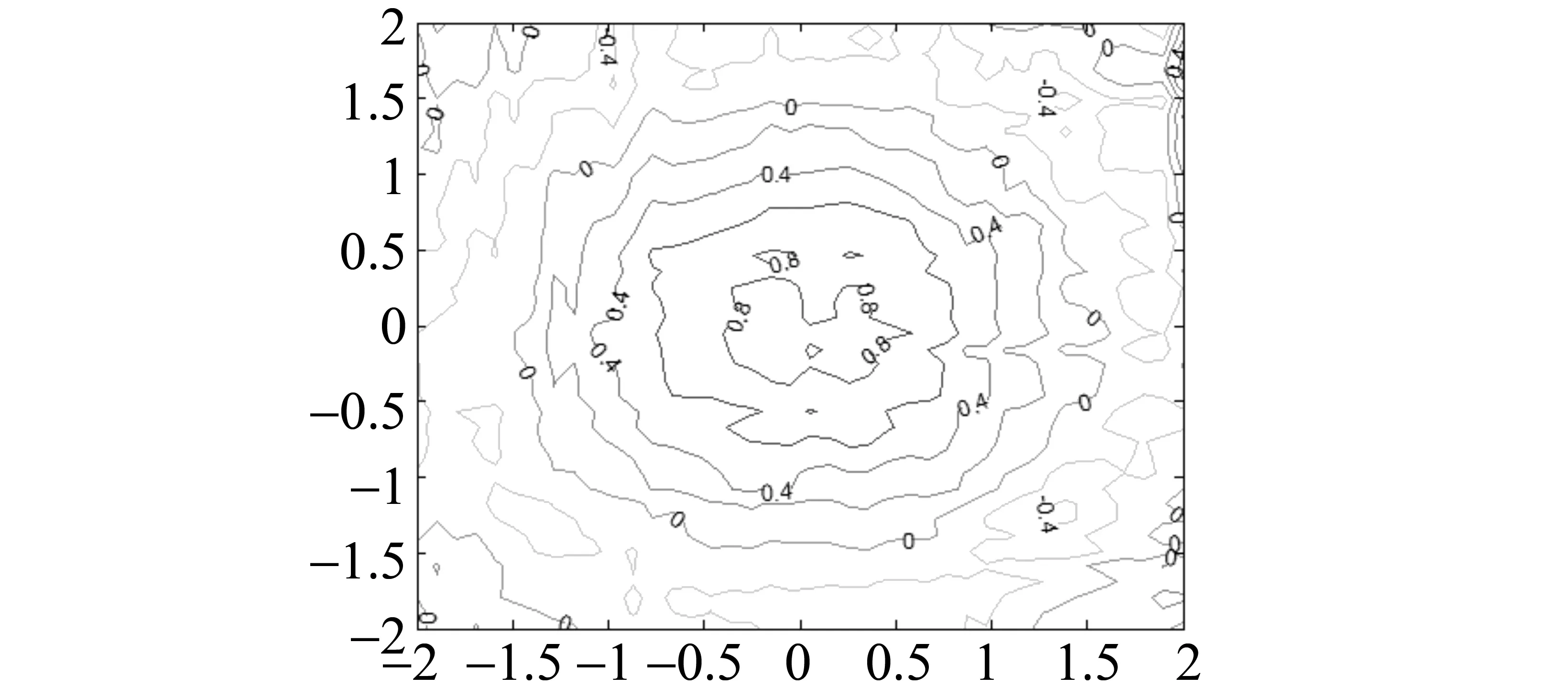
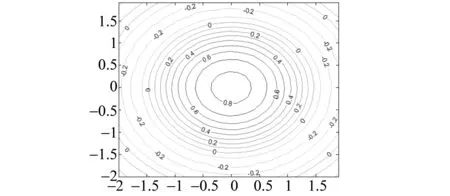
4 小 结

