图像隐写容量归一化研究

陈够喜，张鹏程，伍玉良

（中北大学 电子与计算机科学技术学院，山西 太原030051）

0 引 言

数字图像隐写的最大载荷是信息隐藏研究的热点之一，而信息隐藏的理论模型仍是Simmons提出的 “囚犯问题”模型［1］。在大量的空域图像隐写算法中，比较典型的隐写算法就是LSB替换算法，包括LSB替换隐写、MLSB替换隐写、±Κ及随机调制隐写等，而对于JPEG图像为载体的隐写技术中提出了典型的JSteg、OutGuess、F5和 MB等典型算法［2－3］，它们的本质均是将空域中的LSB隐写方法应用到量化后的DCT系数，提高载体的隐写容量。这些算法通过修改像素相应的LSB比特位，将隐秘信息嵌入到彩色或灰度图像之中。MLSB［4］替换隐写算法根据密钥选取图像的最低多个位平面上的比特位，然后将所选比特位用隐秘信息替换，又分为IMLSB和TMLSB。Sallee提出的基于模型的隐写框架［5］，通过修改不确定部分，既实现了隐秘信息的嵌入，同时又保持了它的分布不变，但不适合二值图像隐写。Tseng［6］提出了二值图像的经典算法。它允许在二值图像中的任何位置进行黑白像素修改，在一个的分块中，若允许至多改变其中的两个像素，则其最大的嵌入容量为但它只能适用于二值图像中。Wu［7］基于图像的连通性和平滑性的要求，依据二值图像分块的可修改度的分值提出的信息隐藏算法，隐藏容量和安全性与具体的图像有关，而且完全不适于灰度图像。

通过对灰度图像和二值图像的特征分析，本文基于图像LSB比特流的特点，提出了一种通用图像的大容量隐写算法，重点讨论和分析了至多修改1位的最大嵌入量，对灰度图像、彩色图像和二值图像进行了分类阐述，并通过实验验证了该结论的有效性。

1 改变像素中1位的容量分析

信息隐藏的主要载体是图像，通过对载体图像中的某些像素进行修改来实现携带隐秘信息。图像的隐写容量是指图像作为载体的最大有效载荷即载体图像中隐藏的比特数的总和。LSB（least significant bit）隐写算法是通过修改图像像素的最低有效位来实现信息隐藏，算法简单，能够实现大容量隐写［8］。

假设隐写目标载体图像为Q×W大小的灰度图像，记为Cg；隐秘信息记为S；采用B1和B0表示两位随机的二进制数列。Cg的像素值记为pi，其中0≤pi≤255，i≤Q×W，则像素值pi可记为

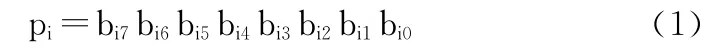
将S转换为二进制序列，记为S＝｛s1，s2，…，sn｝。隐秘信息S和转换的二进制序列是相互可逆的。通过计算D1＝bi2⊕bi1和D0＝bi2⊕bi0实现LSB的隐写［9］。下面先介绍定理1。

定理1 载体图像C中的任意一个像素pi的最低3位中，嵌入2位隐秘信息至多只需修改1位［9］。

证明：由于B1B0和D1D0均是两位2进制的组合，所以，可以归纳为分两种情形。

（1）当B1B0＝D1D0时，无需修改bi2bi1bi0中的任意一位即可嵌入2位隐秘信息B1B0。

（2）当B1B0≠D1D0时，分别为：

从前述假设和定义可得到

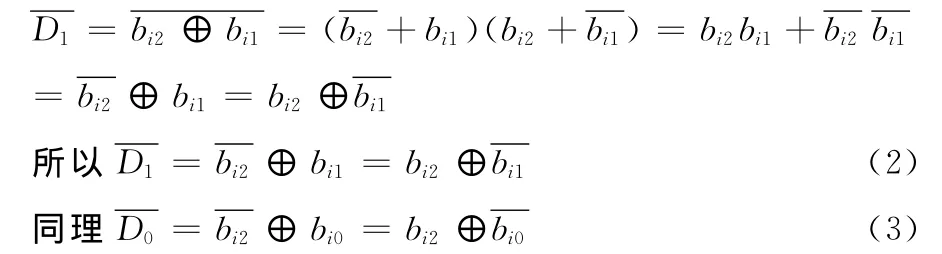
对比定义D1和D0以及各自的取反公式可得到（a）～（b）条件下可嵌入2位隐秘信息B1B0：（a）bi1取反；（b）bi0取反；（c）bi2取反。

可见，上述结论成立。

从上述定理1说明在灰度图像的LSB隐写中，最低3比特位中至多修改1位即可嵌入2位的隐秘信息。通常为了保持良好的视觉效果，实际隐写时，采用LSB的最低位平面中隐写，不仅嵌入效率高，又没引起视觉失真。若在最低的3个位平面中按照像素LSB嵌入隐秘信息，在特定的图像中，会引起较大的视觉失真。表1是嵌入前后的比特位变化的对比。

矩阵编码技术是由R.Crandal提出的，F5隐写由将它应用其中，大幅提高了隐写效率［10］。在一般意义上的LSB隐写中，平均修改LSB的一半才能嵌入1比特的信息，而矩阵编码的目的将实现以最低的修改率嵌入最多的隐秘信息。

表1 隐秘信息嵌入前后对比

下面给出矩阵编码的特殊形式［11］。即采用n个载体数据的LSB嵌入k个比特的隐秘信息，其中n＝2k－1。当最多只修改1比特时，记为（1，n，k），载体的嵌入效率为

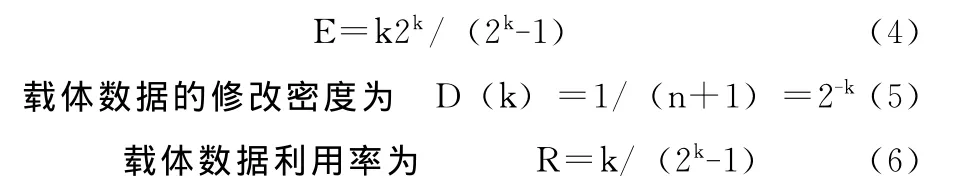
在F5隐写中，不同k值将直接影响载体的嵌入效率E和载体数据利用率R，从式（4）～（6）可以看出。表2列出了不同k值对应的矩阵编码的嵌入效率对比表。从表2的数据变化说明，当k＝1时，矩阵编码退化为基本的LSB隐写即定理1的表述。也可认为定理1是F5隐写的基本形式。当k值越大，载体嵌入效率E越大，相应的载体数据利用率就会越低。

将修改1位的数据嵌入推广到通用形式［11］。设载体数据LSB和隐秘数据的二进制形式分别表示为a＝a1a2…an，x＝x1x2…xn。定义散列函数载体可能由于嵌入隐秘信息发生数据位的修改，令y＝x⊕g（a），y为十进制数。

那么，将得到载体嵌入后的LSB序列

具体嵌入隐秘信息时，可根据表2选择最优的k值，使其得到最优的嵌入效率。

文献 ［12］通过分析和证明得到的结论：在一个m×n的二值图像块中，最多只修改1比特像素时的最大隐写容量为?log2（mn＋1） ，也可视为F5隐写在载体变为二值图像时的一种特殊形式。

表2 矩阵编码的嵌入效率对比［9］

表3是LSB隐写和定理1算法的性能对比。从表3中可以看出，采用定理1的改进算法，在数字灰度图像的最低位平面嵌入隐秘信息数据利用率最大为66.7%，而载体嵌入效率为33.3%，分别比LSB隐写的数据利用率降低33.3%，载体嵌入率33.4%

表3 定理1改进算法与LSB隐写算法的对比

从定理1和上面的分析可得到下面的推论。

推论1 对于Q×W的灰度图像Cg，至多修改像素中的1比特位时的最大隐写容量｜M｜＝2（Q×W）比特位。此定理的证明由定理1显然成立。

推论2 对于Q×W的彩色图像CC，至多修改像素中的1比特位时的最大隐写容量｜M｜＝6（Q×W）比特位。

彩色图像有RGB三分量，在每一个像素点分别有3个像素值分量，所以，隐写字节数就是灰度图像的3倍。

推论3 对于二值图像图像Cb的Q×W分块，至多修改像素中的1比特位时的最大隐写容量比特位［12－13］。

证明：在二值图像中，只有 “0”和 “1”两个像素值或状态。至多改变1位像素值时，图像分块就会有Q×W＋1种状态。而嵌入的最大容量｜M｜必然满足2｜M｜≤QW＋1即所以推论3成立。

上述推论3对于二值图像Cb的Q×W分块在最多修改1位时的最大隐写容量的上限进行了刻画，是文献 ［8］的重要结论，但若将其分块内的比特位进行有序排列，则它是本文定理1的特例之一。同理，对于二进制比特流也适用于本方法。

推论4 对于长度L的B＝b1b2…bj…bL二进制比特流，分块数为A，至多改变1比特位时的最大隐写容量为

证明：长度L的二进制比特流可以视为分块数为A的二值图像，分块的大小为？L/A？，依据推论3可得它的最大隐写比特数为

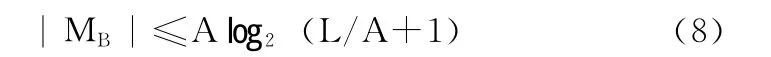
所以，结论成立。

推论4是推论3的一个推广，将二进制的比特流作为二值图像的一个分块考虑，从而得到至多修改1比特位时的最大隐写容量的上界。进一步可推广到可转化为二进制序列的任何载体图像的隐写容量的刻画，将彩色图像、灰度图像和二值图像有机结合在一起，得到关于任意图像至多修改一个像素中的1比特位时的最大隐写容量。

定理2 对于像素数量为N的任意载体图像C，图像的子块数长度为A，至多修改一个像素中的1比特位时的最大隐写容量其中α为图像类型值，对于二值图像、灰度图像和彩色图像，分别取1，2和3。

证明：将载体图像C转换二进制序列，其长度为N。应用推论3和4可知定理2的结论成立。

从定理2找到了灰度图像与二值图像的共同特征，即当把载体图像转换为二进制序列或比特流时，载体图像的外表特征将消失，内在特征将体现出来。对二进制序列进行隐写时，只要在每字节的LSB位进行修改，将不会影响载体图像的视觉效果或像素间的相关性。

由于二值图像只有 “0”和 “1”两个像素，导致大多数灰度或彩色图像的隐写算法不能推广到二值图像，反之亦然。但从数字图像的本质特征出发，发现灰度图像、彩色图像和二值图像的隐写容量在LSB下是一致的。为了提高的隐写容量，还可以对原始的二值图像进行分块，分块的大小也会对隐写的容量构成影响。灰度图像或彩色图像由于可能受到文件格式的影响，其对应的二进制比特流中的部分字节不能进行隐写，但真正的核心二进制序列均具有隐写特征的一致性，进而得到了任意载体图像至多修改一个像素中的1比特位的最大隐写容量的结论。因此，载体图像的LSB位隐写容量是由对应的比特流的长度决定，与载体的外部特征无关。

2 隐秘信息的嵌入与提取

在图像的LSB隐写中，它的嵌入和提取算法相对简单，算法复杂度低。

2.1 隐写位置确定

隐秘信息的隐藏位置通常由混沌映射和伪随机序列两种方法来确定，本文采用混沌映射。Logistic映射［14］表示为

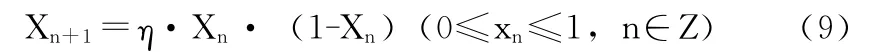
在上式中，当0.3569≤η≤4时，式（9）产生的序列是混沌序列。混沌序列在信号处理或传输时会表现为随机噪声和连续宽频谱等类似的特性［14］。当取特定的初始值X0和η，由式（7）经过迭代产生非周期和不收敛的序列，而且对初始值特别敏感。将载体的像素数量经过处理后映射到（0，1）之间，得到初始值X0，而且迭代次数必须大于20。

2.2 基于定理2的嵌入与提取算法

2.2.1 嵌入算法

（1）读取原始载体图像C，计算C中的像素的数量N和α，计算最大隐写比特数

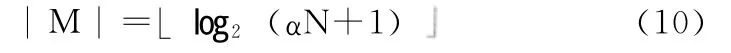
（2）隐秘图像S的预处理：包括隐秘图像S的置乱和转换为S′＝s′1s′2…s′i…s′n的二进制序列。S和S′的长度相同，设为，在密钥K的作用下，对S′进行加密，得到相同长度的序列S″＝s″1s″2…s″i…s″n。

（3）当l≤｜M｜时，进行隐写，否则退出。

（4）设定混沌映射的初始值η、X0和迭代次数，确定隐秘信息的嵌入位置。

（5）读取C的像素pi的最低3位，计算D1＝bi2⊕bi1和D0＝bi2⊕bi0，并将 D1D0和S″iS″i＋1进行对比，依据定理1进行修改相应的比特位，直至嵌入全部的隐秘信息。最后得到携密载体Cs。

2.2.2 提取算法

通过对定理1和2的分析，可知本算法为可逆算法，可准确提取出全部隐秘信息。

（1）读取携密载体Cs，计算C的像素数量N和α。

（2）依据混沌映射的初始值η、X0和迭代次数得到隐秘信息在Cs中的初始位置。

（3）依据定理1和2的规则，一次提取出S″＝s″1s″2…s″i…s″n。再在密钥K的作用下进行解密和再置乱，得到隐秘信息S。

2.3 基于推论3的嵌入与提取算法

2.3.1 密钥矩阵和权矩阵

在实现推论3的隐秘信息的嵌入时，需要引入密钥矩阵和权矩阵［6－7］。

设原始的二值图像F分拆为若干的m×n的分块Fi，隐写者和接收者同时拥有相同的密钥矩阵K和权矩阵W，而且K和W矩阵与分块的大小相同也是m×n，K内的元素是只包含0和1的随机矩阵。

隐藏信息的比特位数r≤log2（mn＋1），即隐秘信息为最大r位的比特流数据M＝b1b2…br，用（M）H表示 M对应的十进制数。权矩阵W定义为从SUM中至少取值一次。基于密钥矩阵K和权矩阵W的隐秘信息的嵌入算法如下：

（1）依据给定条件设定密钥矩阵K和权矩阵W。

（2）判断隐秘信息比特流的长度是否满足r≤log2（mn＋1），若不满足，则需替换原始二值图像载体。

（3）对于所有分块，计算Si，j，其中⊕表示矩阵异或操作，而表示矩阵按位乘，SUM表示的结果矩阵的全体元素之和。

（4）计算隐秘信息的嵌入位置集合

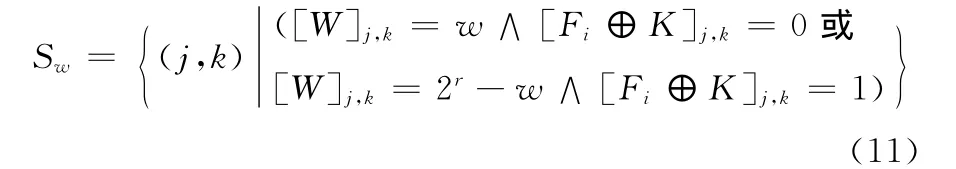
式中：Sw——修改原始二值图像的分块Fi后的SUM增加或减少w的所有满足条件的位置（j，k）的集合。

（5）对于非全白或非全黑的分块，计算权差

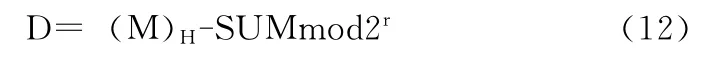
当d＝0，不进行任何嵌入操作；否则，任意选择一个h，h∈ ｛1，2，…2r－1｝，分别求出Shd和S－（h－1）d，并且满足Shd≠Φ和S－（h－1）d≠Φ，Φ 表示空集。在Shd和S－（h－1）d中各任意选择一个位置，替换 Fi中的对应位置上的值，Shd和 S－（h－1）d分别表示这一块中翻转后使SUM增加j×k和减少（j－1）×k的所有像素的位置的集合，从这2个集合中各自选择一个像素进行翻转，最终使SUM增加d。这些操作是保证S和（M）H与模2r同余。

2.3.2 嵌入算法

（1）把载体图像C转换为二进制序列，并等分为8H个子序列，H的取值越大越好。

（2）隐秘图像S的预处理同2.2.1，得到S″。

（3）将经过预处理的S″按照函数f分拆，得到子序列λ1，λ2，…，λj，…λn′，n′为分拆后的子序列的量。

（4）当l≤M时，进行隐写，否则退出。

（5）设定混沌映射的初始值η、X0和迭代次数，确定隐秘信息的嵌入位置。

（6）读取载体C的子序列的各像素pi的最低3位，计算D1＝bi2⊕bi1和D0＝bi2⊕bi0，并将D1D0和S″iS″i＋1进行对比，依据定理1进行修改相应的比特位，直至嵌入全部的隐秘信息。最后得到携密载体Cs。

提取算法同2.2.2，只是需要重新合并提取的隐秘信息的各子序列，才能得到完整的隐秘信息S。

3 隐写的安全性分析

基于数字图像的LSB隐写，隐藏容量较大，算法简单。通过定理1，可在最小修改度的情形下，得到最大的隐写容量。但它的安全性仍然可以保证。隐秘信息的预处理是采用置乱和加密，将隐秘信息转换为表面上无法分析的乱码。密钥K由密钥矩阵生成，矩阵的大小与载体图像相同设为Q×W。能够生成的密钥个数为

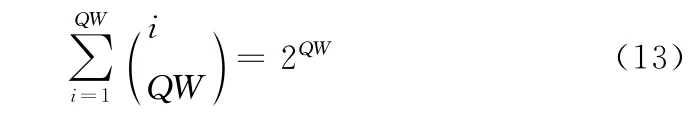
假设载体图像采用512×512的Lena.tif文件，那么生成密钥的总数为2262144，密钥破解难度极大。由式（8）产生的混沌序列具有的非周期和不收敛的特性，而且针对初始值非常敏感。将图像的像素个数经过函数X0＝f（N，｜M｜）生成，迭代次数大于20次（设为n＝50），生成X50。如果X50小于Q×W，那么X50即为隐藏的初始位置，否则，进行如下变换：X50＝?mod（X50）/（QW） 。

进一步分析，由于载体对应的二进制序列相对较长，只要等份的次数足够大，同时它也符合定理2的安全性定义的条件，那么隐写系统将是安全的。

4 实验结果与分析

下面以灰度图像和二值图像为例。灰度图像采用512×512的Lena.tif文件，隐秘信息采用文本文件text.txt，隐写方法采用定理1所阐述的LSB法，在像素的最低3位中，至多修改1比特位，计算其最大的隐写容量。根据定理1的推论1的公式｜M｜＝2（Q×W）计算，载体图像lena.tif的最大隐写容量的理论值为

它所携带的隐秘信息的安全性主要依赖于密钥的安全性。而采用定理2时，由于它是基于二进制序列的隐写，子块长度为A＝16，它的最大隐写容量为

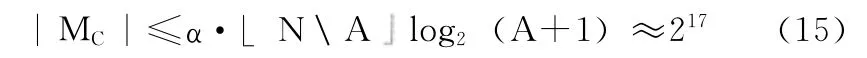
图1为隐写前后的图像，没有明显的视觉变化，但后者携带了大量的隐秘信息。基于定理1和2的隐写算法均是LSB隐写算法，表4是与文献 ［6］的对比分析，表5是与文献 ［15］基于安全性的对比分析。从上述分析中可以看出，定理1和2以及推论的有效性，隐秘信息量大，但抗攻击能力需进一步提高。

图1 灰度图像隐藏前后

表4 与TCP算法对比修改像素量对比

二值图像隐写的主要方法之一就是分块法。它对分块进行检测与变换，然后对满足条件的像素点进行翻转隐藏秘密信息。二值图像的隐写载体和携密载体如图2所示的文本载体。

图2 二值图像隐藏前后

为了适用定理1～2以及各推论，二值图像的分块采用1×A，符合二进制序列的特点，其中A＝64，则隐藏前的二值图像将由若干长度为64的子序列构成。子序列在至多修改1位时最大隐写容量为 ｜MC｜≤3×213，然而在实验嵌入式必须遵守下面规则：①全黑或全白的分块或子序列不能修改；②分块的嵌入能力的分析，相关性强的元素不能修改；③修改后可能变为全黑或全白的分块不能修改。结合上述3种情形，载体的分块数将大大减少。

Tseng在文献 ［6］中提出的TCP算法，在一个m×n的分块中，若允许至多改变两个像素，则其最大的嵌入容量为log2（mn＋1）。由于峰值信噪比（PSNR）和和均方差（MSE）主要是针对灰度和彩色图像的失真度进行度量的，因此，本文对二值图像的度量采用DRDM法［15－16］，它采用距离倒数的失真度表征图像的失真度，是刻画二值图像的失真度的一种方法。

表4是图2的载体分块和嵌入隐秘信息的数据分析，表5是与文献 ［6］TCP算法对图像质量对比的情形。表5反映了二值图像的图像失真度的变化情形，从实验的结果分析可看出本文算法不仅嵌入容量大，而且同比失真度较小，图像质量将更好。特别是在达到分块的隐写上限时图像的失真度的没有突出变化。由于本文的隐写算法修改像素少却能够达到文献 ［6］的嵌入效果，而失真度却没有明显变化，为设计大容量隐写提供设计方案。

表5 二值图像LSB隐写与TCP算法对比

5 结束语

数字彩色和灰度图像具有丰富的灰度层级，而二值图像只有 “0”和 “1”两个像素的变化，通用统一的数字图像的隐写容量通常难以实现。本文从数字图像的原始LSB隐写技术出发，分析了数字图像的LSB比特流及其相关变化情形，提出了并证明了基于LSB的各类隐写算法的归一化的结论，对彩色灰度图像和二值图像的最大隐写容量进行归一化，并将批量隐写最大容量增加了1倍。随着基于LSB隐写的局限性和隐写分析的进展，今后，将对大容量通用隐写容量及其安全性进行深入的研究和探讨。

［1］Cox I J，Miller L，Bloon A，et al.Digital watermarking and steganography ［M］.2nd ed.SanMateo，CA：Morgan Kaufmann，2008：1－13.

［2］LIU Fenlin，LIU Jiufen，LUO Xiangyang.Digital image steganalysis ［M］.Beijing：China Machine Press，2010（in Chinese）［刘粉林，刘九芬，罗向阳.数字图像隐写分析 ［M］.北京：机械工业出版社，2010.］

［3］ZHOU Qinglei，HUANG Minglei.Information hiding method for JPEG image ［J］.Computer Engineering and Design，2010，31（19）：4178－4181.）（in Chinese）［周清雷，黄明磊.JPEG图像的信息隐藏方法 ［J］.计算机工程与设计，2010，31（19）：4178－4181.］

［4］Nguyen B，Yoon S，LEE H.Multi bit plane image steganagraph ［G］.LNCS 4283：Proceeding of International Workshop on Digital Watermarking，2006：61－70.

［5］Sallee P.Moedl－based methods for steganography and steganalysis［J］.International Journal of Image Graphics，2005，5（1）：167－190.

［6］Tseng Y C，CHEN Y Y，Pan H K.A secure data hiding scheme for two－color images［J］.IEEE Transactions on Communications，2002，50（8）：1227－1231.

［7］WU M，LIU B.Data hiding in binary for authentication and annotation［J］.IEEE Transactions on Multimedia，2004，6（4）：528－538.

［8］Ker A D.Steganalysis of LSB matching in grayscale images［J］.IEEE Signal Processing Letters，2005，12（6）：441－444.

［9］CHEN Gouxi，CHEN Junjie.Research of capacity for batch steganography ［J］.Journal of Application Research of Computers，2011，28（9）：3492－3494（in Chinese）.［陈够喜，陈俊杰.批量隐写容量研究 ［J］.计算机应用研究，2011，28（9）：3492－3494.］

［10］SU Yajuan.One space field information hiding algorithm based on matrix encoding ［J］.Computer Engineering and Design，2009，30（23）：5344－5347.）（in Chinese）［苏亚娟.基于矩阵编码的空域信息隐藏算法 ［J］.计算机工程与设计，2009，30（23）：5344－5347.］

［11］Westfield A.F5－A steganographic algorithm：High capacity despite better steganalysis ［G］.LNCS 2137：Proceeding of 4th international workshop on information hiding.Berlin，Springer，2001：289－302.

［12］GUO Meng，ZHANG Hongbin，WEI Lei.Data hiding in binary images［J］.Acta Electronica Sinica，2009，37（11）：2409－2415（in Chinese）［郭萌，张鸿斌，魏磊.二值图像中的数据隐藏算法 ［J］.电子学报，2009，37（11）：2409－2415.］

［13］Yu Chiang Li，Chia Ming Yeh，Chin Chen Chang.Data hiding based on the similarity between neighboring pixels with reversibility［J］.Digital Signal Processing，2010，20（4）：1116－1128

［14］Collet P，Eckmann J P.Iterated maps on the interval as dynamical system ［M］.Boston：Birkhauser，1980.

［15］LU Haiping，Alex C Kot，SHI Yunq.Distance－reciprocal distortion measure for binary document image ［J］.IEEE Signal Processing Letters，2004，11（2）：228－231.

［16］Karsten M，Borgwardt A G，Malte J R，et al.Integrating structured biological data by kernel maximum mean discrepancy［J］.Bioinformatics，2006，22（14）：49－57.