图值神经网络体系结构及在蛋白质预测中的应用
张居晓 殷涛 孟朝晖
摘要:提出了一种新的蛋白质结构预测模型——图值神经网络。该模型以半边图理论为依据,用可结合半边图模型表示原子间和原子团间相互的结合作用,从而将对蛋白质的正确折叠起关键作用的大分子相互作用因素和环境融合进图值神经网络预测模型。此外,针对全原子计算量大的缺点,在图值神经网络中引入基团,从而在一定程度上减小了计算量。通过对模拟蛋白质折叠过程中能量变化的分析,实验表明这种融合了原子间以及原子团间作用力的模型是完全可行的。
关键词:蛋白质结构预测;图值神经网络;半边图;基团
中图分类号:TP393文献标识码:A文章编号:1009-3044(2012)01-0112-04
Architecture of Graph-valued Neural Network and its Application in the Protein Folding Prediction
ZHANG Ju-xiao1,YIN Tao2,MENG Zhao-hui2
(1.Nanjing Technical College of Special Education, Nanjing 210038, China; 2.Computer & Information College of Hohai University , Nanjing 210098, China)
Abstract: Graph-Valued Neural Network is based on the theory of half-link graph, it can not only be used to represent the force be? tween the atoms, but also the force between the atomic groups. Thus, the factors which play a key role in protein folding can be taken into Graph-Valued Neural Network. In addition, given the massive amount of calculation, we also bring“Group”into Graph-Valued Neural Network to reduce the amount of calculation to some extend. After analyzing changes of energy in the process of protein folding simula? tion, we come to a conclusion that the prediction model which combined with the force between the atoms and the force between the atomic groups is feasible.
Key words: Protein Structure Prediction; Graph-Valued Neural Network; Half-Link Graph; Group
仅依赖于蛋白质的一级结构(氨基酸序列)即可预测其二级甚至三级结构的传统观念。这一观念来源于诺奖得主Anfinsen[1]提出的蛋白质的一级结构决定其高级结构的学说。我们目前所见的大多数蛋白质结构预测的经典计算模型皆是建立在此学说的基础上。简单说,就是计算模型的输入数据仅仅为蛋白质的一级结构,经过模型的计算,输出为预测出的蛋白质的高级结构(二级结构和部分三级结构的关键部位构型)。但是分子生物学实验的研究成果早已表明,有许多蛋白质并不能自发折叠成正确的立体结构,需要在各种特定的细胞环境下并依靠其它生物大分子(包括蛋白质)的辅助才能形成正确的三级结构。在蛋白质结构预测的各种模型中,以(数值型)神经网络方法为主,这种模型虽然很成熟,但是不适合表达蛋白质中各原子相互作用,只能用来预测二级结构,并且二级结构的预测正确率也不高。在这时,α螺旋或β折叠二级结构只是被视为附加在一级结构上每个氨基酸的某种结构特征标记,并不考虑氨基酸链之间的相互作用关系及更复杂的立体相互作用,也就不能表示出蛋白质的三级结构。因此,目前尚缺乏一种合适的计算模型用于模拟考虑融合折叠环境的蛋白质三级结构的预测。
如果能够将蛋白质的真实折叠环境融合进预测计算模型,一定能够提高蛋白质结构预测的正确率,对蛋白质而言,其真实折叠环境就是异构酶、分子伴侣等因素。抽象而言,所谓蛋白质折叠的真实环境,实质就是大分子相互作用的环境。
综上所述,我们需要一种新的预测模型,该预测模型要设计得适于表现原子之间和原子团之间的相互结合作用,则该模型就能够模拟大分子相互作用的蛋白质真实折叠环境,并且该模型以不同层次、不同尺度的原子团为计算单元,则新模型也能够预测蛋白质的三级结构。
1图值神经网络模型
与神经网络模型类似,本文所提出的计算模型也具有输入、输出以及学习过程三种要素,但该模型与传统的神经网络却有很大的不同,即网络中传递的信息类型不同。原有的神经网络的输入、输出包括在其中传递的都是数值类型的信息,这种神经网络模型既无法考虑原子之间跟原子团之间的相互作用,也无法考虑异构酶、分子伴侣这些大分子对蛋白质的正确折叠所起的作用,而恰恰正好是这些作用,才是影响预测正确率的真正因素,因此,本文设计了一种图值信息,该信息能够较真实的模拟蛋白质的折叠环境,而传递这种信息的网络模型称之为图值神经网络。
除了网络中信息类型不同之外,两者神经元也有一定区别。一般的,神经网络其每层中的神经元个数在进行学习前都是已经确定好了的,但是图值神经网络中神经元是以原子为基础的,也即底层的神经元与蛋白质中的原子是一一对应的,考虑到每种蛋白质所包含的原子数目不同,因此,图值神经网络在数据输入前每层中的神经元个数是不确定的。
1.1输入预处理
对用作生物序列分析的神经网络而言,数据输入的预处理就是确定采用何种编码序列的方法把序列(字符串)转换成网络的输入向量,以便适合问题的解释。常用的编码方式为21位的二进制数表示的正交编码[2],其中20位用于表示20种氨基酸,每种氨基酸都对应了其中某一位为1其它位为0的情况。图值神经网络则跟传统的神经网络不同,其所需的输入将不再是数值型的,而是用半边图表示的图值。
1.1.1半边图模型
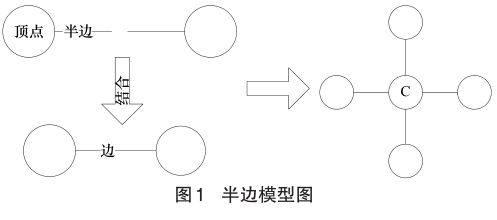
半边图模型[3]主要由三个要素组成:半边、顶点和边。半边是组成顶点的基本元素,一个半边属于某个顶点且分为不同的半边类型,半边与其它的半边可以相结合。顶点是组成图的基本元素,顶点本身由有序的若干个半边组成,具有n个半边的顶点,称为n度顶点。若两个顶点的两个半边的类型对是半边结合类型,则这两个半边就可以相结合,若两个半边已结合在一起,则两个半边合起来称为一个边。图1左半部分显示了两个一度顶点的半边结合过程。
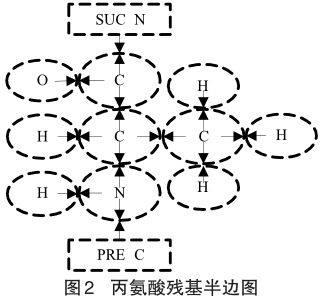
在实际的大分子结构中,不同的原子可以跟一个或多个原子相结合,用半边图模型表示这种关系就是n度顶点,如上图右半部分所示,中心顶点表示了一个碳原子,其四个半边分别与不同原子结合形成四条边。按照上述规则,将丙氨酸残基表示成的半边图如图2所示。
1.1.2基团、扭转角
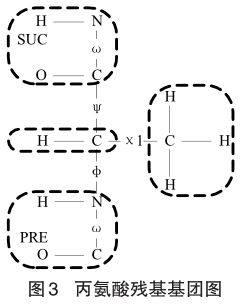
基团是由一系列原子构成的结构稳定的原子团。基团内部原子相对位置不变,而基团间原子相对位置是变化的。丙氨酸残基可以划分为4个基团,在图3中用虚线框表示,由于残基两端的基团由两个相邻残基中原子构成,这里分别用SUC、PRE表示后继、前驱残基部分。
扭转角由四个相邻原子构成,例如上图中的N-C-C-N构成扭转角ψ,C-C-N-C构成扭转角φ。扭转角按照其可以旋转的范围又分为广义扭转角和狭义扭转角。广义扭转角位于基团间,其取值范围较大,比如图3中的φ、ψ、χ1。有些广义扭转角如果排除受位阻限制以及位置重叠两种情况的话,可以自由旋转。狭义扭转角则位于基团中,取值范围较小,例如ω,其取值范围在180°范围内。
本文设想通过调整扭转角来模拟蛋白质的折叠过程,而有些原子团间的结构是稳定的,其形成的扭转角是固定的,我们将这些原子团划分为基团,这就是基团中的扭转角为狭义扭转角的原因。这样一来,模拟折叠只需调整广义扭转角,即基团间的扭转角。
1.2计算模型
计算模型中主要包括建立力场、扭转角、立体坐标、空间碰撞关系模型,而这些模型之间的关系如下:
1)扭转角、立体坐标:两者是互相确定的关系。
2)力场、立体坐标:吸力和斥力的计算依赖于立体坐标。
3)空间碰撞、立体坐标:空间碰撞的计算依赖于立体坐标。4)力场、扭转角:吸力或斥力推动扭转角的调整需求。
5)空间碰撞、扭转角:空间碰撞约束制约扭转角的调整。
其中,立体坐标是这些关系的纽带,但立体坐标不唯一,同样构型的蛋白质经过平移旋转后立体坐标就不一样,而扭转角能够唯一确定蛋白质的构型,这也是选择对扭转角进行调整的原因;空间碰撞模型根据立体位阻、空间重叠以及共价键旋转能障等建立;力场模型由电荷分布模型确定。
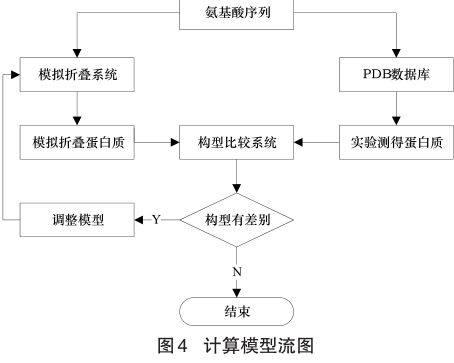
计算模型模拟蛋白质折叠的动态聚合过程,总体可以分为模拟折叠系统、构型比较系统、学习和修正系统三部分,三者间关系如图所示。
1.2.1模拟折叠系统
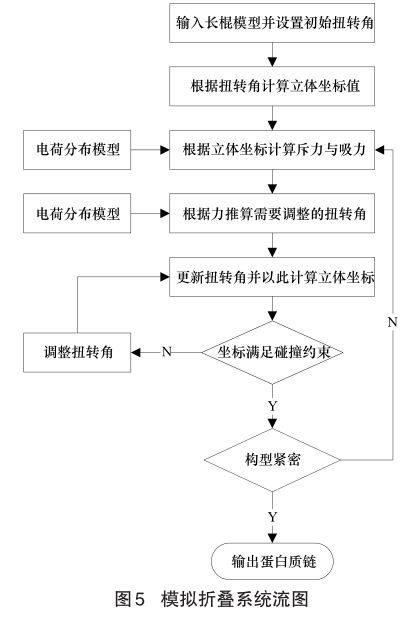
模拟折叠系统,将不含立体坐标信息的蛋白质序列折叠成具有合适空间结构的蛋白质。初始输入为一个长棍模型,所有的主链扭转角(φ、ψ、ω)为180°,其它的侧链扭转角(χ1、χ2、etc)从初始库中提取,然后按照吸力或斥力推动扭转角的调整,逐渐折叠为一个合适的立体构型,图5为模拟折叠计算流程。
1)根据长棍模型赋予扭转角初始值;
2)根据扭转角初值计算初始立体坐标;3)根据当前立体坐标计算吸力与斥力;
4)根据吸力与斥力推算出需要调整的扭转角并更新扭转角;
5)根据调整过的扭转角求出新的立体坐标;
6)判断新立体坐标是否满足碰撞模型约束,满足转8),不满足转7);7)根据碰撞模型约束微调扭转角,转5);
8)判断立体结构是否够紧密或者不用再调整,是就停止,否则继续转3)。
扭转角更新系统:是模拟折叠系统中的关键部分,该系统根据当前的吸力和斥力推算出需要调整的扭转角,并给出调整量。
对于小的、球型蛋白质,基本上是自发折叠的,而较大的蛋白质和膜蛋白质则需要其它蛋白质(折叠伴侣)和折叠环境的辅助。
每一个扭转角由其一定距离范围内的若干原子间吸力和斥力决定,反过来,每一对原子间吸力和斥力均推动一系列的扭转角的调整,扭转角和原子间力之间是多对多的关系,折叠伴侣和折叠环境的力关系也可以体现在其中,这里有很多种变化和选择,我们要尝试各种方案,这里是科研的重点。
1.2.2构型比较系统
构型比较系统,模拟折叠出的蛋白质与真实蛋白质(从PDB数据库中选取)会有不同,将模拟折叠出的构型与实际的构型进行比较,得出比较结果。这种比较是结构的比较,需要系统化的方法。
1.2.3学习与修正系统
神经网络方法在蛋白质二级结构预测中应用最广的是BP神经网络。这种网络模型使用的BP算法其主要思想是将学习过程分为3部分:
1)正向传播,该部分是输入信号从输入层经过隐含层传向输出层的过程;
2)反向传播,该部分是根据期望输出与实际输出的误差信号从输出层经隐含层向输入层逐层修正连接权值的过程;
3)正向传播和反向传播反复交替直至网络最终趋于收敛。
图值神经网络中的学习和修正系统可以借鉴BP算法中正向与反向传播这种思想,用构型比较的结果来调整模拟折叠的过程和参数,调整的目标有参数模型(比如电荷分布模型)和非参数模型(比如聚合方式模型,即吸引排斥方式模型)。
2实验与分析
这里选择1VII蛋白质[4]作为实验样本,首先,是因为该蛋白质有完整的从核磁共振实验获得的全部原子坐标数据,主要是包含所有的氢原子,其次,1VII的氨基酸残基数不太大,但却是一个相对完整的子域,能够做完整的力场分析。
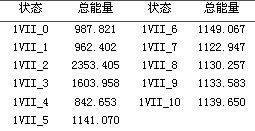
将1VII蛋白质从自然折叠状态(即从PDB数据库下载的1VII的原子坐标数据),逐渐解开成伸展状态(即最终主链上所有的扭转角φ为135°,ψ为225°),得到伸展状态的蛋白质结构,并且获取9个中间状态,加上初始的自然折叠状态共11个状态,对应得到11组立体结构数据,分别用1VII_0到1VII_10表示。
这里对于扭转角有三点需要注意的:
1)在生物化学领域,扭转角φ和ψ的取值范围为[-180,180],正方向为顺时针;而在我们的系统中,为了计算表示的方便,扭转角φ和ψ的取值范围定为[0,360],正方向为逆时针。所以在其它文献中,对应的伸展状态,扭转角φ为-135°,ψ为135°。
2)对伸展状态而言,也并非所有的扭转角φ均为135°,如果有脯氨酸的话,其扭转角φ受脯氨酸环形结构的制约,达不到135°,本实验中,21号脯氨酸残基的φ和ψ均不改变,所以,最终的伸展状态并不完全是一个长棍型,在脯氨酸的位置有弯折。
3)其它所有的扭转角φ和ψ按均等过渡的方法,计算出中间的9个状态,侧链的各个扭转角保持不变。
计算部分的总能量并非蛋白质结构中所有势能的总和,只是有变化的势能分量的总和,其它比如同一个基团中的各个原子之间也有势能,还有共价键能,等等,但是同一个基团中的各个原子之间的相对位置在折叠过程中没有变化或只有微小变化,这部分能量在折叠过程中没有实质性变化,而基团之间的位置关系在折叠过程中有显著变化,所以我们只考虑基团之间的总能量及其变化。
每个蛋白质结构都可以计算出其总能量,总能量为所有的两两基团之间的能量的总合。蛋白质1VII共有176个基团,则两两基团之间的能量值的数量为176*175/2 = 15400个,将这15400个能量值求和即为该蛋白质结构的总能量。
总能量的意义:这个值越小,表示蛋白质结构的总吸引力(负数)越大,总排斥力(正数)越小,可以比较的是,伸展状态1VII_10的总能量为1139,自然折叠状态1VII_0的总能量为987,这中间减小的差值152就是蛋白质折叠的目标。这个差值152是由15400个两两基团之间能量对的变化所贡献的。

图6基团总能量变化
折线图展示了从自然折叠状态在去折叠到达最伸展状态过程中,各种中间状态中能量的变化情况。除了1VII_2、1VII_3状态相较于其他状态明显偏大,其他状态基本呈现的是一个上升的趋势,也即该过程的逆过程(蛋白质折叠)中,各状态的能量是下降的趋势,这点符合蛋白质折叠过程的能量变化规律。从另一方面,也印证了本文引入基团这种思想是可行的。
注意,这里对于出现状态1VII_2这种情况需要说明一下,产生这种情况的原因是某些原子过于靠近导致的,当原子间距离过近时无法进行调整,使得计算出的斥力(正数)过大。解决该问题的方法是在模拟折叠系统中引入碰撞检测功能,当原子间出现像位置重叠这种情况时就可以对其进行一定调整。
3结束语
该文提出的图值神经网络是一个全新的概念,完全不同于先前的神经网络,是对蛋白质结构用全新方法进行预测的一次大胆尝试。其在继承神经网络方法优点的基础上,考虑了原子间的作用力因素,理论上必然可以提高蛋白质结构预测的正确率。目前,已经实现了图值神经网络的基本框架,并通过模拟蛋白质折叠过程对基团间能量变化进行初步分析,取得了比较理想的结果,证明这种引入基团并对扭转角进行调整的方案是完全可行的。虽然本次实验取得初步的成功,但整个体系还有待完善,比如在模拟折叠系统中加入碰撞检测机制,从而更加真实的模拟蛋白质折叠环境。
参考文献:
[1] Anfinsen C B. Principles that Govern the Folding of Protein Chains[J]. Science,1973,181: 223-230.
[2] Qian N,Sejnowski T J. Predicting the secondary structure of globular proteins using neural network models[J]. J Mol Bio,1988,202(4): 865-884.
[3]孟朝晖.半边图模型之多层次认知系统[J].计算机工程与应用,2006,42(30): 28-34.
[4] McKnight C J,Matsudaira P T,Kim P S. NMR structure of the 35-residue villin headpiece subdomain[J]. Nat Struct Biol,1997,4: 180-184.

