变频调速典型控制系统（五）

马小亮

（天津电气传动设计研究所，天津 300180）

第5讲 张力控制系统

冶金、造纸、纺织、化纤及电线（缆）加工等行业中的许多生产线都要求在加工过程中绷紧带材或线（缆），维持张力恒定，为此必须在生产线中安排一些专门控制张力的机械，它不担任加工材料任务，其转矩完全用来产生张力，例如卷取（开卷）机、张力S辊、活套、收（放）线 （缆）机等。由于张力由电动机转矩产生，所以这些机械的电动机控制系统的任务不是控制转速，而是控制张力转矩，转速取决于带（线）材移动的线速度v，是一个从属变量。称这类控制系统为张力控制系统，它实质上是转矩控制系统。

5.1 张力控制系统分类

5.1.1 按有无张力检测分类

按有无张力检测，张力控制系统分2类：直接张力控制系统和间接张力控制系统。直接张力控制系统需要张力传感器，通过张力闭环来控制转矩或转速。间接张力控制系统不需要张力传感器，而是根据张力给定值计算转矩给定，通过转矩环来控制张力。直接张力控制精度虽比间接张力控制高，但易出稳定问题，实际应用时不是简单的用张力调节器产生全部转矩或转速给定信号，而是以间接张力控制为基础，保留原转矩或转速给定计算，张力闭环只用来微调转矩或转速给定（微调范围5%～10%）。

5.1.2 按实现张力控制的途径分类

按实现张力控制的途径，张力控制系统分2类：通过转矩给定控制张力系统和通过转速给定控制张力系统。它们都基于由转速外环和转矩内环构成的双环基础调速系统。在建立张力后，前者的转速调节器ASR饱和，不参与控制，仅转矩环ATL工作，通过改变转矩给定来控制张力；后者的转速调节器ASR不饱和，ASR和ATL都工作，通过改变转速给定来控制张力。这两种控制系统的选择取决于张力负载的性质。如果微小的转速变化就能引起大的张力变化（刚性张力负载），则不适合用通过转速控制方法，因为没有转速调节的空间，容易引起振荡，转速才升高一点，张力就过大，转速刚降一点，张力又过小甚至消失，带材一松、一紧来回振，这时宜通过改变转矩给定来控制张力。如果微小转速变化引起的张力变化不大（弹性张力负载），有转速变化的空间，宜通过改变转速来控制张力，例如塑料薄膜（线）的生产线，随张力加大材料被拉长，又如某些带材加工线中的张力S辊，随张力加大带材下垂量减小，它们都有转速调节空间，这时通过改变转矩给定来控制张力反而可能引起弹性振荡，参见本讲第5.5节。

间接张力控制系统没有张力调节器，大多采用通过转矩给定控制张力系统，但在遇到弹性张力负载引起弹性振荡时，需引入转速增量信号来抑制振荡（见5.5节）。直接张力控制系统有2种可能的控制方法：对于刚性张力负载，宜用通过转矩给定控制张力系统，这时张力调节器输出是转矩给定微调信号（附加转矩给定ΔT＊）；对于弹性张力负载，宜用通过转速给定控制张力系统，这时张力调节器输出是转速给定微调信号（附加转速给定Δn＊）。

5.1.3 按有无卷径变化分类

卷取机和开卷机示意图绘于图1，卷取机把生产加工出来的带（线）材卷在套筒上，随生产进行，收集的材料不断增加，卷径D逐渐增大；开卷机把成卷的原料送出去加工，随生产进行，原料不断送出，卷径D逐渐减小，它们的卷径D都是变化量。生产工艺要求在加工过程中带（线）材的张力和线速度v不变，这样卷取和开卷电动机的转矩和转速就要随D变化而变化，为此控制系统必须先检测和计算D，然后根据它来计算转矩和转速给定值。另外随D变化，电动机负载的转动惯量也在变，相应加减速所需的动态转矩补偿量和转速PI调节器的比例系数也要随之变化。卷径变化使得控制系统复杂。

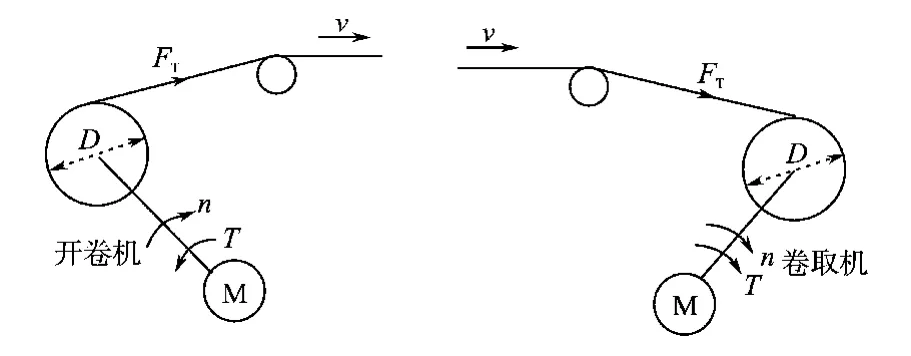
图1 卷取机和开卷机示意图

张力S辊示意图绘于图2，它只产生张力，不收集或发送带（线）材，无卷径变化问题，不用计算卷径，直接根据张力给定和线速度来设定转矩和转速给定值，相应动态转矩补偿量和转速PI调节器的比例系数也是固定值，控制系统简化了许多。

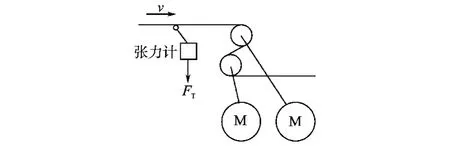
图2 张力S辊示意

5.2 通过转矩给定控制张力系统的单动、联动和断带（线）保护

开始生产前，先要上料和穿带（线），这时张力控制机械处于单动工作状态，与主机无机械联系，调速系统应是有转速外环和转矩内环的双环转速控制系统，通过点动和爬行来完成上述任务。开始生产时，转入联动工作状态，张力机械通过爬行把带（线）材绷紧，在张力机械和主机间逐步建立起张力，然后带张力随主机加速至工作速度，这时调速系统应是只有转矩环的张力控制系统，转速调节器退出控制。生产结束前，张力机械和主机带张力一同降速至停止，这时仍是联动工作状态，调速系统仍只有转矩环。生产结束后，要卸料，张力机械又改回单动，调速系统改回双环转速控制系统。上述工艺过程要求调速系统能方便地在转速控制和张力控制系统之间从一种平滑过渡到另一种。

在生产过程中如果发生断带（线），张力突然消失，由于这时转速环不工作，张力控制系统的转矩环继续维持电动机转矩不变，张力转矩变成加减速的动态转矩，造成卷取机和张力S辊突然加速，直至飞车，开卷机突然停车并反向转起来，非常危险，迫切需要断带（线）保护。

能满足上述2项要求的通过转矩给定控制张力调速系统框图示于图3，它是由转矩内环ATL和转速外环ASR构成的双环系统，其特点是张力控制的转矩给定信号不是直接送至ATL输入，而是从转速调节器ASR正限幅输入。

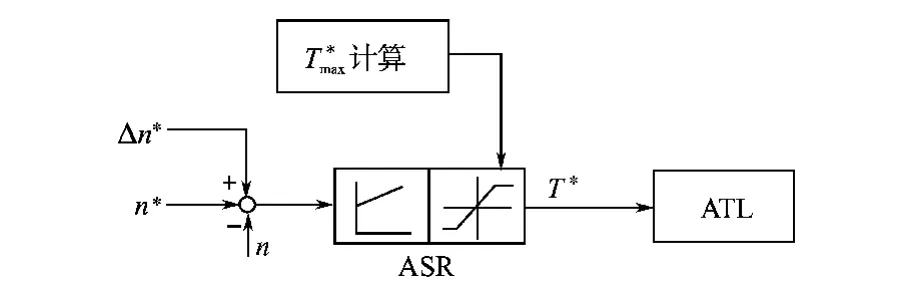
图3 通过转矩给定控制张力调速系统框图

在单动时，附加转速给定Δn＊＝0，ASR限幅值为固定值，这时的调速系统是标准的双环转速控制系统，转速环和转矩环都工作，由于张力尚未建立，张力机械与主机无机械联系，所以张力机械的转速等于其给定值，完成上、卸料及穿带任务。穿带完成后，发出联动指令，施加附加转速给定Δn＊＝5%～10%到ASR输入，卷取电动机低速爬行，慢慢绷紧带（线）材。在带（线）材绷紧后，受张力牵制电动机爬不动，转速n＜n＊＋Δn＊，ASR正向饱和并退出控制，这时ATL的转矩给定输入T＊等于ASR的正限幅值，从而实现从转速控制到张力控制的平滑过渡，张力大小通过改变来控制（ASR的负限幅仍为固定值）。在联动期间，主转速给定n＊按满足带（线）材以线速度v移动所需的电动机转速来设定，因此在整个生产过程（加速、稳速及减速）中都是n＊－n≈0，靠Δn＊维持ASR正饱和，调速系统按张力控制模式工作。

如果在工作中发生断带（线）故障，卷取或张力S辊电动机加速，在转速升高5%～10%后，n＊＋Δn＊－n＝0，ASR退出饱和并恢复控制，调速系统自动转回转速控制模式，转矩给定T＊减小，转速被限制在n＝n＊＋Δn＊。监测ASR是否饱和的信号还可用作发出“断带”联锁信号的依据之一，如果在联动期间，张力已建立（张力大于门槛值），发现ASR退出饱和且能维持一定时间便可判断为“断带”。这个延时时间很重要，否则会因转速信号抖动而误发“断带”信号。

开卷机工作情况略有不同，规定它的正方向为张力转矩方向（T＞0）和开卷时电动机旋转方向相反（n＜0，见图1），因此转速给定为－n＊，而附加转速给定Δn＊仍为＋，张力控制时ASR正饱和，是正限幅值，通过它来控制张力大小，电动机工作在再生状态。断带（线）后，张力转矩变成减速转矩，电动机减速，当转速减到n＝－n＊＋Δn＊时ASR退出正饱和，调速系统转回转速控制模式，转速被限制在n＝－n＊＋Δn＊。

5.3 卷取和开卷机的间接张力控制系统

5.3.1 卷取和开卷变频器主电路

卷取和开卷电动机功率小于1MW，所以它们的变频器宜采用交－直－交电压型PWM 变频器。

从图1知：卷取工作时，电动机转速和转矩方向一致，工作于电动状态，功率流动方向是从中间直流母线经逆变器流到卷取电动机；开卷工作时，电动机转速和转矩方向相反，工作于再生状态，功率流动方向是从开卷电动机经逆变器流向中间直流母线。根据这个特点，变频器主电路最好采用公共直流母线方案，把开卷机和卷取机（或／和主机）的逆变器接在同一段直流母线上，示于图4。这样安排后，开卷机发出的再生功率通过直流母线直接转流到卷取机或／和主机（开卷、卷取和主机同时工作），不再流到制动单元和电阻，从而大大减小整流器、制动单元和电阻的容量。通常在计算整流器、制动单元和电阻容量时都不计入开卷功率，因为开卷工作后流过这3个设备的总功率都将减少，不会增加。

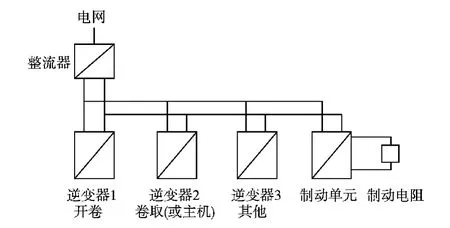
图4 变频器主电路

5.3.2 开卷和卷取电动机负载特性及容量选择

本小节讨论开卷和卷取电动机的负载特性（转矩、功率与转速关系）及容量选择，讨论基于2个前提条件：

1）忽略电动机及机械的空载转矩，因为它小于5%；

2）不计加减速的动态转矩，开卷和卷取电动机加减速较平稳，动态转矩不大，可以利用电动机和变频器的过载能力来满足它，故在选择电动机容量时不考虑它。

开卷和卷取电动机的转矩、转速和功率公式如下

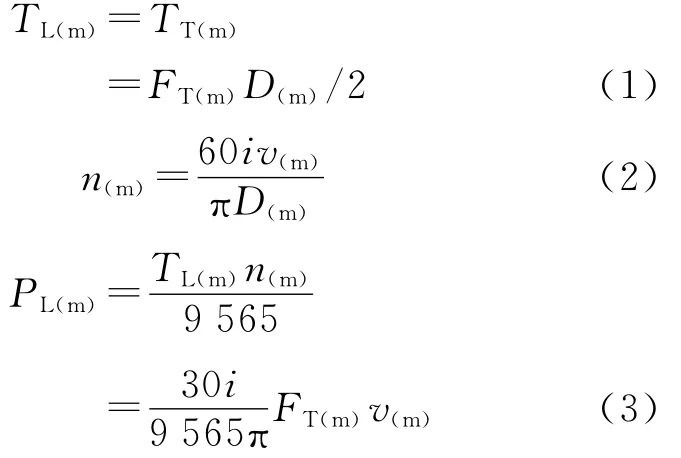
式中：所有变量的下标（m）表示这变量是有量纲和单位的测量值，无此下标表示该变量是无量纲和单位的相对值（数字控制器中的量）；TL（m）和TT（m）分别为电动机负载转矩和张力转矩，N·m；FT（m）为张力，N；D（m）为卷径，m；v（m）为带（线）材线速度，m／s；n（m）为电动机转速，r／min；PL（m）为电动机的负载功率，kW；i为减速机速比。

由式（1）～式（3）知：在张力FT（m）和线速度v（m）不变条件下，转矩TL（m）与卷径D（m）成正比，随D（m）增大而加大；转速n（m）与卷径D（m）成反比，随D（m）增大而降低；功率PL（m）与卷径D（m）无关，也就是说在卷径变化期间负载功率不变。

在张力最大（FT＝FT.max）且不变条件下，转矩、功率与转速的关系示于图5。以开卷过程为例说明负载转矩TL和功率PL变化情况：在建立张力时线速度v≈0，相应n≈0，这时由于卷径最大（D＝Dmax），故负载转矩也最大（TL＝TL.max），位于A点，负载功率PL＝0（因为n≈0）；升速期间，随v从零增加到vmax，n从零增加到nB，假定在这期间D没变，则TL维持最大值不变，工作点从A过渡到B，PL从零线性增长到PL.max：恒速生产期间，v＝vmax不变，随D减小，n继续增加，TL沿反比曲线减小，当D减至最小D0时，n增至最大nmax，工作点从B过渡到C，这期间PL维持PL.max不变；在减速期间，假定D＝D0不变，则工作点从C过渡到D。卷取过程的工作点移动轨迹与开卷相反，从D点出发，经C和B，到达A。

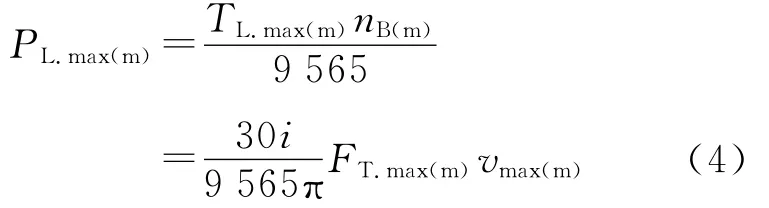
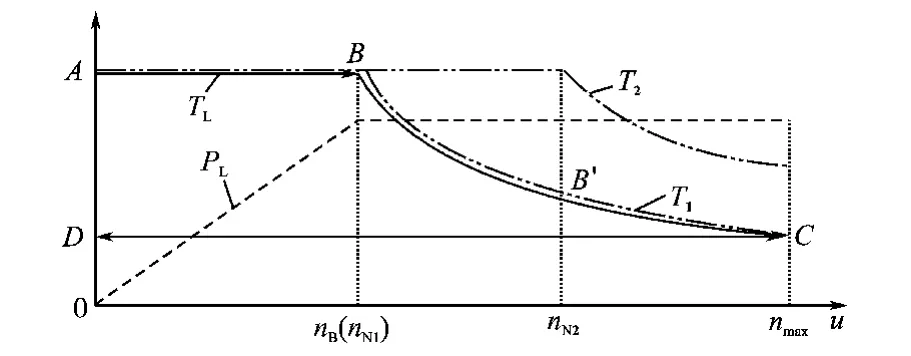
图5 转矩、功率与转速的关系

负载特性与调速系统的恒转矩调速和恒功率调速特性形状一样。若选择电动机的额定转速nN.1＝nB，则只要电动机额定功率

就能满足生产要求，电动机的调速特性为图5中的曲线T1。在开卷到B点时，电动机电压已升至额定电压，基础调速系统中用电压控制的自动弱磁控制环节开始工作，随后转入恒功率调速区，电压不变，磁链减弱，同样转矩电流产生的转矩与转速成反比，所以电动机的负载转矩电流在整个开卷（卷取）过程中都维持不变（不包括加减速动态电流）。

这种选择电动机容量的方法有时不能实现。按此法电动机的恒功率调速范围nmax／nN.1应等于卷径变化范围Dmax／D0。开卷（卷取）电动机的功率等级小于1MW，适合采用异步电动机，由于在恒功率调速段异步电动机的颠覆转矩随n升高按平方关系减小（见第1讲1.2节），所以它的恒功率调速范围受限制，一般≤2，而卷径变化范围常达3～4或更大。以卷径变化范围＝3为例，如果要求恒功率调速范围nmax／nN＝3及电动机在nN时颠覆转矩＝2.5TN（TN为电动机额定转矩），则在nmax时，颠覆转矩 ＝2.5TN／32＝2.5TN／9＝0.28TN，这时负载转矩TL＝TL.max／3，电动机将拖不动负载。解决该问题的办法是，在保持电动机额定转矩不变条件下，提高其额定转速至nN.2，令nmax／nN.2≤2，相应电动机额定功率也增大nN.2／nB倍，即

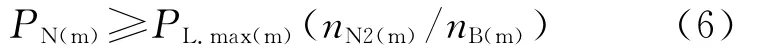
电动机的调速特性为图5中的曲线T2。由于电动机的体积和重量取决于转矩，而不是功率，所以按此法增大功率后，电动机体积和重量不变，但变频器功率加大。采用该电动机后，在开卷过程的A－B段，电动机负载转矩电流维持最大不变；在B－B′段，由于仍在电动机的恒转矩调速区，随D减小和n升高，电压升高，负载转矩电流减小，负载功率不变；在B′点，n和电压都升至额定值，自动弱磁控制环节开始工作；在B′－C段，恒功率调速，电压和功率不变，负载转矩电流维持减小后的值不变。

为避免在卷径变化范围大时增大电动机容量，某些大型开卷和卷取机改用励磁同步电动机传动，因为在高性能变频调速系统中，励磁同步电动机都工作在功率因数＝1状况下，在恒功率调速段最大转矩与（n／nN）成反比，不存在与（n／nN）2成反比情况。

5.3.3 开卷和卷取电动机的间接张力控制

开卷和卷取电动机的间接张力控制采用图3所示的通过转矩给定控制张力系统，它的恒功率调速用基础调速系统中的自动弱磁控制环节实现，余下的问题是如何根据期望的张力和线速度v＊来计算图3中的转速给定n＊和ASR的正限幅给定。

5.3.3.1 卷径D计算

由于n＊和都与卷径D有关，故先算卷径。由式（2）知：

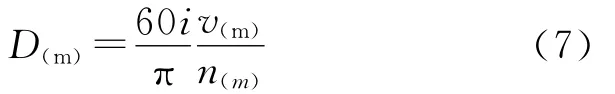
在数字控制系统中，所有变量都是相对值，须把式（7）改写为相对值表达式：

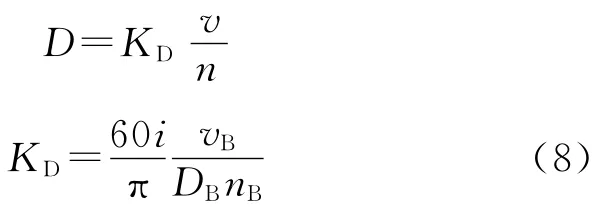
式中：vB为线速度基值，m／s，通常选用最大线速度vmax为基值；DB为卷径基值，m，通常选用设备允许的最大卷径Dmax为基值；nB为转速基值，通常选用电动机额定转速nN为基值；KD为比例系数，在选定上述各变量基值及减速比i后它是常数。

直接按式（8）计算D存在3个问题：

1）v和n信号的波动及噪声导致D波动；

2）断带（线）时，该计算公式不成立；

3）断带（线）后需停机（控制电源不停）处理事故，若原来算的卷径数据丢失，在处理完事故后恢复再生产时，卷径数据不对。

有多种解决上述问题的方法，最常用的是数字电动电位器法。数字电动电位器实质上是积分器，输入＋1信号后，输出按一定斜率上升；输入－1信号后，输出按一定斜率下降；输入0时，输出不变；停机时输出保持原数据不丢失。基于数字电动电位器的卷径D计算框图示于图6，图6中DPM是数字电动电位器，CMP是比较器，Dini是初始卷径信号，S是卷取／开卷工作模式选择开关，v是线速度实际值信号，来自测速辊或主机，n是卷取／开卷电动机转速实际值信号。

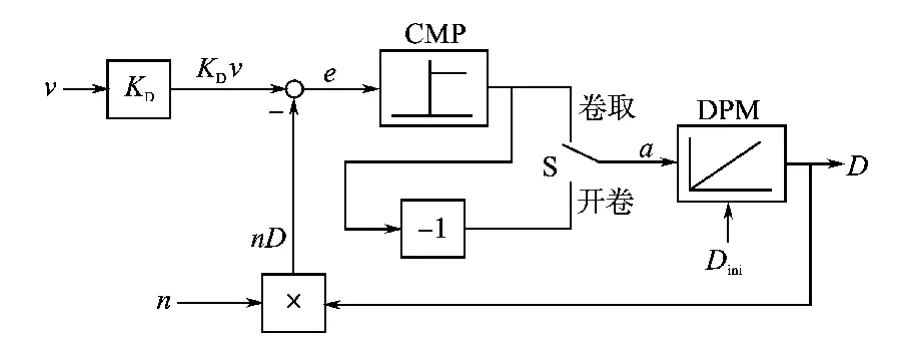
图6 D计算框图

以卷取过程为例说明计算过程。开始工作前先置选择开关S于卷取位置，并设置Dini＝D0（空套筒直径）。开始卷取后，随实际卷径增大，n降低，e＝KDv－nD＞0，CMP输出＋1，DMP输入a＝＋1，DPM输出的卷径信号D从D0开始加大，直至e≤0，a＝0，DPM输出停止变化，到再次发现e＞0时，D再加大，如此反复使D跟随实际卷径逐渐加大，一直保持D≈KDv／n关系。DPM输出变化速度不要设置得太快，只略大于实际卷径的变化速度，这样在信号v和n波动时，D来不及变化，即使变大了一点，它也不会退回来，而是等到实际卷径超过该值后再开始跟随，从而防止了由v和n波动带来的D波动。发生断带（线）后，卷取电动机转速n迅速上升，e＜0，a＝0，D维持断带发生时的值不变。在停机（控制电源不停）处理断带（线）事故期间，由于a＝0，DPM仍保持断带发生时的D值不丢失，待到再开机生产时，D计算从该值的基础上开始。

开卷时，先置选择开关S于开卷位置，并设置Dini等于来料原始卷径。开始开卷后，随实际卷径减小，转速升高，由于此时v和n都是负值，仍然e＝KDv－nD＞0，CMP输出＋1，经反号器a＝－1，DPM输出的卷径信号D从Dini开始减小，直至e≤0，a＝0，DPM输出停止变化，也实现D≈KDv／n。由于开卷时a的输出状态只有0和－1，所以在整个开卷过程中D只逐步减小，不后退。发生断带（线）后，卷取电动机转速迅速下降，e＜0，a＝0，D维持断带发生时的值不变。

5.3.3.2 转速给定n＊计算

为在整个卷取／开卷过程中使ASR处于饱和状态，n＊应该等于在有张力牵制条件下的电动机实际转速n，由式（8）得：

式中：系数KD的定义见式（8）。

5.3.3.3 正限幅给定计算

由控制框图（图3）知，在建立张力后就是转矩环ATL的给定T＊，即

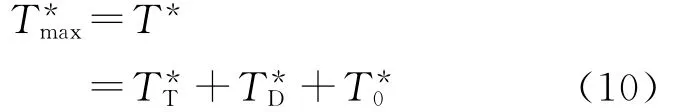
式中：为张力转矩给定；为加减速动态转矩给定；为电动机和机械空载转矩给定。

上述转矩给定都是相对值，它们的基值TB是电动机额定转矩TN，即

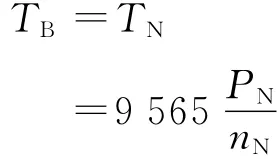
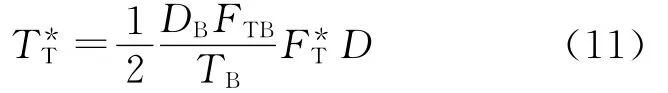
式中：DB为卷径基值，m；D为卷径相对值；FTB为张力基值，N；为张力给定相对值，＝／FTB，为张力给定测量值，N。

电动机的动态转矩给定为

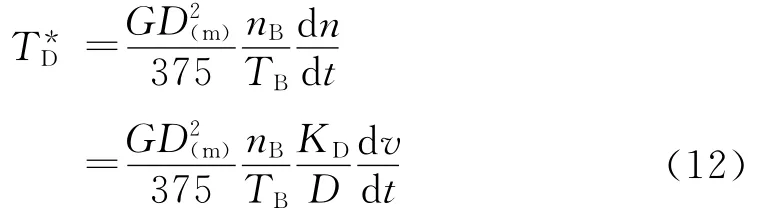
由式（1），电动机的张力转矩给定为

（由于卷径D变化很慢，在推导此公式时认为dD／dt＝0）

式（12）中：为电动机、机械和卷材总的飞轮转矩

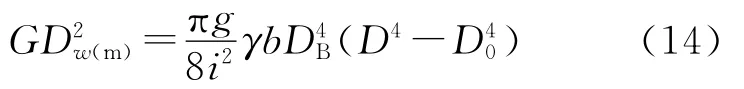
式中：g为重力加速度，m／s2；r为卷材比重，kg／m3；b为卷材宽度，m；i为减速机速比。

电动机和机械空载转矩很小（＜5%），常忽略，但若张力变化倍数大，空载转矩与最小张力转矩相比不可忽略时，就必须设置。它近似是转速n的二次方函数，在实际系统中常通过空转电动机和机械测取空载转矩曲线T0＝f（n），然后用函数发生器来分段近似。

5.3.3.4 转速调节器中比例系数自适应

控制框图（图3）中的转速调节器ASR在建立张力后处于饱和状态，它的PI调节功能不工作，但在上卷、卸卷及断带时，ASR退出饱和，调速系统返回转速控制模式，它的PI调节功能恢复工作。从文献［1－2］介绍的调节器参数工程计算方法知，ASR中的比例系数VRn与电动机、机械及卷材的总飞轮转矩GD2成正比。卷径D变化时，GD2随之变化，相应VRn也需做出适当调整来适应它的变化。VRn自适应框图示于图7，其中FG是存有GD2＝f（D）曲线的函数发生器（在D＝D0时f（D）＝1），VRn.0是D＝D0（无卷材）时的VRn，VRn＝f（D）VRn.0。

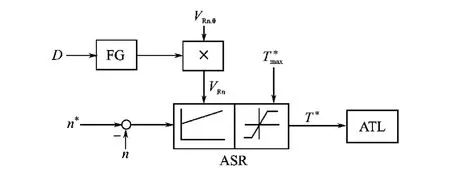
图7 VR.n自适应框图

由于总GD2中，电动机和机械的（无卷材）占有较大份额，在D／D0≤3时总GD2变化不大，不必使用VR.n自适应环节。

5.4 直接张力控制系统

5.4.1 卷取和开卷机的直接张力控制系统

对于张力控制来说，间接张力控制系统是开环控制，按照张力和线速度期望值算出转矩给定，通过转矩环ATL去控制转矩，实际张力是多少不知道，故它的张力控制精度受限制。要想进一步提高张力控制精度，就要装设张力传感器，加入张力调节器，改用直接张力控制系统。与间接张力控制系统相比，直接张力控制系统的卷径变化倍数与张力变化倍数之乘积可以从40提高到100，线速度可以从600m／min提高到2 000m／min。直接张力控制易出现稳定问题，因为在张力降到零（松带）后张力闭环断开，控制结构的突变易导致振荡。以卷取为例，松带后张力反馈消失，卷取机加速，带材突然绷紧，张力反馈超过给定值，卷取机减速，带材又松开，如此反复造成振荡。为解决这问题张力闭环按微调设计，调节范围≤10%。

依照卷取（开卷）机与主机联系的紧密程度不同，直接张力控制系统又分2类：在微小转速变化能引起大张力变化（刚性张力负载）场合，采用通过转矩给定控制张力系统；在微小转速变化只引起微小张力变化（弹性张力负载）场合，采用通过转速给定控制张力系统。为防止振荡，张力调节器不能在开始工作之初就投入，需先用间接张力控制建立稳定张力，然后再投入该调节器，甚至延时到带张力加减速完成之后的稳速段才投入。在加工结束松带前，也需要先撤除张力调节器。

5.4.1.1 通过转矩给定控制张力的直接张力控制系统

通过转矩给定控制张力的直接张力控制系统用于刚性张力负载，框图示于图8。它基于通过转矩给定控制张力的间接张力控制系统，转矩给定经ASR的限幅施加到ATL输入，图8中，D，n＊，，和的计算与间接张力控制一样，但张力转矩给定为

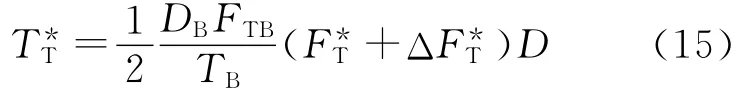
式中，Δ是张力给定微调信号，来自张力调节器AFTR的输出，它被限幅在10%左右。AFTR的输入是张力给定和来自张力传感器的张力反馈信号FT。

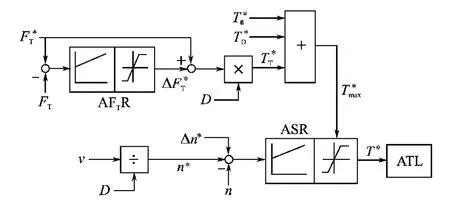
图8 通过转矩给定控制张力的卷取（开卷）机直接张力控制系统框图

接收到建立张力信号后，施加附加转速给定Δn＊，待ASR饱合后，转入张力控制。为防止张力振荡，在建立张力过程中要先闭锁AFTR，另外在解除张力控制前也要闭锁AFTR。如果卷径变化倍数＞3，ASR也需要PI调节比例系数VR.n自适应环节，实现方法与图7相同。

5.4.1.2 通过转速给定控制张力的直接张力控制系统

通过转速给定控制张力的直接张力控制系统用于卷取（开卷）材料是易拉伸的弹性材料（例如塑料箔材）场合（弹性张力负载），它们为通过转速控制张力提供了转速变化空间。这种控制系统的框图示于图9。

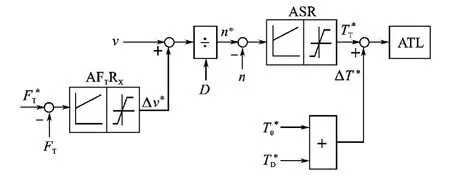
图9 通过转速给定控制张力的卷取（开卷）机直接张力控制系统框图

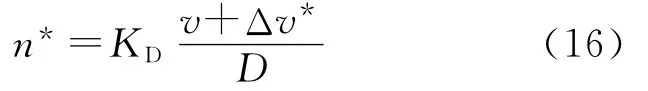
式中，v为线速度信号，Δv＊为线速度微调信号，来自张力调节器AFTR的输出，它被限幅在2%～10%。AFTR的输入是张力给定和来自张力传感器的张力实际值FT之差。对于卷取机，若FT＜，Δv＊加大，使n＊加快，绷紧带（线）材，减小张力误差；对于开卷机，若FT＜，Δv＊加大，由于v是负值，n＊减慢，也绷紧带（线）材，减小张力误差。

AFTR的投入和解除过程与通过转矩给定控制张力的直接张力控制系统相同。如果卷径变化倍数＞3，ASR也需要PI调节比例系数VR.n自适应环节。

5.4.2 张力S辊的直接张力控制系统

S辊是带材生产线中常用设备，用来控制带材在某生产段的速度。它由2或3个辊组成，每个辊由1台电动机驱动，带材包在这几个辊外，以扩大带材和辊面接触的面积，增加摩擦，从而增加对带材的拉力。S辊传动采用主从控制，按主辊的工作模式，它分2类：速度基准S辊和张力S辊。速度基准S辊的任务是控制该生产段带材移动的线速度v，它的主系统采用无转速静差的双

该系统转矩环ATL的转矩给定由3部分组成：张力转矩给定、动态转矩给定和空载转矩给定。和的计算与间接张力控制相同，来自转速调节器ASR的输出。ASR的转速给定为环基础调速系统，任务是使v等于其给定值。如果生产段很长，一组S辊拉不动全段的带材，就需要增设第2或第3组S辊。一个生产段中有几组S辊后，就出现S辊间转速协调和负荷分配问题，所以新增设S辊的主系统都采用张力控制，它们的任务是使带材张力FT等于其给定值，转速n则取决于v，系从属变量，称这类S辊为张力S辊，见图2。由于存在“打滑”可能（“打滑”时主从辊间机械联系断开），S辊的从系统宜采用通过转速环实现负荷均衡系统SLBS，参见第4讲4.3节（有机械联系的多电动机主从控制系统）。

张力S辊大多采用直接张力控制。与卷取（开卷）机的直接张力控制系统一样，按实现张力控制的途径，张力S辊的直接张力控制也分2类：通过转矩给定控制张力系统和通过转速给定控制张力系统。它们的工作原理也和卷取（开卷）同类系统相同。与卷取（开卷）机不同，张力S辊不存在卷径变化问题，D＝D0＝常数，不需要D计算，相应n＊，和的计算都被简化，ASR的VR.n自适应环节取消，由于张力变化倍数小，补偿也被取消。

通过转矩给定控制张力的S辊直接张力控制系统示于图10。

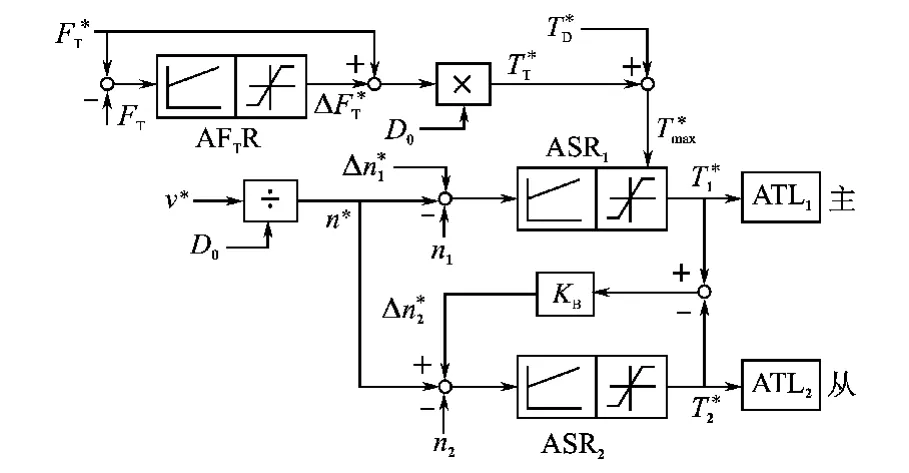
图10 通过转矩给定控制张力的S辊直接张力控制系统

由于张力S辊用于长的生产段，在两组S辊之间的带材会有一定下垂量，转速微小变化引起下垂量变化，有一定转速变化空间，即使用于不易拉伸材料的张力S辊也常采用通过转速给定控制张力的S辊直接张力控制系统，见图11。

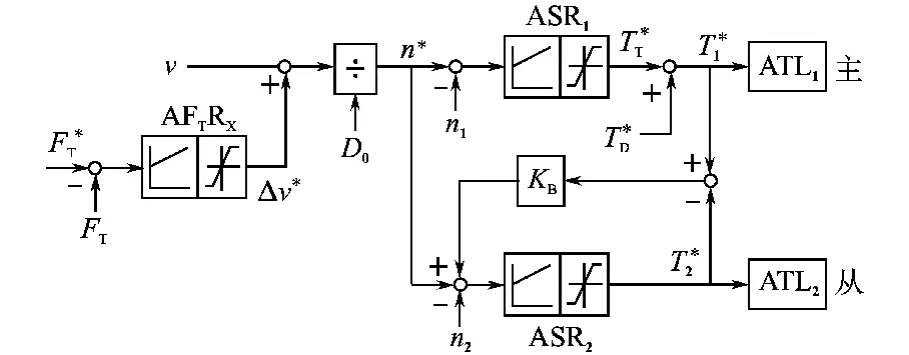
图11 通过转速给定控制张力的S辊直接张力控制系统

为防止张力振荡，AFTR输出被限幅于10%或更小。另外在建立张力过程中和解除张力控制前，也要先闭锁AFTR。

5.5 通过转矩给定控制张力系统的弹性振荡及抑制［1，3］

从前面介绍知道：对于刚性张力负载，通过转速给定控制张力系统易振荡；对于弹性张力负载，则通过转矩给定控制张力系统易振荡，即使采用间接张力控制也一样。通过转矩给定控制张力的间接张力控制系统，转速调节器饱和，根据线速度和张力期望值计算转矩给定，通过转矩环ATL使实际转矩等于给定值。这时，转速开环，没有张力调节器张力也是开环，粗想起来这系统不应有稳定问题，但是如果负载张力有弹性（张力大小与拉伸量成比例），人们可以看到一个奇怪的振荡现象，电动机转矩平稳不变，而转速和张力却在来回振荡。本节分析产生这种弹性振荡的原因，并介绍抑制方法。

下面以卷取系统为例说明弹性振荡的起因。卷取机示意图见图1。在讨论稳定问题时认为线速度v和卷径D不变（信号v来自主机，不受张力波动影响）。

振荡发生时，张力FT＝FT0＋ΔFT，张力转矩TT＝TT0＋ΔTT，电动机转矩T＝T0＋ΔT，转速n＝n0＋Δn，转角

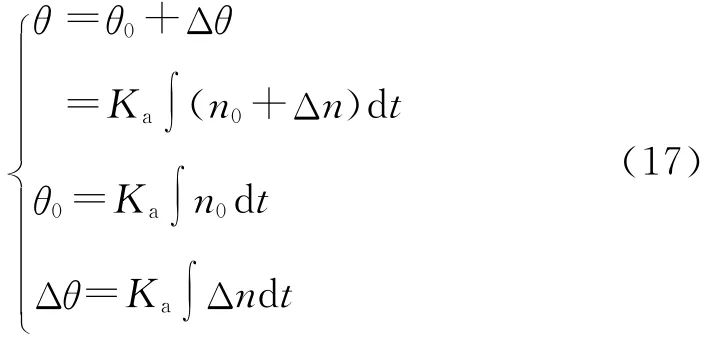
（上述几个表达式中变量下标0表示无振荡时的值，Δ表示振荡带来的增量）

电动机运动方程

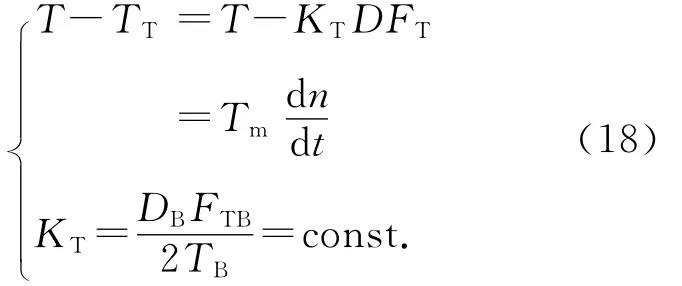
把上式中各变量改写为无振荡值＋增量形式。无振荡时

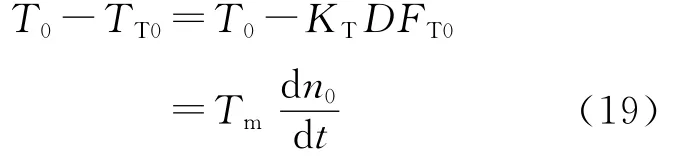
比较式（18）和式（19）

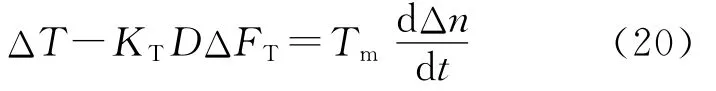
间接张力控制的转矩环ATL使T＝T＊＝T0，不受张力转矩和转速振荡影响，ΔT＝0。

对于弹性张力负载

把式（11）～式（17）和式（21）代入式（11）～式（20），得运动方程

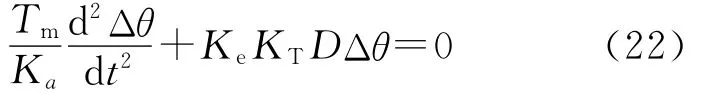
这是二阶不衰减振荡方程。弹性系数Ke越小，振荡频率越低，振幅越大。对于刚性张力负载，Ke非常大，振荡频率很高，电动机和机械响应不了，振荡不会发生。

抑制弹性张力振荡的方法是在转矩中引入转速增量信号，令

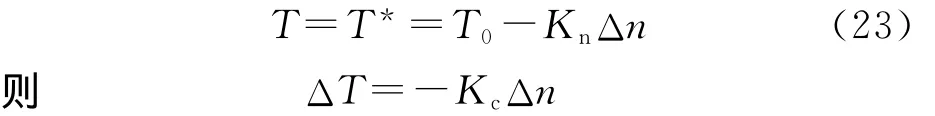
代入式（20），得运动方程

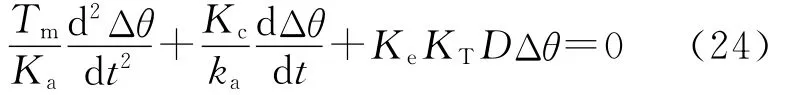
这是二阶衰减振荡方程，弹性张力振荡被抑制。

实现上述抑制方法的框图绘于图12。图12中转速给定n＊按式（5）～式（9）算出，它近似等于n0，n＊－n≈－Δn。与间接张力控制系统框图3相比，本图ATL的输入信号T＊（转矩给定信号）中增加了－KcΔn分量。不振荡时，Δn≈0，－KcΔn分量不影响张力控制，它只抑制振荡。

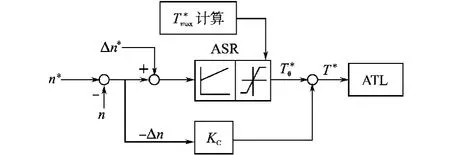
图12 抑制弹性张力振荡框图

实例1：某铝板冷轧机，它的来料较厚、硬，在第1道轧制的卷取过程中，板材产生很大抗弯曲弹力，电动机拉紧一点，板材就弯过来，卷紧一点，电动机放松一点，板材又弹回去，卷又松开，电动机负载转矩的大部分都被用来克服这弹性。开始采用图3所示系统，出现明显振荡，电动机电流和转矩稳定不变，而转速一快一慢，铝卷一紧一松来回振。在后几道轧制时，铝板薄了，抗弯曲弹力没了，系统工作正常。后改用图12所示系统，在转矩中增加－KcΔn成分，上述振荡问题解决。

实例2：某带钢加工线的水平活套示于图13，电动机驱动绞车，通过钢绳拉动活套车水平移动，绷紧钢带。活套的任务是贮存一定数量的钢带物料，维持生产线生产的连续性，v1和v2分别是钢带输入线速度和输出线速度，在冲、放套时v1≠v2，这时电动机转速n比例于v1和v2之差，正常工作时v1＝v2，电动机堵转n＝0，在整个生产过程中都维持张力转矩不变。活套电动机的任务是产生固定的张力转矩，它不需要动态转矩和空载转矩补偿，也无断带可能，从原理上说其控制系统只需要转矩环（不需转速外环）和固定的转矩给定T＊，起初人们确实设计了一个这样的系统，但工作起来后发现弹性振荡，虽然电动机实际转矩等于给定值不变，很稳定，无波动，而电动机却来回转动，带材一松一紧抖动。

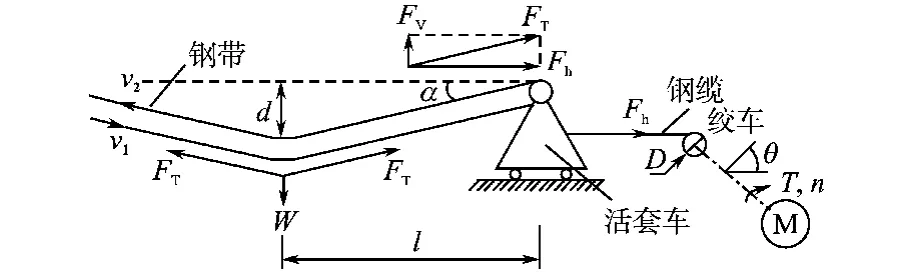
图13 带钢水平活套

钢带的重量W由带钢张力FT平衡，将FT分解为一个垂直分量Fv和一个水平分量Fh，Fv＝W／2，Fh＝Fvl／d（d是钢带下垂量，l是从下垂最低点到活套车的水平距离）。钢缆的拉力（张力）等于Fh，电机以转速n旋转，转角θ加大，活套车右移，l加大，d减小，Fh加大。Fh和转角θ间是非线性关系，在分析稳定时都采用小信号增量，经小信号线性化后FT和θ间的关系可以用下式近似表示

式（25）表明，水平活套车传动也是一个弹性张力负载，虽然调速系统只有一个张力环（简化的间接张力控制系统），也存在稳定问题。

解决这问题的办法也是在转矩中引入－KcΔn成分，框图示于图14。图14中n0是无振荡时的电动机转速，即

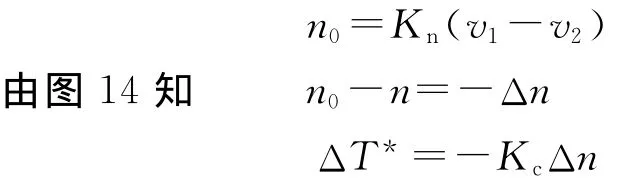
采用此措施后，振荡消除，钢带拉紧。

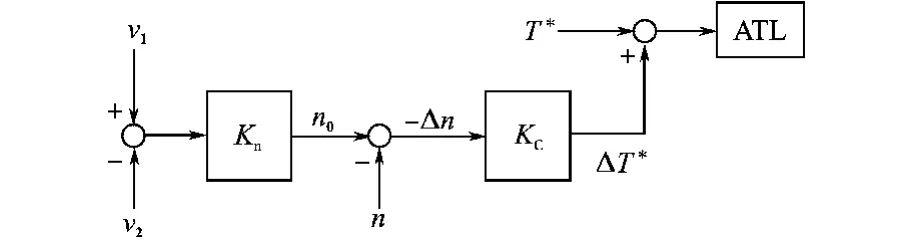
图14 水平活套控制框图

［1］ 马小亮.高性能变频调速及其典型控制系统［M］.北京：机械工业出版社，2010.

［2］ 陈伯时.电力拖动自动控制系统［M］.第3版.北京：机械工业出版社，2003.

［3］ 马小亮.驱动弹性负载的调速传动［J］.电气传动，2008，38（7）：3－7.

（未完待续）