手持GPS测量面积变形误差研究＊

路 琪，景 欣，勾志阳，钱 旭，晏 磊

（1.中国矿业大学（北京）机电与信息工程学院，北京100083；2.北京大学空间信息集成与3S应用北京市重点实验室，北京100087）

0 引 言

GPS采用空间距离后方交会的方法确定待测点的位置。并已广泛应用于测绘、军事、交通、邮电、地矿、煤矿、石油、建筑、气象、公安、农业、林业等部门和行业［1］。手持GPS具有简单、便携的特点，在测量面积方面也有很多应用［2－4］。手持GPS测量面积是采用向量积方法计算面积，这就需要先将WGS－84坐标转换为高斯平面直角坐标，然后以平面直 角 坐 标 求 解 面 积［5－7，8－10］。 由 于 高 斯 平 面直角坐标选择直角坐标系中央子午线离所测地区距离越远，误差就会越大。手持GPS的面积计算功能并没有考虑这些误差。以GARMIN vista型GPS为例，探讨面积测定的方法，并对其精度进行评价，分析误差出现的原因，为此类GPS提供参考。

1 原理与方法

1.1 向量积求面积原理

对于不自交的多边形，可以利用向量积的方法求面积。向量积也被称为叉积，叉积的长度｜a×b｜可以解释成以a和b为边的平行四边形的面积。a×b的方向满足右手法则，顺时针方向为负方向，逆时针方向为正方向，所以计算面积需要取绝对值［5］。

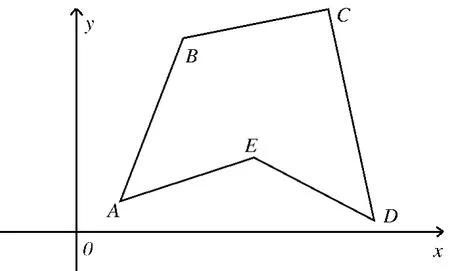
图1 向量积求多边形面积

如图1所示，在多边形ABCDE所在平面任取一点，为方便取原点O，则多边形ABCDE的面积

1.2 高斯平面直角坐标

由于地球面是不可展曲面，若简单地将曲面拉平，必然产生裂口和褶皱。采用投影的方法来确定地球面与平面上点位之间一一对应的关系，就能解决地球面不能直接展开的矛盾。但这必然会产生投影变形［11］。

设想一个平面卷成横圆柱套在地球外，如图2所示。通过高斯投影，将中央子午线的投影作为纵坐标轴，用x表示，将赤道的投影作横坐标轴，用y表示，两轴的交点作为坐标原点，由此构成的平面直角坐标系称为高斯平面直角坐标系。每一个投影带都有一个独立的高斯平面直角坐标系［11］。

图2 高斯投影

高斯投影是正形投影，没有角度变形，在中央子午线上也没有长度变形，但不在中央子午线上的各长度比均大于1，且距离中央子午线越远，变形越大。

设地球上两点A（x1，y1）、B（x2，y2），A与B的中点C（xm，ym），设大地线长为s，两投影点间的直线长度为d，地球平均半径为Rm，Δy＝y2－y1.如图3所示，则有高斯投影距离改化公式

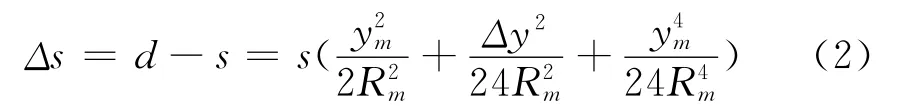
图3 高斯投影距离改化

WGS－84与北京54坐标系是一种椭球参数的转换。作为这种转换在同一个椭球里的转换都是严密的，而在不同的椭球之间的转换是不严密的［12］。

1.3 测定方法

利用GPS测定面积

1）测定各航路点的经纬度，转换为高斯平面直角坐标后再利用向量积法计算面积。

2）进入GPS的航线画面，将通过环绕所测场地边界航路点组成航线，用GPS的“航线面积”功能来求得面积。

3）用GPS所测面积与计算面积比较，确定手持GPS测定面积的精度范围［1－2］。

2 测量仪器与实验方法

2.1 测量仪器

GARMIN vista型GPS，其主要性能为定位频率每1s一次；误差5～25m以内；内置GPS天线，标准RS－232接口。可以存储1 000航路点、20条航线。

2.2 实验方法

GPS需要同时能够接收到4颗卫星信号。为了测量数据的稳定性，选择比较开阔的场地进行实验。这里选择了未名湖湖心岛进行实验。绕行湖心岛一周，在拐点记录下航路点坐标，并使用MAPSOURCE软件将数据从手持GPS中导入计算机。航路点组成的航线可以直接在手持GPS中测量航线所围区域的面积。

3 结果与分析

3.1 实验结果

1）使用GPS分别测量10个航路点、记录坐标值，构成一个闭合导线；这10个航路点需要在同样条件下多次测量取平均值。2）使用手持GPS自带“航线面积”功能计算测量结果坐标组成区域的面积。3）向量积法计算面积。将测量结果坐标转换为直角坐标后代入式（1）中，计算面积。

测量坐标结果如表1所示。

手持GPS自带“航线面积”功能计算的结果为4 351.669m2.

用公式（1）计算面积需要将WGS－84坐标转换为高斯平面直角坐标。实验所测地区中央子午线为E117°，计算面积为4 342.12m2.与手持GPS自带“航线面积”功能计算的结果相比，相对误差为0.22%.

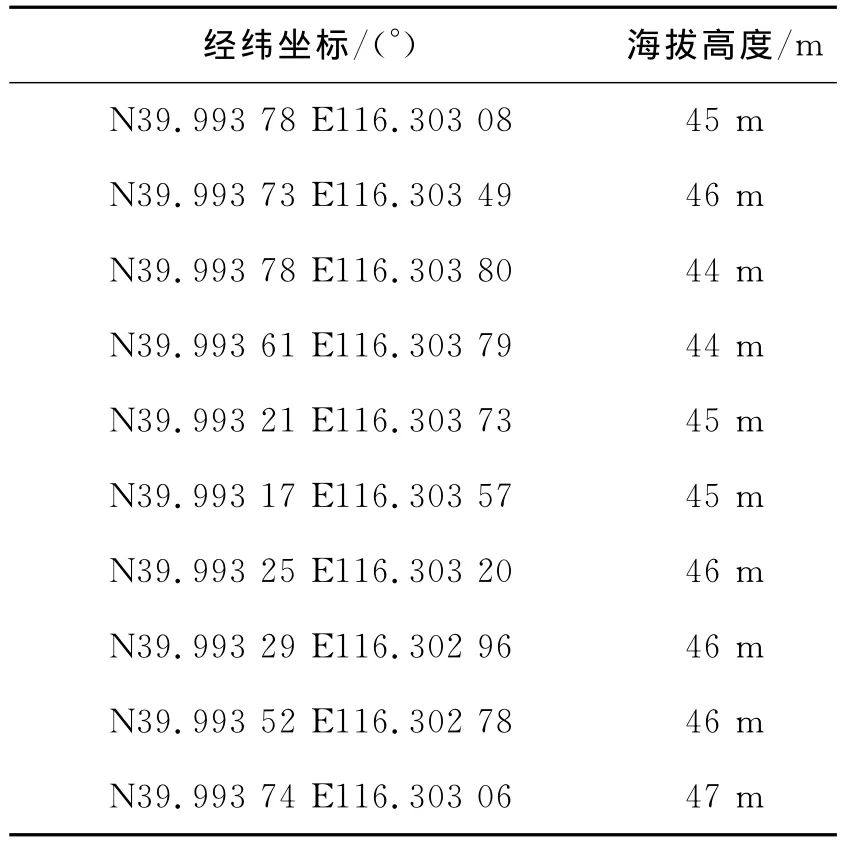
表1 GPS所测各航路点坐标（未名湖湖心岛）

3.2 实验分析

由于高斯平面直角坐标选择直角坐标系中央子午线离所测地区距离越远，误差就会越大。使用向量积方法求面积只需要相对坐标即可，选取的经线越靠近这10个点越精确而需要刻板地选择中央子午线，选为经过湖心岛中心附近的116.303 2°是最接近的。选取经线与计算的面积如图4所示。

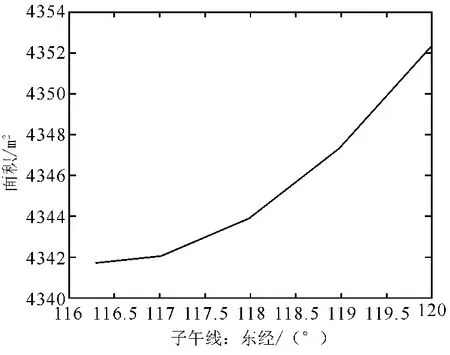
图4 湖心岛面积与经线设置

当选取子午线116.303 2°时计算面积为4 341.74m2，当选取子午线117°时计算面积为4 342.12m2，当选取子午线120°时计算面积为4 352.40m2.手持GPS自带“航线面积”功能计算的结果与选定中央子午线为120°所计算面积相吻合。

以子午线116.303 2°为基准，GPS所带面积计算功能所测面积与用公式（1）计算面积相比较，相对误差为0.23%.这是由于高斯投影长度变形的原因。

如图5所示，用公式（1）测量目标区域A′BC的面积，由于地球曲率的影响，实际所计算的却是区域A＇BC的面积。

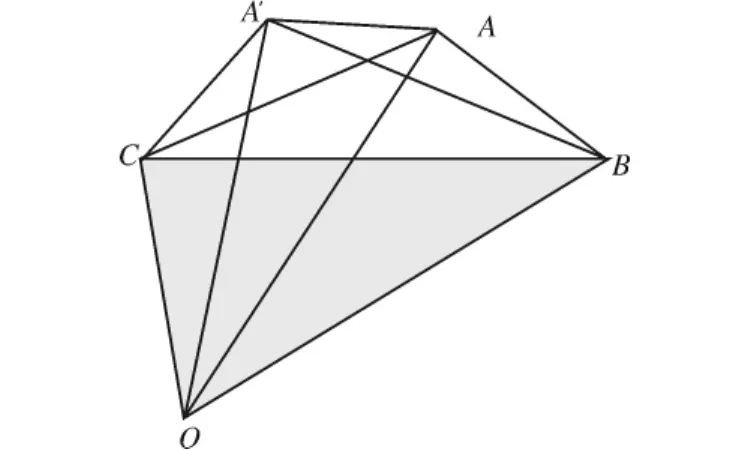
图5 面积变形与距离变形成正比

由于高斯投影在子午线方向没有长度变形，而高斯投影距离改化只与纬线方向参数y有关，所以在计算面积时，可以把所测区域按子午线方向分割成小块，这样立刻得出结论面积变形与距离改化成正比例关系。

即

相对误差为

设所测区域东西长度为u，所设经线距离所测区域最远点距离为v，以图3为例，则u＝Δy，v＝将地球平均半径Rm＝6 370km代入式（4）中，使用Matlab绘制误差曲面图，如图6所示。

图6 面积误差曲面图

由此可见，所选定经线距离所测区域越远，误差越大；所测区域越大，产生的误差越大。而区域ABC的面积修正函数

由式（5）可计算实际面积与所测面积关系曲面关系如图7所示。

测量目标区域距离120°，经线v＝315.35km，目标区域的东西最大长度u＝0.09km，以120°子午线为准计算面积为4 352.40m2，代入方程（4）和（5）中，得

测量目标区域距离117°，经线v＝59.52km，以117°子午线为准计算面积为4 342.12m2，代入方程（4）和（5）中，得

如图8所示。

图8 修正曲线

3.3 实验验证

使用相同的实验方法在北大静园做了一次实验。绕行静园一周，在拐点记录下航路点坐标，并使用MAP SOURCE软件将数据从手持GPS中导入计算机。航路点组成的航线可以直接在手持GPS中测量航线所围区域的面积。测量面积为3 655.604m2.如表2，3所示。

表2 GPS所测的各航路点坐标（静园）

表3 静园面积计算与修正

结果表明面积修正减小了误差。

4 结 论

分析了手持GPS测量面积的功能在坐标转换中产生的误差。原点（中央经线）距离所测区域越远，产生的误差越大；所测区域越大，产生的误差越大。所以应该对所计算结果加以修正，修正函数S或者在坐标转换时不刻板的选择中央子午线而是选择所测区域的平均经度，这样可以减小面积变形产生的误差。

为了得到比较精确的坐标，可以在测绘部门提供的坐标对手持GPS进行校正，再用GPS在同一点多次测量取平均的做法［13］。

若所测区域比较大时，可以采用分区域计算的方法。

［1］ 刘 弘，姚连芳，马 杰，等.GM－101型GPS面积测量与精度评价［J］.河南科技学院学报·自然科学版，2008，36（3）：33－35.

［2］ 夏友福.GPS测量面积的方法研究［J］.西南林学院学报，2005，25（1）：65－66.

［3］ 夏友福.手持GPS测量面积的精度分析［J］.西南林学院学报，2006，26（6）：59－60.

［4］ 郑成才.GPS林地面积测量精度分析［J］.武夷科学，2008（24）：110－113.

［5］ 黄献芳，向 磊，黄 萌.高斯投影面积在测量中的局限性研究［J］.光盘技术，2009（10）：46－47.

［6］ 谷超杰.Excel2003在高斯投影坐标换算中的应用［J］.测绘与空间地理信息，2008，31（6）：190－192.

［7］ 刘永义.济宁矿区BJ－54至WGS－84坐标转换模型改进及精度分析［J］.全球定位系统，2010，35（1）：33－37.

［8］ 赵廷安，田雪丰.矿区GPS高程拟合精度和可靠性研究［J］.中国煤田地质，2005，17（3）：59－60.

［9］ 晏 磊，苗李莉，刘岳峰.关于GPS技术在智能交通系统中的应用分析［J］.测绘通报，2005（8）：26－28.

［10］ 王可东，晏 磊，闻 辉.GPSOne应用于车载导航的可行性分析［J］.全球定位系统，2005，30（5）：35－39.

［11］ 施一民.现代大地控制测量［M］.北京：测绘出版社，2003.

［12］ 张秋昭，张书毕，刘 军.局部区域GPS网坐标转换的改进模型［J］.全球定位系统，2008，33（5）：62－64.

［13］ 周 蓓，陶彣君.手持GPS定位在野外地质测量中的误差分析［J］.资源环境与工程，2009，23（3）：311－313.