两种优化算法在反演断层滑动速率中的对比研究＊

李 鹏

（四川西南交大铁路发展有限公司，四川 成都610032）

0 引 言

通过地面大地测量数据反演大断裂的滑动速率等动态参数，从而通过地面观测到的地表变形来认识断层滑动的动力过程，是大地测量研究的主要问题之一。一般，在大地测量反演研究中，首先要根据实际问题选择一个近似地球物理模式，例如在震源参数反演中，一般采用弹性位错模式［1－2］。若选择的模型在理论上过于“真实”，由于数学处理困难，常使反演工作无法进行。因此，实际应用中必须在“模型”与“算法”之间取折衷方案。从数学的角度来看，反演是一个优化过程，就是要寻找一个能最好地解释观测数据的物理模型，使实际观测值与理论计算值的差异最小。

大地测量反演问题的算法，国内外的有关学者作了大量有意义的尝试，数值算法，尤其是优化反演方法的研究最为普遍，并取得了相当丰富的研究成果。如用Monte Carlo法或改进的Monte Carlo法反演断层参数［3－4］；利用水准测量资料结合遗传算法和最小二乘联合反演了共和地震的同震位错参数［5］；采用模拟退火法结合GPS和远场地震波资料对1999年台湾地震震源破裂过程进行了反演计算研究［6］。为了丰富大地测量数据反演问题的求解方法，将一种新的启发式算法——蚁群算法进行断层的参数反演，并基于位错模式，采用模拟的地面位移场，进行了断层三维滑动速率的反演，与传统的优化算法蒙特卡洛法反演的结果进行了比较，得出了蚁群算法的可靠性和稳定性优于蒙特卡洛法等结论。

1 反演理论与算法

在大地测量反演问题中，观测值与模型参数的关系常可表示为

式中：d为观测值；m为模型参数；G为联系观测值和模型参数的函数；Δ为观测误差。

在大地测量反演问题中，G通常是非线性的，所以反演是非线性反演。目标函数可表示为

式中：‖·‖2表示2－范数；E是目标函数值。

1.1 蒙特卡洛法

将反演过程中任何一个阶段，用随机（或伪随机）发生器产生模型、以实现模型全空间搜索的方法统称为蒙特卡洛反演法（MC）.

假如，已知待求模型参数的上下界限

有两种方法对模型空间进行搜索，一种是彻底搜索法，把模型空间允许的范围都搜索到，看哪一个模型，或哪一组模型的计算值和观测数据拟合最好。这种方法也叫穷举法；另一种搜索法是在模型空间允许的范围内随机地搜索，对每一个随机产生的模型计算其理论值并把它与观测值进行比较，看其是否可以接受，这就是传统的蒙特卡洛法。

1.2 蚁群算法

蚁群算法［8］（ACA）是一种崭新的仿生模拟进化算法，由Dorigo等人于20世纪90年代首先提出。ACA的思想是模拟蚂蚁寻食行为，使用大量的蚂蚁在搜索空间中随机搜索，并且用信息素来加强搜索路线，引导其他蚂蚁的搜索，同时引入信息素的挥发机制来避免陷入局部最优，这种引入挥发机制的正反馈使得该算法能够找到全局的多个最优解。

Dorigo等人充分利用蚁群搜索食物的过程与著名的旅行商问题 （TSP）之间的相似性，提出了蚁群算法，用人工蚂蚁模拟自然蚂蚁，通过模拟蚂蚁搜索食物的过程求解复杂的组合优化问题。一般地，可以用ACA在TSP的求解来说明ACA算法思想。

TSP是指对于给定的一组城市，设定其每两个城市之间的距离为已知，要求出一条总长度最小的封闭路线，该路线刚好只通过每个城市一次。记城市数为n，城市i与城市j之间的距离为dij（i，j＝1，2，…，n），蚂蚁数目为m，城市i与城市j之间路径上在t时刻的信息素量为τij（t），初始时刻每条路径上的信息素为τij（0）。蚂蚁k（k＝1，2，…，m）在面临路径选择的时候按照如下的转移概率来决定下一个去的城市

假设tabuk表示蚂蚁k已经访问过的城市列表，访问规则为每个城市只访问一次，所以要从可访问集合中删除已访问的城市，记allowedk＝｛N－tabuk｝为蚂蚁k还能去的城市集合。信息素更新规则为：蚂蚁在两个城市之间移动一步之后，都会增加城市之间路径上的信息素浓度，考虑到要防止快速陷入局部解，引入信息素挥发机制，所以一步之后更新为

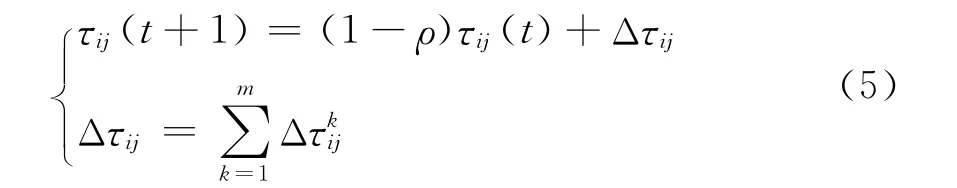
式中：ρ为信息素残留系数（0≤ρ≤1）；Δτij（t）和分别为蚁群与蚂蚁k在时间段t到（t＋1）内，在边（i，j）上留下的信息素浓度，Δτkij表示为

式中：Q为常量；Lk为蚂蚁k在本次循环中所选择路径的总长度。

参数Q，α，β，ρ的最佳组合可由实验确定［9］，在蚁群算法中，当路径稳定或者停止条件满足后，搜索结束。

2 算例及结果分析

为了验证两种优化算法的有效性和稳定性，基于位错模式，将位错理论模型［1－2］模拟计算的地面位移场作为观测值，模拟计算采用的某断层参数如表1所示。

表1中纬度、经度、H为断层起始端点坐标；U1、U2、U3为断层面上盘在走向、倾向和断层面法线方向的滑动量。L、W、D分别表示断层面的长度、宽度和下底面深度，A和f表示断层的走向和倾向。

表2示出了利用位错理论正演模拟计算得出的部分地面位移场。

表1 正演模拟断层参数

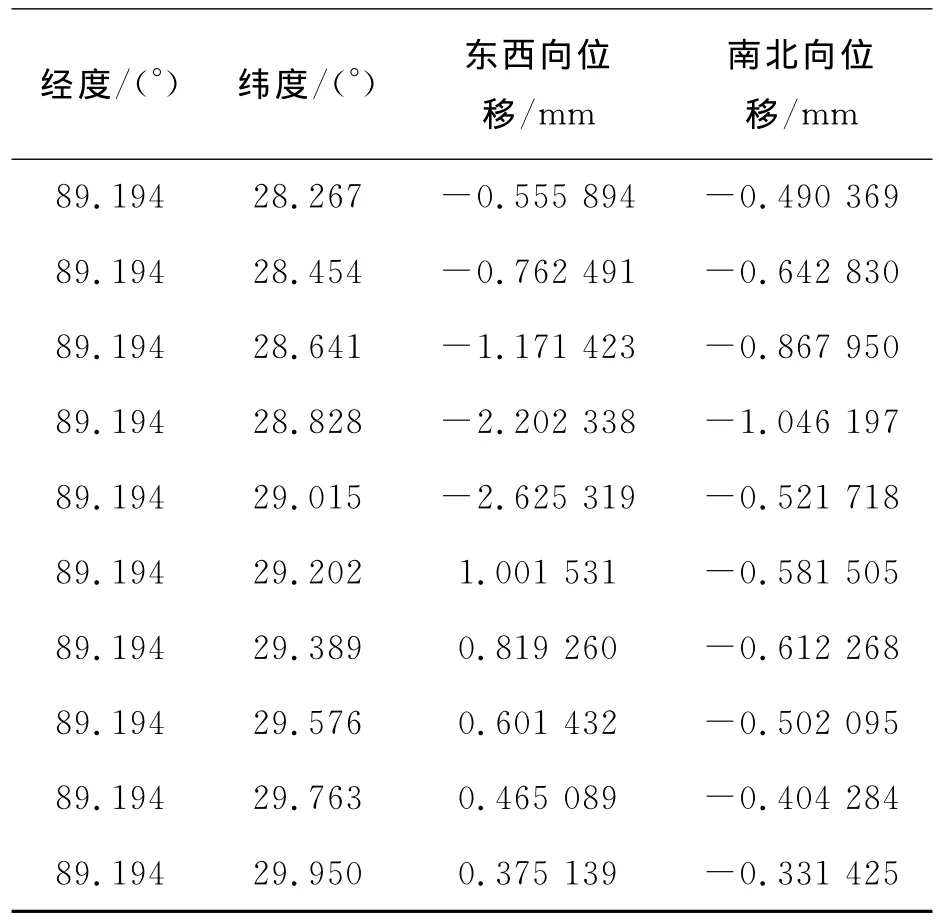
表2 部分正演模拟的地面水平位移

利用表2所示的模拟GPS的观测数据在断层的其它参数不变的情况下，对断层的三维滑动速率进行了反演计算分析，表2形式的模拟数据共527行，表2只示出了其中的一小部分；采用VB 6.0语言结合位错理论模型分别编制了蒙特卡洛法和蚁群算法反演的计算程序。

为了比较两种算法的可靠性和稳定性，在进行反演时，采用相同的取值范围，并且离散程度相同，计算相同的次数，共进行计算35次，3个待反演参数的取值范围如表3所示。

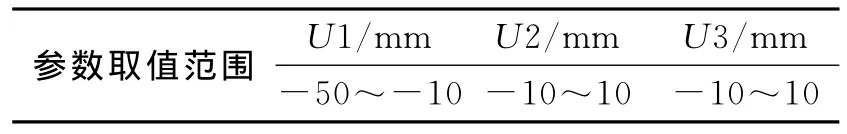
表3 待反演参数取值范围

蒙特卡洛法反演的基本过程简述如下：通过文件读入模拟GPS观测数据及观测点的坐标，确定每个参数的先验信息（即取值范围见表3），并将每个参数空间离散成10 000份，然后采用随机函数产生一组参数值。另外，由位错理论模型根据随机断层初始参数计算观测点的位移场，再由随机参数计算的位移场与模拟观测的位移场求出目标函数E，如果满足式（2）的约束条件，则输出反演结果。

蚁群算法反演的基本过程简述如下：通过文件读入断层初始参数和模拟GPS观测数据及观测点的坐标，将每个参数空间的取值在（表3）区间内离散成10 000份，采用随机函数产生一组参数值。另外，由位错理论模型根据随机断层初始参数计算观测点的位移场，再由随机参数计算的位移场与模拟观测的位移场求出目标函数E，并设蚂蚁k在某次循环中所选择路径的长度Lk＝E，由公式（4）～（6）建立蚁群算法的递推关系，最后由 （4）的大小来确定断层参数的更新，在实际计算中，由于参数之间不存在距离的概念，能见度ηij（t）取1进行计算。

表4分别示出了两种算法在进行35次计算中的一组最佳反演结果。

表4 MC和ACA的反演结果

图1、图2和图3分别为在上述取值范围和计算次数为35次的情况下，蒙特卡洛法和蚁群算法在断层三维滑动速率走滑、倾滑和张裂的反演计算结果对比图。从表4的结果以及图1、图2和图3所示的反演结果对比分析可以看出，蚁群算法得出的结果的稳定性和可靠性优于蒙特卡洛法。

图1 MC和ACA走滑反演值对比

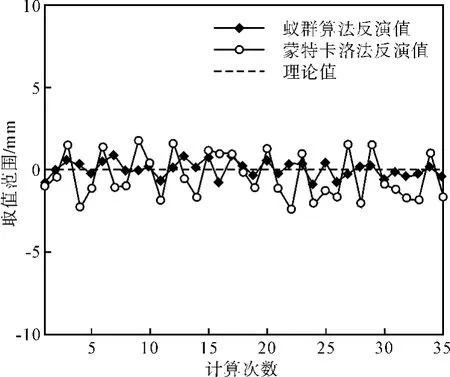
图2 MC和ACA倾滑反演值对比

图3 MC和ACA张裂反演值对比

3 结 论

通过理论分析和模拟GPS数据的反演计算分析，可得出以下结论：

1）蚁群算法在断层滑动速率反演结果中的稳定性和可靠性优于蒙特卡洛法，而且蒙特卡洛法在倾滑、张裂的反演值与理论值的偏离程度较大，明显差于蚁群算法。

2）算例的断层主要以走滑影响为主，因此，两种算法走滑的反演值与理论值的吻合程度较倾滑、张裂好些。

［1］ OKADA Y.Surface deformation due to shear and tensile faults in a half－space［J］.BSSA，1985（82）：1018－1040.

［2］ OKADA Y.Internal deformation due to shear and tensile faults in a half－space［J］.BSSA，1992（82）：1018－1040.

［3］ MURRAY M H，MARSHALL G A，LISOWSKI M，et al.The 1992M＝7Cape Mendocino，California，earthquake：coseismic deformation at the south end of the Cascadia megathrust［J］.J.Geophys.Res.1996，101（B8）：17707－17725.

［4］ FTEYMULLER J.Kinematics of the pacific－north America plate boundary zone，northern California［J］.J.Geophys.Res.，1999，104（B4）：7419－7441.

［5］ 王文萍，王庆良.利用遗传算法和最小二乘联合反演共和地震位错参数［J］.地震学报，1999，21（3）：285－290.

［6］ 王卫民，赵连锋，李 娟，等.1999年台湾集集地震震源破裂过程［J］.地球物理学报，2005，48（1）：132－147.

［7］ 王家映 .地球物理资料非线性反演方法讲座（二）蒙特卡洛法［J］.工程地球物理学报，2007，4（2）：81－85.

［8］ DORIGO M，MANIEZZO V，COLOMI A.The ant system：optimization by ant colony of cooperating agents［J］.IEEE Trans.Syst.Man.Cybern－PartB，1996，26（1）：29－41.

［9］ DORIGO M，GAMBARDELL L M.Ant colonies for the traveling salesman problem，bioSystems［J］.1997（43）：73－78.