天然肠衣搭配的数学优化模型

吴甬翔，金 敬

（宁波职业技术学院 公共教学部，浙江 宁波 315800）

天然肠衣搭配的数学优化模型

吴甬翔，金 敬

（宁波职业技术学院 公共教学部，浙江 宁波 315800）

[摘 要]以2011年高教社杯全国大学生数学建模竞赛赛题为背景，针对天然肠衣搭配问题，利用LINGO软件，建立关于天然肠衣组装成品捆数最多的线性规划模型和对应的原料搭配方案数学模型，求出各规格模型的最优解，提供各规格原料的具体搭配方案，使资源分配得到最优化，企业效益达到最大化。

[关键词]天然肠衣；搭配方案；数学模型；线性规划；LINGO软件

1 问题的提出

天然肠衣制作加工是我国一个传统产业，为提高生产效率，公司计划改变组装工艺，先丈量所有原料，建立一个原料表（见表1）；然后根据三种成品规格的要求（见表2），设计一个原料搭配方案，使工人根据这个方案“照方抓药”进行生产[1]。

公司对天然肠衣搭配方案有以下具体要求[1]：

（1）对于给定的一批原料，装出的成品捆数越多越好；

（2）对于成品捆数相同的方案，最短长度最长的成品越多，方案越好；

（3）为提高原料使用率，总长度允许有0.5m的误差，总根数允许比标准少1根；

（4）某种规格对应原料如果出现剩余，可以降级使用。如长度为14m的原料可以和长度介于7～13.5m的原料进行捆扎，成品属于7～13.5m的规格；

（5）为了食品保鲜，要求在30min内产生方案。

2 问题的分析

针对公司要求，在已知成品规格和原料情况下，设计符合要求的搭配方案，其实质是数学模型优化问题。由于原料出现剩余时可降级使用，为使原料能够充分利用，可以先把第三规格剩余的原料和第二规格剩余的原料拼在一起，按第二规格的要求建立模型进行原料的搭配，求出可以搭配的成品捆数。如果仍有剩余，则把剩余的原料和第一规格剩余的原料拼在一起，按第一规格的要求建立模型进行原料的搭配，求出可以搭配的成品捆数。因此，如何设计最优的搭配方案使原料按照三种成品规格进行组装,得到最多成

表1 原料描述

表2 成品规格

3 模型假设与符号说明

3.1 模型假设

天然肠衣制作加工的环境有良好通风条件，有适宜温度；整个原料搭配过程中肠衣没有受到损坏；生产出来的都是合格的成品肠衣；原料的摆放分类明确，不会出现混淆情况[3]。

3.2 符号说明

F表示成品捆数；f1，f2，f3分别为第一规格搭配的成品捆数、第二规格搭配的成品捆数、第三规格搭配的成品捆数；ai（i=1，2，3，…，8）表示3～6.5m中每档原有根数；bj（j=1，2，3，…，14）表示7～13.5m中每档原有根数；ck（k=1，2，3，…，24）表示14～25.5m中每档原有根数；xi（i=1，2，3，…，8）表示3～6.5m中每档抽取根数；yj（j=1，2，3，…，14）表示7～13.5m每档抽取根数；zk（k=1，2，3，…，24）表示14～25.5m每档抽取根数。

4 模型的建立与求解

4.1 各规格原料组装成品捆数最多的线性规划模型

由于要保证每捆长度为89m，为提高原料使用率，每捆总长度允许有±0.5m的误差，而且总根数允许比标准少1根，因此得到线性规划模型为：

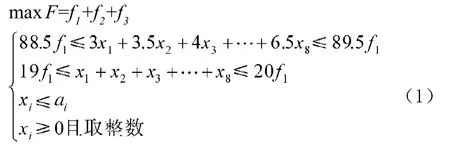
每种规格对应原料如果出现搭配剩余可以降级使用，因此从（3）式开始计算。利用LINGO[4-5]软件解得第三规格可搭配的成品捆数f3=137，同时得到每档所需根数为：z1=35，z2=29，z3=30，z4=42，z5=28，z6=42，z7=45，z8=49，z9=50，z10=64，z11=52，z12=63，z13=49，z14=35，z15=27，z16=16，z17=12，z18=2，z19=0，z20=5，z21=0，z22=0，z23=0，z24=1。

定向越野运动不但考验学生的身体素质，对其综合能力也是一种考验。如，在开展定向越野运动时，首先，教师可多设定几条不同路线，并在不同路线上设置多个不同的目标，路线的选择与最终的成绩相关联，在这个思考、分析和选择的过程中，学生的综合能力也会得到相应的锻炼与提高。其次，教师可在地图上设置一些陷阱目标，从而锻炼学生的分析能力、选择能力和决断能力，这对学生未来的发展具有积极意义。

与原料表相比较，z20（档次为23.5～23.9m）剩余1根。把z20剩余的一根降级到第二规格进行搭配，利用LINGO软件解得第二规格可搭配的成品捆数f2=37，同时得到每档所需根数y1=0，y2=6，y3=4，y4=25，y5=21，y6=23，y7=21，y8=18，y9=31，y10=23，y11=22，y12=59，y13=18，y14=25，y20=0。y1（档次为7～7.4m），y2（档次为7.5～7.9m），y3（档次为8～8.4m），z20（档次为23.5～23.9m）分别剩余24、18、16、1根。再把剩余根数降级到第一规格进行搭配，利用LINGO软件解得第一规格可搭配的成品捆数f1=16，同时得到每档所需根数x1=43，x2=59，x3=39，x4=41，x5=27，x6=28，x7=34，x8=20，y1=19，y2=0，y3=0，z20=0。x8（档次为6.5～6.9m），y1（档次为7～7.4m），y2（档次为7.5～7.9m），y3（档次为8～8.4m），z20（档次为23.5～23.9m）分别剩余1、5、18、16、1根。最后将剩余根数进行检验，分别按第一、二规格运算，经过验证无解，则不可再搭配成捆。因此，天然肠衣组装成品捆数最多为max F=f1+f2+f3=16+37 +137=190。

4.2 各规格原料搭配的数学模型

根据天然肠衣最多组装的成品捆数，利用线性方程组，建立各规格原料搭配的数学模型。

第一规格每捆原料搭配的数学模型为：

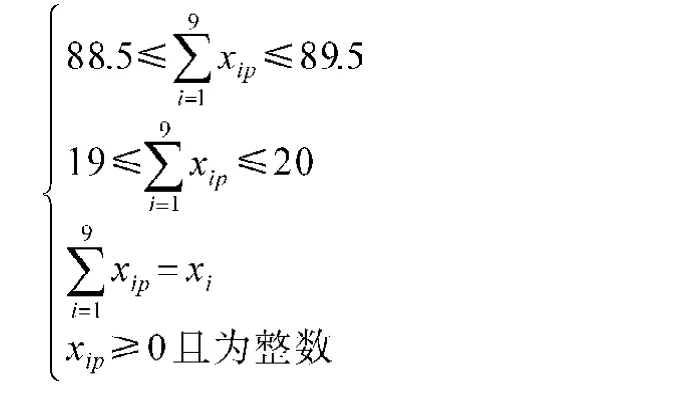
其中，xip表示从每捆每档中抽取的根数，p表示第几捆（i=1，2，3，…，9；p=1，2，3，…，16）。利用LINGO软件计算得到第一规格原料搭配方案（见表3）。

表3 第一规格原料搭配方案

第二规格每捆原料搭配的数学模型为：

第三规格每捆原料搭配的数学模型为：

其中，zkg表示从每捆每档中抽取的根数，g表示第几捆（k=1，2，3，…，24；g=1，2，3，…，137）。利用LINGO软件计算得到第三规格原料搭配方案（见表5）。

表4 第二规格原料搭配方案

表5 第三规格原料搭配方案

5 结 论

按照公司对天然肠衣搭配方案的具体要求，先丈量所有原料，建立原料表，然后采用线性规划模型和数学优化模型，利用LINGO软件计算即可得到三种规格原料的具体搭配方案，这可以使工人根据最优方案“照方抓药”进行生产，节省时间，满足30min产生方案的要求。该数学优化模型研究的是生产加工过程中分拣组装的实际问题。通过利用LINGO软件，可以降低计算难度，提高工作效率，准确快速地得出合理优化的搭配方案。对于生产过程中原料损耗等问题，一些参数可以依据实际情况而设定。因此，该数学优化模型对于提高工作效率和生产效率具有普遍性和实用性。

[参 考 文 献]

[1]中国工业与应用数学学会.2011年高教社杯全国大学生数学建模竞赛赛题[EB/OL].(2011-09-09)[2012-09-15]. http://www.mcm.edu.cn/html_cn/node/a1ffc4c5587c8a6f96eacefb8dbcc34e.html.

[2]石国春，唐玉鹏，王鹏飞，等.天然肠衣搭配问题[J].兰州工业高等专科学校学报，2012，19(3):60-63.

[3]中国天然肠衣出口指南[EB/OL].(2005-02-19)[2012-09-15].http://wenku.baidu.com/view/0c3fcf80e53a580216fcfe21.html.

[4]试锋芒.Lindo&Lingo教程[EB/OL].(2010-04-30)[2012-09-15].http://wenku.baidu.com/view/f7149dc24028915f804dc22b.html.

[5]谢金星，薛毅.优化建模与LINGO/LINGO软件[M].北京:清华大学出版社，2005:11-15.

[责任编辑：宣 明]

[中图分类号]O224

[文献标识码]A

[文章编号]1671-4326(2012)04-0048-03

[收稿日期]2012-09-26

[作者简介]吴甬翔（1976—），女，浙江宁波人，宁波职业技术学院公共教学部讲师；金 敬（1968—），女，浙江宁波人，宁波职业技术学院公共教学部讲师.品捆数，是解决该问题的关键。通过利用线性规划模型和数学优化模型，建立目标函数，结合LINGO软件求出各规格模型的最优解[2]。

Mathematical Optimization Model of Natural Casing Match

WU Yongxiang, JIN Jing
(Public Courses Department, Ningbo Vocational and Technical College, Ningbo, 315800, China)

Abstract:On the background of 2011 National College Mathematical Modeling Contest of Higher Education Cup, a linear programming model with the most finished bundle number of natural casing and a corresponding mathematical model of material matching scheme are set up in terms of the match problem of the natural casing by using the LINGO software. The purpose is to work out the best solution to various models and provide the specific matching scheme to obtain the optimization both in the source allocation and the company benefit.

Key words:Natural casing; Matching scheme; Mathematical model; Linear programming; LINGO software