复杂条件下黏性土主动土压力解析解

杨 剑

(上海市政工程设计研究总院第二设计院,上海 200092)

挡土墙土压力一直是工程和学术界最重要、最基本的问题之一。虽然不断有学者尝试用新方法求解土压力,但基于极限平衡理论的Rankine土压力理论和Coulomb土压力理论仍是实际工程中应用最为广泛的方法[1]。以上两种基本理论都有其适用范围,Rankine土压力理论可求解挡土墙背竖直、填土表面水平的黏性土土压力问题,而Coulomb理论则适用于无黏性土情况。然而,实际工程遇到的经常是综合了Rankine和Coulomb两种土压力理论求解范围的复杂问题,因此,对挡土墙背倾斜、填土表面倾斜等复杂条件下黏性土的土压力进行研究更具有实际意义。

Morrison等[2]通过极限平衡分析得到了挡土墙主动土压力;Soubra等[3-4]利用极限分析法得到了挡土墙主动土压力;Wang[5]基于极限平衡分析的水平层法得到了挡土墙主动土压力系数和分布。以上分析都是以砂土为研究对象的。

Subba等[6]利用极限平衡分析得到了黏性土的主动土压力系数,考虑了由对数螺旋线组成的复合滑裂面,但推导过程较复杂,不便于工程应用;李巨文等[7]根据Coulomb土压力的计算原理,从滑动楔体处于极限平衡状态时的静力平衡条件出发,推导了计算黏性土主动土压力的公式,但未考虑黏性土开裂及填土与挡土墙背界面黏着力对土压力的影响;卢廷浩[8]考虑滑裂面上填土的黏聚力及填土与墙背接触面上的黏着力,得到了黏性填土挡墙上的主动土压力计算公式,但并未考虑黏性土开裂的影响;狄圣杰等[9]基于Coulomb理论的平面滑裂面假设,考虑滑裂面上填土的黏聚力和填土与挡土墙背之间的黏着力,利用库尔曼图解法求得了主动土压力和破坏面倾角,但未深入考虑黏土开裂的影响;林智勇等[10]基于库仑理论的平面滑裂面假设,考虑填土黏聚力及填土和墙背间的黏着力,利用水平层法导出了作用在挡土墙上主动土压力的解析解,可以考虑黏性土开裂对主动土压力的影响,但并未作深入的分析;胡晓军等[11-12]基于Coulomb理论的平面滑裂面假设,考虑滑裂面上填土黏聚力及填土与挡土墙背接触面上黏着力,分别对黏性土主动和被动土压力的Coulomb解算法进行了改进,可处理超载及裂缝深度等较复杂的工况,但并未作裂缝开展深度及挡土墙背黏着力对土压力影响的分析。

本研究基于极限平衡理论及Coulomb土压力理论,在相关研究的基础上,对挡土墙达到主动极限状态下的黏性填土进行分析,考虑了挡土墙倾角、填土摩擦角、填土黏聚力、挡土墙背与土界面摩擦角、挡土墙背与土界面黏着力、黏性填土表面坡角、黏性土表面裂缝深度对黏性土主动土压力的影响,通过推导得到了以黏性土质量分量、超载分量、黏聚力分量主动土压力系数表示的黏性土主动土压力计算公式。

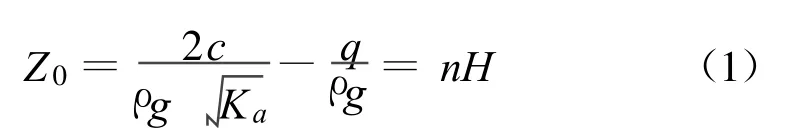
1 分析模型

图1表示一倾斜挡土墙达到主动极限平衡状态时作用在破坏土楔上的力。图1中,H为挡土墙AB的高度,h为填土出现裂缝以后的高度,α为挡土墙AB与竖直方向的夹角,β为墙后黏性填土的坡角,θ为破坏土楔与水平方向的破裂角,φ为土体的摩擦角,W为土楔自重;c为土体黏聚力,δ为土体与挡土墙背的摩擦角,cw为土体与挡土墙背的黏着力,Pa为主动土压力,R为土体对破坏土楔的反力;Z0为裂缝深度。

倾斜填土表面AD作用有均布超载压力q。假设黏性填土表面出现受拉裂缝,且裂缝深度为Z0,根据Rankine土压力理论,近似确定裂缝深度的表达式为

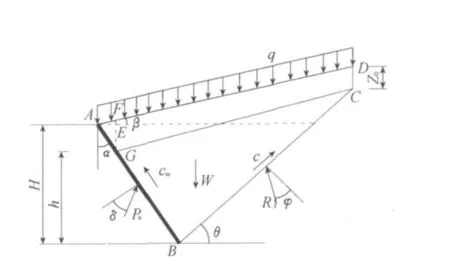
图1 土体极限平衡时作用在破坏土楔上的力Fig.1 Forces acting on failurewedgein active state under limit equilibrium conditions

式中：ρ——填土密度;Ka——Rankine主动土压力系数;g——重力加速度;n——黏土开裂深度系数,为无量纲系数,取值范围为0～1;Z0≤0时,取Z0=0。

由图1,对△AGF根据正弦定理可得

对△GBC,由正弦定理可得

令

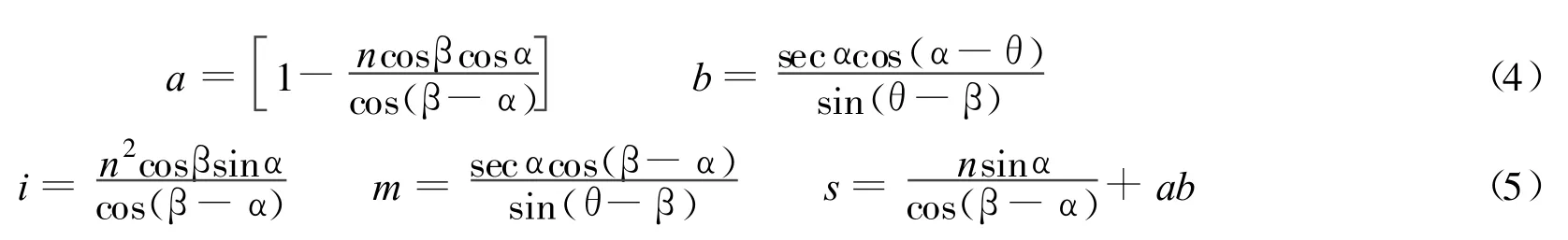
可得

2 破坏土楔受力分析

a.土楔ABCD的自重W。计算公式为

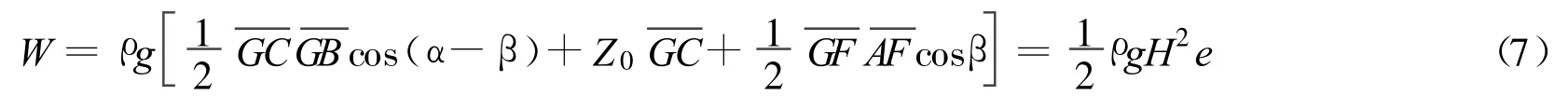
其中

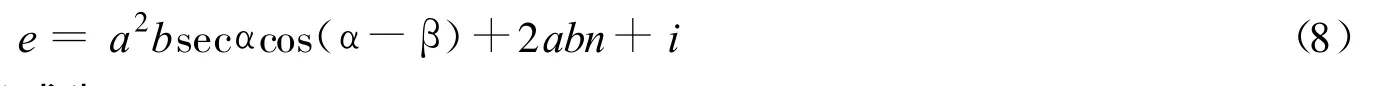
b.均布超载的合力Q。计算公式为

c.土体破裂面BC上的总黏聚力C。计算公式为

d.挡土墙背的总黏着力Cw。计算公式为

对图1,由竖直方向力的平衡条件,有

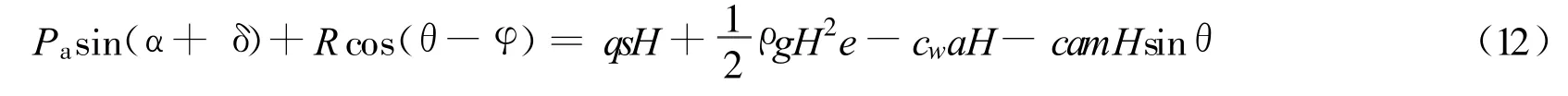
由水平方向力的平衡条件,有

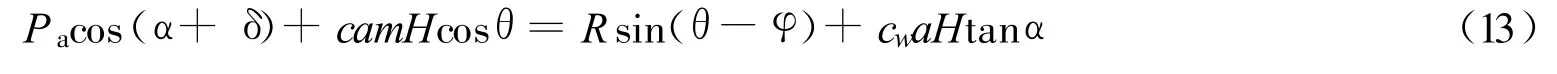
联立式(12)和式(13),消去反力R,整理得

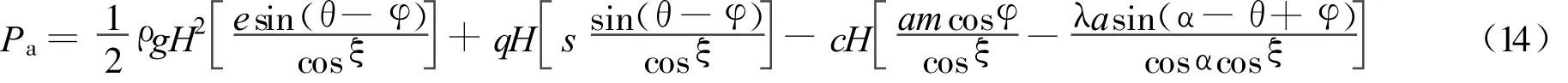
其中

式中,λ为填土和墙背之间的黏着力cw与土体黏聚力c之间的系数,取值在0～1之间。

式(14)可写为如下形式：

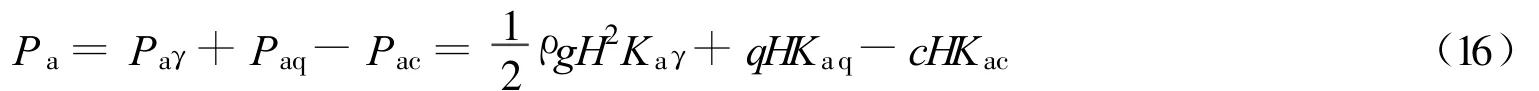
其中

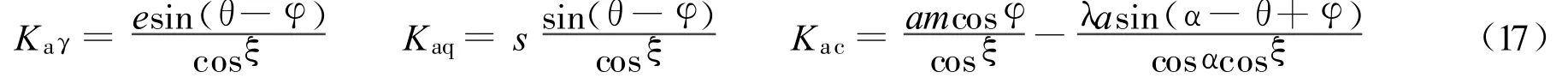
式(16)形如求解黏性土主动土压力的Rankine公式,其中Kaγ,Kaq,Kac分别是对应于土体质量分量、超载分量和黏聚力分量的主动土压力系数。由式(16)可以看出,主动土压力Pa分为3个部分,分别是：(a)单位土体质量分量Paγ(ρg≠0,c=q=0);(b)超载分量Paq(q≠0,c=ρg=0);(c)黏聚力分量Pac(c≠0,q=ρg=0)。为了得到最大主动土压力,对于黏性土的以上3个分量,可分别求土体质量分量的最大主动土压力、超载分量的最大主动土压力、黏聚力分量的最小主动土压力,然后将3者叠加即可得到综合考虑了填土面超载和黏聚力的黏性土最大主动土压力。令黏聚力分量为零,公式即退化为Coulomb条件下无黏性土主动土压力。

3 黏性土主动土压力系数

关于土体质量分量Paγ、超载分量Paq、黏聚力分量Pac的主动土压力,只有土体达到极限平衡状态时破裂面倾角θ为未知,这时,可用Coulomb土压力理论求滑裂面的通常做法,分别令土压力各分量的dP/dθ=0,即可求得各自分量对应的极限滑动面位置,进而得到相应的主动土压力。

3.1 土体质量分量主动土压力系数Kaγ(ρg≠0,c=q=0)

有了土体滑裂面破裂角θ,根据式(17)可求得土体质量分量主动土压力系数Kaγ。表1为不考虑黏性土开裂深度的土体质量分量的主动土压力系数Kaγ。由表1可以看出,随着倾斜挡土墙倾角 α由负为正,Kaγ逐渐增加;随土体内摩擦角φ及挡土墙背与土体摩擦角δ的增加,Kaγ减小,但土体内摩擦角对Kaγ的影响更明显;随填土坡角β的增加,Kaγ也增加。

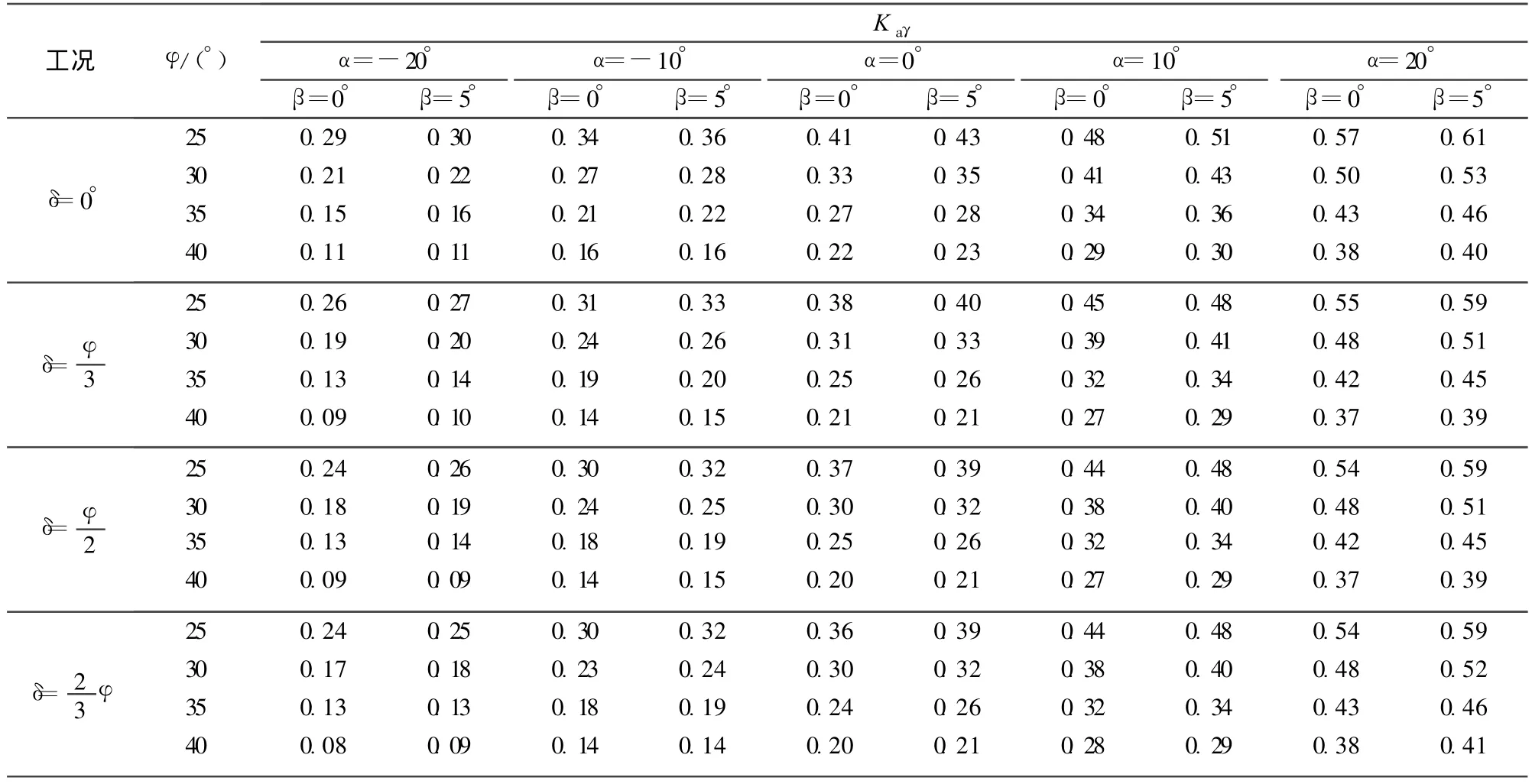
表1 土体质量分量主动土压力系数Kaγ(n=0)Table1 Coefficients of active earth pressure Kaγ(n=0)

3.2 超载分量主动土压力系数Kaq(q≠0,c=ρg=0)

表2为不考虑黏性土裂缝开展深度的超载分量主动土压力系数Kaq。随着α由负为正,Kaq逐渐增加;随着 δ及φ的增加,Kaq减小;随 β的增加,Kaq增加。

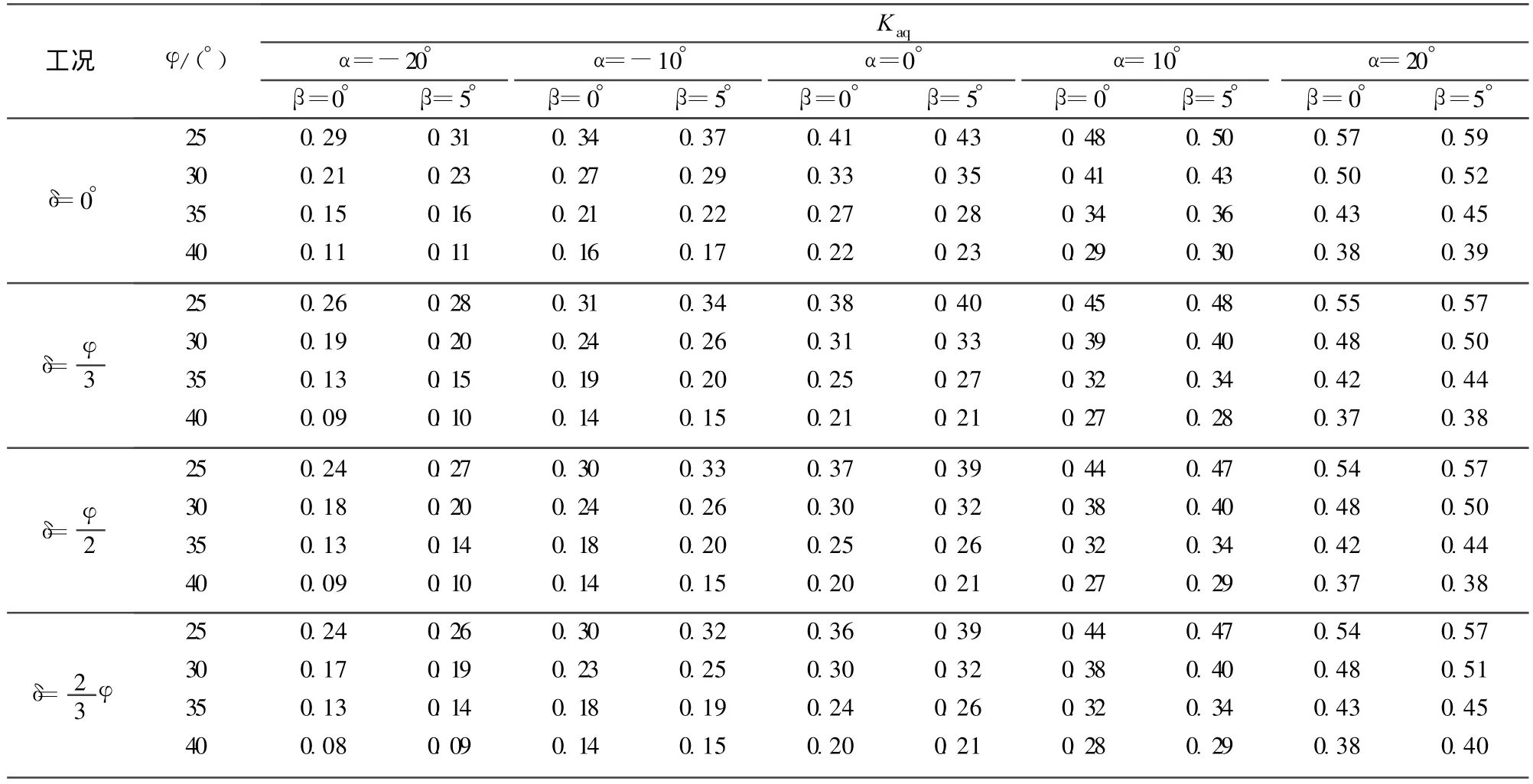
表2 超载分量主动土压力系数Kaq(n=0)Table2 Coefficients of active earth pressure Kaq(n=0)

3.3 黏聚力分量主动土压力系数Kac(c≠0,q=ρg=0)

表3为不考虑黏性土裂缝开展深度及挡土墙背黏着力的黏聚力分量主动土压力系数Kac。随着α由负为正,Kac逐渐减小,随 δ及φ的增加,Kac也减小;随 β的增加,Kac增加。

3.4 挡土墙背与土体界面黏着力对黏聚力分量主动土压力系数的影响

图2表示土体黏聚力c一定的条件下,通过系数λ的变化来体现挡土墙背与土体界面黏着力对黏聚力分量主动土压力系数的影响。从图2可以看出,随着挡土墙背与土体界面黏着力的增加,黏聚力分量主动土压力系数也逐渐增加。

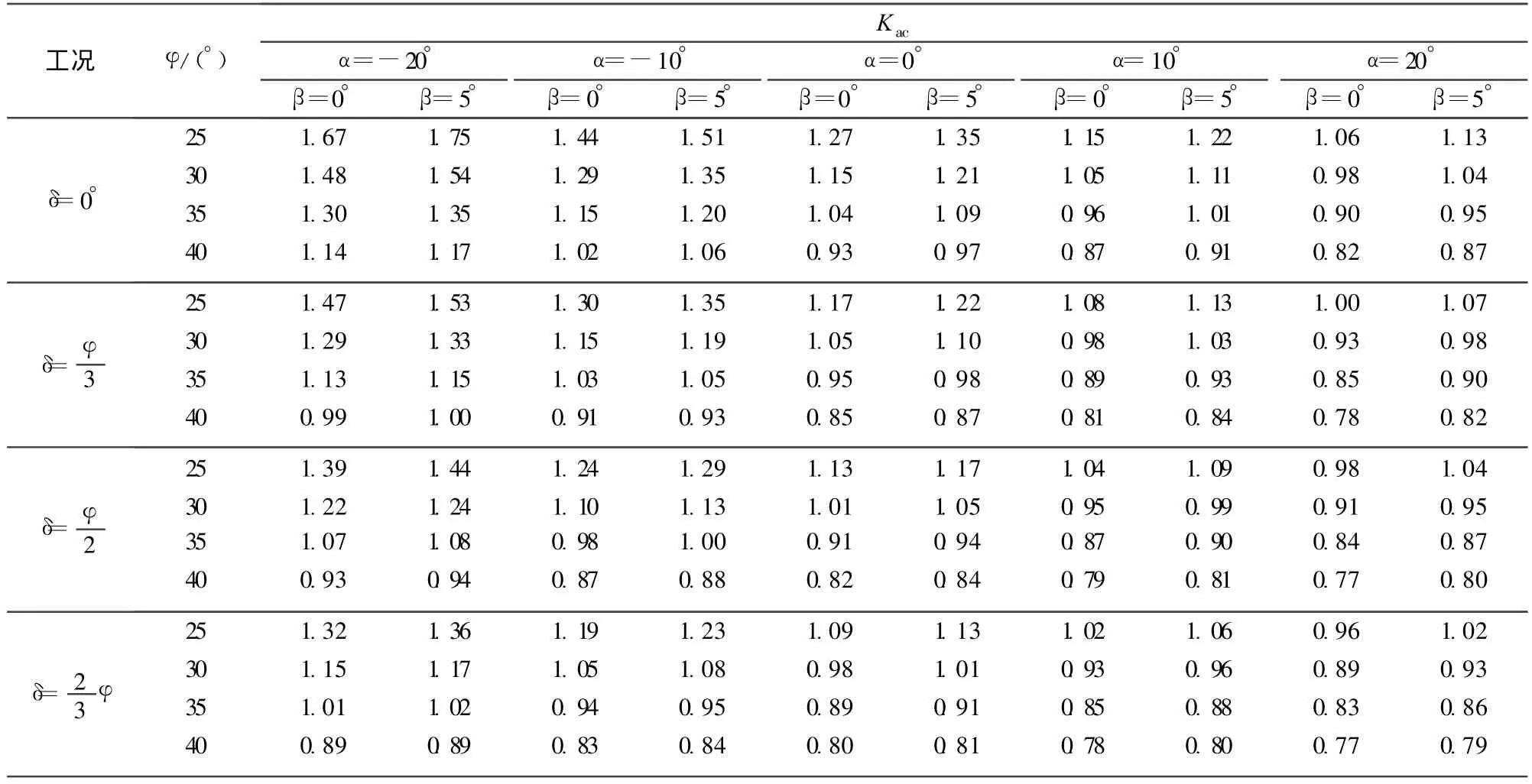
表3 黏聚力分量主动土压力系数Kac(n=0,λ=0)Table3 Coefficients of active earth pressure Kac(n=0,λ=0)

3.5 裂缝开展深度对主动土压力系数的影响

设挡土墙密度ρ=2t/m3,黏聚力c=10kPa,超载力q=10kPa,根据式(1)可确定不同填土摩擦角下的裂缝开展深度,裂缝开展深度对土压力的影响是随挡土墙高度而变化的。为了综合考虑裂缝开展深度对挡土墙土压力的影响,本研究通过变化填土摩擦角 φ和挡土墙高度H,用黏性土裂缝开展深度系数n变化来反映裂缝开展深度对主动土压力系数的影响,见表4。

由表4可以看出,φ越大,裂缝开展深度系数n越大;同等条件下,挡土墙越高,裂缝开展深度系数越小。由图3、图4及图5可以看出,随着裂缝开展深度的增加,黏性土单位质量分量、超载分量、黏聚力分量的主动土压力系数都减小。

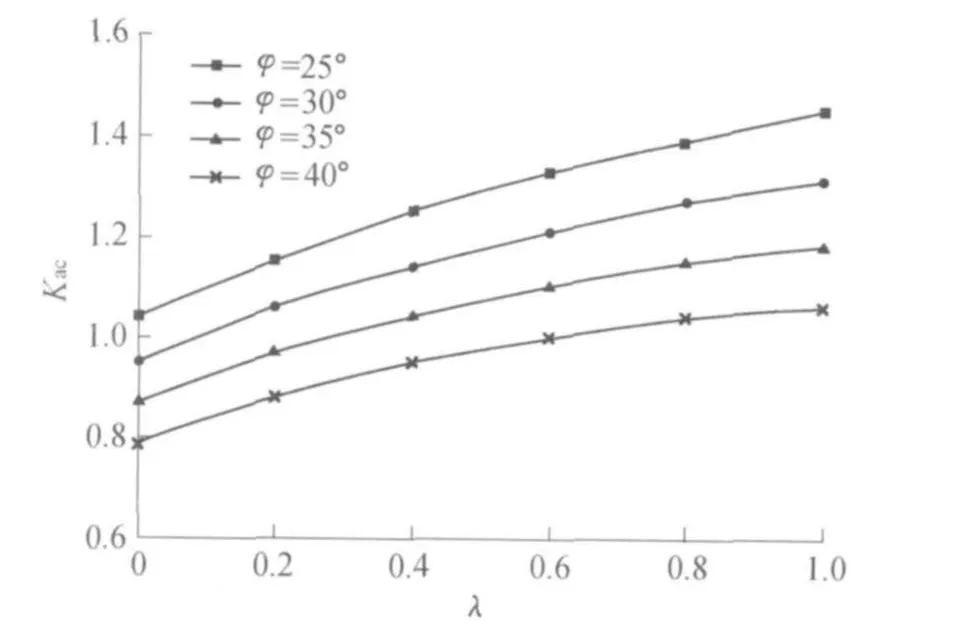
图2 λ对Kac的影响(α=10°,β=0°,δ=φ/2)Fig.2 Influence ofλon coefficient Kac(α=10°,β=0°,δ=φ/2)

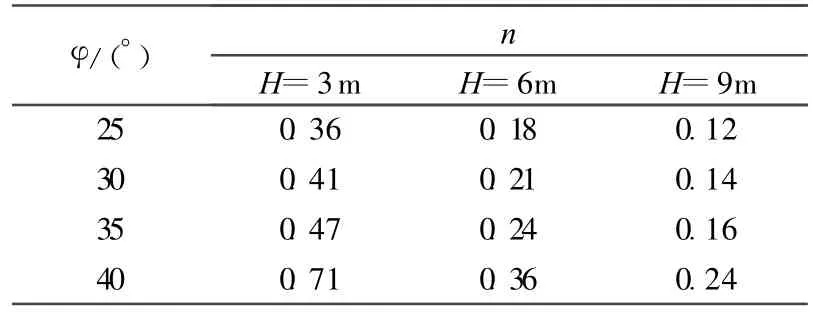
表4 不同摩擦角及挡土墙高度下裂缝开展深度系数nTable4 Crack coefficient n at different friction angles and with different retaining wall heights

4 本文解与相关成果的对比

算例1 为了验证本文解的合理性,首先与Rankine土压力理论计算公式进行对比。本文解是基于Coulomb土压力理论得出的,当挡土墙倾角及填土坡角为零时,公式即退化为黏性土Rankine主动土压力计算条件。黏性土Rankine主动土压力的计算公式为

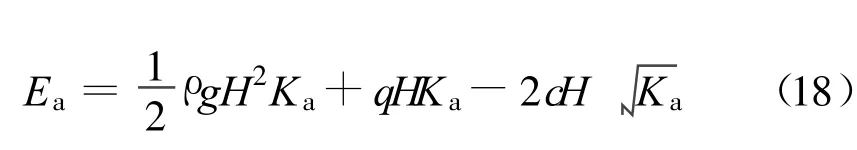
式中Ka为主动土压力系数,Ka=tan2(45-φ/2)。

从表5可以看出,本文解与Rankine土压力理论是完全一致的,也说明了本文解的合理性。

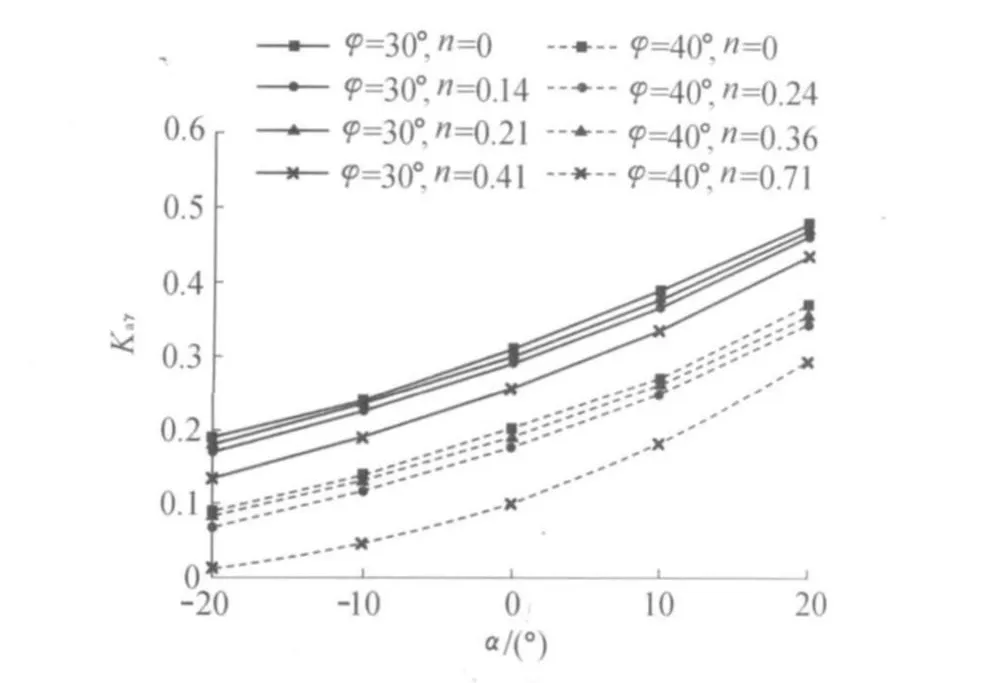
图3 系数n对Kaγ的影响(δ=φ/3,β=0°)Fig.3 Influence of n on coefficient Kaγ(δ=φ/3,β=0°)

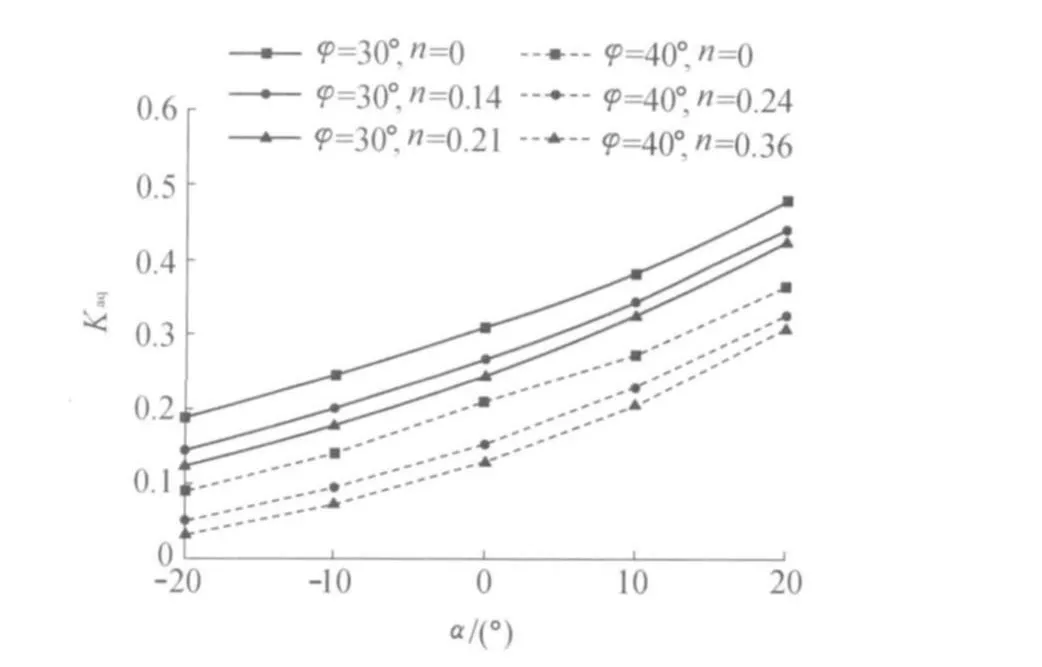
图4 系数n对Kaq的影响(δ=φ/3,β=0°)Fig.4 Influence of n on coefficient Kaq(δ=φ/3,β=0°)

算例2 某挡土墙高H=10m[8,11],墙后填土参数为：ρ=1.86t/m3,φ=24°,填土表面无超载,土体黏聚力及挡土墙背与土体界面黏着力如表6所示。

由表6可以看出,本文解与文献[9-10]计算结果很接近,同时,在满足Rankine和Coulomb土压力理论条件下,本文解的计算结果与经典理论解是完全一致的。

算例3 某挡土墙高H=4.6m[11],墙面垂直,墙后填土为黏性土,ρ=1.93t/m3,c=10kPa,φ=15°,δ=10°,β=0°,填土表面作用均布超载q=10kN/m,计算结果见表7。

由表7可以看出,无论考虑裂缝或不考虑裂缝,本文解的计算结果都要优于文献[11,13]方法的计算结果,与实测值的结果更接近。

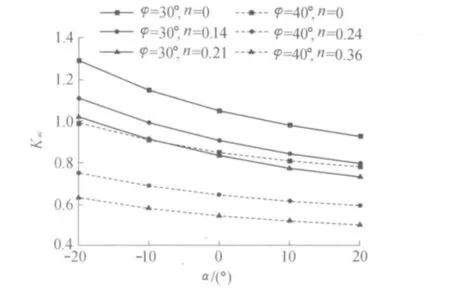
图5 系数n对Kac的影响(δ=φ/3,β=0°)Fig.5 Influence of n on coefficient Kac(δ=φ/3,β=0°)

表5 本文解与Rankine理论计算的黏性土主动土压力结果对比Table5 Comparison of active earth pressure of cohesive soil between Rankine theory and proposed method

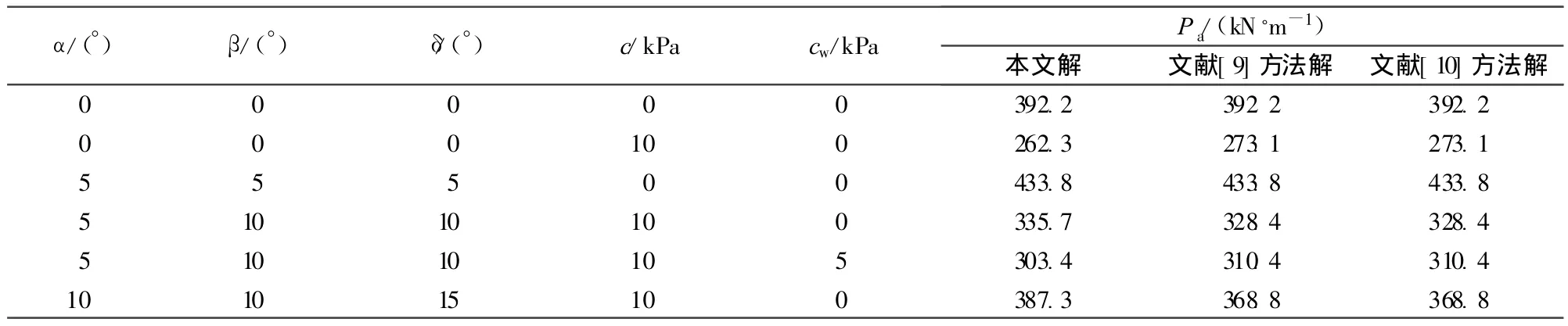
表6 算例2本文解与相关文献解结果比较Table 6 Comparison of results of Case2 for active earth pressure calculation and relevant references

5 结 论

基于极限平衡理论及Coulomb土压力理论,对挡土墙达到主动极限状态下的黏性填土进行分析,考虑挡土墙倾角、填土摩擦角、填土黏聚力、挡土墙背与土界面摩擦角和黏着力、黏性填土表面坡角、黏性土表面裂缝深度对黏性土主动土压力的影响,通过推导得出以黏性土质量分量、超载分量、黏聚力分量主动土压力所表示的黏性土主动土压力。虽然用Rankine土压力理论黏性土裂缝计算公式考虑Coulomb条件下裂缝开展深度有一定的误差,但还是比较好地反映了黏性土开裂对主动土压力的影响,与实测结果更接近。

在特定条件下,本文解与经典的Rankine和Coulomb土压力理论计算结果是完全一致的,且既适用于黏性土,也适用于砂土,公式简洁,推导严密,计算结果可靠,可应用于实际工程,方便工程技术人员掌握。

表7 算例3本文解计算结果与相关文献及实测结果比较Table7 Comparison of results of Case 3 for active earth pressure calculation,relevant references,and observation

[1]王元战,李新国,陈楠楠.挡土墙主动土压力分布与侧压力系数[J].岩土力学,2005,26(7)：1019-1022.(WANG Yuanzhan,LI Xinguo,CHENNannan.Active earth pressureon a retainingwall and lateral coefficient of earth pressure[J].RocKand Soil Mechanics,2005,26(7)：1019-1022.(in Chinese))

[2]MORRISON E E,EBELING RM.Limit equilibrium computationof dynamic passive earth pressure[J].Canadian Geotechnical Journal,1995,32：481-487.

[3]SOUBRA A H.Static and seismic passive earth pressure coefficients on rigid retaining structures[J].Canadian Geotechnical Journal,2000,37：463-478.

[4]KUMARJ.Seismic passive earth pressure coefficients for sands[J].Canadian Geotechnical Journal,2001,38：876-881.

[5]WANG Y Z.Distribution of earth pressure on a retainingwall[J].Geotechnique,2000,50(1)：83-88.

[6]SUBBA R KS,CHOUDHURY D.Seismic passive earth pressures in soils[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,31：131-135.

[7]李巨文,王翀,梁永朵,等.挡土墙后黏性填土的主动土压力计算[J].岩土工程学报,2006,28(5)：650-652.(LI Juwen,WANG Chong,LIANG Yongduo,et al.Computation of earth pressureof cohesive backfill on retainingwall[J].Chinese Journal of Geotechnical Engineering,2006,28(5)：650-652.(in Chinese))

[8]卢廷浩.考虑黏聚力及墙背黏着力的主动土压力公式[J].岩土力学,2002,23(4)：470-473.(LU Tinghao.A formula of active earth pressure including cohesion and adhesion[J].RocKand Soil Mechanics,2002,23(4)：470-473.(in Chinese))

[9]狄圣杰,徐卫亚.黏性土主动土压力的库尔曼法及应用[J].岩土工程学报,2010,32(6)：970-974.(DI Shengjie,XU Weiya.Culmann's method for activeearthpressureof cohesive soil and itsapplication[J].Chinese Journal of Geotechnical Engineering,2010,32(6)：970-974.(in Chinese))

[10]林智勇,戴自航,苏美选.复杂条件下挡土墙主动土压力解析解[J].岩土工程学报,2008,30(4)：556-559.(LIN Zhiyong,DAI Zihang,SU Meixuan.Analytical solution of active earth pressure acting on retaining walls under complicated conditions[J].Chinese Journal of Geotechnical Engineering,2008,30(4)：556-559.(in Chinese))

[11]胡晓军.黏性土主动土压力库仑精确解的改进[J].岩土工程学报,2006,28(8)：1049-1052.(HU Xiaojun.Improvement on Coulomb accuratesolution of active earth pressureto cohesivesoil[J].Chinese Journal of Geotechnical Engineering,2006,28(8)：1049-1052.(in Chinese))

[12]胡晓军,谭晓慧.黏性土被动土压力计算的库仑数值解[J].河海大学学报：自然科学版,2009,37(3)：304-307.(HU Xiaojun,TAN Xiaohui.Coulomb numerical solution of passive earth pressure on cohesive soil[J].Journal of Hohai University：Natural Sciences,2009,37(3)：304-307.(in Chinese))

[13]顾慰慈.黏性土主动土压力计算[J].水利学报,1991(2)：55-64.(GU Weici.Calculation of active earth pressure for cohesive soil[J].Journal of Hydraulic Engineering,1991(2)：55-64.(in Chinese))