大跨度斜拉桥钢桥塔基于涡振的气动选型及驰振性能风洞试验研究
李永乐,廖海黎,李佳圣,覃 红
(西南交通大学桥梁工程系,成都 610031)
0 引 言
随着中国桥梁工程的迅速发展,桥梁跨度越来越大,桥塔也随之越来越高。桥塔作为一种高柔结构,风荷载是作用于其上的主要横向荷载,因此桥塔日益增高的趋势必然会加大风荷载的作用力度[1]。大跨度桥梁的桥塔在施工和运营阶段时,高耸的桥塔在自然风的作用下会发生涡激振动和驰振。相对于混凝土桥塔,钢制桥塔具有质量轻、阻尼小等特点,在常见风速下也易产生较大的振幅,严重影响施工人员和维护人员的舒适性,甚至危及结构安全。为确保大跨度桥梁钢桥塔在施工阶段和成桥运营后的安全,在钢桥塔设计时有必要对其进行气动选型及风致响应研究。
已有的桥梁气动选型和风致响应研究较多地集中于主梁截面[2-4],钢桥塔在国内应用较少[5],相关研究报道较为少见。Takeuchi[6]针对自由竖立的钢桥塔容易出现涡激振动的特点,采用风洞试验的方法来考察钢桥塔的气动特性和涡激振动发生机制,并结合前人研究成果与风洞试验,研究了串联双柱式桥塔的气动稳定性,通过合理布置双肢塔柱的突出附属物、塔柱截面的切角数量、来流风向角以及两塔柱的间距比等参数可改善桥塔的气动稳定性。Larose等[7]针对376m高的H形钢桥塔首先进行了两阶段的节段模型试验来选取较优截面,再通过1/250的气弹模型试验选取最优截面,并指出涡激振动是H形桥塔主要的气弹现象,通过在H形塔柱双肢增加透风屏障可以有效地减小旋涡脱落,从而显著减小钢桥塔的涡激振幅。以上研究的钢桥塔均为典型的双柱式,与双柱式桥塔不同,“人”字弧线形钢桥塔在横桥向来流风作用下,桥塔自身绕流及塔柱之间的相互气动干扰均具有显著的三维流动特性。已有研究表明,塔柱截面形式对桥塔的气动稳定性有着重要的影响[6],因此针对形式新颖的“人”字弧线形钢桥塔进行气动选型及风致响应研究非常必要。
以世界第一座弧线形钢桥塔斜拉桥——南京长江三桥为工程背景,该桥桥塔采用“人”字弧线形布置,全高215m,塔柱断面为带切角的矩形(如图1所示)。该桥塔上部约180m采用钢结构,下部约35m采用混凝土结构,作为桥塔与基础之间的连接段。桥址区属北亚热带湿润季风气候,易受台风侵袭,风环境较为严峻。由于桥塔在主梁高度以上采用钢结构,整个结构质量轻、阻尼小,且整个桥塔较高,对风的作用较为敏感。钢桥塔在中国少见,对钢桥塔的风振性能缺乏经验,加之样式新颖,其抗风性能已成为设计的控制性因素。针对“人”字弧线形钢桥塔,为考虑其气动性能的三维特性,采用气弹模型风洞试验的方法,基于涡振性能对塔柱断面形状进行了气动选型,针对选定的断面形式,进一步开展了大缩尺比的气弹模型风洞试验,较全面地考查了该桥塔在中低风速下的涡激振动及在高风速下的驰振性能,对比了阻尼比对桥塔涡激振动振幅及驰振临界风速的影响。试验中选择最不利的裸塔状态(桥塔施工完成,尚无拉索连接)来开展研究,试验来流偏安全地采用均匀流。
1 桥塔动力特性
采用自主研发的桥梁结构科研分析软件BANSYS(Bridge ANalysis SYStem)[8]对该桥塔的自振特性进行了分析,采用空间梁单元建立有限元模型,桥塔顺桥向、横桥向及扭转振动的基频分别为0.199、0.913及1.702Hz,对应的振型如图2所示。桥塔顺桥向弯曲基频较其它阶频率明显偏小,对风的作用可能较为敏感,后续试验中需重点考查。
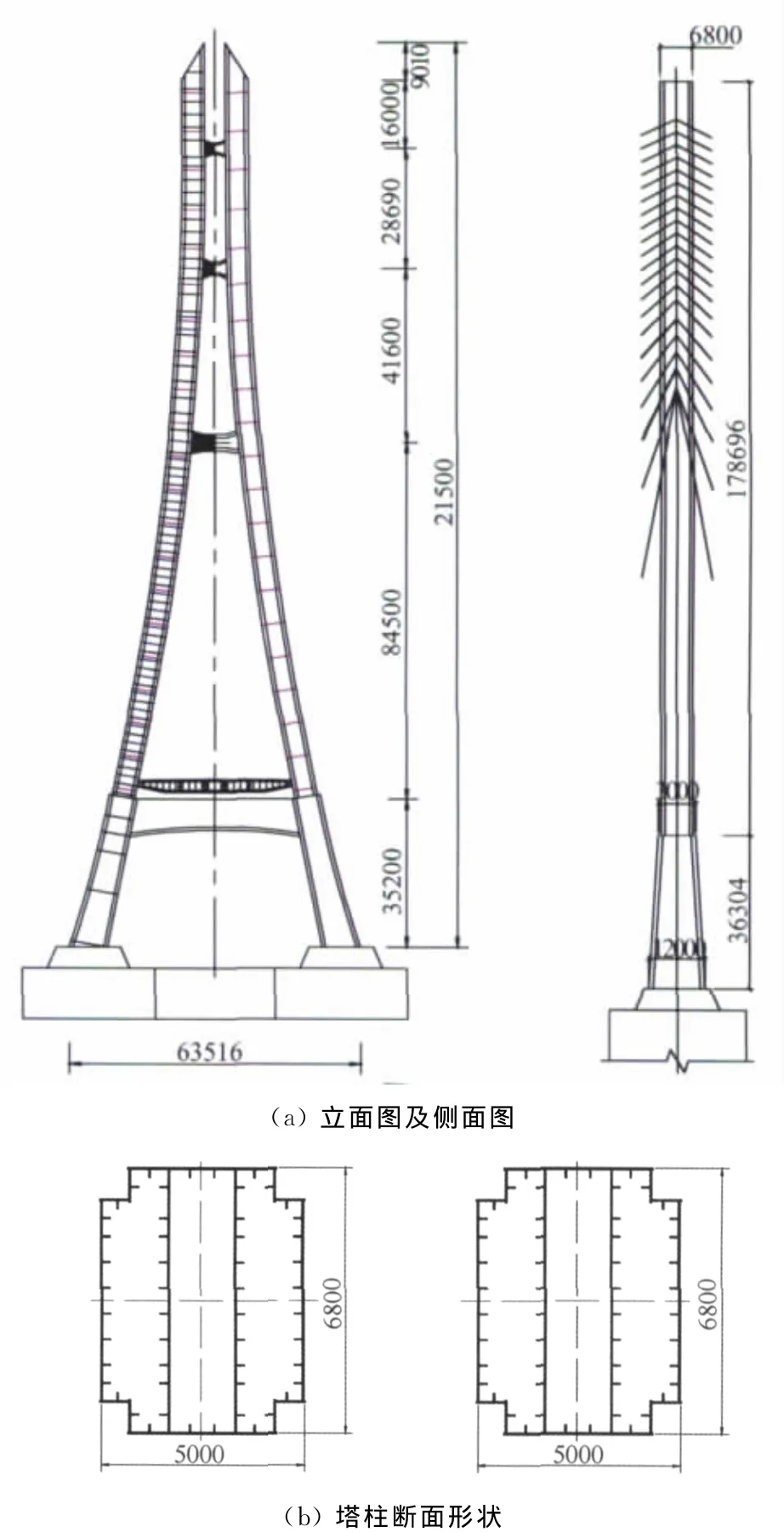
图1 桥塔总体布置及塔柱断面形状(单位:mm)Fig.1 General layout of pylon and cross-section shape of pylon pillar(dimensions are given in mm)
2 基于涡振性能的气动选型
涡激振动发生风速通常较低,出现频度较高,易使结构构件产生疲劳破坏或人感不适。涡激振动兼具自激振动和限幅振动双重特性,对结构的质量和阻尼较为敏感,当结构质量和阻尼均较小时,涡激共振振幅可能很大。该桥塔的塔柱截面为较钝化的带切角矩形断面,风作用下易在尾流区形成旋涡。此外,塔柱采用全钢结构,其质量和阻尼均相对较小,易发生涡激共振,常见风速下的涡振响应可能是钢桥塔的主要风致振动形式。为考虑桥塔的三维气动绕流,采用气弹模型,针对桥塔的涡振性能进行塔柱断面的气动选型。
2.1 气弹模型设计
气动弹性模型的几何参数、弹性参数、惯性参数需满足一致性条件要求,以保证模型结构静动力行为与原型相似。考虑到该桥桥塔高215m和西南交通大学XNJD-1风洞第一试验段的尺寸(3.6m宽×3.0m高),将模型的几何缩尺比定为CL=1/100。根据XNJD-1风洞第一试验段的风速范围,兼顾桥塔涡激振动试验的精度要求,模型设计时尽量增大顺桥向模态和横桥向模态对应的风速比,风速比取为CU=1/3,由相似条件可得频率比为Cf=33.3/1。对于带切角矩形断面,粘性参数条件并不显著影响其绕流的流态相似,加之目前缩尺模型风洞试验中难以满足粘性参数的一致性,该研究未严格模拟粘性参数相似。
桥塔的弯曲刚度由A3钢制成的芯梁提供,芯梁截面取为“T”形,以减小模型质量,使塔柱在满足弯曲刚度相似关系的同时兼顾模型的质量要求。桥塔气动外形由优质木材和航空层板制作,桥塔木外形分段安装,各段之间留有1mm的细缝,以消除梁段对模型刚度的影响。采用铅配重调整各段的质量,使之满足相似要求。为得到更显著的涡振现象采用较小的阻尼比,桥塔模型顺桥向基阶振动实测阻尼比为0.15%。
2.2 试验工况
针对结构的涡振性能,共进行了10种切角形式(如表1所示)的气动外形比选,针对每一种切角形式均进行了5种风向角β的振动特性测试。试验来流均为均匀流,5种β角分别为0°、22.5°、45°、67.5°、90°,模型β角为0°时表示顺桥向吹风,模型β角为90°时表示横桥向吹风(如图3所示)。

表1 切角对比试验工况(m)Table 1 Test cases of corner cut(m)
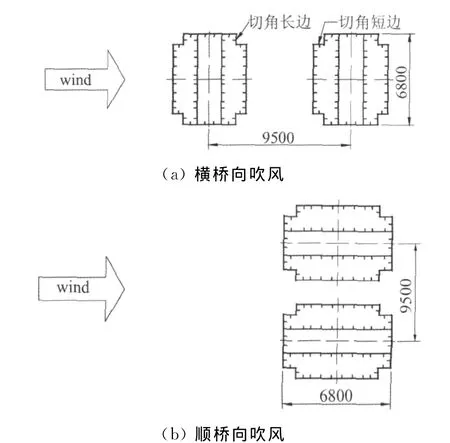
图3 试验风向示意(单位:mm)Fig.3 Schematic diagrams of wind direction(dimensions are given in mm)
2.3 结果分析
试验结果表明,各种切角断面在β=0°,22.5°,45°,67.5°,75°时均未出现明显的涡激振动,但当β=90°时各种切角断面均发生了较明显的顺桥向涡激振动。图4为β=90°(风向为横桥向)时十种切角断面塔顶顺桥向涡振振幅随风速变化情况。由图可知,切角长宽比增大时,涡振响应也有增大的趋势,当切角尺寸较小时出现了两个涡振区。涡振响应较小的切角方案为:0.8m×0.6m、0.6m×0.8m及0.6m× 0.6m。值得注意的是,0.6m×0.8m及0.6m×0.6m两种切角方案发生涡激振动对应的风速相对较低,更易发生涡激振动。
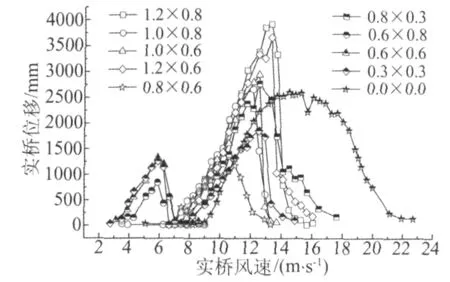
图4 塔顶顺桥向涡激振动响应Fig.4 Responses of longitudinal vortex-induced vibration at pylon top
3 切角形式细化及风向影响
在上述试验的基础上,进一步细化切角形式,在切角方案0.8m×0.6m的基础上,对比了0.9m×0.7m和0.8m×0.7m两种切角形式的涡振特性,并考查了当风向角β在90°附近较小变化时对三种切角断面塔柱涡振性能的影响。三种切角断面在不同β角情况下的塔顶顺桥向涡振振幅随风速变化情况如图5所示。由图可知,0.9m×0.7m切角方案对来流风向变化不敏感,另两种方案涡振响应随风向角变小而变小。总体而言,切角0.8m×0.7m的涡振响应最小,且适合工厂加工及现场拼接,故将0.8m×0.7m切角方案作为最优方案。
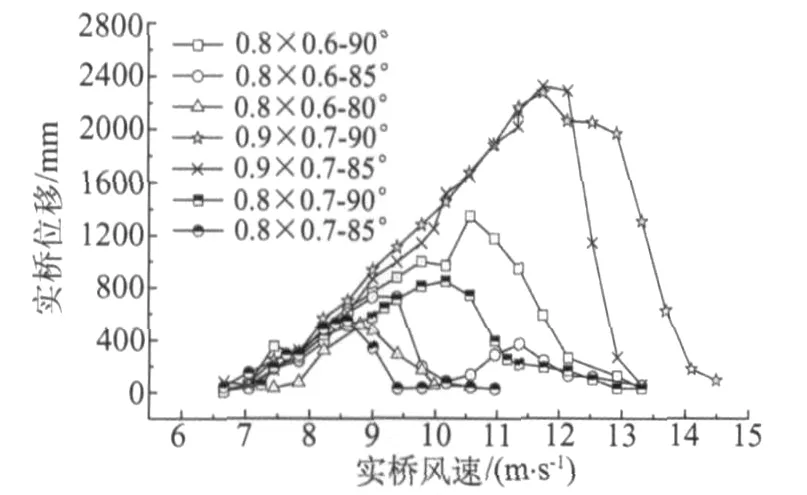
图5 不同风向时塔顶顺桥向涡激振动响应Fig.5 Responses of longitudinal vortex-induced vibration at pylon top for different yaw angles
4 大缩尺比气弹模型风洞试验验证
大缩尺比气弹模型试验的目的是对经优化比选后所确定桥塔方案的涡振性能和驰振性能进行检验,采用较大的几何缩尺比(1/70)重新设计制作了模型,兼顾涡振和驰振的试验要求,同时与后续抖振试验中的大气边界层模拟装置相匹配。为了提高测试精度,涡振试验中将基阶振动模态(顺桥向弯曲)的风速比提高为1/2。扭转驰振试验中,扭转模态对应的风速比为1/10.6。此外,还对比了该桥塔在两种阻尼比(0.15%,0.50%)情况下的涡激振动及驰振特性,分析了阻尼比的影响。

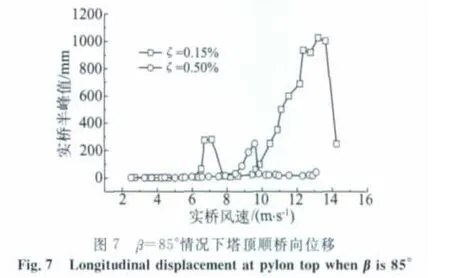
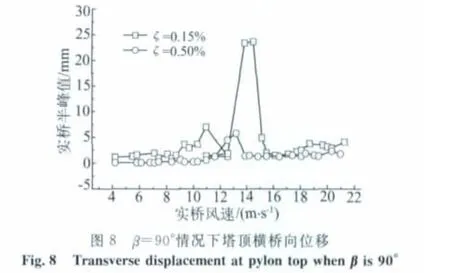
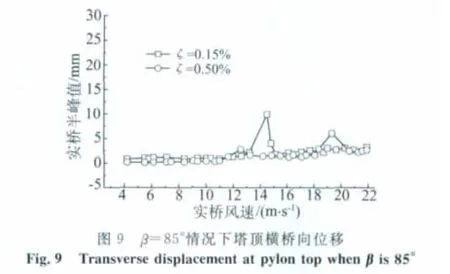
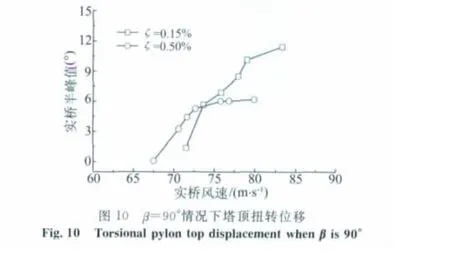

图11 β=85°情况下塔顶扭转位移Fig.11 Torsional displacement at pylon top whenβis 85°
均匀流条件下,采用不同阻尼比、不同β角共进行了10种工况的试验,受篇幅所限,仅给出β=90°和85°时桥塔位移响应随风速的变化[9],如图6~11所示,图中位移均指实桥塔顶高度处塔柱中心的位移半峰值。由图6、7可知,β=90°和85°时均发生了较明显的顺桥向涡激振动,两种阻尼比情况下β=90°时的响应较β=85°时的要大。当阻尼比为0.15%时顺桥向涡振有两个涡振区,而当阻尼比为0.50%时顺桥向涡振仅有一个涡振区,此外,两种β角情况下阻尼比为0.15%时的涡振响应均明显大于阻尼比为0.50%时的,这表明结构阻尼比对桥塔的涡振特性有较明显的影响。对比图6、7不同阻尼比下涡振发生风速可知,高阻尼情况下桥塔涡振发生风速略有提高,这可能是由于所研究的桥塔采用“人”字弧线形布置,结构沿高度形状变化较大,在同一风速下存在多种频率成分的涡脱,低阻尼时一旦存在与结构频率相同的涡脱成份,由于共振作用结构就会发生涡振,并出现频率锁定现象,而高阻尼情况下的涡激力必须大到一定程度时才可能发生涡振,通常涡激力随风速增加而增大,因此高阻尼情况下涡振发生风速可能会适当提高。对比图5和6中0.8m×0.7m切角方案的涡振特性可知,小缩尺比模型试验中由于试验风速过低未发现第一涡振区(起始风速约5m/s),大缩尺比模型试验中由于风速比的提高,较好地捕捉到了第一涡振区。不同缩尺比的桥塔模型第二涡振区对应的涡振振幅相当,涡振风速范围相近,略有差异。产生差异可能的原因包括:1)两种缩尺比模型在大振幅情况下结构真实阻尼可能存在一定差异;2)涡振的自激特性和锁定现象使涡振特性与加载路径有关,两次试验的加载方式不可能完全一致;3)桥塔是变截面结构,多种涡脱成份共存,且结构阻尼比非常小,结构响应对外界因素非常敏感,这增大了两种模型试验产生差异的可能性;4)尽管两模型涡振实桥风速范围相近,但由于风速比的差异,两模型试验风速差异较大,小缩尺比模型试验风速较低,风场的稳定性有所降低,这可能导致小缩尺比模型振幅变小;5)两种模型对应实桥振幅换算成试验振幅均较小,试验测试误差难以避免。由图8、9可知,桥塔横桥向涡振响应不明显,且涡振风速范围较窄。由图10、11可知,在实桥风速约为70m/s时结构出现了发散性的扭转驰振,其发振风速均高于该桥的驰振检验风速(51.5m/s)[9-10]。此外,由图可知,阻尼比对桥塔扭转驰振临界风速的影响较小。
5 结 论
通过对“人”字弧线形钢桥塔进行1/100的气动选型模型风洞试验和1/70的风致振动模型试验,可得出如下结论:
(1)在所研究的10种塔柱切角断面中,当β角在较大范围(0°~75°)变动时,各种切角断面均未出现明显的涡激振动和驰振。当来流为横桥向时(β= 90°)各种切角断面均发生了明显的顺桥向涡激振动,切角长宽比增大时,涡振响应也有增大的趋势。0.8m×0.7m切角断面的涡激振动响应相对最小,可作为推荐方案;
(2)对推荐切角断面(0.8m×0.7m),β为90°和85°时均发生了较明显的顺桥向涡激振动,且β为90°时的涡激振动响应要大于β为85°时;桥塔扭转驰振临界风速均较高,高于驰振检验风速;
(3)桥塔顺桥向涡激振动对结构的阻尼比较为敏感,随着阻尼比的增大,涡激振动振幅显著减小,涡振发生风速区间略有变化;阻尼比对桥塔扭转驰振临界风速影响有限。
[1] SIMIU E,SCANLAN R H.Wind effects on structures:fundamentals and applications to design[M].3rd ed.New York:John Wiley&Sons Inc.,1996.
[2] 卢桂臣,张红芬,杨詠晰,等.西堠门大桥初步设计钢箱梁断面气动选型[J].西南交通大学学报,2005,40(4):473-477.
[3] 刘小兵,刘志文,陈政清.双幅桥面主梁断面的气动选型[J].振动与冲击,2009,28(8):94-201.
[4] 马存明,李丽,廖海黎,等.特大跨钢桁梁悬索桥主梁气动力参数试验研究[J].四川建筑科学研究,2010,36(2):43-46.
[5] 王茜,王春生,俞欣,等.钢桥塔局部稳定试验与数值分析[J].长安大学学报(自然科学版),2008,28(5):67-72.
[6] TAKEUCHI T.Effects of geometrical shape on vortex-induced oscillations of bridge tower[J].Journal of Wind Engineering and Industrial Aerodynamics,1990,33(1-2):359-368.
[7] LAROSE G L,FALCO M,CIGADA A.Aeroelastic response of the towers for the proposed bridge over Stretto di Messina[J].Journal of Wind Engineering and Industrial Aerodynamics,1995,57(2-3):363-373.
[8] 李永乐.风-车-桥系统非线性空间耦合振动研究[D].西南交通大学,2003.
[9] 南京长江第三大桥桥塔抗风性能研究[R].西南交通大学风工程试验研究中心,2003.
[10]JTG/T D60-01-2004公路桥梁抗风设计规范[S].北京:人民交通出版社,2004.

