半柔壁喷管机构动力学仿真技术研究

聂旭涛，赖 欢，张艳辉

（中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

半柔壁喷管的喉道部分使用可转动和移动的固定型面喉道块，膨胀区使用柔性壁板。与全柔壁喷管相比，半柔壁喷管长度减少，降低了加工成本，并且能够实现风洞运行中马赫数的连续变化，风洞运行效率进一步提高［1］。半柔壁喷管的研究及应用在国外已逾半个世纪，而在国内却刚刚起步。深入研究半柔壁喷管的先进设计技术，对增强中国跨超声速风洞的试验效能具有重大现实意义。

半柔壁喷管是一个由多个刚体和柔性体组成的复杂多体系统，并受气动压力、作动点集中力以及自身重力等多种载荷作用。基于刚柔耦合动力学理论的动力学仿真软件ADAMS，为解决这类复杂动力学问题提供了一种有效的分析途径［2－4］。但是，ADAMS是采用模态柔性来表示柔性体弹性的，即模态向量和模态坐标的线性组合来表示弹性位移，对于存在柔壁大挠度变形以及螺钉联接接触等非线性问题的柔壁喷管来说，仿真计算结果会有较大误差，需要进行仿真模型改进。

联合ADAMS与PATRAN／NASTRAN软件，给出了半柔壁喷管机构动力学仿真的一般流程。针对柔壁大挠度变形以及螺钉联接接触等非线性问题，综合分段线性化、等效刚度等处理方法，建立了半柔壁喷管机构动力学仿真模型。为了验证该模型合理性，将其结果与NASTRAN软件非线性有限元计算、柔壁力学试验进行比较。最后，检查了柔壁型面与气动设计型面之间的吻合程度，并且分析了各个推杆驱动位移对试验段静压的影响关系。

1 半柔壁喷管机构动力学仿真流程

联合ADAMS和PATRAN／NASTRAN软件，实现半柔壁喷管机构动力学仿真，其一般流程为［5］：

（1）采用软件PATRAN建立柔壁的有限元模型，内容有：

① 选择单元划分网格；

② 定义连接点及其与相关节点间的多点约束关系 MPC（Multi－Points Constraint），用于柔壁与其它刚体或柔性体间的约束副连接，实现运动和力的传递；

③ 定义材料属性，如密度、弹性模量、泊松比等；

④ 提取载荷信息并生成.loads文件。

（2）运行NASTRAN，生成柔壁的模态中性文件 MNF（Modal Neutral File）。

（3）运用ADAMS软件mnfload工具，将.loads文件中的载荷信息添加到柔壁的模态中性文件MNF中。

（4）ADAMS／View环境下，建立半柔壁喷管机构动力学模型并仿真，内容有：

① 建立或导入刚体模型；

② 通过模态中性文件MNF导入柔壁模型；

③ 添加各个部件间的约束副关系；

④ 在各个部件上施加载荷或运动驱动。

（5）运行ADAMS／Solver，计算系统的运动微分方程。

（6）ADAMS／PostProcessor环境下，分析计算结果，提取柔壁上的载荷信息。

（7）根据载荷信息，利用软件NASTRAN有限元计算柔壁的非线性变形和结构强度。

（8）比较动力学仿真和非线性有限元计算的结果，若误差较大，则需改进柔壁的模态中性文件MNF，即转到步骤（1）重新开始。

2 柔壁大挠度变形模拟

ADAMS软件采用模态柔性来表示柔性体的弹性，属于线性方法。这对于存在大挠度变形的柔壁机构来说，仿真计算结果会有较大误差。因此，采取分段线性化的方法，即以推杆支点为界，将柔壁划分为5块子柔壁［5］。

基于前述仿真流程，建立半柔壁喷管机构动力学仿真模型，如图1所示，包括固块喉道、5块子柔壁和推杆组件1～6。推杆组件是电动推杆的简化模型，由套筒和推杆组成。子柔壁为柔性体，其余均为刚体。子柔壁模态中性文件MNF由PATRAN／NASTRAN创建，其中定义了2个连接点，并包含气动载荷信息。

图1 半柔壁喷管的组成Fig.1 Composition of semi－flexible nozzle

创建部件之间的约束副。子柔壁1前端与固块喉道、子柔壁5后端与大地（Ground）、相邻子柔壁之间为固定约束副；推杆组件1～6中套筒与大地、推杆组件2～6中推杆与固块喉道、子柔壁之间为旋转约束副；推杆组件1～6中套筒与推杆之间为移动约束副；第1根推杆与固块喉道之间为销－槽凸轮副。

在固块喉道、子柔壁上施加载荷，如气动压力、自身重力等。为各个推杆组件的移动副定义直线驱动速度，时间历程均分为加速、匀速和减速3个阶段，如图2所示。

图2 推杆的驱动速度曲线Fig.2 Drive velocity curve of handspike

设置求解器参数，运行ADAMS／Solver，得到半柔壁喷管机构动力学仿真结果，如图3，柔壁Von Mises应力最大为380.75MPa，出现在第3根推杆支点处。

图3 动力学仿真结果Fig.3 Result of dynamics simulation

从计算结果中，获取柔壁各个连接点的位移以及所受驱动力（力矩）。根据这些驱动力（力矩）信息，运用NASTRAN软件对柔壁部件进行非线性有限元分析，并将连接点的位移结果与动力学仿真结果作比较，如表1所示。其中，子柔壁5右端连接点与大地固定连接，位移为0mm，故不予比较。

表1 连接点位移结果的比较Table 1 Comparison of displacement results of joints

由表1可知，柔壁经过分段线性化后，位移误差最大只有16.2%，仅0.006mm的误差。因此，该半柔壁喷管机构动力学仿真模型能够模拟柔壁大挠度变形运动。

3 螺钉联接接触模拟

实际结构中，子柔壁5后端与后法兰之间采用螺钉联接，如图4所示。螺钉联接处存在多个接触面，零部件之间往往存在滑动、分离、弹性变形等多种现象，属于非线性范畴，机理十分复杂。如果采用固定约束副，柔壁在联接处会过约束，结构应力较大；如果采用旋转约束副，柔壁在联接处会欠约束，结构应力较小。如何模拟螺钉联接的接触非线性，是一个比较棘手的问题。

图4 柔壁与后法兰的螺钉联接Fig.4 Bolts link of flexible wall and back flange

借鉴国内外在机械结构结合部建模的经验，采用等效刚度法，即子柔壁5后端与大地之间用两件伸缩弹簧和一件扭转弹簧联接，如图5所示。

图5 等效刚度模型Fig.5 Equivalent stiffness model

伸缩弹簧包括X向弹簧、Y向弹簧，扭转弹簧为Z向扭簧。根据静载荷下梁杆的变位计算公式，可以得到弹簧的刚度公式为

式中，kx为X 向弹簧的刚度，ky为Y向弹簧的刚度，kz为Z向扭簧的刚度，E为螺钉材料的弹性模量，A为螺钉截面面积，l为螺钉长度，n为螺钉个数，G为螺钉材料的剪切模量，I为螺钉截面的轴惯性矩。

4 柔壁力学试验

柔壁力学试验目的是：以柔壁的结构应力为研究对象，通过比较动力学仿真与实际测量的结果，验证半柔壁喷管机构动力学模型的合理性。为测得柔壁的结构应力，需在柔壁上装贴5片单向应变片，见图6。柔壁与固块喉道联接处为测点1，推杆3（柔壁第1根推杆）支点处为测点2，推杆4、6支点处为测点3、4，柔壁与后法兰联接处为测点5。

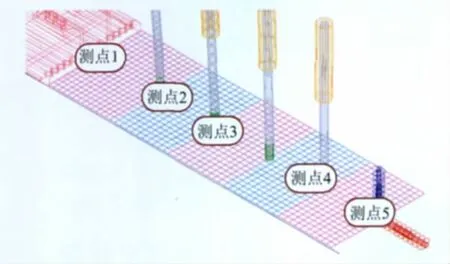
图6 柔壁应力测量位置Fig.6 Position of stress measure on flexible wall

综合分段线性化及等效刚度法，采用ADAMS软件建立半柔壁喷管机构动力学仿真模型。设置各个推杆组件的直线驱动速度。设置求解器参数，运行ADAMS／Solver，得到柔壁各测点处应力随时间变化曲线，如图7。由图可知，柔壁最终成型时，测点1～5处的X 向主应力值分别是：71.1、302.1、228.3、88.5和74.9MPa。

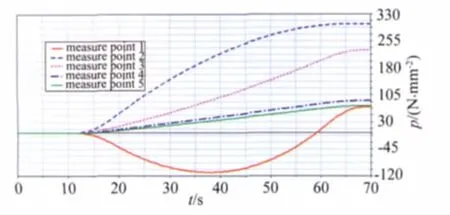
图7 柔壁测点应力曲线Fig.7 Stress curves of measure points on flexible wall

按照上述推杆驱动速度，控制半柔壁喷管机构的实际运动，应变片测量得到柔壁测点处应力变化历程曲线，如图8。可知，柔壁最终成型时，测点1～5处的X 向主应力值分别是：62.2、262.3、205.1、70.0和70.2MPa。

图8 柔壁应力实际测量结果Fig.8 Actual measure results of flexible wall stress

比较仿真计算与试验测量结果，可以看到：

（1）以柔壁结构应力为对象，半柔壁喷管机构动力学仿真计算与试验测量的结果基本一致，特别是在应力值随时间变化过程方面。

（2）仿真与试验结果存在误差，主要原因是：

①喷管结构多为焊接件，加工存在误差；

② 应变片装贴位置存在误差；

③ 柔壁有限元模型铰链联接处为MPC约束，与实际结构相比，刚度较强，设计偏安全。

（3）测点5处应力仿真误差不大，说明等效刚度法模拟螺钉联接的接触非线性是合理可行的。

5 柔壁与气动曲线的吻合度检查

柔壁挠性曲线的曲率分布图是推杆间的一系列直线，将其重叠在理论气动型面曲线的曲率图上，计算推杆间代表曲率的直线段和理论气动曲线曲率的图线之间包围的面积，即为斜率误差，作为曲率吻合误差的度量。同时，斜率误差与试验段静压变化相联系，也可得到相应的马赫数变化。采用这种方法估计试验段流场的不均匀性，常常是合理的，因为最大误差常常发生在终止段［6］。

图9、10分别显示了气动设计型面与喷管结构型面以及气动型面曲率与柔壁型面曲率。

图9 气动与结构型面曲线Fig.9 Shape curves of airstream and structure

图10 气动与结构型面曲率Fig.10 Shape curvature of airstream and structure

根据图10计算两个曲率曲线之间包围的面积Δθ＝0.0052rad。按照文献［6］给出的公式计算试验段静压变化为

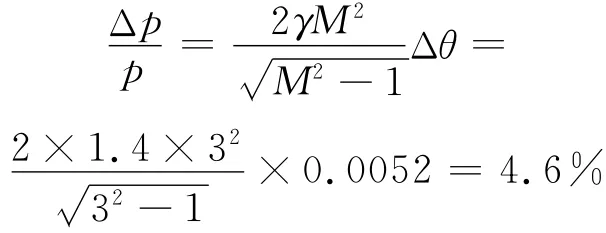
调整柔壁特征点P处的推杆（即推杆3）驱动速度，使得柔壁的最大X向主应力达到600MPa左右，此时推杆3驱动位移变化量为1.805mm。按照相同位移变化量，分别调整推杆4、5和6驱动速度（单独调整每根推杆，其他的保持不变）。基于半柔壁喷管机构动力学模型，分别计算上述4种情况，得到相应的柔壁型面以及曲率曲线，分别如图11、12所示。

根据图12计算柔壁的结构型面曲率曲线与气动型面曲率曲线之间的包围面积，4种情况分别是：0.030、0.035、0.034和0.027rad。

按照文献［6］给出的公式计算试验段静压变化，4种情况分别为：26.4%、31.3%、29.9%和23.7%。因此，推杆4的驱动位移对试验段静压变化影响最大，约为14.79%／mm。

图11 调整后的柔壁型面曲线Fig.11 Shape curves of flexible wall after adjusting

图12 调整后的柔壁型面曲率Fig.12 Shape curvature of flexible wall after adjusting

6 结束语

半柔壁喷管的关键技术指标是柔壁的结构强度及型面吻合度。基于刚柔耦合动力学理论，联合ADAMS和PATRAN／NASTRAN软件，同时采用分段线性化与等效刚度等处理方法，计入柔壁变形和螺钉联接接触等非线性环节，建立了半柔壁喷管机构动力学仿真模型。将仿真结果与NASTRAN非线性有限元计算以及柔壁力学试验结果相比较，表明该动力学仿真模型能够达到较高的准确度。最后检查了柔壁型面与气动曲线之间的吻合度，并在此基础上进一步计算分析了推杆的驱动位移对试验段静压变化影响关系，可为喷管动调提供必要的依据。

所研究并实现的半柔壁喷管机构动力学仿真技术，能够较为准确地仿真模拟喷管型面的成型运动，以及有效地计算分析喷管柔壁的结构强度，这对半柔壁喷管的结构设计与研制具有重要理论指导价值。

［1］ 刘政崇.高低速风洞气动与结构设计［M］.北京：国防工业出版社，2003.

［2］ LINKINS P W.Finite element appendage equations for hybrid coordinate dynamics analysis［J］.Journal of Solid＆Structures，1972，8：709－731.

［3］ HECKMANN Andreas，ARNOLD Martin，VACULIN Ondrej.Modal multifield approach for an extended flexible body description in multibody dynamics［J］.Multibody System Dynamics，2005，13（3）：299－322.

［4］ 高立新，胡延平，吴红艳.基于ADAMS的刚柔耦合汽车悬架性能分析［J］.合肥工业大学学报（自然科学版），2009，32（6）：814－817.

［5］ 聂旭涛，郭隆德，刘伯林.基于ADAMS风洞柔壁喷管动力学仿真分析［J］.实验流体力学，25（2）：73－76.

［6］ RIISE H N.Flexible plate nozzle design for two－dimensional supersonic wind tunnels［R］.Jet Propulsion Laboratory Report No.20－74，1954.