套筒式张线天平的研制

张 平，赵长辉，刘博宇

（中国航空工业空气动力研究院，沈阳 110034）

0 引 言

在高速风洞中，全机测力试验主要采用尾支撑及腹部支撑。由于空气动力学的快速发展，出现了特种布局形式的飞机，单纯的尾支撑及腹支撑已不能满足风洞试验的需要［1－2］。近年来，国内风洞发展了一种新型的全机测力模型支撑——张线支撑［3－4］。该支撑具有刚度大、干扰小、适应性强等优点，特别适用于带有大船尾角后体等特种布局飞机的全机测力试验。由于中航气动院FL－2高速风洞试验段尺寸的限制，张线天平的可用空间较小。因此，在张线支撑系统中，张线天平的研制非常关键。为此，笔者设计了一种套筒结构形式的天平，较好地保证了天平的整体刚度，满足了民机张线测力试验的特殊要求。

为满足民机张线测力试验的特殊要求，中航气动院FL－2风洞研制了一套高速民机张线支撑系统，其张线与水平面的夹角达到64.5°，迎角变化范围为±18°。此次试验所用标准模型是在GBM－01标模的基础上改造而成，马赫数范围为0.5～0.9，试验迎角范围为－4°～8°。

1 天平设计

1.1 天平方案选择

根据民机张线测力试验的特殊要求，天平在进行方案设计时选用了两种形式：一种为套筒结构形式，另一种为常规悬臂梁环状结构形式［5］。

套筒结构形式的张线天平具有以下特点：

（1）由于天平元件主要采用拉压变形形式，因此天平变形较小，天平刚度较强。

（2）天平内杆两端与8根张线拉杆相连接，天平外套筒与模型内腔相连结，因此天平的连接较牢固。

（3）由于天平的外套筒和内杆通过焊接相连接，因此对天平的加工工艺及焊接工艺要求较高。天平的加工成本较高。

常规悬臂梁环状结构形式的张线天平具有以下特点：

（1）由于天平元件主要采用弯曲变形形式，因此天平变形较大，天平刚度相对较弱。

（2）天平一端通过天平内杆与8根张线拉杆相连接，天平另一端与模型内腔相连结。由于天平轴向尺寸的限制，两端的连接尺寸较短。因此天平的连接相对较弱。

（3）由于天平采用常规的元件形式，因此天平的加工成本较低。

张线支撑的模型在试验过程中，当给定迎角时，要求其姿态角的变化尽量小，而模型姿态角的变化主要来自天平受载产生的弹性变形。常规悬臂梁式天平由于结构形式的局限性，必将产生相对较大的弹性变形，这与民机张线测力试验的要求相矛盾。因此，采用套筒结构形式的天平为好。在理想情况下，可以认为纵向载荷在天平元件处产生拉压变形，而拉压变形所形成的线位移较小，这样就满足了模型姿态角变化尽量小的要求，既可以节省模型内部空间又能承担更大的载荷。同时，张线天平与支撑机构及模型内腔连接面积的相对增加，也有利于天平可靠连接。从理论计算上，套筒结构形式的天平各分量的应变输出也较合理。

1.2 天平结构设计

由于中航气动院FL－2高速风洞实验段尺寸的限制，张线天平的结构尺寸相对较小，但天平所受载荷较大。因此，天平设计必须克服尺寸小但载荷较大的矛盾，如何有效保证天平外套筒和内杆的刚度及其连接处的刚度，将是张线天平设计成败的关键因素，天平设计难度较大。

图1 天平实物图Fig.1 The photo of balance

以前曾经结合某工程设计了一台张线天平如图1所示。由于模型尺寸限制，该天平采用套筒变截面结构形式，外套筒和内杆采用电子束焊接，中间锥度部分连接模型，两端通过球铰与8根张线连接，法向力、俯仰力矩、滚转力矩、横向力、偏航力矩均采用拉压梁式结构（其中轴向力为“S”形变形结构），共12片梁，12片梁的支撑端为悬臂梁，天平内杆较细，张线连接件安装在天平内杆两端，所以天平内杆实际是两端铰支的。经校准发现该天平存在诸多问题：一是天平各分量回零较差；二是天平各分量之间干扰较大；三是天平各分量灵敏度较低，特别是法向力及横向力输出较小。以上3种原因造成天平精度较低，无法用于风洞试验。分析其原因，此天平主要有以下几点不足，造成灵敏度降低，干扰增大：（1）天平元件在天平外套上，这就要求天平外套要有一定的厚度，而天平外套元件处的最小直径为φ38mm，这就使此处天平内杆的直径只有φ24mm，造成天平内杆刚度较弱，天平内杆在载荷作用下产生较大变形，带动天平元件变形；（2）天平受载后天平铰接端处存在摩擦力，使内杆变形后不能完全复原；（3）元件支撑梁为悬臂梁且刚度较弱，变形后造成拉压元件产生弯曲变形，将拉压变形抵消；（4）外套筒和内杆是在端部焊接在一起的，焊接工艺性较差，若焊接有缺陷会造成天平不回零，但这种缺陷无法检测。造成天平不回零的原因可能还有张线连接球摩擦力较大，张线连接位置离天平元件较近等原因。

结合民机张线测力试验设计了一台全新的张线天平如图2所示。考虑到天平整体刚度的要求，在模型设计时，经反复协调，将布置天平的结构内腔加到最大允许范围。而有些因素如实验段张线机构已经无法改变，因此只能在天平元件结构形式上寻求突破。该天平采用套筒等截面结构形式，外套筒和内杆采用电子束焊接，中间锥度部分连接模型，两端通过球铰与8根张线连接，在天平结构设计上，通过对原张线天平精度低的分析，借鉴浮框式天平的特点做了如下创新：（1）将天平元件都布置在外套筒上，外套筒元件处的直径设计为φ58mm，法向力、俯仰力矩、滚转力矩、横向力、偏航力矩元件布置在两端，共4片梁，其中法向力、俯仰力矩和滚转力矩为拉压变形，横向力和偏航力矩为“S”形变形，元件处支撑部分由受弯曲变形改为受拉压变形且刚度较强，同时也减小了切削量，轴向力元件布置在外套筒中间，其为弯曲变形，这样布置大大提高了外套筒的整体刚度；（2）天平内杆是直径为φ44mm的实芯粗轴，其上没有布置天平元件，这样就大大提高了内杆的整体刚度；（3）加大了天平外套元件之间的距离，将其尽可能布在远离天平与模型连接处及天平与8根张线拉杆连接处，以减小天平与模型连接处残余应力对天平外套元件的影响，同时也减小了张线连接球处摩擦力对天平可能造成的影响；（4）外套筒和内杆通过楔块在楔块端部焊接在一起，焊接工艺性好，此种焊接方法容易保证焊接质量；（5）天平外套与模型采用1∶50锥度连接，此连接方式可靠。通过正反楔子拉紧及退出连接。

图2 天平结构图Fig.2 3Ddiagram of wired balance

在完成天平结构设计后，通过有限元分析对天平各分量进行了应变计算，在法向力作用下，天平元件侧面中部平均应变约为438×10－6，实测值为460×10－6（见图3）；在俯仰力矩作用下，天平元件侧面中部平均应变约为240×10－6，实测值为260×10－6（见图4），从中可以看出计算结果与天平实际输出较吻合。

图3 法向力作用下天平应变云图Fig.3 Balance strain contour applied normal force

图4 俯仰力矩作用下天平应变云图Fig.4 Balance strain contour applied pitching moment

1.3 天平元件计算

天平在法向力作用下，元件应变按拉压变形计算。

天平在俯仰力矩作用下，元件应变按拉压变形计算。

天平在滚转力矩作用下，元件应变按拉压变形计算。

天平在轴向力作用下，元件应变按弯曲变形计算。

天平在横向力作用下，元件应变按“S”形变形计算。

天平在偏航力矩作用下，元件应变按“S”形变形及扭转变形计算。

天平各分量具体计算结果见表1。

表1 天平设计参数与静校精准度Table 1 Design parameters and the calibration precision and accuracyof balance

天平材料选用F141，强度校核时，分别对天平元件处及天平最小直径处的截面进行了详细计算，其结果均在［σ许］范围以内，天平强度满足要求。

天平结构示意图如图5所示。

2 天平静校结果

张线天平外形尺寸虽然较大，但天平元件处应变计的数量较集中且粘贴应变计所用空间尺寸较小，因此天平供桥电压不宜太高。天平各分量均采用4片应变计组桥，供桥电压为5V，各分量的最大输出见表1。

张线天平完成应变计粘贴后，在BACS1500校正台上完成了地轴单元校准。校准时，将张线天平内杆通过8根张线固定在校正台支架上，天平外套安置于加载头内。

天平各分量的零点漂移均在各分量最大输出的0.1%以内，综合校准精度优于0.06%，综合校准准度优于0.5%，其结果见表1。

3 风洞试验结果

下面是马赫数为0.6时，采用张线天平进行3次重复性试验的数据。从试验结果看，天平及张线支撑系统刚度好，法向力系数、俯仰力矩系数试验数据的重复性较好。与国内GBM－01标模统一试验数据比较，趋势一致，量值接近。因此，该天平的测量结果是可信的。天平测力曲线见图6。

图5 天平结构示意图Fig.5 Sketch of balance structure

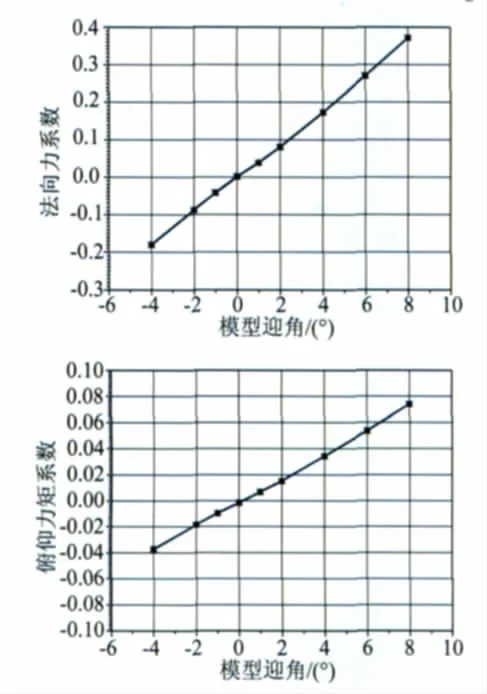
图6 天平测力曲线Fig.6 Balance measurement curve

4 结 论

（1）张线天平是中航气动院第一台通过静校检验合格并用于高速试验的套筒式天平。它具有结构合理，灵敏度高，性能稳定，精准度高等特点。天平的研制是成功的；

（2）张线天平连接可靠，天平整体刚度较常规天平有较大提高，为民机张线测力试验提供了保障；

（3）张线天平的成败关键在于把好焊接工艺这一关，实践证明国内的焊接工艺已达到较高水平。此天平成功研制为国内同类天平设计提供了一定的借鉴。

［1］ 恽起麟.风洞实验［M］.北京：国防工业出版社，2000.

［2］ 范洁川主编.风洞试验手册［M］.北京：航空工业出版社，2002.

［3］ 王世红，杨希明.FL－2风洞民机实验技术研究［J］.航空科学技术，2005，（6）：30－32.

［4］ 卞於中，李祥瑞，李立，等.低速闭口风洞模型张线支撑及内天平测量系统的研制［J］.流体力学实验与测量，1999，13（3）：85－90.

［5］ 贺德馨主编.风洞天平［M］.北京：国防工业出版社，2001.