适于多分支输电线路的故障支路判别算法

顾 伟，王 波

（浙江宁波电业局，宁波 315000）

输电线路承担着传送电能的重要任务，其故障的发生将直接威胁到电力系统的安全运行。准确的故障测距对于加快排除线路故障和尽快恢复供电具有十分重要的意义［1，2］。

国内外学者对于输电线路故障测距方法研究已进行了数十年，提出了大量的故障测距方法，如行波法、阻抗法等，也有专家将人工神经网络、小波原理等智能原理应用到故障测距中。而其中的阻抗法由于测量装置要求简单、算法实用而广受关注。阻抗法一般可分为：单端和双端测距算法，单端定位算法［3，4］由于仅采用单侧电气量数据，导致故障信息量不足，测距精度始终要受系统运行方式和过渡电阻的影响。而双端测距算法［5～7］能充分利用线路双端故障信息，因而可以取得很高的测距精度；尤其是当前PMU（phase measurement unit，相量测量单元）装置的研发和同步相量测量技术的发展，使同一时标下的双端故障测距计算成为可能，从而大大提高实际应用测距精度。

近年来，随着社会对电力的需求不断增长，而区域输电网络发展的相对滞后，导致小型发电厂或负载通过相对较短的线路连入高压输电线路的情况越来越多。虽然目前线路双端系统的故障测距算法比较成熟，但由于结构上的特殊性，很难将双端测距原理直接用于上述情况。而解决分支线路故障测距的关键是判断故障所在的支路，一旦故障支路已知即可通过非故障支路的等效合并，将其转化为传统的双端测距问题。因此文献［8～12］等提出了适用于三端或多端线路的故障分支判定算法，但这些方法都是基于各端的电气量，即假设每条线路母线均装设PMU。为减少PMU的配置，文献［13，14］提出一种仅利用线路两端PMU，实现对单分支输电线路故障支路判定，但该方法只适用于一条分支的情况。

基于上述研究，本文提出一种适用于任意多分支输电线路的故障支路判别算法。该算法将仅利用线路两端的PMU测量值，建立通用性的故障支路判定指标，通过迭代似的比较方法，准确判别故障所在支路，进而可转化为传统双端测距问题。本文将首先分析传输线路出现单分支的情况，进而延伸到两分支、任意多分支的情况。

1 故障分支判别算法

1.1 传统双端测距原理

如图1所示的三相对称传输线路，线路两端S、R处装设PMU（下文均如此）。当该线路上发生短路故障后，由线路两端的正序电压、电流分量（VS1，IS1）、（VR1，IR1），根据双端测距原理［4］可计算得故障点F的准确位置为

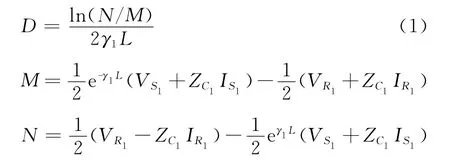
式中：D为故障点F到线路R端占总长度L的百分比；γ1、ZC1分别为该传输线路的正序传播系数、特性阻抗。

上述公式是由线路的分布参数模型求解所得。由电力系统分析原理可知，当架空线路长度小于300 km时或电缆线路短于100 km时，其线路模型亦采用集中参数模型代替。

图1 无分支的传输线路Fig.1 Transmission line without tapped leg

1.2 单分支判别原理

当输电线路出现一条分支时，如图2所示，其中线路BT为分支。由于该分支的出现，故障有可能发生该分支系统的任意区域，包括支路SB、BR及分支BT；在故障分支不明确的前提下，传统的双端测距算法无法直接应用。

图2 单分支传输线路Fig.2 Transmission line with only tapped leg

由线路两端的故障附加正序分量（VS，sup，IS，sup）、（VR，sup，IR，sup）根据双端测距式（1）进行计算可得故障位置D，由于实际分支的存在，显然此时的计算值不是正确的故障位置D1，但该计算值通过与分支点所在位置Dtap比较，可以确定故障所在的分支线路，具体故障线段判断方法如下［14］：

（1）当Re（D）＜Dtap时，表明该短路故障发生在支路BT（不包括节点B）；

（2）当Re（D）＝Dtap时，表明该短路故障发生在分支BT（包括节点B，下文所述的分支线路均包括该支节点）；

（3）当Re（D）＞Dtap时，表明该短路故障发生在支路SB（不包括节点B）。

其中Re（D）代表取D的实数部分，因为实际计算所得的D可能是复数。

理论上该判据成立，但由于计算、仿真误差的存在，在分支线路上发生故障时，计算值Re（D）不可能完全为零，因此需设置一定的裕度值ΔD（具体视算例而定），满足Re（D）≤｜Dtap±ΔD｜即可认为Re（D）＝Dtap。

1.3 两分支判别原理

当传输线路出现两条分支线路时，如图3所示。其中B1T1、B2T2为分支线路。

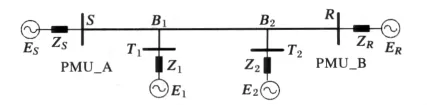
图3 两分支传输线路Fig.3 Transmission line with two tapped legs

当该分支系统中发生短路故障时，由线性叠加原理可知，故障电力网络可分解为故障前正常状态网络与故障附加网络；同时采用对称分量法，可将故障附加网络分解为正序网、负序网和零序网。假设图3线路B2R上点F处发生故障时，按上述分解原理［16］，可建立如图4所示的故障附加分量正序网，该网络为仅故障点存在电流源。

图4 故障附加分量正序网Fig.4 Positive sequence network of additional fault component

如图4所示，Z11、Z21分别为两分支T1、T2母线端的已知等效正序阻抗，D1、Dtap1、Dtap2分别为故障点F、分支接点B1、分支接点B2到R端的距离占线路总长的百分比，L1、L2、L3分别为支路SB1、B1B2、B2R的长度。

线路SR两端的故障附加正序电压、电流分量（VS，sup，IS，sup）、（VS，sup，IR，sup）计算式为

式中：VS，post、VR，post、IR，post、IS，post为端故障后正序分量；VS，pre、VR，pre、IS，pre、IR，pre为故障前正序分量。

由于传输线路中两条分支的存在，故障可能的发生区域进一步复杂化，包括线路分支SB1、B1B2、B2R及分支B1T1、B2T2。

由第1.1节可知，对于无分支输电线路，由双端同步数据（VS，sup，IS，sup）、（VR，sup，IR，sup）计算的故障指标D即为准确的故障位置；由第1.2节可知，对于单分支输电线路，此时计算的故障位置指标D反映的是故障所在的线段；而对于两分支的情况，显然D既不是正确的故障位置，也无法直接反映故障线段。为此下面将分析故障发生在两分支线路不同区域时，计算指标D的特性。

情况1 当故障发生在支路B2R或分支B2T2时，如图4所示实际故障发生在点F，则满足故障位置为

根据KVL原理，此时线路两端S、R的电压值VS，sup、VR，sup满足表达式（采用集中参数模型）

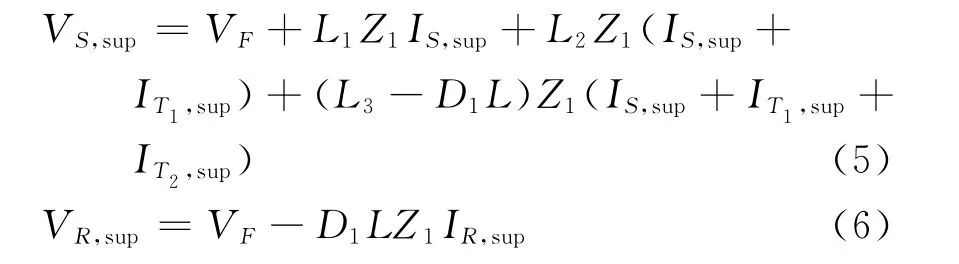
式中：IT1，sup、IT2，sup为两分支路的故障附加正序电流值；Z1为该线路的单位正序阻抗；VF为故障点电压值；L为线路SR的总长度。

由式（5）与式（6）相减可得

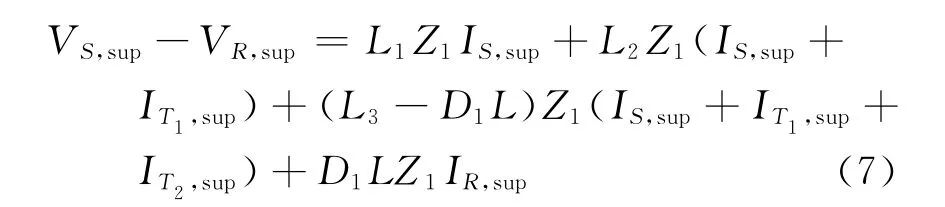
若根据传统的双端测距原理，直接计算得故障位置D，显然该计算值不是准确的故障点位置，以图1所示，此时线路两端S、R的电压值VS，sup、VR，sup应满足表达式

同理由式（8）、式（9）相减可得

结合上述两种情况，整理式（7）、式（10），从而可建立实际故障位置D1与计算故障指标D的等式关系为

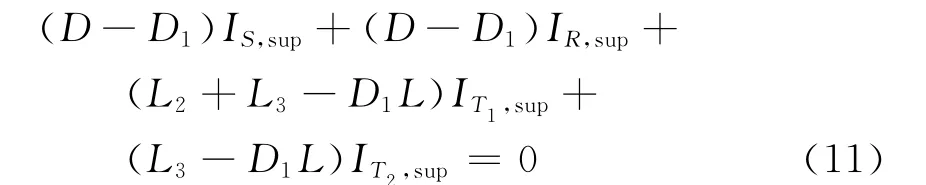
由于计算的D有可能为虚数，为此对式（11）两边均取实部幅值，可得

式中：k1＝（L2＋L3－D1L）／L；k2＝（L3－D1L）／L。

由式（4）可知，此时k1＞0，k2≥0。进一步解析式（12），其等效为

假设该输电线路系统的所有电源端阻抗包括ZS1、ZR1、ZT11、ZT21均是高感抗（即RX），则IT1，sup、IT2，sup分别与IS，sup、IR，sup之间的相角度数差均小于90°。事实上，实际阻抗亦满足此条件，对于双分支情况只需R＜X即能得出上述结论。由此可得

进而有

即此时计算的故障指标D满足

情况2 当故障发生在支路B1B2时，即实际故障点位置D1满足

同理情况1方法可推得关系式

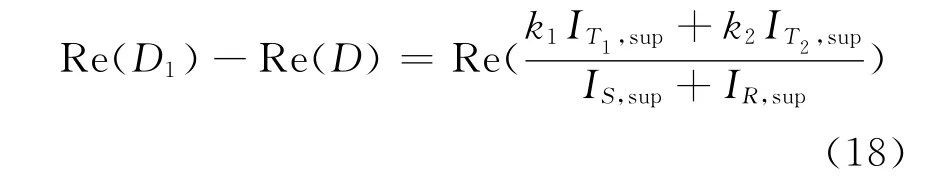
式中：k1＝L2＋L3－D1L＞0；k2＝L3－D1L＜0。

由于此时k1、k2的正负异号，导致无法确保计算值正负的一致性，即无法确定Re（D）与Re（Dtap1）、Re（Dtap2）之间的大小关系；此时计算的故障指标D可能分布在线路各个分支区间。

情况3 当故障发生在支路SB1或分支B1T1时，同理按照情况1的证明方法，此时计算的故障指标D满足

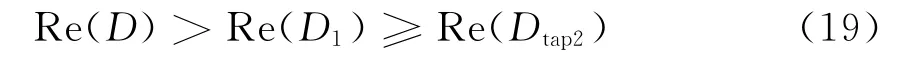
综上所述，通过与分支节点位置Dtap1、Dtap2比较，计算指标D能反映出故障所在的区域范围，排除不可能的故障线段，可得故障区域判据如下。

（1）当Re（D）＜Dtap1时，表明故障仅可能发生在区域B1R（包含支路B1B2、B1R和分支B2T2）。

（2）当Dtap1≤Re（D）≤Dtap2时，故障仅可能发生在支路B1B2。

（3）当Re（D）＞Dtap2时，故障仅可能发生在区域SB2（包含支路SB1、B1B2和分支B1T1）。

根据上述方法，由计算的故障指标D可将故障范围初步锁定，缩小至区域B1R或区域SB2或支路B1B2。若故障发生在区域B1R，将非故障支路进行等效合并，即转化为以B2T2为分支的单分支线路情况；若故障发生在区域SB2，同理可转化为以B1T1为分支的单分支线路；若故障发生在支路B1B2时，即已直接实现了故障支路的判断。

因此通过本节故障区域的初步判断，可将两分支线路问题转化为第1.2节的单分支问题或直接实现故障支路的准确判断。

对于双分支问题，可通过缩小可能故障区域范围，把双分支线路转化为单分支测距问题，进而实现故障分支的有效判断。具体流程如图5所示。

图5 故障分支判别流程Fig.5 Discrimination procedure of fault location

1.4 多分支判别原理

如图6所示，当传输线路出现n条分支时（n≥3），同理可建立如图7所示的故障附加分量正序网。

图6 传输线路出现多分支的情况Fig.6 Transimission line tapped with multi－legs

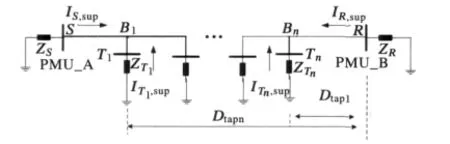
图7 故障附加分量正序网Fig.7 Positive sequence network of additional fault component

将上图中节点B1、Bn间的分支线路作为一整体，类同于两分支情况，同样可由线路S、R双端的故障附加正序电压、电流数据计算故障指标D，此时该计算指标的特性分析如下。

情况1 故障发生在支路BnR、分支BnTn时，若D1为实际故障点位置，则满足D1≤Dtap1；假设D为计算的故障指标值。由KVL，类似与式（12）可推导得

Re（D1）－Re（D）＝

其中k1，k2，…，kn均为非零常数，且若所有电源端阻抗均为高感抗（即RX），即IT1，sup，IT2，sup，…，ITn，sup与IS，sup、IR，sup的相角度数差均小于90°，则可得

情况2 故障发生在节点B1、Bn间的所有支路时，同理可推导得

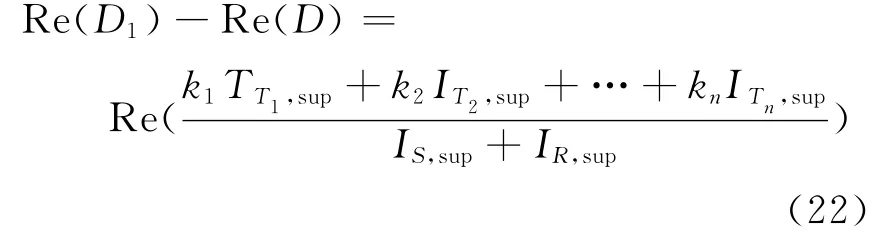
其中k1，k2，…，kn将有正有负，因此无法确定Re（D）与Re（D1）间的大小关系

情况3 故障发生在支路SB1、分支B1T1时，完全同（1）证明可得

综上所述，通过与分支节点Dtap1、Dtapn比较可得故障区域判据如下。

（1）当Re（D）＜Dtap1时：故障仅可能发生在除支路SB1、分支B1T1外的所有区域；由此通过将非故障支路SB1、分支B1T1进行合并，从而转化为（n－1）条分支情况。

（2）当Dtap1≤Re（D）≤Dtapn时：故障发生在除支路SB1、BnR及分支B1T1、BnTn外的所有区域；由此通过将非故障支路SB1、BnR及分支B1T1、BnTn进行合并，从而转化为（n－2）条分支情况。

（3）当Re（D）＞Dtapn时：故障发生在除支路BnR、分支BnTn外的所有区域；由此通过将非故障支路BnR、分支BnTn进行合并，从而转化为（n－1）条分支情况。

由此可见，故障计算式D给出了通用性的故障区域判别指标，通过其与分支节点位置的比较，排除非故障支路，进而采用迭代式的判断方法，将故障区域不断缩小，最终可转化两分支情况。

2 算例仿真

为了验证本文算法的有效性和正确性，本节将采用PSCAD软件进行仿真分析，其中仿真时间设置为T＝0.5 s，采样频率设置为3.84 k Hz。

2.1 两分支传输线路仿真

如图8所示两分支线路模型，采用110 k V等级电网进行测试（本算法具备通用性，本文选择采用地区电网较常见的110 k V分支线路进行仿真），具体参数设置见表1。

图8 两分支传输线路Fig.8 Transmission line with two tapped legs

表1 仿真系统参数设置Tab.1 Parameters of simulation system

为了验证故障区域判别方法的正确性，利用PSCAD对传输线路上各点的短路故障进行仿真模拟，进而获取线路两端的故障电气量，利用计算的故障指标进行故障区域判断，结果见表2。

表2的仿真实验涵盖了线路的所有可能的分支故障点；由表2的计算结果清楚地显示，本文提出的方法均能够正确判断故障所在的支路，即使在分支节点附近亦能实现可靠判断。

其次为了验证算法在不同故障条件下的判别准确性度，本文完成了大量的仿真实验，包括不同的故障类型、故障距离、过渡电阻。表3选取了部分线路关键位置的判别结果，该计算结果显示在各类典型的故障条件下，本文的算法均能准确判断故障所在支路。

2.2 多分支传输线路仿真

多分支线路模型如图9所示，具体参数同模型2，其中线路总长L＝400 km，假设分支线路均匀出现在主线路上。

为了验证该方法对多分支线路的通用性，假设输电线路主线上发生不同位置、过渡电阻、类型的短路故障，应用本文方法进行初步的故障区域判断。结果如表4所示。

由表4可知，通过区域判定指标，本算例的多分支线路问题可准确缩小为区域1－6（除支路6－8、分支6－7外）、区域2－8（除支路1－2、分支2－3外）的两分支线路问题，或区域2－6（除支路1－2、6－8、分支2－3、6－7外）的单分支线路问题。进而继续采用前文的支路判定指标，直至判定故障支路。

表2 故障区域判断结果（1）Tab.2 Discrimination results of fault section（1）

表3 不同故障类型、过渡电阻下的仿真结果Tab.3 Simulation results under different kinds of faults and transition resistances

图9 多分支传输线路Fig.9 Transmission line with multi tapped legs

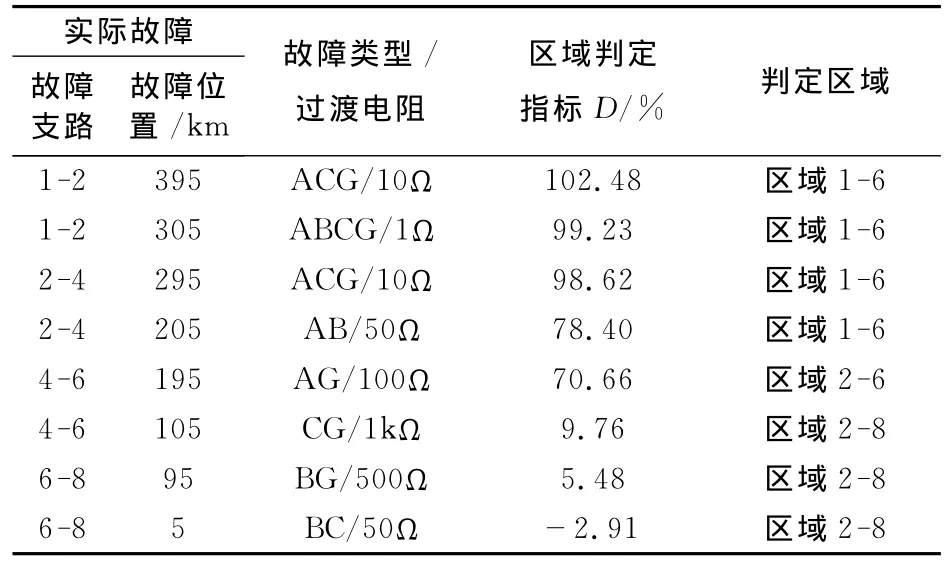
表4 故障区域判断结果（2）Tab.4 Results of faulted section discrimination（2）

3 结语

针对多分支的复杂传输线路，本文提出一种通用性的故障支路判别指标，该指标仅利用线路两端的电压、电流值进行计算，通过与线路分支节点的位置对比，进而判断故障所在分支，最终可转化为传统的双端故障测距问题。经本文的理论证明显示，该方法不仅适用于单分支线路，同样适用于两分支、甚至任意多分支线路；经本文的大量仿真实验表明，该算法在任意的系统运行方式、过渡电阻、故障类型、距离等条件下，均能取得较高的故障判别准确性。

［1］ 王波（Wang Bo）.基于WAMS的高压输电网络故障定位研究（Research on WAMS Based Fault Location for High Voltage Transmission Network）［D］.杭州，浙江大学电气工程学院（Hangzhou：School of Electric Engineering，Zhejiang University），2010.

［2］ 施世鸿，何奔腾（Shi Shihong，He Benteng）.不受TA饱和影响的高压输电线路故障测距算法（Fault location algorithm for HV transmission lines immune to saturation of current transformers）［J］.电力系统自动化（Automation of Electric Power Systems），2008，32（2）：67－71.

［3］ de Morais P C E，Zanetta L C Jr.Fault location in transmission lines using one－terminal postfault voltage data［J］.IEEE Trans on Power Delivery，2004，19（2）：570－575.

［4］ Takagi T，Yamakoshi Y，Yamaura M，et al.Development of a new type fault locator using the one－terminal voltage and current data［J］.IEEE Trans on Power Apparatus and Systems，1982，101（8）：2892－2898.

［5］ 翟永昌（Zhai Yongchang）.实用高压直流输电线路故障测距方法（Practical fault location method of HVDC power transmission line）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（5）：70－73.

［6］ Jiang Joe－Air，Yang Jun－Zhe，Lin Ying－Hong.An adaptive PMU based fault detection／location technique for transmission lines，（I）：Theory and algorithms［J］.IEEE Trans on Power Delivery，2000，15（2）：486－493.

［7］ Jiang Joe－Air，Lin Ying－Hong，Yang Jun－Zhe，et al.An adaptive PMU based fault detection／location technique for transmission lines，（II）：PMU implementation and performance evaluation［J］.IEEE Trans on Power Delivery，2000，15（4）：1136－1146.

［8］ Nagasawa T，Abe M，Otsuzuki N，et al.Development of a new fault location algorithm for multi－terminal two parallel transmission lines［J］.IEEE Trans on Power Delivery，1992，7（3）：1516－1532.

［9］ Girgis A A，Hart D G，Peterson W L.A new fault location technique for two－and three－terminal lines［J］.IEEE Trans on Power Delivery，1992，7（1）：98－107.

［10］Gong Qingwu，Chen Yunping，Zhang Chengxue，et al.A study of the accurate fault location system for transmission line using multi－terminal signals［C］∥IEEE Power Engineering Society Winter Meeting.Singapore，Singapore：2000.

［11］Masayuki Abe，Nobuo Otsuzuki，Tokuo Emura，et al.Development of a new fault location system for multi－terminal single transmission lines［J］.IEEE Trans on Power Delivery，1995，10（1）：159－168.

［12］Yu Chi－Shan，Liu Chih－Wen，Lin Ying－Hong.A fault location algorithm for transmission lines with tapped leg－PMU based approach［C］∥Power Engineering Society Summer Meeting.Vancouver，Canada：2001.

［13］Lin Ying－Hong，Liu Chih－Wen，Yu Chi－Shan.A new fault locator for three－terminal transmission lines using two－terminal synchronized voltage and current phasors［J］.IEEE Trans on Power Delivery，2002，17（2）：452－459.

［14］Lin Ying－Hong，Liu Chih－Wen，Jiang Joe－Air.An adaptive fault locator for transmission lines tapped with a source of generation－using synchronized voltage and current phasors［C］∥IEEE Power Engineering Society Summer Meeting.Seattle，USA：2000.

［15］李胜芳，范春菊，郁惟镛（Li Shengfang，Fan Chunju，Yu Weiyong）.T型支接线路的自适应故障测距算法（Adaptive fault location method for three－terminal transmission line）［J］.电工技术学报（Transaction of China Electrotechnical Society），2004，19（10）：59－64.