如何用SAS软件正确分析生物医学科研资料XVI. 用 SAS 软件实现 2 × 2 列联表资料的统计分析

关雪，胡良平，王琪

·讲座·

如何用SAS软件正确分析生物医学科研资料XVI. 用 SAS 软件实现 2 × 2 列联表资料的统计分析

关雪，胡良平，王琪

编者按

生物统计学是生物学领域科学研究和实际工作中必不可少的工具，在分子生物学迅速发展的今天，生物统计学更显示出了它的重要性。实验设计与数据统计分析是现代生物学的基石，是生物学研究者检验假说、寻找模式、建立生物学理论的有利工具，也是生物学研究者探索微观和宏观生物世界的必备基础知识。对于每天甚至是每时每刻涌现的大量的、以天文数字计量的分子遗传数据，必须借助统计学知识加以分析处理，才能从中获得有意义的信息。“生物多样性数据分析”是开展生物多样性研究的一个重要方面，数据分析能力的高低极大地影响着我们对各种生态学现象认识的深度和广度。现在，电子计算机的普及使得生物统计分析过程大大简化，生物统计分析软件包的普及将生物统计学从统计学家的书本里解放了出来，简化了生物统计分析过程，使之成为生物学研究者的常用工具。本刊特邀军事医学科学院生物医学统计学咨询中心主任胡良平教授，以“如何用 SAS 软件正确分析生物医学科研资料”为题，撰写系列统计学讲座，希望该系列讲座能对生物医学科研工作者有所帮助。

分析定性资料时，首先应正确判断资料所对应的列联表类型；其次根据不同的分析目的，并结合统计分析方法的应用条件，选择合适的分析方法。通常，列联表可分为：2 × 2表（4 类）、R × C 表（5 类）和高维列联表（3 类）以及具有重复测量因素的高维列联表[1]。本期主要介绍 2 × 2 列联表资料统计分析的 SAS 实现。

1　横断面研究设计 2 × 2 表资料统计分析的 SAS实现

在某个时间断面（时点或很短时间内）进行的调查或试验研究中，对一组受试对象同时按两个定性变量来划分，每个定性变量都只有 2 个水平，其目的是了解某个时间点的现状，由此获得的 2 × 2 表资料称为“横断面研究设计的2 × 2 列联表资料”[2]。医学中，通常用于对疾病或健康状况分布特征的描述、对防治措施效果的评价、对疾病与某些因素相互联系的探讨等。

【例 1】为探讨术前 3 d 给予大剂量麝香保心丸对于经皮冠状动脉介入疗法病人心肌损伤的影响，随机选择 133 例2008 – 2009 年拟行冠状动脉造影的不稳定型心绞痛患者，分为对照组和试验组，试验组在常规治疗的基础上加服麝香保心丸。试验前对两组患者的血脂情况进行比较，数据见表 1，试分析两组患者血脂异常率之间是否存在差别[1]。

分析与 SAS 实现：该试验目的是测定试验前两组患者的血脂异常率是否存在差别，可视为横断面研究设计 2 × 2表资料。因总频数 133 大于 40，且理论频数均大于 5，故可用一般χ2检验。具体的 SAS 程序如下：

表1　两组患者血脂测定结果

程序说明：数据步，建立名为 tjfx1 的数据集，建立数值型变量 A、B、f，分别读入原因变量的水平、结果变量的水平和对应单元格中的实际频数。过程步，调用 FREQ 过程，指定频数变量为 f，用 tables A*B 语句表示生成二维列联表资料，斜杠“/”后的选项 chisq要求进行一般χ2检验。SAS 输出结果与结果解释如下：

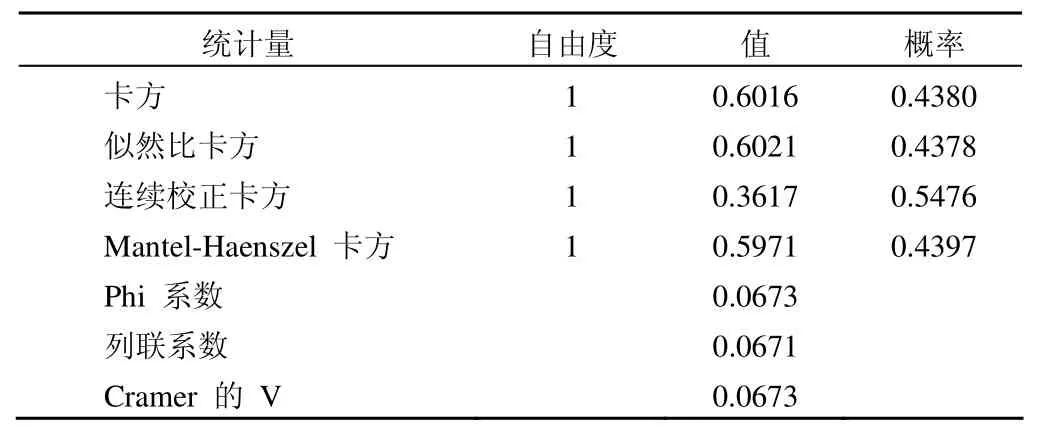
A*B 表的统计量

Fisher 精确检验

统计和专业结论：由于χ2= 0.6016，P= 0.4380 > 0.05，表明两组患者的血脂异常率之间的差别无统计学意义，即两组患者的血脂异常情况相同，差别仅是抽样误差所致。

对于横断面研究设计的 2 × 2 表资料而言，当总例数n> 40 且无单元格的理论频数T＜ 5 时，可选用一般χ2检验；当总例数n> 40 但至少有一个单元格的理论频数 1 ＜T≤ 5 时，可选用校正的χ2检验；当总频数n＜ 40 或至少有一个单元格的理论频数T＜ 1 时，必须选用 Fisher 精确检验。

2　队列研究设计 2 × 2 表资料统计分析的 SAS实现

所谓“队列研究设计的 2 × 2 表资料”，就是依据专业知识，通过对不同暴露水平的对象进行追踪观察，确定其疾病发生情况，从而分析暴露因素与疾病发生之间的因果关系。它是由因溯果的前瞻性研究设计，是论证疾病因果关系的一个重要研究方法。

【例 2】为探讨两种药物治疗胃炎的预后，将胃炎患者随机分为两组，一组患者服用 A药，另一组患者服用 B 药，治愈后追踪观察一段时间，观察胃炎复发的情况，资料见表2。试比较两种药物复发率之间的差异有无统计学意义。

表2　不同药物治疗胃炎的复发情况

分析与 SAS 实现：表 2 资料为来自队列研究设计的2 × 2 列联表资料，可先按横断面研究设计 2 × 2 列联表资料的检验方法考察两组频数分布是否相同，如果不相同，再计算相对危险度RR，并进一步对总体RR值是否等于 1进行假设检验。具体的 SAS 程序如下：

程序说明：建立名为 tjfx2 的数据集，建立数值型变量a、b、f，分别读入行号、列号、每格实际频数；过程步，调用 FREQ 过程，指定频数变量为 f，用 tables a*b 语句表示生成二维列联表资料，斜杠“/”后的选项 chisq 表示要求进行一般χ2检验，选项 cmh 要求输出 Cochran-Mantel-Haenszel 统计量，当列联表为 2 × 2 表时，它可以输出OR（优势比）和RR（相对危险度）估计值及置信区间。SAS 输出结果与结果解释：

a*b 表的统计量

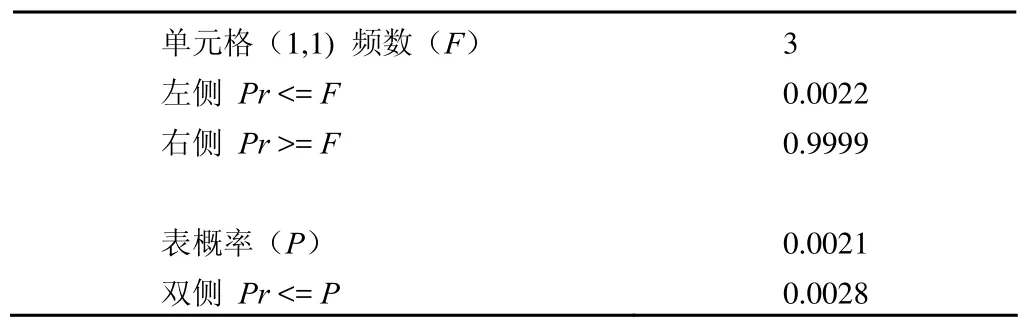
Fisher 精确检验

以上给出了若干χ2检验和 Fisher 精确检验统计量。

a*b 的汇总统计量Cochran-Mantel-Haenszel 统计量（基于表得分）

普通相对风险的估计值（行 1/行 2）

以上第一部分是 Cochran-Mantel-Haenszel 统计量的计算结果，相当于（即Mantel-Haenszelχ2），= 9.7038，P= 0.0018，说明总体RR与 1 之间的差别有统计学意义。第二部分是普通相对风险度的估计值，本资料属于队列研究资料，因此需要看“Cohort”对应的RR值，第 1列（复发）的相对危险度RR= 0.2750，其 95％ 置信区间为（0.1014，0.7458）。

统计和专业结论：因本例资料不满足χ2检验的前提条件，故根据一般 Fisher 精确检验结果可知，P= 0.0028 ＜ 0.01，按照 0.05 的检验水准，拒绝原假设（两药物治疗对应的胃炎复发率相等），接受备择假设（两药物治疗对应的胃炎复发率不相等），可以认为不同药物治疗胃炎的复发率不同；根据RR值及其置信区间，可以认为，一段时间后，使用 A 药治疗胃炎复发的风险是 B 药的 0.2750 倍，换言之，相对于 A 药而言，B 药治疗胃炎更易于复发。

值得注意的是：输出结果中的“（优比）”部分的结果仅当四格表资料来自病例-对照研究设计时才用。另外，与队列研究设计四格表资料分析结果对应的有两部分，第一部分标有“（第一列风险）”，意思是与“第 1 列对应的相对危险度计算结果”；第二部分标有“（第二列风险）”，意思是与“第2 列对应的相对危险度计算结果”。若将资料输入程序时，第 1列上代表研究者关心的“结果”，其RR的计算结果就应采用第一部分的内容，反之，就应采用第二部分的内容。

3　病例-对照研究设计 2 × 2 表资料统计分析的SAS 实现

为什么有些人会患病，而另一些人却没有患病？研究者依据专业知识，提出产生该病的可疑危险因素，寻找与患者条件相近的另一组人作为正常对照者，对他们进行回顾性调查，并按此危险因素的暴露与否将调查者细分为两类，记录两组中“暴露”与“非暴露”的人数，这样收集的资料称为来自病例-对照研究设计的 2 × 2 列联表资料。

【例 3】一项关于吸烟与肺癌关系的病例对照研究，资料见表 3，试探讨吸烟史对肺癌发生的影响[3]。

表3　吸烟史在肺癌及非肺癌组中的情况

分析与 SAS 实现：上表资料为来自病例-对照研究设计的 2 × 2 列联表资料，因总频数 n = 1418 > 40，且无小于 5 的理论频数，可先按横断面研究设计 2 × 2 列联表资料的检验方法考察两组频数分布是否相同，如果不相同，则进一步对总体OR（优势比）是否等于 1 进行检验。具体的 SAS 程序如下：

程序说明：建立名为 tjfx3 的数据集，建立数值变量 a、b、f，分别读入行号、列号、每格实际频数；过程步，调用FREQ 过程，指定频数变量为 f，用 tables a*b 语句表示生成二维列联表资料，斜杠“/”后的 chisq 和 cmh 分别要求进行一般卡方检验和 cmhχ2检验。SAS 输出结果与结果解释：

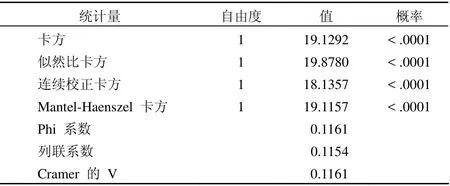
Fisher 精确检验

以上是卡方检验及 Fisher 精确检验法对两组频数分布是否相同的检验结果，χ2= 19.1292，P＜ 0.05，Fisher 精确检验法得P＜ 0.05（双侧），说明两组频数分布不同。

Cochran-Mantel-Haenszel 统计量（基于表得分）

以上三种检验方法是对总体OR是否等于 1 的假设检验，P＜ 0.05，说明总体OR≠ 1。

普通相对风险的估计值（行 1/行 2）

本例属于病例-对照研究设计，故只需看前两行的结果。OR= 2.9738，其 95％ 置信区间为（1.7867，4.9494），不包含 1，说明总体 OR 与 1 之间的差别有统计学意义。

统计和专业结论：这是病例-对照研究设计的 2 × 2 表资料，总体OR与 1 之间的差别有统计学意义，计算得OR= 2.9738，其 95％ 置信区间为（1.7867，4.9494），可认为吸烟史是导致肺癌的危险因素，并且有吸烟史的人患肺癌的概率对于无吸烟史的人患肺癌的概率优势比OR值为2.9738，也就是说有吸烟史的人患肺癌的危险度是无吸烟史人的 2.9738 倍。

4　配对研究设计 2 × 2 表资料统计分析的 SAS实现

所谓配对研究设计 2 × 2 表资料是指按照配对原则，受试者或样品分别接受两种不同的处理方法，每种处理方法的结果都可分为“阳性”和“阴性”两种，数出两种处理方法同时判定为阳性、阴性的频数以及它们结果不一致的频数，将结果列成配对设计的 2 × 2 表形式。其中一种处理方法区分为阳性、阴性的标准即为金标准，医学中常见的金标准有活组织检查、尸体解剖、手术探查和跟踪随访结果等，另一种处理方法区分阳性、阴性的结果与金标准区分结果进行比较，检验其区分能力。

【例 4】为了探讨噬菌体生物扩增法（PhaB 法）直接检测痰结核分支杆菌（MTB）对异烟肼的耐药性的效果，以建立一种特异性强，敏感性高的 MTB 药敏试验方法。现有临床上初步诊断为耐药肺结核的 40 例患者痰标本，用PhaB 法和绝对浓度法分别检测痰 MTB 对异烟肼的耐药性，结果见表 4。以绝对浓度法检测结果为判断标准。试比较两种方法检测结果之间不一致部分的差别是否具有统计学意义，并检测其一致性是否具有统计学意义[4]。

表4　PhaB 法与绝对浓度法检测结果比较

分析与 SAS 实现：绝对浓度法是检测痰结核分支杆菌对异烟肼耐药性的金标准，故该资料为特设金标准的配对设计四格表资料。值得注意的是：若绝对浓度法不是金标准，则仅当检测结果中隐含金标准（即两种检测方法得到的阳性结果都是真阳性，不存在假阳性结果）时，可以按如下的方法进行统计分析。若既没有金标准又不属于隐含金标准的试验研究问题，则没有分析的价值。根据不同的分析目的，有两种统计分析方法。

⑴若原文的目的是为了比较两种检测方法不一致部分的频数之间的差别是否具有统计学意义，应选用配对设计定性资料的χ2检验，即 McNemarχ2检验。McNemarχ2检验分析的 SAS 程序如下：

程序说明：数据步，建立名为 tjfx4 的数据集，建立数值变量 a、b、f，分别读入行号、列号、每格实际频数；过程步，调用 FREQ 过程，指定频数变量为 f，用 tables a*b语句表示二维列联表资料，斜杠“/”后的选项 agree 表示要求进行 McNemarχ2检验，同时计算简单的 Kappa 系数及其 95％ 置信区间。

SAS 输出结果与解释：

McNemar 检验

以上是 McNemarχ2检验的结果，检验统计量为3.5714，P= 0.0588，可认为两种检测方法不一致部分的差别无统计学意义。

简单 Kappa 系数

以上是 Kappa 检验（即一致性检验）结果，Kappa 值为 0.6277，虽然未对其进行假设检验，但这里给出了 Kappa值的 95％ 置信区间（0.3868，0.8685），不包含 0，说明Kappa 值与 0 之间的差异有统计学意义。

⑵若原文的目的是为了检验 PhaB 法、绝对浓度法两种方法的检测结果是否一致，就应采用一致性检验，即Kappa 检验。Kappa 检验分析的 SAS 程序如下：

程序说明：数据步与 McNemarχ2检验部分是一致的；过程步的不同之处在于，去掉了选项 agree，增加“test Kappa”语句要求进行 Kappa 检验，在进行 Kappa 检验的同时，也进行了 McNemarχ2检验。

SAS 输出结果与结果解释：

McNemar 检验

这是用 McNemarχ2检验的结果，结论同前，从略。

简单 Kappa 系数

以上是 Kappa 检验结果，结论同前，从略。

这是对“H0：总体 Kappa = 0”的假设检验结果，Z= 4.1180，双侧P＜ 0.0001，说明两种方法检测结果之间的一致率P0= (23+11)/40 = 85.0％ 与期望的一致率（相当于随机产生的）Pe= (23 × 28/40 + 17 × 12/40)/40 = 53.0％ 之间的差别有统计学意义，即实际一致率比期望的要高，两种方法的检测结果具有较高的一致性。

专业结论：经 McNemarχ2检验可知，两种检测方法之间不一致部分的差别无统计学意义；经一致性检验可知，PhaB 法与绝对浓度法在检测痰 MTB 对异烟肼的耐药性方面具有较高的一致性。

通常最好的结果是，McNemarχ2检验结果P> 0.05 且两个不一致的频数都接近于 0，而一致性检验结果是P＜ 0.05 且观察的一致率符合专业要求（例如，专业上要求观察的一致率大于 85％）。此时，若在专业上，新的方法较金标准经济、便捷，方可认为：可用新方法取代金标准。

参考文献

[1] Hu LP, Wang Q. Scientific research design and statistical analysis of Chinese traditional medicine. Beijing: People’s Medical Publishing House, 2011:199-221. (in Chinese)胡良平, 王琪. 中医药科研设计与统计分析. 北京: 人民卫生出版社, 2011:199-221.

[2] Hu LP, Wang Q. Statistical analysis using SAS software package for data of 2×2 contingency table. J Chin Integr Med, 2009, 7(7):678-682. (in Chinese)胡良平, 王琪. 2×2列联表资料的统计分析与SAS软件实现. 中西医结合学报, 2009, 7(7):678-682.

[3] Li YH. Achievement of statistical analysis of case-control study contingency table data using SPSS. J Pub Health Prev Med, 2007, 18(6):114-115. (in Chinese)李永红. 病例对照研究列联表资料的SPSS分析. 公共卫生与预防医学, 2007, 18(6):114-115.

[4] Bian ZY, Yang YH, He C, et al. Study on the isoniazid susceptibility of mycobacterium tuberculosis in sputum detected by phage amplified biologically assay. Exp Lib Med, 2009, 29(3):219-220, 334. (in Chinese)边泽源, 杨芸红, 何川, 等. 噬菌体生物扩增法直接检测痰标本中结核分枝杆菌异烟肼耐药性的研究. 实验与检验医学, 2009, 29(3): 219-220, 334.

H0检验：Kappa = 0

DOI:10.3969/cmba.j.issn.1673-713X.2012.02.015

作者单位：100850 北京，军事医学科学院生物医学统计学咨询中心

通讯作者：胡良平，Email：lphu812@sina.com