四点接触球转盘轴承载荷分布的影响因素分析

邱 明，史朋飞，陈 龙，李迎春

(河南科技大学机电工程学院，河南洛阳471003)

0 前言

转盘轴承是广泛应用于风力发电机、农业拖车、起重机、建筑机械等回转部位的大型滚动轴承，可同时承受轴向载荷、径向载荷和倾覆力矩作用［1］。四点接触球转盘轴承滚道结构特殊［2］，内、外滚道各由两条中心不重合的圆弧构成。当有载荷作用时，钢球与内外滚道接触承载，假设钢球与内圈上滚道及外圈下滚道的接触为接触对1，钢球与内圈下滚道及外圈上滚道的接触为接触对2。单纯轴向载荷作用于内圈时，钢球与滚道仅有接触对1承受载荷作用;而联合载荷作用下，钢球与滚道间的接触对接触状态复杂。

四点接触球转盘轴承的理论模型［3－4］基于Hertz点接触假设建立，一般认为轴承的变形仅发生于钢球与滚道的接触部位，忽略了套圈变形对接触状况的影响［5］。而实际的应用中，尤其是对大型转盘轴承，内外套圈的有效壁厚相对于直径尺寸较薄，承受重载时易发生变形。由于有限元分析可将套圈及钢球定义为弹性体，并计入Hertz理论未考虑的摩擦，因此，本文基于ABAQUS有限元软件，依据JB/T 2300—1999中某四点接触球转盘轴承建立模型，忽略安装孔及密封圈等特征，重点探讨了影响轴承轴向承载能力，特别是载荷分布的因素及其影响程度。

1 轴向承载能力分析

图1 转盘轴承的受力示意图

四点接触球转盘轴承整体可承受联合载荷作用，如图1a所示。假设轴承外圈固定，在内圈仅承受轴向无偏心载荷Fa作用时，各钢球与滚道的接触状态相同，即钢球与内外滚道仅有接触对1承受载荷作用，如图1b所示。每个钢球所承受的载荷为Q=Fa/(Z·sinα)，其中，Z为钢球个数;α为接触角。按Hertz点接触理论可得到钢球与滚道的最大接触应力值［6］。

1.1 单个钢球—滚道模型的建立

ABAQUS的静力学分析要求模型的约束条件及网格划分合理，否则迭代过程无法收敛［7］。为节省计算时间，针对轴承的轴向载荷作用分析，建立单个钢球—滚道的半模型进行分析［8］。设置外圈固定，内圈可沿轴向移动，并对模型对称面施加对称约束。将钢球与滚道接触处的网格进行细化处理，控制接触处网格单元最小尺寸小于接触椭圆短半轴的1/2。表1为轴承部件的材料属性及网格划分。根据有限元应力云图分析(见图2)，钢球与滚道的接触区域截面呈椭圆，与Hertz点接触理论结果相符。最大应力在钢球表面下的一定深度处，此即Lundberg-Palmgren疲劳寿命理论中的最大动态切应力的位置，正是其反复作用造成了钢球最初疲劳裂纹的出现。

表1 模型的材料属性及网格划分

比较不同轴向载荷作用下有限元分析与理论计算结果，如图3所示，两者间的计算误差很小，最大偏差在4.2%左右，证明所建立边界约束及网格划分合理，而有限元结果低于理论分析结果，也证明理论算法偏安全。

1.2 滚道结构参数对轴向承载能力的影响

初始接触角α及沟曲率半径因数f是影响四点接触球转盘轴承轴向承载能力的关键参数，一般凭借经验选取，有必要分析各因素变化对轴向承载能力的影响趋势及程度，为其取值提供依据。

图2 单个钢球—滚道的有限元应力云图

1.2.1 初始接触角α

接触角α为“钢球—滚道”接触点与钢球球心连线和轴承径向剖面之间的夹角，它对轴承内部的载荷分布、摩擦、润滑等都有影响。当四点接触球转盘轴承内部不存在间隙时，轴承的初始接触角α与装配后接触角一致，而受载后的实际接触角会因钢球与滚道接触点位置发生滑移而变化［9］。在ABAQUS中建立不同初始接触角的四点接触球转盘轴承有限元模型，比较其在不同轴向载荷作用下的接触应力变化，得到的结果如图4所示。相同轴向载荷作用下，初始接触角α为40°～65°，最大接触应力逐渐减小，说明轴承的轴向承载能力随接触角α的增加而变大。但接触角增加过大会使接触椭圆区域趋向滚道边缘，出现应力集中，造成滚道的提前失效。

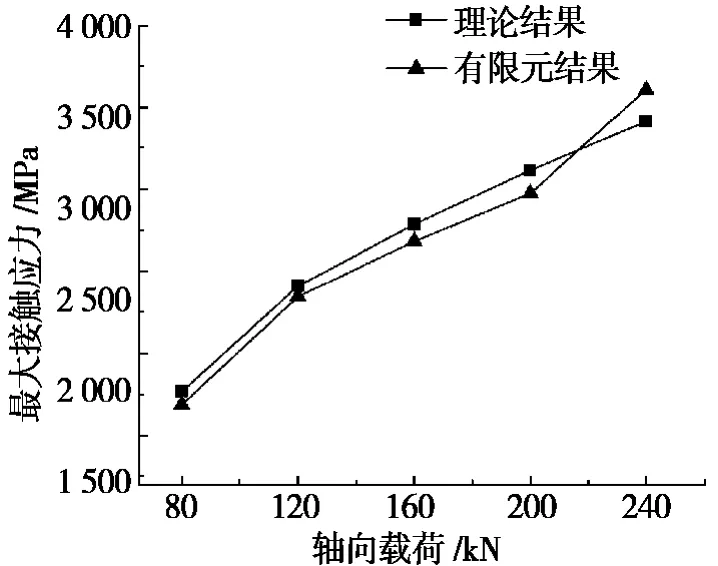
图3 有限元结果与理论分析的对比

1.2.2 沟曲率半径因数f

沟曲率半径因数f是沟道曲率半径r与钢球直径Dw的比值，即f=r/Dw。在轴承的结构参数中，f影响到钢球与滚道的密合程度。四点接触球转盘轴承滚道的沟曲率半径因数比普通轴承的值大，在轴承设计中通常取0.51～0.56。建立不同沟曲率半径因数f的有限元模型进行分析，得到的结果见图5，由图5可看出:相同轴向载荷作用下，随着沟曲率半径因数f的增加，最大接触应力增大，其增加的幅度逐渐减小。对于单排四点接触球转盘轴承的设计而言，为增加轴承的轴向承载能力f值可取0.51～0.52。

2 载荷分布分析

转盘轴承的载荷分布状态决定了固定圈与活动圈之间的相对位移、受载最大钢球位置与最大载荷值［10］。套圈壁厚、游隙及钢球数量是影响轴承载荷分布的重要因素，为此建立整体模型，分析各因素的影响。

2.1 钢球—套圈模型的建立

取四点接触球转盘轴承整体模型的二分之一进行分析，以减少计算时间。分别建立各钢球与内外圈滚道的接触对，设置切向接触为罚接触，摩擦因数为0.04;法向接触为硬接触，当接触压力变为零或负值时，接触对分离，相应接触对的约束去除。在轴承的外圈外表面施加完全约束，限制内圈内表面的绕轴转动;并限制钢球的周向转动，模拟隔离块的作用;设定内圈几何中心为参考点(RP1)，并建立其与内圈内表面的耦合关系;选用六面体缩减积分单元及扫略方式对钢球、内外圈进行网格划分，细化接触位置处网格。有限元模型见图6。倾覆力矩M、轴向载荷Fa施加于参考点(RP1)，其中，M绕Z轴正方向施加。

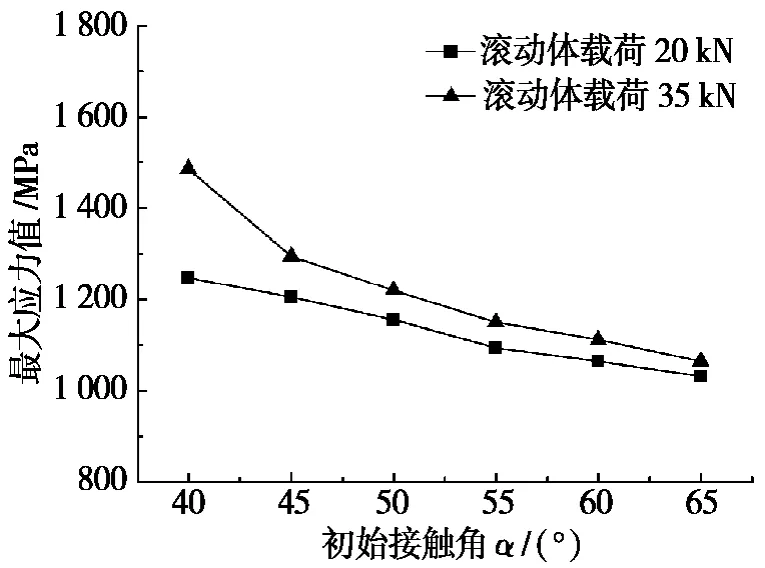
图4 接触应力随α的变化

图5 接触应力随f的变化

2.2 不同载荷作用下的轴承载荷分布

根据所选型号的四点接触球转盘轴承静载荷承载能力曲线，可得其极限载荷为:倾覆力矩M=900 kN·m，轴向载荷Fa=300 kN。另取正常工况载荷:倾覆力矩M=300 kN·m，轴向载荷Fa=200 kN进行分析。假设钢球位置角为－180°～180°，其中，0°为倾覆力矩作用力臂最大位置处。比较两组载荷作用下轴承的载荷分布，如图7所示，极限载荷作用下轴承最大的接触应力为1 863 MPa，低于四点接触球转盘轴承中额定静承载下的许用接触应力，轴承的理论设计安全因数达到2.25。受载后钢球与滚道接触对的承载状态不同，大部分钢球只有一个接触对在承受载荷，即接触对1承受载荷Q1，接触对2承受载荷Q2。还有少量钢球两个接触对同时受载，如图8所示。

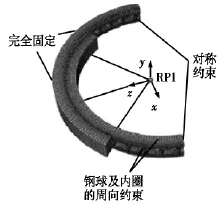
图6 钢球－套圈的有限元模型

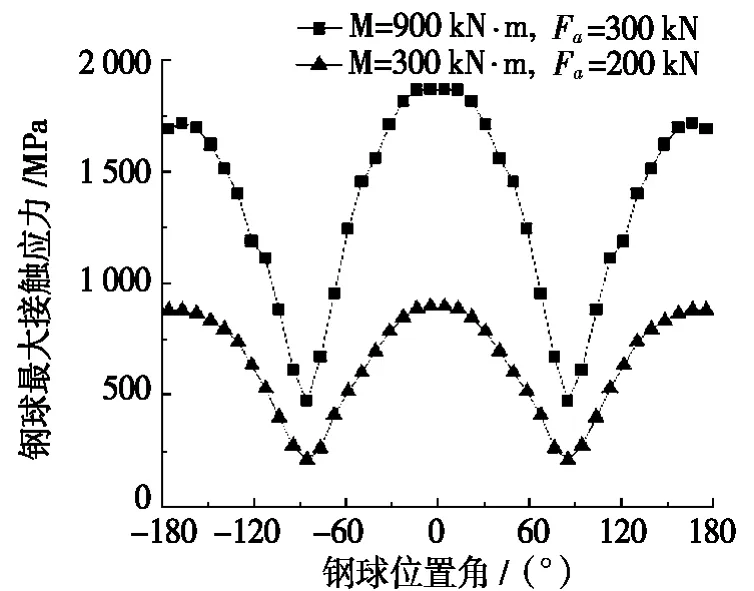
图7 不同载荷作用下的载荷分布

2.3 套圈壁厚对载荷分布的影响

四点接触球转盘轴承套圈的有效壁厚会影响其变形及轴承的载荷分布。保持外圈结构尺寸不变，改变内圈的壁厚，在标准尺寸基础上，对轴承内圈壁厚进行加厚、减薄处理，壁厚的变化量为:10 mm、5 mm、0 mm、－5 mm、－10 mm、－15 mm、－20 mm，分别建立其有限元模型进行分析，得到正常工作载荷下的载荷分布。随着套圈壁厚的减小，各钢球所受载荷均增加，其所承受最大及最小载荷的变化见表2。

图8 轴承载荷分布应力云图

表2 套圈壁厚变化量对轴承载荷分布的影响

当轴承内圈壁厚减少20 mm时，钢球所承受最大载荷仅增加1.8%，而最小载荷值则增加20.5%。图9为标准尺寸下轴承接触对的载荷分布曲线，其中有4个钢球同时有两个接触对在承受载荷作用。随着内圈壁厚的变化量由10 mm至－20 mm变化，同时有两个接触对承载的钢球个数减少，而轴承的最大变形量由0.526 8 mm增加至0.641 6 mm，，轴承的承载能力降低。

2.4 游隙对轴承载荷分布的影响

游隙的存在影响轴承的载荷分布，当受载后轴承的套圈变形量不能消除游隙时，钢球将不与滚道发生接触，接触对不承受载荷作用。为探讨游隙值对轴承载荷分布的影响，本文选取游隙值分别为－0.06 mm、－0.04 mm、－0.02 mm、0 mm、0.02 mm、0.04 mm建立模型分析，轴承的载荷分布如表3所示，游隙为－0.06 mm时，钢球所承受的最大载荷比零游隙下减小4.21%，而最小载荷值则增加26.70%。

表3 游隙值对轴承载荷分布的影响

比较不同游隙下钢球接触对的载荷分布，如图9～图11所示，随着正游隙变化为负游隙，同时存在两个接触对承受载荷的钢球个数增加，即钢球承载区域变大。游隙对轴承整体变形的影响曲线见图12，在游隙值由－0.06 mm变为0.04mm时，轴承整体变形量呈现近似线性的增加，由0.436 8mm增至0.626 8 mm，这说明轴承套圈的刚度随游隙值的增加而减小，适当的负游隙能降低轴承的整体变形量。为提高轴承的承载能力，装配时应使轴承有合适的负游隙。但负游隙过大会造成轴承摩擦力矩增大，因此，游隙的选择应综合考虑转盘轴承的使用要求。

图9 标准尺寸零游隙下轴承的载荷分布

图10 游隙0.04 mm下轴承的载荷分布

图11 游隙－0.04 mm下轴承的载荷分布

2.5 钢球数量对轴承载荷分布的影响

四点接触球转盘轴承有填球孔，其钢球数量不受填球角度的限制，通过调整隔离块，甚至可达到满装要求。取钢球个数为20、30、40、50、60，分别建立有限元模型计算，钢球个数对其载荷的影响曲线如图13所示。随着钢球个数的增加，钢球所承受的最大载荷与最小载荷均减小，但减小的趋势减缓，说明钢球个数的增加可提高轴承的承载能力，但提高程度逐渐降低。此外，钢球个数由20个增加到60个时，其套圈变形量由1.035 0 mm减小至0.640 3 mm，证明钢球数量的增加可有效提高轴承套圈的刚度。

图12 游隙对套圈变形量的影响曲线

图13 钢球个数对钢球载荷的影响曲线

3 结论

(1)有限元法应用于四点接触球转盘轴承载荷分布的分析具有可行性。

(2)适当地增加初始接触角度α、减小沟道曲率半径因数f，可以提高四点接触球转盘轴承的轴向承载能力。

(3)套圈的弹性变形会影响轴承的载荷分布，增加套圈的壁厚、采用适当负游隙、增加钢球的数量，可减小套圈的变形，提高轴承的承载能力，使轴承载荷分布更加合理。

［1］ 徐立民，陈卓.回转支承［M］.合肥:安徽科学技术出版社，1988.

［2］ Amasorrain J I，Sagartzazu X，Damian J.Load Distribution in a Four Contact-point Slewing Bearing［J］.Mechanism and Machine Theory，2003，38(6):479－496.

［3］ 汪洪，陈原.转盘轴承承载能力及额定寿命的计算方法［J］.轴承，2007(2):7－9.

［4］ 郑兰疆，李彦，赵武，等.大型回转轴承的承载性能分析［J］.机械设计与研究，2008，24(2):82－86.

［5］ 余海东，丁晟，张凯之，等.盾构机主轴回转支承轴承刚度及变形特性研究［J］.中国机械工程，2012，22(4):452－457.

［6］ Harris T A.Rolling Bearing Analysis［M］.5 ed.New York:Taylor＆Francis，2007.

［7］ 赵腾伦.ABAQUS6.6在机械工程中的应用［M］.北京:中国水利水电出版社，2007.

［8］ Kunc R，Zerovnik A，Zvokelj M，et al.Numerical Determination of the Carrying Capacity of Large Rolling Bearings［J］.Materials Processing Technology，2004，155/156(1/3):1696－1703.

［9］ Zupan S，Prebil I.Carrying Angle and Carrying Capacity of a Large Single Row of Ball Bearings as a Function of Geometry Parameters of the Rolling Contact and the Supporting Structure Stiffness［J］.Mechanism and Machine Theory，2001，36 (10):1087－1103.

［10］ 陈龙，夏新涛，邱明，等.变桨轴承载荷分布分析［J］.轴承，2010(1):1－4.