一类具扩散的SIR传染病模型的稳定性分析

朱道宇

（贵州民族大学理学院，贵州贵阳 550025）

一类具扩散的SIR传染病模型的稳定性分析

朱道宇

（贵州民族大学理学院，贵州贵阳 550025）

研究一类具有空间扩散的SIR传染病模型，通过讨论线性化方程的特征值得到该模型的染病平衡点是局部稳定的，并利用Lyapunov函数得到该平衡点全局渐近稳定的一个充分条件.

传染病模型；平衡点；渐近稳定

1 引言

目前的很多传染病模型都源于Kermack和McKendrick在文献[1]中首次提出的SIR模型，该模型及其各种推广后的模型的动力学行为已被很多学者进行了深入研究.在生态环境各因素的交互作用中，空间因素是影响生态种群形成和运作的一个重要因素[2-5].在建立生态数学模型时，人们越来越多地意识到空间因素的必要性.从生物学观点来看，每个生物个体都分布于空间中并与周围环境以及附近的其他生物个体相互作用.为了寻找食物，躲避更高的传染风险或者其他目的，个体一般会向种群密度较低的方向扩散，以期有更多的自然资源和生存机会.一般而言，在传染病高发期，个体倾向于向传染群的梯度方向扩散.基于此，本文主要研究一类带空间扩散和非单调发病率的SIR传染病模型的稳定性.

2 无扩散的SIR传染病模型

设种群中的个体分为易感者，染病者和康复者三类，易感者由于与染病者接触而染病，染病者康复后可能因缺少免疫力又变为易感者.设在t时刻易感者，染病者和康复者的数量分别为S(t)，I(t)和R(t)，则由Xiao和Ruan在文献[6]中给出的具有非单调发病率的SIR传染病模型如下：

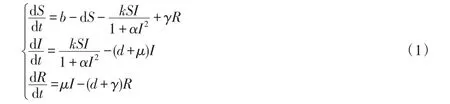
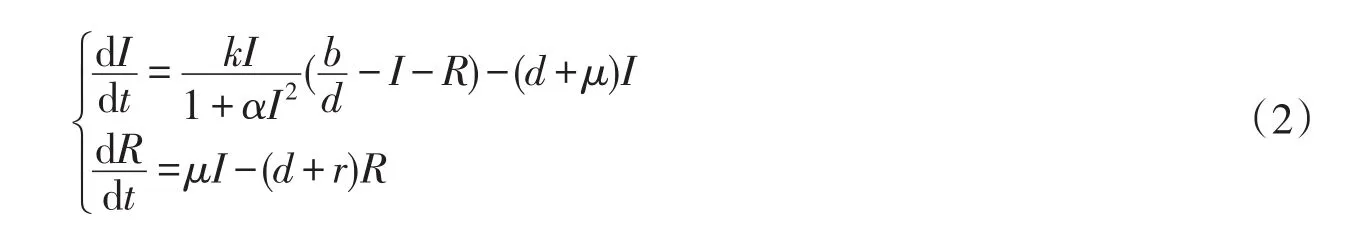
E0=(0,0)叫做无病平衡点，它是一个双曲鞍点，表示传染病的消失；E*=(I*,R*)叫做染病平衡点，表示染病者与康复者的并存.

定理2.1系统（3）的一切正解是最终有界的.

证明将系统（3）的两个方程相加，并令W(t)=I(t)+R(t)，得

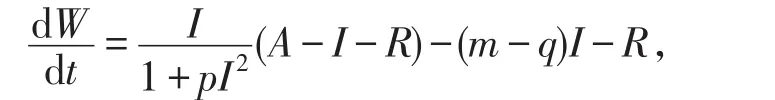
所以对任意的ε＞0，有下面的不等式

其中

因此，由Roth-Hurwitz准则得到平衡点E*=(I*,R*)局部稳定的一个充分条件.

定理2.2系统（3）的染病平衡点E*=(I*,R*)是局部渐近稳定的.

事实上，更进一步地，我们有：

定理2.3系统（3）的染病平衡点E*=(I*,R*)在第一象限内是全局渐近稳定的.

证明构造Lyapunov函数

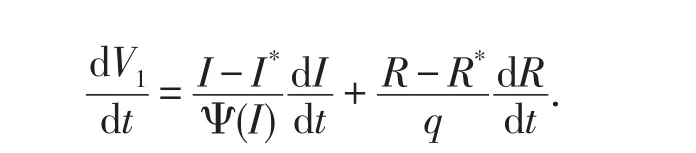
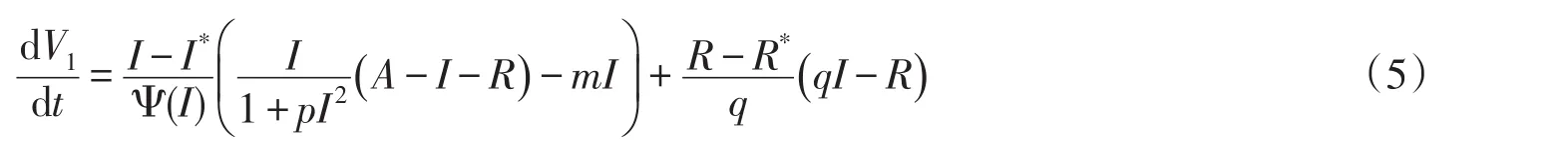
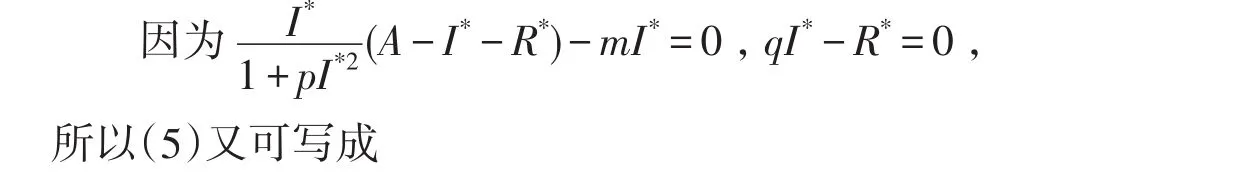
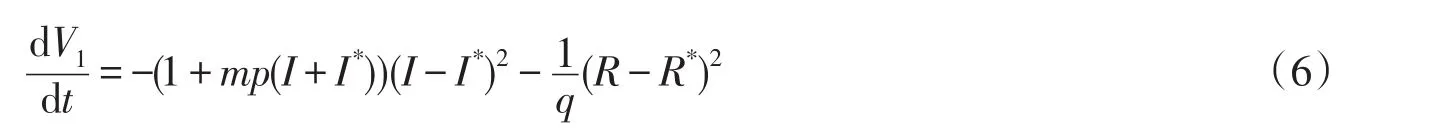
3 带扩散的SIR传染病模型

设易感者I和康复者R在空间中可以随意移动，则与模型（3）对应的具有空间扩散的传染病模型为

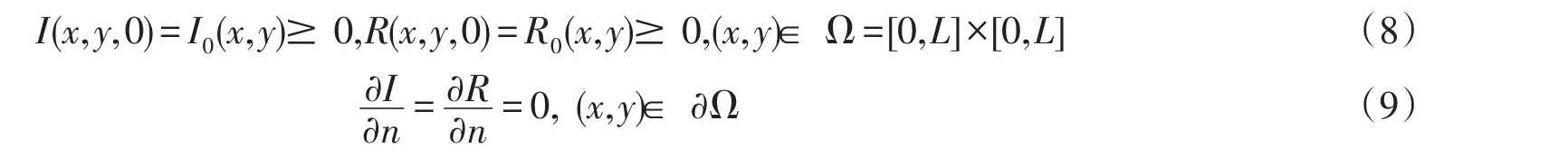
其中n表示边界∂Ω上的单位外法向量.齐次Neumann边界条件说明上述系统是封闭的，在Ω的边界上没有个体移动.下面我们研究扩散系统（7）的相关性质，首先考察解的一致有界性.

定理3.1对于系统（7）的任一解() I(x,y,t),R(x,y,t)，有

证明由系统（7）的第一个方程及条件（8）和（9）知，I(x,y,t)应满足

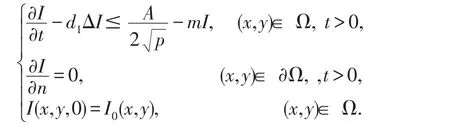
设X(t)是初值问题

证毕.

下面利用线性化方程的特征值以及Liapunov函数法讨论系统（7）的染病平衡点E*=(I*,R*)的局部稳定性和全局稳定性.设0＜μ0＜μ1＜μ2＜…是算子Δ在具齐次Neumann边界条件的Ω上的特征值，令集合

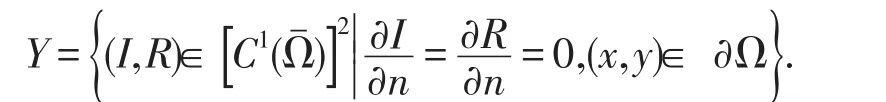
定理3.2系统（7）的染病平衡点E*=(I*,R*)是一致渐近稳定的.

证明系统（7）在平衡点E*处的线性化方程为

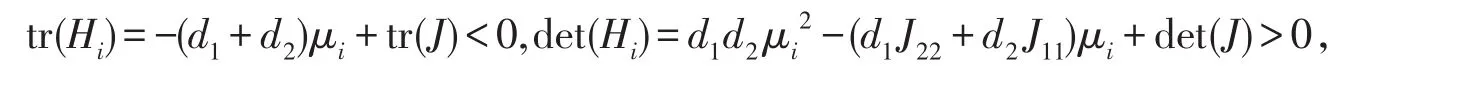
以上两条说明，存在一个与i无关的正常数C，使得对所有的i都有Re()＜C，因此算子A的谱位于{Re(λ)＜C}中，由文献[8]知，系统（7）的平衡点E*=(I*,R*)是一致渐近稳定的.

证毕.

证明构造Lyapunov函数

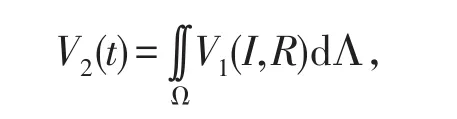
其中V1(I,R)的表达式如（4）式所示.将V2(t)沿着系统（7）的解关于时间t求导，得

因此，系统（7）的平衡点E*=(I*,R*)是全局渐近稳定的.

证毕.

染病平衡点E*=(I*,R*)的全局渐近稳定性意味着，无论感染者和康复者空间扩散得快慢如何，传染病将在一定空间内持久地存在.

[2]Holmes E,Lewis M,Banks J,et al.Partial differential equations in ecology:spatial interactions and population dynamics[J].Ecology,1994,75(1):17-29.

[3]Rass L,Radcliffe J.Spatial deterministic epidemics[M].Washington DC:American Mathematical Society,2003.

[4]Murray J.Mathematical biology[M].New York:Springer,2003.

[5]Wang K,Wang W,Song S.Dynamics of an HBV model with diffusion and delay[J].Journal of Theoretical Biology,2008,253(1):36-44.

[6]Xiao D,Ruan S.Global analysis of an epidemic model with nonmonotone incidence rate[J].Mathematical Bioscience,2007,208(2): 419-29.

[7]Pang P Y,Wang M X.Strategy and stationary pattern in a three-species Predator-Prey model[J].Journal of Differential Equations, 2004,200(2):245-273.

[8]Henry D.Geometric theory of semilinear parabolic equations[M].In:Lecture Notes in Mathematics.New York:Springer-Verlag, 1981.

[1]Kermack W O,McKendrick A G.A Contribution to the Mathematical Theory of Epidemics[J].Proc Roy Soc,1927,115(772):700-721.

Stability Analysis of an SIR Epidemic Model with Diffusion

ZHU Dao-yu
(School of Science,Guizhou Minzu University,Guiyang 550025,China)

An SIR epidemic model with spatial diffusion is investigated.Local stability of the endemic equilibrium of the epidemic model is presented by analyzing eigenvalues corresponding to linearization equation.A sufficient condition is obtained for the global asymptotic stability of the endemic equilibrium by Lyapunov function method.

O29

A

1008-2794（2012）10-0045-06

2012-09-27

贵州民族大学校级科研基金资助项目（201202）

朱道宇（1982—），女，贵州遵义人，讲师，硕士，研究方向：微分方程与动力系统.

Key words:epidemic model;equilibrium;asymptotic stability