线性规划问题规范型算法的改进及计算机实现

高培旺

（闽江学院数学系，福建福州 350108）

线性规划问题规范型算法的改进及计算机实现

高培旺

（闽江学院数学系，福建福州 350108）

线性规划的规范性算法是从一个初始基出发，通过一种单纯形变式求得可行基的方法.提出了求等式约束方程的初始基的方法，该方法不需要计算辅助目标函数的缩减费用，在约束无冗余的假定下经过至多m（等式个数）次迭代后一定得到一个初始基或者问题无可行基的结论，并对规范型算法进行了简化.为了验证改进的规范型算法的计算性能，通过MATLAB编程在计算机上实现大规模数值试验，结果表明，与经典单纯形算法相比，改进的算法平均每次迭代花费更少的执行时间，因而具有更高的计算效率，且随着问题规模的扩大，其计算优越性更明显.

线性规划；可行基；单纯形算法；规范型；计算机实现

1 引言

单纯形法是求解线性规划实际问题非常有效的算法，由于其在选择初始顶点和迭代路径上的灵活性，因而引起了许多研究者的兴趣.对于含有等式约束的线性规划问题，常采用经典的两阶段法[1-2]来求解.在第一阶段单纯形算法中，每个等式需要引入一个人工变量，然后使人工变量之和最小作为辅助的目标函数，以获得问题的一个初始可行解.为了改进第一阶段单纯形算法，人们提出了一种设想：尽可能少地引入人工变量[3-4]或不引入人工变量[5-8].然而，Enge和Huhn[9]，文献[10]都指出，一些无人工变量的初等变换方法实际上隐含着人工变量，只不过字面上没有写出来而已.在初等变换过程中每产生一个新的单位列向量，相当于主枢轴元所在行的人工变量从基中旋转出去.

文献[8]提出了一种线性规划问题的规范性算法，有趣的是，该算法在获得一个初始基（不可行）的前提下，通过简单而巧妙的初等变换，将右手边全部化成非负项，产生了规范型LP（2），继而以变换前最负右手边所对应的等式约束为“目标”，给出了一种单纯形算法.该算法非常类似于“选择进出基变元的新准则”[11-12]，其目的就是在每次迭代过程中使目标函数获得最大的增益，虽然这种方法对某些问题可以减少迭代次数，但逐列搜寻枢轴主元的过程会带来指数时间的计算工作量[9]，从而造成总的计算效率下降，文献[13]通过对中大规模问题的计算试验证实了这一点.注意到这种规范性算法是从一个初始基（不可行）出发求得可行基的过程，因而是一种后处理方法，但文献[8]并没有给出在等式约束条件下求一个初始基的方法.

本文提出了求等式约束方程的初始基的方法，该方法不需要计算辅助目标函数的缩减费用，在约束相容且无冗余的假定下经过与等式个数相同的迭代次数后一定得到一个初始基.如果这个初始基是不可行的，为了方便快捷地获得一个可行基，对规范型算法进行了简化，一是最负右手边所对应的等式约束保持不变，即该等式约束的右手边在变换后仍然为负；二是应用经典单纯形算法的“最负判别数准则”选择枢轴列.为了验证改进的规范型算法的计算性能，我们从线性规划标准测试库NETLIB[14]和整数规划标准测试库MIPLIB[15]中选取了26个典型算例，通过MATLAB编程在计算机上实现大规模数值试验，结果表明，与经典单纯形算法相比，本文提出的改进算法对大部分问题具有更高的计算效率，且随着问题规模的扩大，其计算优越性更加明显.

2 线性规划规范型算法的改进

考虑如下形式的线性规划问题：

（LP）

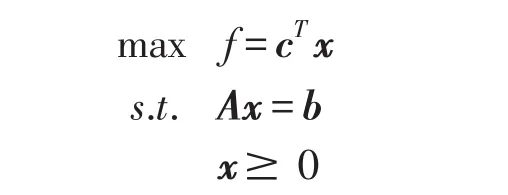
这里，A∈Rm×n（m＜n），且假定rank(A)=m，c、b是相应维数的向量，且b≥0.

在（LP）的等式约束条件中引入非负人工变量向量xArt∈Rm，构造一个人工单位基I∈Rm×m如下：

通过基变量与非基变量的枢轴交换将产生新的基，用B表示，令B-1A=(a¯ij)，B-1b=，显然，当0时，相应的基是可行的；否则，不可行.下面的命题给出了判断问题（LP）不可行性的一个准则.

证明对于x≥0，xArt=0，第i个含有人工基变量的等式约束可以表示为：

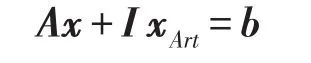
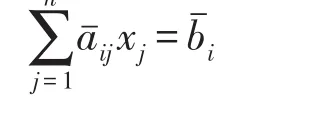
这意味着在x≥0，xArt=0中没有满足第i个约束的变量取值，因而问题（LP）无可行解.类似地，可以证明如果＞0时，有≤0，则问题（LP）亦无可行解.

在无冗余约束的假定下，下列命题明显成立.

命题2假定rank(A)=m，对于含有人工基变量的任意第（i1≤i≤m）个约束，取=，如果=0，则必有＞0.

基于上述命题，我们可以将人工基变量逐一从基中旋转出去，具体算法步骤描述如下：

算法A

步骤1）置i=1，转下一步.

步骤2）如果i=m，算法以获得一个初始基结束；否则，如果，转步骤3）；如果，转步骤4）；如果bi＞0，转步骤5）.

步骤5）取列指标l，满足：ail=1m≤a

j≤xn(aij)，如果ail≤0，算法结束，（LP）无可行解；否则，以ail为主枢轴元进行旋转变换，置i=i+1，返回步骤2）.

在上述算法步骤3）～5）中，如果算法没有以（LP）无可行解而结束，则主枢轴元ail≠0，枢轴交换可以逐行进行下去，这样经过m次枢轴交换，我们就可以获得（LP）的一个初始基，仍用B表示.进一步，若b≥0，这个初始基是可行的，第一阶段算法结束；否则，基B是不可行的，由此出发，我们提出改进的规范型算法来获取（LP）的一个可行基（如果存在），计算步骤可详细叙述如下：

算法B

在第k行中再加入一个人工基变量，转下一步.

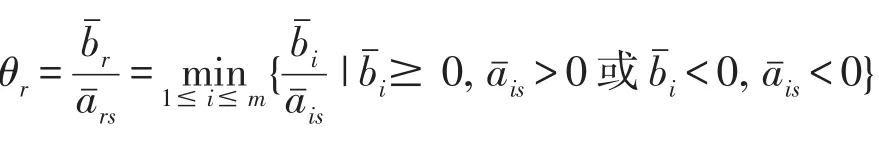
步骤8）如果r=k，算法结束，（LP）的一个可行基已经取得；否则，返回步骤7）.

通过执行上述算法步骤，我们或者获得原问题的一个基本可行解，或者得到问题无可行解的事实.

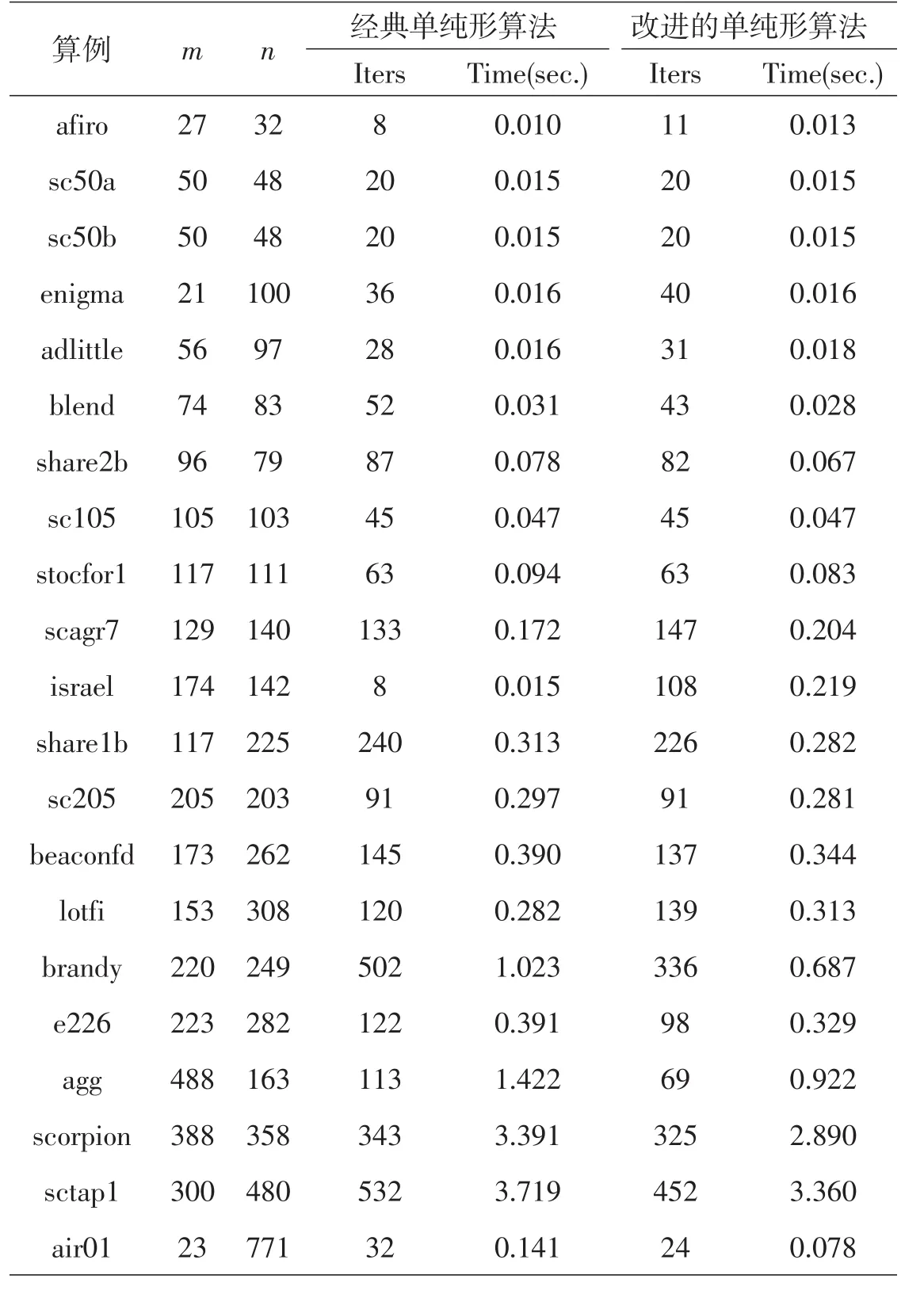
表1 第一阶段问题经典单纯形算法和新的单纯形算法的计算比较

3 规范型算法改进的计算机实现

为了验证改进的规范型算法的计算性能，本文从线性规划标准测试库NETLIB[14]和混合整数规划标准测试库MIPLIB[15]中选取了26个典型算例，其中，问题air01、enigma、lp41、mod010属于整数规划问题，我们只求解其相应的线性规划松弛问题的解.接下来，我们使用MATLAB V7.1语言对经典单纯形算法和改进的规范型算法进行了编程，在Lenovo PentiumM计算机上执行数值试验，以对两种算法的计算效率进行比较.数值试验的环境是完全相同的，计算结果如表1所示，其中，Iters表示求解线性规划问题所需要的枢轴（迭代）数，Time表示所耗费的总的计算时间（单位为秒）.

从表1我们可以看到，改进的规范型算法在每一个问题上平均迭代一次所耗费的计算时间都要比经典的单纯形算法少，并且，改进的规范型算法在14个问题上比经典的单纯形算法所用的迭代次数少，在5个问题上与经典的单纯形算法所用的迭代次数持平，即使在7个问题上比经典的单纯形算法所用的迭代次数多，除问题israel外，相差也不大.尤其是，随着问题决策变量数的增多，规模的扩大，改进的规范型算法一般所用的计算时间更短、计算效率更高.

续表1

4 结束语

本文对文献[8]的规范型算法作了适当的改进，提出了经过至多m步迭代获得一个初始基的方法.如果这个基是不可行的，就用改进的规范型算法产生可行基.从数值试验的结果来看，该算法在大部分问题上比经典单纯形算法所用的迭代次数和所耗费的计算时间要少，尤其在一些较大规模的问题上，其计算优越性更加明显，因而该算法在枢轴方法中是有竞争力的.另外，该算法可以对右手边为负的不等式约束：A1x≤b1不作任何变换，直接添加松弛变量，因而计算处理更方便，也利于节省存储空间.

美中不足的是，改进的规范型算法并不是在所有问题上都比经典单纯形算法好，这也许与驱动行k的选择有关.规范型算法的原理就是将驱动行的左边作为目标函数，应用经典单纯形的枢轴准则选择枢轴行，以使驱动行的右边取值单调递增，直到变成零，则产生一个可行基.于是我们设想，如果选择距离算法A产生的初始点最近的约束超平面作为驱动行，计算效果会否更好？也就是驱动行的右边能更快地达到非负取值.这将留待以后作进一步研究.

[1]许万蓉.线性规划[M].北京：北京理工大学出版社，1990.

[2]黄红选，韩继业.数学规划[M].北京：清华大学出版社，2006.

[3]白岩.线性规划中两阶段法的简便计算法[J].长春师范学院学报（自然科学版），2005，24（5）：1-3.

[4]孙可.线性规划两阶段法的改进算法[J].运筹与管理，2000，9（1）：79-83.

[5]江树彬，周传世.解线性规划问题的一种半单纯形法[J].华南理工大学学报，1995，23（6）：93-99.

[6]Arsham H.Initialization of the simplex algorithm:An artificial-free approach[J].SIAM Review,1997,39(4):736-744.

[7]李炜.求线性规划初始可行基的新方法[J].运筹与管理，2004，13（1）：7-10.

[8]高国成，王卓鹏，刘晓妍.线性规划问题的规范型算法[J].运筹与管理，2004，13（3）：35-38.

[9]Enge A,Huhn P.A counterexample to H Arsham's"Initialization of the simplex algorithm:An artificial-free approach"[J].SIAM Review,1998,40(4):1-6.

[10]高培旺.关于解线性规划问题的一种半单纯形法的注记[J].南通大学学报（自然科学版），2011，36（1）：19-21.

[11]王全文，吴育华，吴振奎，等.单纯形法选择进出基变元的一个新准则[J].数学的实践与认识，2009，39（14）：75-81.

[12]申卯兴，叶微，刘毅，等.单纯形法中枢轴元素选取准则的改进[J].计算机工程与应用，2003，25（1）：57-58.

[13]高培旺.关于“单纯形法选择进出基变元的一个新准则”的计算效率[J].河南工程学院学报（自然科学版），2012，24（2）：61-64.

[14]Dongarra J,Golub G,Grosse E,et al.Netlib and NA-Net:Building a scientific computing community[J].IEEE Annals of the history of computing,2008,30(2):30-41.

[15]Bixby R E,Ceria S,McZeal C M,et al.An updated mixed integer programming library:MIPLIB 3.0[J].Optima,1998,54(1):12-15.

Improvement and Its Computer Implementation of a New Algorithm for Linear Programming

GAO Pei-wang
(Department of Mathematics,Minjiang University,Fuzhou 350108,China)

A new algorithm for the normalized form of linear programming starts from an initial basis and then uses the simplex variant to achieve a feasible basis.This paper presents a method for finding an initial basis of the equality constraints,which does not need to compute the reduced costs of the auxiliary objective function, and under the assumption of no redundancy uses at most m iterations(equal to the number of equality constraints)to get an initial basis or the conclusion of no feasible basis.Furthermore,an improved algorithm of the normalized form is proposed to achieve a feasible basis conveniently and quickly.In the improvement,one is to keep the equality constraint with the most negative right-hand side unchanged,and the other is to apply the rule of the classical simplex method to choose the pivot column.Finally,a computer implementation is accomplished to test the computational performance of our improvement in comparison with the classical simplex algorithm.The computational results show that our improved algorithm averagely spends less executive time at each iteration than the classical simplex algorithm.

linear programming;feasible basis;simplex algorithm;normalized form;computer implementation

O221.1

A

1008-2794（2012）10-0018-05

2012-09-20

闽江学院人才引进基金资助课题“线性规划枢轴算法的大规模计算比较分析及改进”（MJ2012001）

高培旺（1964—），男，湖南宁远人，教授，博士，研究方向：最优化理论及其应用．