P，Q-对称熵损失函数下Pareto分布参数的Bayes估计

张萍，邓永坤，乔路芳

（中国矿业大学理学院，江苏徐州 221116）

P，Q-对称熵损失函数下Pareto分布参数的Bayes估计

张萍，邓永坤，乔路芳

（中国矿业大学理学院，江苏徐州 221116）

在P，Q-对称熵损失函数下，讨论了Pareto分布参数的Bayes估计.当先验分布为伽玛分布时，给出估计的精确形式.最后证明了其容许性.

Pareto分布；Bayes估计；P，Q-对称熵损失函数；可容许性

Pareto分布是意大利经济学家Vilfredo Pareto（1848-1923）提出的一种收入分布方式[1].迄今为止，Pareto分布不仅应用于经济收入模型，在其他物理、生物等领域也得到了广泛的应用.吴喜之[2]论述了关于Pareto分布参数估计的一些进展.

含有两个参数的Pareto分布的密度函数如下：其中a＞0为尺度参数，θ＞0是形状参数.

目前已有人研究了平方损失函数，熵损失函数及Q-对称熵损失函数下Pareto分布参数的Bayes估计.李艳颖[3]讨论了在平方损失函数和Q-对称熵损失函数下Pareto分布参数的Bayes估计.李凡群[4]讨论了在熵损失函数下Pareto分布参数的Bayes估计.杜宇静等[5]在P，Q-对称熵损失函数下讨论了指数分布参数的估计.这里主要研究在损失函数为P，Q-对称熵损失函数时，Pareto分布参数的Bayes估计.

1 基本概念

定义1[5]P，Q-对称熵损失函数定义为：

其中p,q∈R+,δ为θ的估计.

定义2[6]设总体X的分布函数为f(x;θ)，其中参数θ为随机变量，取θ得先验分布为π(θ)，如果在所有的决策函数集合D中存在一个决策函数d*(X)，使得对集合D中的任何决策函数d(X)都满足：

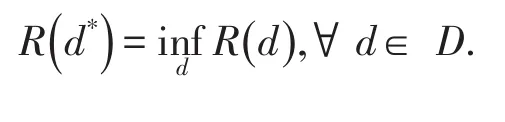
我们把d*()

X称为θ的Bayes估计量.

Pareto分布的密度函数引言中已给出.

设X服从Pareto分布，X1,X2,…,Xn是来自总体为n的简单随机样本，x1,x2,…,xn为X1,X2,…,Xn的观测值，由（1）得X1,X2,…,Xn的联合密度函数为：

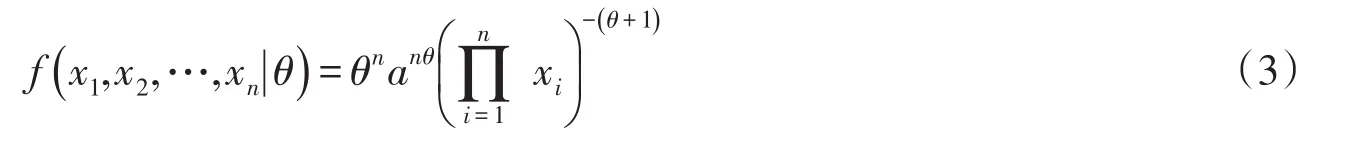
θ未知，下面对它进行估计.

2 参数θ的Bayes估计

定理1当损失函数为P，Q-对称熵损失函数（2），先验分布为任一分布π(θ)，Pareto分布的参数θ的Bayes估计为

证明设δ(X)为θ的任一估计，在P，Q-对称熵损失函数（2）下，δ(X)对应的Bayes风险为

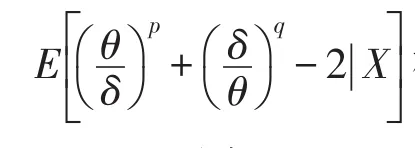
又因为

利用极值理论及定义2知（6）式的极小值即为参数θ的Bayes估计.

现对（6）式关于δ求导并令其等于0，为下式：

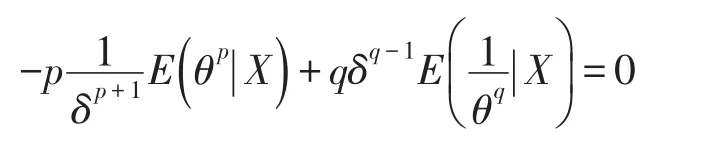
整理后解得

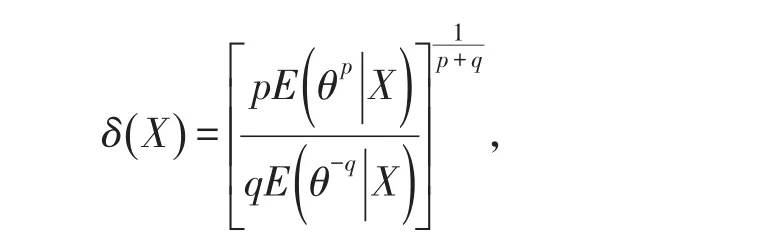
它即为所求参数θ的Bayes估计（4）式.

得证.

设X1,X2,…,Xn服从Pareto分布，且相互独立，x1,x2,…,xn是X1,X2,…,Xn的观测值，θ是未知参数，当给定一个确定的先验分布时，参数θ的Bayes估计的精确形式由下面的定理给出.

定理2取损失函数为P，Q-对称熵损失函数（2），当参数θ的先验分布为伽玛分布Ga(α,λ),即

则Pareto分布参数θ的Bayes估计为：

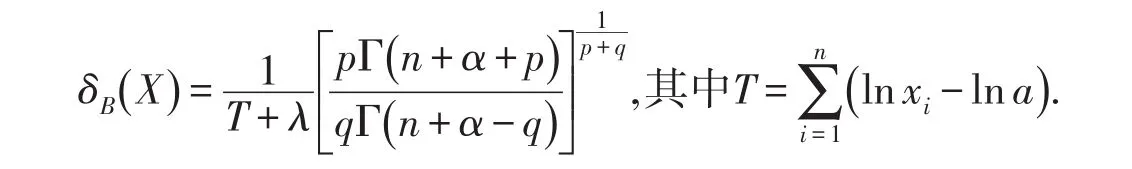
证明由（3）、（7）两式可得θ的后验概率密度函数为：

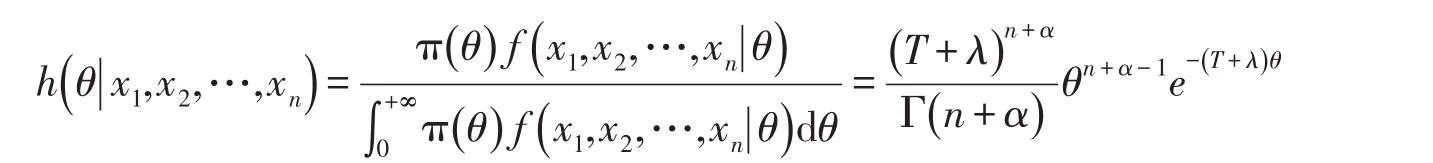
可看出后验分布服从Ga(n+α,T+λ)分布.只要求出E(θp|X)和E(θ-q|X)，代入定理1，即可得参数θ的Bayes估计.

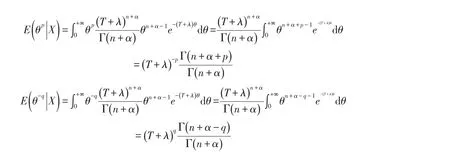
3 Bayes估计的容许性

引理[7]给定一个统计决策问题，δB(X)是在给定θ的某个先验分布π(θ)之下的Bayes解，若δB(X)的Bayes风险Rπ(δB(x))＜∞，则δB(X)必是此统计决策问题的容许决策函数.

定理3定理2中，损失函数为P，Q-对称熵损失函数（2）时，Pareto分布的参数θ的Bayes估计

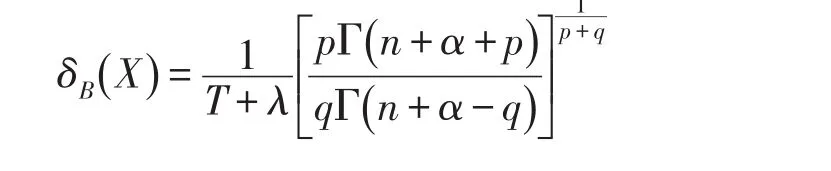
是可容许的.

证明取损失函数为P，Q-对称熵损失函数（2），Pareto分布参数θ的Bayes风险函数为

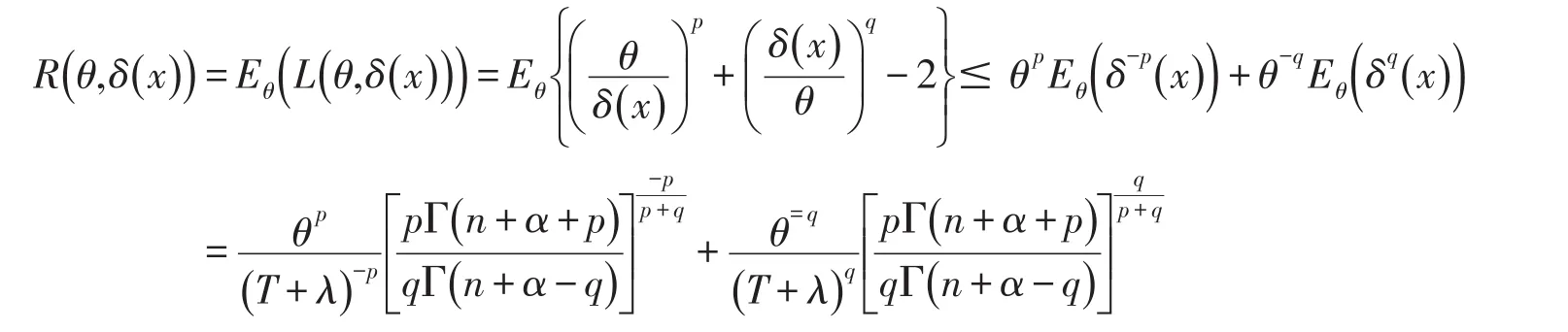
从而有

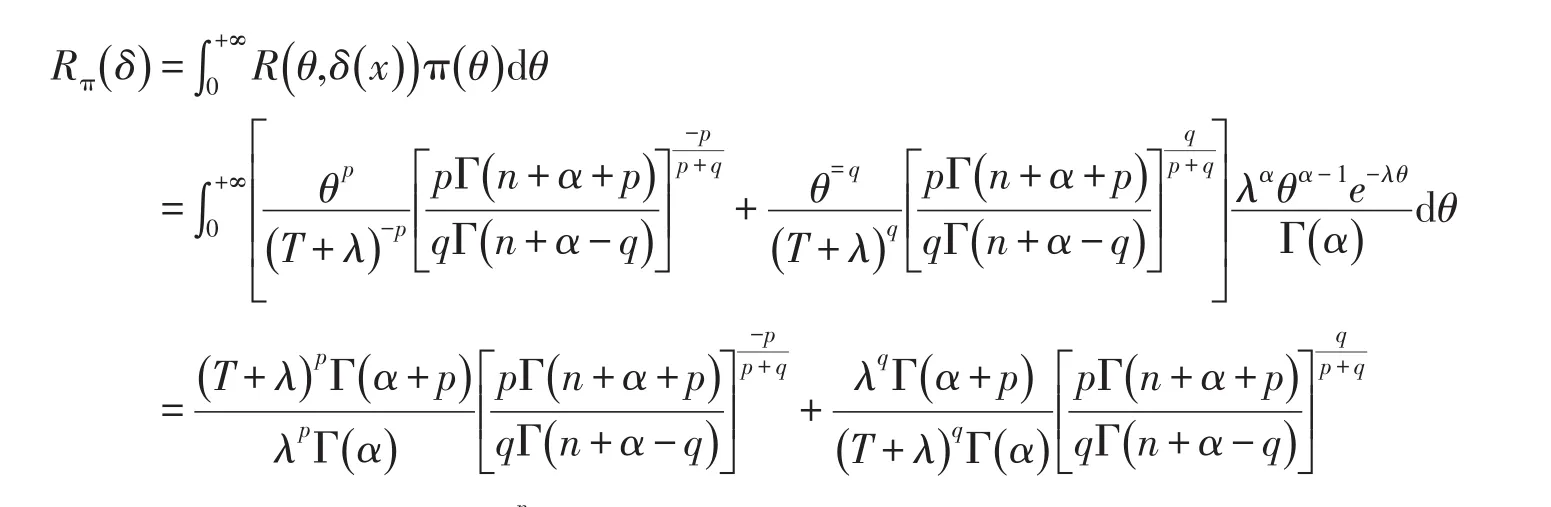
是可容许的.

[1]Pareto V.Cours Economic Politique[M].Lausanne and Paris：Rouge and Cie，1987.

[2]吴喜之.现代贝叶斯统计学[M].北京：中国统计出版社，2000.

[3]李艳颖.Pareto分布参数的Bayes估计[J].四川理工学院学报，2010，23（3）：275-277.

[4]李凡群.熵损失下Pareto分布参数估计[J].安徽电子信息职业技术学院学报，2006，22（5）：73-74.

[5]杜宇静，孙晓祥，尹江艳.p，q-对称熵损失函数下指数分布的参数估计[J].吉林大学学报，2007，45（5）：764-766.

[6]师义民，徐伟，秦超英，等.数理统计[M].北京：科学出版社，2002.

[7]范金城，吴可法.统计推断引导[M].北京：科学出版社，2001.

The Bayesian Estimation of Scale Parameter of Pareto Distribution under P,Q-Symmetric Entropy Loss Function

ZHANG Ping,DENG Yong-kun,QIAO lu-fang
(School of Sciences,China University of Mining and Technology,Xuzhou 221116,China)

Under P,Q-symmetric entropy loss function,this paper first gives the general form of Bayesian estimation.Then,the exact form of Bayesian estimation is given under the condition of giving prior distribution of parameter.Lastly,the paper proves the admissibility of the Bayesian estimation.

Pareto distribution;Bayesian estimation;P,Q-symmetric entropy loss function;the admissibility

O177

A

1008-2794（2012）10-0023-04

2012-09-06

张萍（1986—），女，山西运城人，中国矿业大学理学院2010级硕士研究生，研究方向：数理统计.