基于KUKA 6自由度机器人的误差分析与仿真

魏厚忠， 薛 丹， 焦立奇， 白文峰

（长春工业大学电气与电子工程学院，吉林长春 130012）

0 引 言

解决机器人问题首先必须建立相应的动力学和运动学模型，在此前提下分析和建立误差模型。误差修正的好与坏将直接影响到控制精度，产生误差的原因有很多，如机器人各机械组件以及载荷的质量、重心和惯性，电机的转矩、传动力矩、摩擦转矩、重力矩、科里奥利力矩、惯性矩和支承力矩，还有轴位、轴速度、轴加速度等。以前很多研究减少误差的算法大多以直接误差补偿为主，这种方法需要大量的数据做统计学的支撑，文中通过在KUKA机器人系统里嵌入专家PID算法以及加上特定补偿的算法，成功将误差控制在0.01mm以内。

图1 6自由度KUKA机器人

1 机器人动力学模型的确定

相对机器人运动学而言，机器人动力学问题显得异常复杂。但同时机器人的动力学研究变得越来越重要，尤其在以高速重载自动设备需求日益强烈的今天，动力学问题越发突出。动力学分析是机器人控制、结构设计与驱动器选型的基础。目前，分析机器人动力学的常用方法主要有拉格朗日法、牛顿－欧拉法、虚功原理法及凯恩方程等，文中将以最为经典的前两种方法为基础建立动力学模型。

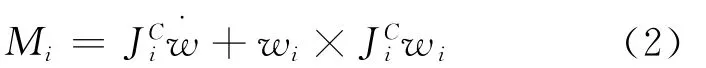
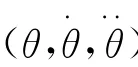
这样计算出每一个构件质心的线加速度和角加速度，再代入牛顿－欧拉方程式，由此可求出作用在每一个构件（第i构件）质心的惯性力和力矩。

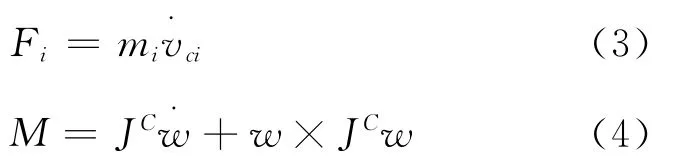
分析动力学的基础是达郎伯原理和虚位移原理。达郎伯原理引入惯性力的概念，使我们能够用解决静力学平衡问题的方法来处理动力学问题。虚位移原理引入虚位移和虚功的概念，给出了处理非自由质点系平衡问题的方法来处理动力学问题。将两个原理结合起来，可推出质点系动力学普遍方程和拉格朗日方程［1］。

对具有N个自由度的机器人操作机构，拉格朗日方程式由N个二阶非线性微分方程构成的方程组为：

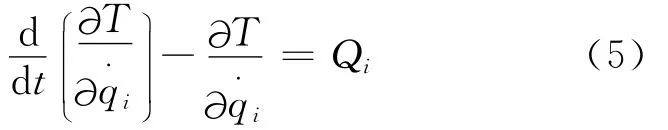
式中：T——系统动能；

Qi——包括重力在内的外力对应于第i个广义坐标的广义力，i＝1，2，…，n。

引入广义力的量Q：

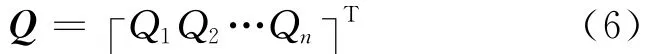
由数量对向量微分的法则，得

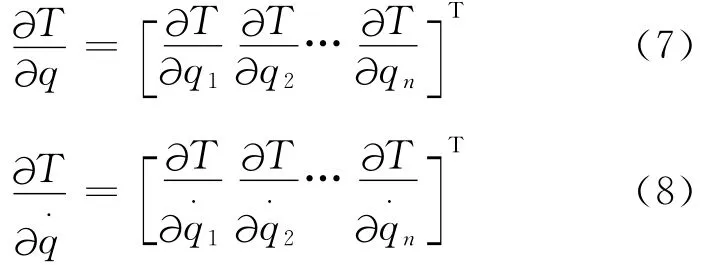
将式（5）写成向量方程形式为：

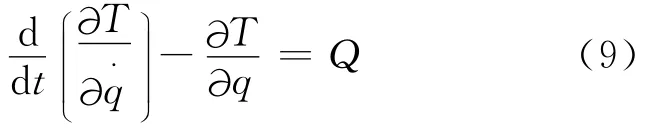
系统总动能T等于各构件动能之和：

式中：M——n＊n矩阵。

设向量Y表示广义力中的除驱动力以外的广义力，则有

则机器人操作器动力学方程的一般形式可写为：

令

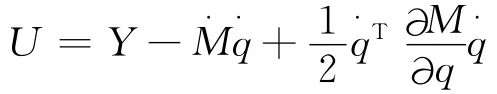
再将上面相应的式子进行微分处理，最终可以得到如下结果：

1）如果是求解直接动力学问题，可用下式求得：

2）如果是求解间接动力学问题，可用下式求得：

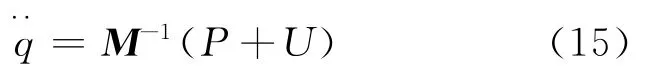
2 运动学模型的确定

建立6自由度机器人模型，一个6轴串联机械臂，得到机器人连杆坐标系，根据D-H法得到机械臂位姿的变换矩阵如下：

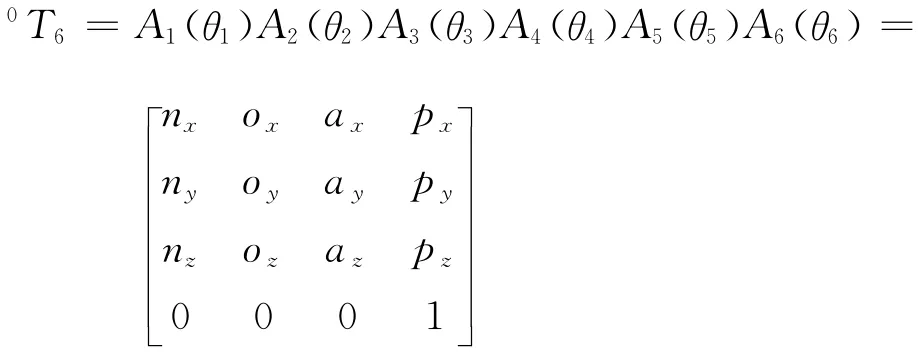
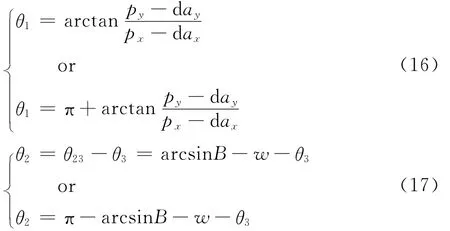
式中：An——根据D-H法建立的机械臂各个关节的变换矩阵。

其中

设在连续轨迹的起始点和终点机器人的姿态为（Ψ0，θ0，φ0）和（Ψ1，θ1，φ1），机器人运动连续平滑，姿态角度随时间做线性变化。在时刻ti（t0＜ti＜t）手部姿态角为：

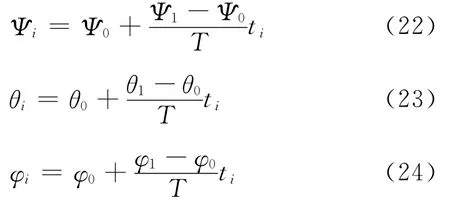
把姿态角和相应的位置值代入文中求出的机械臂逆运动学方程，就可以得出关节空间下的θ1，θ2，…，θ6值。同时，注意这些θ1，θ2，…，θ6值可能会有多解，由机构的奇异问题产生的无穷解，或无解（不可达）。对于多解程序会自动选择离上一个路径最近的解，保证机械臂各个旋转轴运动连续［2］。

6轴机械臂的控制算法使机器人对输入空间曲线计算出各关节的电机控制命令，使机器人沿曲线运动。同时，计算公式中各参数用符号表示，能够运用到各种类似结构的机器人控制。控制算法中多项式插值法使机械臂各关节运动的速度和加速度连续，避免运行生成的机器指令违背物理规律，不能正确执行任务。文中方法计算效率很高，100个点能在2s内计算完成。计算公式是单变量参数方程的形式，在运动的同时计算后面几点，能适应实时控制的要求。

3 误差分析

通过对机器人动力学模型的建立可以发现，在广义力里面包含太多复杂力，这些力也会给机器人的精确控制带来更多的难题。为了简化和系统分析这些力带来的误差，特将广义力Y＝自身惯性力＋负载惯性力＋其它综合惯性力集合。如果用单一控制算法来控制这个广义力，控制效果肯定不好，如果在控制轴上形成轴放大，控制精度肯定达不到要求。为了消除这些误差，文中在KUKA机器人控制系统中采用专家PID和固定误差补偿的方法进行修正误差，专家控制PID的控制系统框图如图2所示。

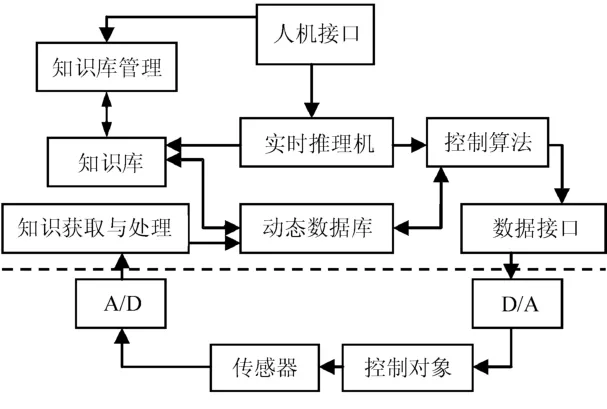
图2 专家控制PID的控制系统框图

知识库包括事实集、经验数据、经验公式和规则集；信息获取与处理是通过底层闭环控制系统的反馈信息和输入信息获取控制系统的误差、误差变化量，以及系统动态特征信息（超调量上升时间等）。信息处理包括必要的特征识别和滤波等；控制算法集合中存放有控制策略和控制方法，如PID，PI，fuzzy和神经控制等；实时推理机是根据一定的推理策略从知识库中选择有关的知识，对所提供的控制算法、事实，以及实时采集的系统特征数据进行推理，直到得出相应的最佳控制决策，用决策结果指导控制作用；动态数据库是用来存放推理过程中用到的数据、中间结果、实时采集与处理的数据［3］。

根据广义力等式可以建立KUKA机器人被控对象的控制系统示意图，如图3所示。

4 仿真与实验数据研究

根据6自由度KUKA机器人可以建立一个6阶传递函数，对相应的采样时间定为1ms，采用专家PID设计控制器［4］，在仿真过程中，ε取 0.001，可以得到误差响应曲线，如图4所示。

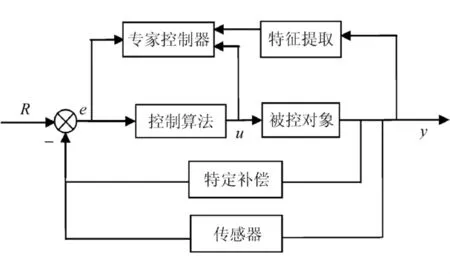
图3 控制系统示意图

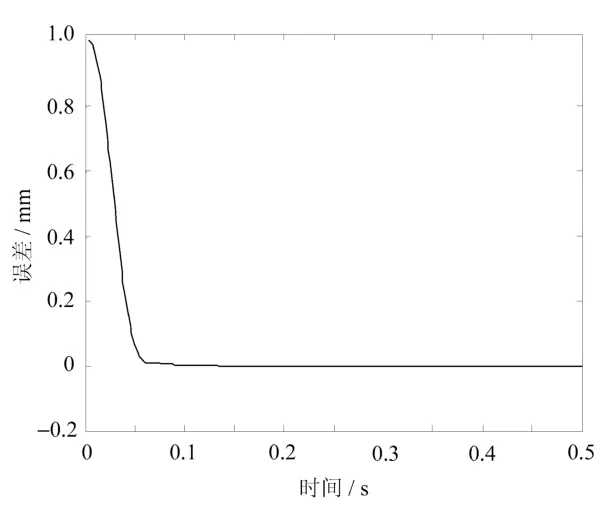
图4 理想误差响应曲线

以上仿真图形主要针对负载惯性力对机器人控制精度的误差仿真［5］，由误差响应图可以知道，专家PID算法可以很好地解决负载惯性力对机器人带来的误差，对其它综合惯性力误差通过特定误差补偿的方式进行。根据KUKA机器人特定误差补偿标定前后的实验数据见表1。

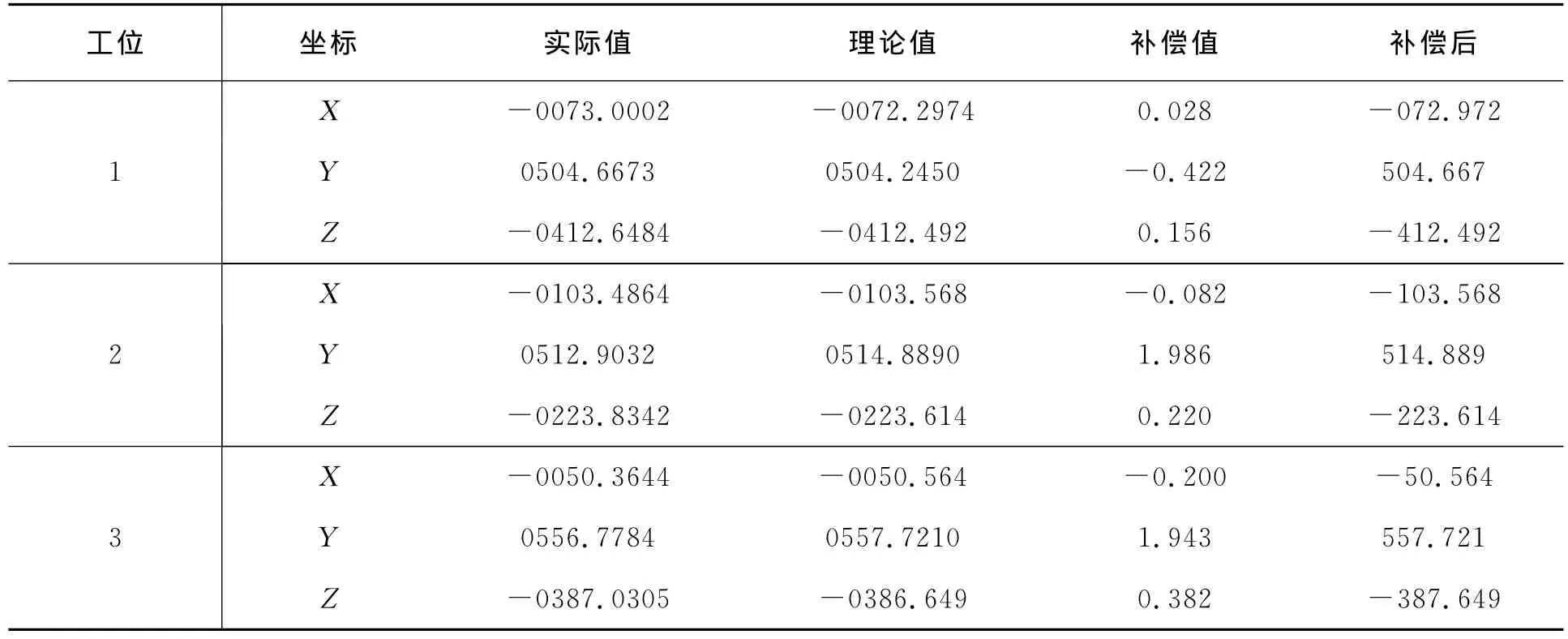
表1 实验数据

通过对几个点的误差补偿来看，补偿值都是由相应的理论值减去实际值而得到，相应值的取得都是借用一定的标定工具和传感器［6－8］，使机器人工作精度从最大误差0.04mm降到0.003mm。补偿示意图如图5所示。

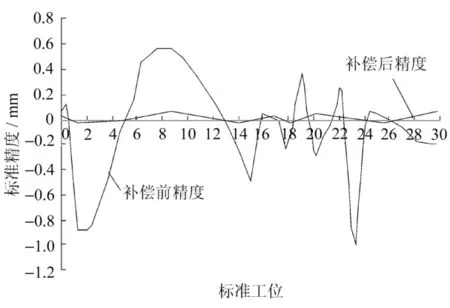
图5 补偿示意图

5 结 语

建立了机器人动力学和运动学模型，对模型的分析可以得出很多误差因素，通过专家PID对负载惯性力的研究和借助外部工具进行特定误差补偿研究，两种方法都可以使误差修正在一定的范围内。通过仿真结果可知，误差修正精度会越来越好，综合起来将会使整个机器人的控制精度更高。

［1］ 马履中，周建忠.机器人与柔性制造系统［M］.北京：化学工业出版社，2007.

［2］ 于靖军，刘幸军，丁希仑，等.机器人机构学的数学基础［M］.北京：机械工业出版社，2008.

［3］ 张永贵.喷漆机器人若干关键技术研究［D］：［硕士学位论文］.西安：西安理工大学，2008.

［4］ 许玉昆，陈彬，尤传富.基于神经网络PID在直流伺服电机中的应用［J］.长春工业大学学报：自然科学版，2010，31（6）：679-682.

［5］ 张静.MATLAB在控制系统中的应用［M］.北京：电子工业出版社，2007.

［6］ 陈明濂.速度和负荷对机器人位置精度的影响［J］.机器人，1988（1）：19-21.

［7］ 卢燕会.工业机器人工作空间和误差补偿的分析与仿真［D］：［硕士学位论文］.焦作：河南理工大学，2010.

［8］ Saha S K.Introduction to robotics［M］.北京：机械工业出版社，2009.