弱拟充足半群
高振林, 邢晓丹
(上海理工大学理学院,上海 200093)
1 乘充足断面的定义
半群S上的格林*-关系L*和R*定义为:
a.L*b当且仅当∀x,y∈S,ax=ay⇔bx=by;
b.R*b当且仅当∀x,y∈S,xa=ya⇔xb=yb.
易知,L⊆L*,R⊆R*且
在半群S中,每个L*-类和每个R*-类至少含有一个幂等元,则称S是富足的;若富足半群S中的幂等元集E(S)形成半格,则称S是充足的,这时对有且∈E(S),使得若富足半群S的每个H*-类有且仅有一个幂等元,则称S是超富足的,这里H*=L*∧R*;若富足半群S的幂等元集形成子带,则称S是拟充足的.
设S是富足半群,它的幂等元集为E(S),T是S的富足子半群.若对T中所有的a,∃e∈T∩E(S),使得aL*e(aR*e),则称T为S的左(右)*-子半群.如果T既是左*-子半群,又是右*-子半群,那么,称T为S的*-子半群.
富足半群S的充足*-子半群S0称为充足断面,若对于,使得x=ex0f,其中,eL*x0+,fR*x0*(x0+,x0*∈E(S)).则满足条件的幂等元e,f是由x和eR*xL*f唯一确定[1].用ex表示e,用fx表示f,如果对∀x,y∈S,fxey∈E(S0),(fxey)0∈E(S0),则称充足断面S0为乘的(弱乘的).
由文献[2]可知,充足半群不一定是它自身的充足断面.假如充足半群T是它自身的充足断面,那么,T称为断面充足半群.
许多学者关注一个重要的广义正则半群类——富足半群类,并且也研究出带有不同充足断面的富足半群.
本文引进弱拟充足半群类,给出其基本概念,讨论其基本性质.同时证明出无零元且有乘充足断面的富足半群是弱拟充足的充分必要条件,以此来研究无零元且有乘充足断面的弱拟充足半群.
2 有充足断面的富足半群的性质
本文明确必要的记号,给出需要的结论.详见文献[1-5]
设S为富足半群,S0是S的一个充足断面,定义集合

显然,I和Λ的定义是对偶的.因此,对于I的任何结论,都有Λ的相应结论.现只讨论集合I.由文献[1-3,5]知引理1.
引理1 设S为有充足断面S0的富足半群,则

d.如果S0是乘的,有
(a)∀e∈E(S),有e0∈E(S0)且I是有乘逆断面E(S0)的左正规带;
(b)∀x,y∈S,有(xy)0=x0fxeyy0,exy=ex(xy)0+,fxy=(xy)0*fy;
(c)∀x,y∈S,有(xy)0=x0y0当且仅当S是拟充足;
(d)若S是正则的,那么,S0是S的乘逆断面;
(e)S满足正则条件;
(f)S同构于W,S0同构于T,W,T定义为
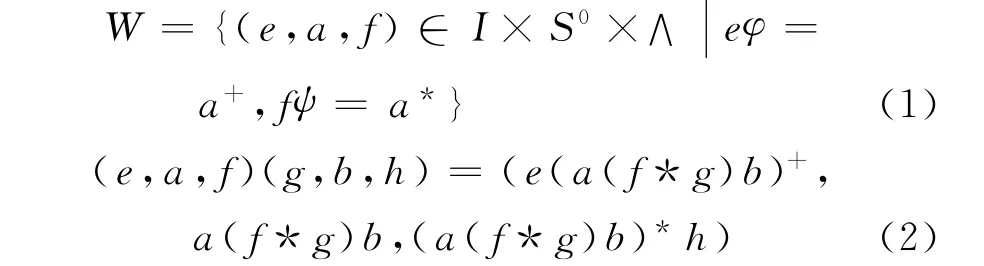
其中,x=a(f*g)b∈S0,T={(a+,a,a*)|∀a∈S0},定义映射φ,ψ,*

3 弱拟充足半群
由文献[6]知,半群同态映射φ:S→T称为*-同态映射,若对于

定义1 没有零元的富足半群S称为弱拟充足半群,如果存在断面充足半群T和一个满*-同态映射φ:S→T,使得对∀λ∈E(T),λφ-1是S的完全单子半群.
在上述定义中,若S是正则的,那么,S称为拟纯正的;如果T满足条件

那么,S称为自然富足半群;如果T是半格,那么,S称为完全富足半群.
如果S有零元,那么,定义1中的完全单概念则意味着完全0-单.
若S为拟充足(或拟纯正)半群,则由文献[7]中的命题1.7和1.8可知,存在自然*-同态映射:φ:S→T=S/σ,其中,T是断面充足半群,使得对λ∈E(T),Sλ=λφ-1是S的完全(0-)单子半群.由定义1可知,S是弱拟充足半群.这表明,弱拟充足半群概念是拟充足半群概念的推广.
现假设半群S是无零元且有充足断面S0的富足半群.
引理2 a.∀x,y∈S,有(x0y0)+=x0+y0+,(x0y0)*=x0*y0*.
b.如果S是弱拟充足的,那么,定义1中的φ是幂等可分的,即

证明 a.对x,y∈S,由引理1中的c得,(x0y0)+=(x0y0+)+.因为x0L*x0+,L*是S上的右同余,故x0y0+L*x0+y0+,x0+y0+∈E(S0).由L*-类幂等元的唯一性可知,(x0y0)+=(x0y0+)+=x0+y0+.
b.设e,f∈E(S),eφ=fφ.因φ是*-同态映射,故由eφL*fφ,eφR*fφ推得eL*f,eR*f.因为从而eLf,eRf并推得eHf,由H-类中若有幂等元,则唯一知,e=f.
引理3 若S0是乘的,那么,S是完全单半群当且仅当S0是群.
证明 假设S0是群,则由引理1的a和d知
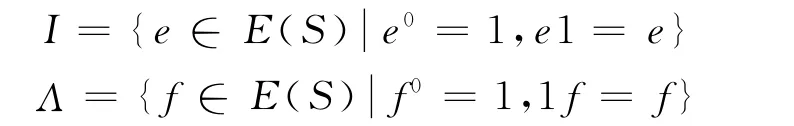
且W=I×S0×Λ.其中,1是群S0的单位元.若e,g∈I,有

故I是左零半群.同理,Λ是右零半群,W=I×S0×Λ的乘法运算为

由上可知,W 是S0上关于正则矩阵P=(f*g)Λ×I的Rees矩阵半群,即W=M(S0,I,Λ,P),因此,S是完全单半群.
反之,假设S是完全单半群,则知S是Rees矩阵半群M(G;I—,Λ—,P)[6],因S0是S的乘充足断面,由引理1中的d得S0是逆半群,它至少有一个幂等元.若(i,p,λ),(j,p,μ)∈E(S0),则它们均是(λ,pλi,i)的正则逆元.因S0是S的逆断面,所以,(i,p,λ)=(j,p,μ),即S0只有一个幂等元,因而S0是群.
引理4 若对x,y∈S,有(xy)0+=x0+y0+,(xy)0*=x0*y0*.令

则
a.μ是S上的同余;
b.μ∩(S0×S0)是S0上的幂等可分同余.
证明 a.显然,μ是等价关系.设(a,b)∈μ,c∈S,由条件等式知,a0+ea0*=b0+eb0*.于是,对e∈E(S0),有
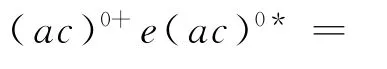
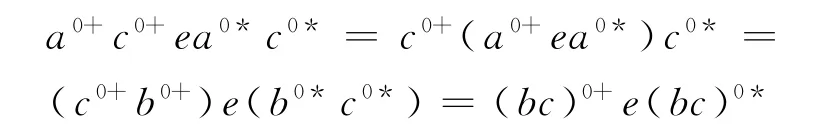
故(ac,bc)∈μ.同理,(ca,cb)∈μ,进而μ是S上的同余.
b.显然,μ∩(S0×S0)是S0上的同余.如果(e,f)∈μ∩(E(S0)×E(S0)),则e0+=e=e0*,f0+=f=f0*且对λ∈E(S0),eλe=eλ=fλf=fλ.特别取λ=e代入,有e=ee=fe,同样,取λ=f代入,有f=ff=ef.因为,E(S0)是半格,有ef=fe,故e=f.
半群S上的同余ρ称为充足半群同余,如果S/ρ是充足半群.
现证S为弱拟充足半群的充分必要条件.
定理1 设S0是乘的,则下列条件是等价的:
a.S是弱拟充足半群.
b.∀x,y∈S,有(xy)0+=(x0y0)+,(xy)0*=(x0y0)*.
c.引理4中的关系μ满足条件,
(a)μ是S0上的幂等可分同余;
(b)μ是S上的充足半群同余.
证明 a⇒b.假设S是弱拟充足半群,则存在断面充足半群T和满*-同态映射φ:S→T,使得对∀α∈E(T),αφ-1是S的完全单半群.对λ∈T,用Sλ表示λφ-1.设α∈E(T),x=exx0fx∈Sα,则xφ=(exx0fx)φ=(exφ)(x0φ)(fxφ).因φ是满*-同态映射,由xφ=α,exφ=eα=αα-1=α,fxφ=fα=αα-1=α,得

即x0φ∈V(α).
于是,x0φ=α-1=α且x0∈Sα,即对于∀α∈E(T),Sα都包含S0的一个幂等元.这表明Sα∩S0是Sα的乘充足断面.由引理3知,对∀α∈E(T),Sα是群.
如果λ∈T,exx0fx=x∈Sλ,因φ是满*-同态映射,故
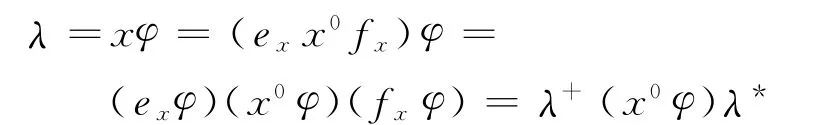

因λ=λλ*,t=t+t,且φ是满*-同态映射,故(xy)0∈Sλt,(xy)0+=e(xy)0∈Seλt=S(λt)+.另外,由(x0y0)φ=(x0φ)(y0φ)=λt知,x0y0∈Sλt.故
(x0y0)+=ex0y0∈Seλt=S(λt)+.因S(λt)+∩S0是群,故(xy)0+=(x0y0)+.由引理2中的a知,(xy)0+=x0+y0+成立.
同理,对∀x,y∈S,(xy)0*=(x0y0)*=x0*y0*成立.
b⇒c.假设对∀x,y∈S,(xy)0+=x0+y0+,(xy)0*=x0*y0*成立,由引理4知,μ是S上的同余,且μ∩(S0×S0)是S0上的幂等可分同余.可知S/μ是富足半群[5].于是,对x∈S,若f=x0+x0*∈E(S0),则有f0+=f+=f=f*=f0*,并对∀e∈E(S0),有f+ef+=x0+ex0*.于是,对∀x∈S,包含x的μ-类有一个幂等元f∈E(S0).如果xμ,yμ是S/μ的幂等元,则∃e,f∈E(S0),使得,事实上,xμ=eμ,yμ=fμ,e=x0+,f=y0+,于是

由此可知,S/μ是充足半群.即关系μ是S上的充足半群同余,因此,μ满足条件(a)和(b).
c⇒a.假设μ满足条件(a)和(b),对于∀x∈S,用Sx表示包含x的μ-类.显然,对于∀x∈S,x0∈Sx∩S0且Sx是富足的,故Sx∩S0是Sx的充足断面.又S0是S的乘充足断面,故Sx∩S0也是Sx的乘充足断面.由引理4知,Sx∩S0上有幂等可分同余μ∩((Sx∩S0)×(Sx∩S0)).所以,对∀xμ∈E(S/μ),Sx∩S0有且只有一个幂等元x0+x0*,因此,它是群.由引理3知,对∀xμ∈E(S/μ),Sx是完全单半群.于是,由定义1得,S是弱拟充足半群.
现说明弱拟充足半群类真包含拟充足半群类和拟纯正半群类作为子类,它也说明了有乘充足断面的弱拟充足半群的存在性.
例1 在文献[8]中,T=M0(G;I,Λ,P)是正则幂等生成半群,它带有零元,且含有一个乘半格断面T0={a,e},但T不是纯正的,它的Cayley表为

T中元的分解式


考虑T上的Rees矩阵半群S=M(T,I,Λ,P),其中,矩阵

S的乘法运算

通过计算,有:
a.S是有幂等元集E(S)的半群,其中

(e)=(e)iλ是零元(∀i∈I,λ∈Λ).因
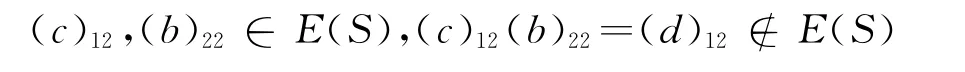
故E(S)不是带,且元(d)11,(d)12,(d)21不是正则的.因此,S既不是正则的,也不是拟充足的.
b.S是富足的.对∀(x)iλ,(y)jμ∈S,有

因此,S的L*-类和R*-类可表为
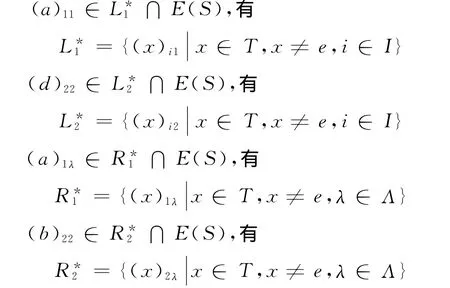
由上可知,S是富足的.
c.S是弱拟充足的.因对于(λ∈I,j∈Λ),有pλj=qλrj,存在S→T的映射φ

由(a)12φ=a,(b)11φ=b,(c)22φ=c,(d)21φ=d,(e)φ=e知,φ是S→T的满射.对(x)iλ,(y)jμ∈S,有

故φ是S→T的满同态映射.由式(5)知,(x)iλL*(y)⇔λ=μ,所以

当λ=1时,
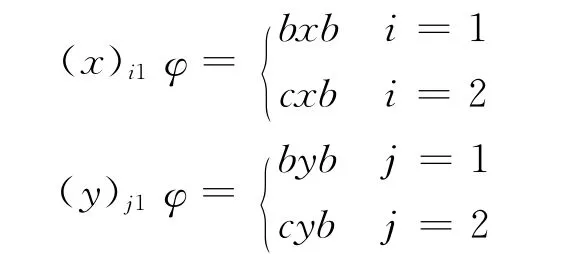
(b)11φ=b,故

即(x)i1φL*(y)j1φ⇔(x)i1L*(y)j1.剩余部分同样可经计算核准.因此,φ是满*-同态映射.若x∈E(T0)=T0,则Sx=xφ-1如下:

由前面可知,φ|S0是S0→T0的同构映射.现只需证明对S中的任何一个元都可以唯一地写成以下符合要求的形式.

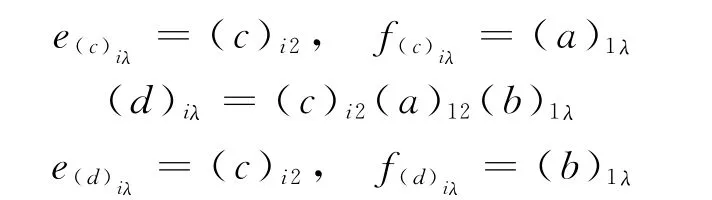
因此,对于(x)iλ,(y)jμ∈S,有f(x)iλe(y)jμ∈E(S0).
e.T是定义1意义下的拟纯正半群.
设ST={(e),(a)12,(b)11,(c)22,(d)21},显然,φ是ST→T的同构映射,ST是弱拟充足的(因对ST,Se={(e)},Sa={(a)12}),故T也是弱拟充足的.又T是正则的,所以,T是拟纯正的.
[1] El-Qallali A.On the construction of a class of abundant semigroup[J].Acta Math Hung,1990,56(1/2):77-91.
[2] 高振林,田丽.一种广义富足半群[J].上海理工大学学报,2011,33(2):198-204.
[3] El-Qallali A.Abundant semigroup with a multiplicatice type A transversal[J].Semigroup Forum,1993,47(1/2):327-340.
[4] El-Qallali A,Fountain J B.Quasi-adequate semigroups[J].Proc Roy Soc Edinburgh,1981,91(A):79-99.
[5] Guo Xiaojiang.Abundant Semigroups with a multiplicative adequate transversal[J].Acta Math Sinica(English Series),2002,18(2):229-244.
[6] Howie M.An Introduction to Semigroup Theory[M].London:Academic Press,1976.
[7] El-Qallali A.Quasi-Adequate semigroups[J].Semigroup Forum,1992,44(3/4):273-282.
[8] Blyth T S,McFadden R.Regular semigroups with multiplicative inverse transversals[J].Proc Roy Soc Edinburgh,1982,92(A):253-270.

