社会系统中舆情动力学的统计物理研究

郭 龙， 李 炜， 蔡 勖

（1.中国地质大学（武汉）数学与物理学院，武汉 430074；2.华中师范大学粒子物理研究所，武汉 430079；3.华中师范大学复杂科学中心，武汉430079）

人类社会是一个复杂的多组分系统，其最基本的组元不是粒子而是一个个具有思想的人，每一个个体都与其有限的同伴而不是系统中所有的个体发生相互作用，例如说服和被说服，合作出演一部电影等.由于人们不可能详细知道人类社会中每一个个体的基本运动方程.因此，对人类社会现象的基本原理探究和数学协同学运算就存在很大的挑战.尽管如此，人类社会还是具有极好的宏观性质.社会现象中无序向有序的转化，例如语言和文化的自发形成以及舆情一致态（即系统中所有个体都持有相同的舆情值）的涌现等.这些宏观性质要求统计物理方法和思想在社会中的应用.实现社会分析的量化，促使自然科学和人文科学的交叉融合.

自从17世纪“政治算术”和人口性别“误差曲线”的提出［1］，人们开始追寻用像物理学定理一样来描述社会现象，揭示社会现象背后的物理和社会规律.直到19世纪30年代，“社会物理学”才被首次提出，而将社会物理学分为“社会静力学”和“社会动力学”.人们试图从物质世界的量化到社会系统中的量化的类比研究中去解释“为什么人类行为如同粒子运动一样”，以及从微观角度的随机性和无序性来揭示社会宏观现象等一系列社会问题.

直到19世纪70年代，社会动力学才被物理学家广泛关注.社会物理学致力于用统计物理学方法和思想，对真实社会系统进行研究，寻找社会系统的拓扑特性，从而模拟分析宏观社会现象涌现的微观机制.人们从微观角度社会个体之间的相互作用的随机性和无序性来模拟研究大尺度的社会现象.例如舆情动力学形成和演化、社会网络上传播行为动力学、社会经济运行与安全的普适规律以及人类行为动力学.

从统计物理学角度来研究社会动力学时，一般需要知道如何描述系统中个体的行为.整个系统的宏观行为并不是这些个体的动力学行为的简单累积，而是依赖于系统中个体之间的相互作用，即社会系统的拓扑结构.然而社会系统中的个体不同于物理中基本粒子，他们是智能个体，他们的行为受到复杂的心理和生理过程的影响，不可能十分精确地了解个体的动力学行为，甚至包含个体之间的相互作用.因此，对社会现象的模拟描述不能面面俱到，否则，问题的极端复杂性将迫使人们束手无策.在对社会动力学系统模拟研究时就会碰到两个困难：一是模型构造的仿真程度，二是构造模型的微观行为所导致的宏观现象的涌现机制.

随着统计物理的发展，它为物理学家研究社会现象提供了可能.因为大尺度下社会现象一般不依赖于社会系统中个体的微观行为.另外，系统宏观呈现出来的对称性、标度率以及守恒律等是系统个体微观行为相互作用的结果.因此，在对社会系统的模型描述时，需要对某一社会现象的最简单的个体行为以及重要属性进行准确描述，进而研究社会系统中某一特殊现象的涌现行为.这就要求对社会系统的实证研究结果进行分析比对.

1 社会网络

社会网络是由个人或社会组织通过一定的相互作用关系而形成的一种网络［2－3］.在社会网络中，个人或社会组织称为网络的节点，而网络中的边体现在人与人之间或社会组织之间的相互作用关系.这种相互作用关系的方式是多样的，例如：人与人之间的朋友关系［4］，企业之间的商业来往关系［5］、家庭之间的联姻关系［6］、科学家之间的合作关系等［7－8］.

关于社会网络的量化研究可以追溯到20世纪20年代.关于社会网络的早期研究有：1926年Wellman研究了小学生朋友关系网［9］；1936年Davis及其合作者研究了南美妇女社交网络［10］；以及在20世纪30年代Mayo关于工厂工人社会关系网络的研究［11］.Rapoport是第一个用数学模型来模拟和研究社会网络的科学家，他首次在网络研究中引入了节点度分布的概念［10］.近年来，商业关系网络以及性关系网络的研究也得到了一定程度的关注.

一个关于社会网络的实验是著名的Milgram“小世界”实验［12－13］.在这个实验中，要求志愿者把信交给自己所认识的一个人，并且他认为通过这个人这封信可以经过尽可能少的传递次数最后转交到给定对象的手上.尽管大部分信件在传递过程中丢失，还是有四分之一的信件被传递到给定对象的手中.通过对这些成功传递的信件分析，这些信件从开始寄出到最后被传递到给定对象手中平均需要6个人的协助才能完成.这就是著名的“六度分离”的起源实验，尽管这个概念直到几十年后才被Guare提出来［14］.

社会网络的传统研究往往会碰到不精确、主观因素以及小样本等因素的影响.为了避免这些因素，许多研究者利用其它方法来研究社会网络.其中一个有丰富而又相对可靠的数据库的社会网络就是合作关系网.在这些合作关系网络中，合作的个体可以属于同一个团体也可以属于不同的团体，但是这些个体之间的合作关系却是同一种合作关系.例如电影合作网络中，演员可以具有不同的国籍，但是他们之间合作却是出演在同一部电影中.关于电影演员合作网络的数据库来自在线网络电影数据库（http：／／www.imdb.com／）.在电影演员合作网络中，节点就是出演电影的演员，而两个演员之间如果存在一条边表示这两个演员合作出演同一部电影.另一个著名的合作网络就是科学家合作网络.在科学家合作网络中，科学家表示节点，而如果表示科学家的节点之间存在一条边则表示这两个科学家合作完成一篇论文.Newman研究了4个科学家合作网络［7－8］，其中包括物理科学家合作网络、生物医学科学家合作网络、高能物理科学家合作网络以及计算机科学家合作网络.Barabási及其合作者研究了数学家合作网络和神经科学家合作网络［15］.

另一个具有可靠数据库的社会网络就是人们之间的个人交往网络.例如，可以构建一个社会网络，其中节点之间的连线表示人与人之间的邮件来往关系.Newman等对邮件网络进行了研究［16］.Barabási等通过分析个人邮件网络来分析研究人类行为动力学［17－22］.国内中科大汪秉宏小组研究了人类城市出行的回转半径［23］以及人类空间运动的层次性模型［24］.

大量实证分析表明：真实社会系统具有其特有的特性，例如小世界特性、节点度分布的无标度性和社团结构.一个显而易见的问题：这些拓扑特性的产生机制是什么，这些拓扑特性如何影响发生在社会网络中的动力学现象，例如疾病的传播、舆情的形成和演化等.本文将目光聚焦在社会网络的舆情动力学方向，对前人的工作进行简要的概述，以期能为初学者提供基本的参考和帮助.

2 舆情模型（opinion models）

达成协议是社会系统中最重要的活动之一［25］.在日常生活中会碰到各种各样的问题，这就需要与周围的小团体达成协议，例如观点、观念、行为甚至是意识形态等等，统称为舆情（opinion）.达成协议能促使其更强，进而增强其在社会中的地位和影响力［25］.社会系统中人们之间相互作用相互影响的复杂性决定了人们达成协议与否的动力学行为的复杂性.统计物理学家利用舆情动力学模型来定义社会系统中个体的舆情值以及个体之间的相互作用的基本过程.在数学模型中，舆情值往往是一个变量集，每一个个体的舆情值只能取变量集中的元素.变量集中的元素可以是离散的也可以是连续的.这样，面临的挑战就是如何构造足够的数学规则来描述系统中个体之间的相互影响和系统舆情值的演化.目前，较著名的舆情模型有：选举模型，Sznajd模型和Deffuant模型.

2.1 选举模型（voter model）

选举模型最早由Clifford和Sudbury在考虑物种竞争中提出来的.选举模型规则：首先，系统中每一个个体都赋予一个二进制变量s＝±1做为其舆情值；然后，每一演化步，个体i从它的邻居中选择一个邻居j并改变自己的舆情值而采用其所选邻居的舆情值sj.系统中个体舆情的效仿来自其邻居的压力.在选举模型中，个体只受到其所选择的一个邻居的影响而具有较大的涨落.早期，人们研究了规则格子上的选举模型，例如二维格子上演化成具有相同舆情值中心团增长而边缘蓬乱的斑图.

在规则格子上，选举模型可以精确地映射为随机行走模型，个体选择其一个邻居并采用其舆情值，犹如随机行走者被随机引导.因此，可以利用随机行走理论来研究选举模型.在d维格子中，每一个格点代表一个具体的个体.用集合S＝｛si｝表示系统的状态，其中si表示第i个格点的舆情值.然后，给出格点的舆情值发生反转的跃变概率Wk（S）＝W（sk→－sk）［26］，给出概率分布函数P（S）满足的主方程.从主方程中可知任意阶的关联函数都是收敛的，即它们不依赖于更高阶的函数.因此，关联函数是可解的［27］.许多学者分析研究了一阶关联函数和二阶关联函数，得到有意义的结果［27－28］.在完全图中，磁化强度几率分布的福克－普朗克方程具有与一维含位置依赖的扩散参数的扩散方程一样的形式［29］.因此，可以给出解析解.对于任意初始的磁化强度，有限系统达到一致相（即系统中所有节点拥有相同的舆情值）的平均时间可以精确计算，且与系统的大小N成比例.

实证研究表明，社会网络的节点度分布满足幂律分布，即网络中节点度的差异性很大，例如节点的活跃性、节点的影响力等，称之为网络节点的异质性（heterogeneous）.近年来，许多学者研究了网络的异质性对选举舆情演化的影响［30－34］以及小世界网络拓扑结构对选举模型演化的影响［35－36］.例如，Sood和Redner研究了无标度网络上的选举模型，发现系统达到一致相的平均时间TN与节点度分布指数γ满足N（2γ－4）／（γ－1）［30］.Yang等［37］提出了非线性选举模型，其中节点按照一定的概率采纳舆情值，其采用＋1的概率函数为p＋＝n＋a／（n＋a＋n－a），采用－1的概率为p－＝1－p＋，其中n＋a和n－a分别为节点及其邻居中持有＋1和－1的个数，α为可调参数.然后再规则格子和无标度网络上研究了非线性选举模型的达到一致相的时间与可调参数α之间的关系.

2.2 Sznajd模型

社会影响理论（social impact theory）是社会心理学中一个重要的理论.它描述了社会中个体如何受其同伴的影响以及它又如何影响其同伴.社会团体影响力的大小取决于社会团体中个体数量、个体或团体的说服力以及团体与被影响个体之间的距离.这一距离可以使空间距离表现为抽象空间中个体之间关系的亲疏性.Sznajd模型［38］就是基于这一原理提出来的.这里，以一维环为例阐述Sznajd模型的演化规则.由N个个体相连围成一维的环，每一个节点都与其左右邻居相连.si表示节点i的舆情值，且si是二进制变量±1表示节点i对某一事物的态度.每一时间演化步，随机选择两个相邻的节点作为说服者，例如节点i和节点（i＋1）.他们将根据其舆情值来说服其邻居（i－1）和（i＋2）改变他们的舆情值，其说服规则为

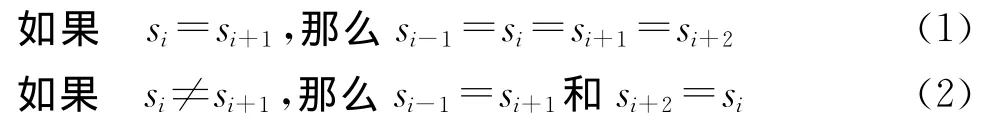
其中，规则（1）是铁磁规则，规则（2）是反铁磁规则.因此，如果说服者具有相同的舆情值，他们将成功说服其邻居采用与之相同的舆情值；反之，两个说服者分别说服对方的邻居采用与之相同的舆情值，从而瓦解对方.这就是所谓的“和则成，离则败”（united we stand，divided we fall）.

许多学者模拟研究了不同网络拓扑结构上的Sznajd模型，以及改进Sznajd模型演化动力学［29，39－50］.研究了小世界网络上的Sznajd模型，发现长程连接具有增强系统创成关联的作用，从而促使系统演化到一致相［51］.一些学者利用统计物理方法对Sznajd模型进行理论分析.Slanina等研究了完全图中类Sznajd模型的精确解［30］.Sznajd等给出了Sznajd模型演化动力学的合理的哈密顿形式［52－54］.

Sznajd模型被广泛应用到不同领域，可用来描述政治竞选行为［43，46］.被选举者的支持者分布满足幂律关系P（n）～1／n，其中P（n）表示被选举者有n个支持者的概率.它也可用描述个人倾向之间的相互作用与经济活动之间的关系，以及开放市场中不同产品之间的竞争行为［55］和不同团体之间的舆情传播行为［56］.

2.3 Deffuant模型

前文提到的选举模型和Sznajd模型是特殊的离散舆情动力学模型.然而，在某些情况下，人们对某一事物的舆情值是可以从一个极端向另一个极端连续变化的［25］.例如，一个人对某一事物的关注程度，例如教育，它不仅仅局限于“非此即彼”而是可以处于这两者之间的某一取向.在日常生活中，人们之间的依据其舆情值的不同区分出亲疏关系.并不是任何人之间都可以信息交流，人们对与其交流有一定的信任范围，称之为有限信任（bounded confidence）原理.在模型中，用一个实数ε来表示有限信任原理，称之为信任参数.两人之间的舆情值差异如果小于ε，他们将协商各自做出让步向着对方舆情值的方向改变自己的舆情值.反之，什么也不做.其中，Deffuant模型就是一个典型的连续舆情模型［57］.

考虑含有N个个体的群体.用含有N个节点的网络来描述这个群体，其中节点表示群体中的个体，而节点之间的边表示这两个节点将会相互彼此影响.起始，每一个节点i都随机地从［0，1］中选择一个数作为此节点的舆情值si.每一演化步，随机地选择一个节点和这个节点的一个邻居.假设在t时刻选中了一对邻居节点i和节点j，它们的舆情值分别为si（t）和sj（t）.Deffuant模型的演化规则为：如果｜si（t）－sj（t）｜＞ε节点i和j什么也不做；如果｜si（t）－sj（t）｜＜ε，他们将协商各自做出让步，向着对方舆情值的方向改变自己的舆情值，即

其中，μ∈［0，0.5］为收敛参数，它反应了两节点的舆情值各自向对方舆情值的方向改变的大小.如果μ＝0.5，两节点协商后采用的舆情值相同且等于他们商谈前舆情值的平均值，即si（t＋1）＝sj（t＋1）＝si（t）＋sj（t）／2.因此，Deffuant模型的演化基于妥协原理.无论ε和μ取何值，系统的平均舆情值都为1／2，其在Deffuant模型中是不变的.

Deffuant模型的演化依赖于舆情空间边界处的不稳定性.舆情传播的不稳定性将促使系统中节点的舆情值之差拉大，从而形成具有不同舆情值的子团体.一旦不同团体之间的舆情值的差距就会被拉开从而大于ε.最后，系统演化成一系列的δ函数.通常而言，子团体中节点的数目与信任参数有关，而μ影响系统演化的收敛时间.然而，当μ很小时，子团体构型也会受到μ的影响［58］.在完全图、规则图、随机图和无标度网络中，当ε＞εc＝0.5，系统中所有的节点拥有一样的舆情值s＝0.5.称之为一致相［59－60］，与网络结构无关.当ε＜εc时，系统中出现多个具有明显舆情值差异的子团体，其中每个子团体中的节点具有相同的舆情值.

蒙特卡洛模拟显示系统最终演化成不同子团体的数目nc近似满足表达式1／2ε［25］.不同子团体的节点之间的舆情值相差至少一个信任参数，他们之间不能发生相互作用.因此，在相差两个信任参数的子团体中间不会存在另一个子团体，所以比率1／2ε可以准确地确定nc.关于Deffuant模型的大部分结果都是通过模拟得到的.然而，在特殊情况下，一些学者理论分析了Deffuant模型演化动力学，例如，Ben－Naim利用几率方程描述了完全图中的Deffuant模型动力学［61］.

受到Deffuant模型的启发，大量学者研究了改进的Deffuant模型.这些模型都各有侧重地研究了社会系统中某些现象和特性.Lorenz等考虑了个体信任参数ε的差异性［62－66］；Ben－Naim考虑了系统中个体对其opinion的自发改变［67］；Carletti及其合作者考虑了外在周期扰动对个体的影响［68］；以及我们考虑了个体收敛参数μ的差异性［69］.

3 总结与讨论

以上扼要介绍了3种著名的舆情演化动力学模型，以及前人在规则格子和复杂网络上开展的一些工作，旨在期望能为初学者提供一定的参考和帮助.对社会系统上舆情动力学的研究目前仍主要处于模拟研究阶段，其理论分析仍面临着巨大的挑战.第一，在理论物理中，系统遵循的基本原理是最小作用量原理，那么在社会系统中人类行为遵循什么样的基本原理，羊群效应还是个人收益最大还是其它，以往模型中往往只能考虑其中一个对社会舆情动力学的影响，比如多数模型（Majority－rule model）考虑的是羊群效应.寻找人类社会系统中遵循的基本原理仍是一个重要的研究方向，如研究人类行为动力学，国内的中国科技大学和上海理工大学在这方面做了大量的研究工作.第二，在互联网发达的今天，舆情演化似乎可以摆脱地域的限制，但是人类活动的局域频繁性和全局随机性将导致真实空间网络中舆情传播的研究的必要性.第三，媒体网络化和互联网的发展对舆情演化产生了重要的影响，例如药家鑫事件，媒体的这种外在属性在社会系统的舆情演化中扮演怎样的角色.第四，社会系统网络是一个耗散系统和多样性系统，其拓扑结构又是如何与舆情动力学相互耦合进行演化的.这些问题的探讨有助于进一步理解社会复杂系统，为舆情的防控提供一定的理论依据.

［1］ 范泽孟，刘怡君，汪云林，等.社会物理学国际前沿研究透视［M］.付允译.北京：科学出版社，2007.

［2］ Wasserman S，Faust K.Social network analysis：methods and applications［M］.Cambridge：Cambridge University Press，1994.

［3］ Scott J.Social network analysis：a handbook［M］.London：SAGE Publications，2000.

［4］ Moody J.Race，school integration，and friendship segregation in America［J］.Amer J Sociol，2001，107（3）：679－716.

［5］ Mariolis P.Interlocking directorates and control of corporations：the theory of bank control［J］.Social Sci Quart，1975，56：425－439.

［6］ Padgett J F.Ansell C K.Robust action and the rise of the medici［J］.Amer J Sociol，1993，98（6）：1259－1319.

［7］ Newman M E J.Scientific collaboration networks I network construction and fundamental results［J］.Phys Rev E，2001，64（1）：016131.

［8］ Newman M E J.Scientific collaboration networksⅡshortest paths，weighted networks，and centrality［J］.Phys Rev E，2001，64（1）：016132.

［9］ Boccaletti S，Latora V，Moreno Y，et al.Complex networks：structure and dynamics［J］.Phys Rep，2006，424（4／5）：175－308.

［10］ Newman M E J.The structure and function of complex networks［J］.SIAM Rev，2003，45（2）：167－256.

［11］ Scott J.Social network analysis：a handbook［M］.London：SAGE Publications.2000.

［12］ Milgram S.The small－world problem［J］.Psych Todat，1967，1（1）：60－67.

［13］ Travers J，Milgram S.An experimental study of small world problem［J］.Sociometry，1969，32（4）：425－443.

［14］ Guare J.Six degrees of separation：aplay［M］.New York：Vintage，1990.

［15］ Barabási A L，Jeong H，Néda Z，et al.Evolution of the social network of scientific collaborations［J］.Physica A，2002，311（3／4）：590－614.

［16］ Newman M E J，Forrest S，Balthrop J.Email networks and the spread of computer Viruses［J］.Phys Rev E，2002，66（3）：035101（R）.

［17］ Vázquez A，Oliveira J G，DezsöZ，et al.Modeling bursts and heavy tails in human dynamics［J］.Phys Rev E，2006，73（3）：036127.

［18］ Barabási A L.The origin of bursts and heavy tails in human dynamics［J］.Nature，2005，435（7039）：207－211.

［19］ Vázquez A，Rácz B，Lukács A，et al.Impact of nonpoissonian activity patterns on spreading processes［J］.Phys Rev Lett，2007，98（15）：158702.

［20］ Vázquez A.Exact results for the Barabási model of human dynamics［J］.Phys Rev Lett，2005，95（24）：248701.

［21］ DezsöZ，Almaas E，Lukács A，et al.Dynamics of information access on the web［J］.Phys Rev E，2006，73（6）：066132.

［22］ Oliveira J G，Barabási A L.Human dynamics：Darwin and Einstein correspondence patterns［J］.Nature，2005，437（7063）：1251.

［23］ Yan X Y，Han X P，Zhou T，et al.Exact solution of gyration radius of individual’s trajectory for a simplified human regular mobility model［J］.Chin Phys Lett，2011，28（12）：120506.

［24］ Han X P.Hao Q，Wang B H，et al.Origin of the scaling law in human mobility：hierarchy of traffic systems［J］.Phys Rev E，2011，83（3）：036117.

［25］ Castellano C，Fortunato S，Loreto V.Statistical physics of social dynamics［J］.Rev Mod Phys，2009，81（2）：591－646.

［26］ Frachebourg L，Krapivsky P L.Exact results for kinetics of catalytic reactions［J］.Phys Rev E，1996，53（4）：3009－3012.

［27］ Scheucher M，Spohn H.A soluble kinetic model for spinodal decomposition［J］.J Stat Phys，1988，53（1／2）：279－294.

［28］ Evans J W，Ray T R.Kinetics of the monomermonomer surface reaction model［J］.Phys Rev E，1993，47（2）：1018－1025.

［29］ Slanina F，Laviccka H.Analytical results for the Sznajd model of opinion formation［J］.Eur Phys J B，2003，35（2）：279－288.

［30］ Sood V，Redner S.Voter model on heterogeneous graphs［J］.Phys Rev Lett，2005，94（17）：178701.

［31］ Sood V，Antal T，Redner S.Voter models on heterogeneous networks［J］.Phys Rev E，2008，77（4）：041121.

［32］ Castellano C，Loreto V，Barrat A，et al.Comparison of voter and Glauber ordering dynamics on networks［J］.Phys Rev E，2005，71（6）：066107.

［33］ Sychecki K，Eguíluz V M，Miguel M S.Conservation laws for the voter model in complex networks［J］.Europhys Lett，2005，69（2）：228－234.

［34］ Baxter G J，Blythe R A，Mckane A J.Fixation and consensus times on a network：a unified approach［J］.Phys Rev Lett，2008，101（25）：258701.

［35］ Castellano C，Vilone D，Vespignani A.Incomplete ordering of the voter model on small－world networks［J］.Europhys Lett，2003，63（1）：153－158.

［36］ Vilone D，Castellano C.Solution of voter model dynamics on annealed small－world networks［J］.Phys Rev E，2004，69（1）：016109.

［37］ Yang H X，Wang W X，Lai Y C，et al.Convergence to global consensus in opinion dynamics under a nonlinear voter model［J］.Phys Lett A，2012，376（4）：282－285.

［38］ Sznajd－Weron K，Sznajd J，Opinion evolution in closed community［J］.Int J Mod Phys C，2000，11（6）：1157－1165.

［39］ Stauffer D，Sousa A O，Oliveira S M.Generalization to square lattice of Sznajd sociophysics model［J］.Int J Mod Phys C，2000，11（6）：1239－1245.

［40］ Chang I.Sznajd sociophysics model on a triangular lattice：ferro and antiferromagnetic opinions［J］.Int J Mod Phys C，2001，12（10）：1509－1512.

［41］ Rodrigues F A，Costa L D F.Surviving opinions in Sznajd models on complex networks［J］.Int J Mod Phys C，2005，16（11）：1785－1792.

［42］ Elgazzar A S.Applications of small－world networks to some socio－economic systems［J］.Physica A，2003，324（1／2）：402－407.

［43］ González M C，Sousa A O，Hermann H J.Opinion formation on a deterministic pseudo－fractal network［J］.Int J Mod Phys C，2004，15（1）：45－57.

［44］ He M，Li B，Luo L.Sznajd model with“social temperature”and defender on small－world networks［J］.Int J Mod Phys C，2004，15（7）：997－1003.

［45］ Bartolozzi M，Leinweber D B，Thomas A W.Stochastic opinion formation in scale－free networks［J］.Phys Rev E，2005，72（4）：046113.

［46］ Bernardes A T，Stauffer D，Kertész J.Election results and the Sznajd model on Barabási network［J］.Eur Phys J B，2002，25（1）：123－127.

［47］ Bonnekoh J.Monte carlo simulations of the ising and the Sznajd model on growing Barabási－albert networks［J］.Int J Mod Phys C，2003，14（9）：1231－1235.

［48］ Sousa A O.Consensus formation on a triad scale－free network［J］.Physica A，2005，348：701－710.

［49］ Sousa A O，Sánchez J R.Outward－inward information flux in an opinion formation model on different topologies［J］.Physica A.2006，361（1）：319－328.

［50］ González－Avella J C，Eguíluz V M，Cosenza M G，et al.Local versus global interactions in nonequilibrium transitions：a model of social dynamics［J］.Phys Rev E，2006，73（4）：046119.

［51］ Guo L，Cai X，The key role of shortcuts of smallworld network in opinion formation［J］.Int J Mod Phys C，2008，19（6）：867－873.

［52］ Sznajd－Weron K.Controlling simple dynamics by a disagreement function［J］.Phys Rev E，2002，66（4）：046131.

［53］ Sznajd－Weron K.Dynamical model of Ising spins［J］.Phys Rev E，2004，70（3）：037104.

［54］ Sznajd－Weron K.Mean－field results for the two component model［J］.Phys Rev E，2005，71（4）：046110.

［55］ Sznajd－Weron K，Weron R.How effective is advertising in duopoly markets［J］.Physica A，2003，324（1／2）：437－444.

［56］ Sznajd－Weron K，Weron R.A simple model of price Formation［J］.Int J Mod Phys C，2002，13（1）：115－123.

［57］ Deffuant G，Neau D，Amblard F，et al.Mixing beliefs among interacting agents［J］.Adv Complex Systems，2000，3（1／2／3／4）：87－98.

［58］ Porfiri M，Bollt E M，Stilwell D J.Decline of minorities in stubborn societies［J］.Eur Phys J B，2007，57（4）：481－486.

［59］ Fortunato S.Universality of the threshold for complete consensus for the opinion dynamics of Deffuant et al［J］.Int J Mod Phys C，2004，15（9）：1301－1307.

［60］ Lorenz J，Urbig D.About the power to enforce and prevent consensus by manipulating communication rules［J］.Adv Complex System，2007，10（2）：251－269.

［61］ Ben－Naim E，Krapivsky P L，Rednes R.Bifurcations and patterns in compromise processes［J］.Physica D，2003，183（3／4）：190－204.

［62］ Lorenz J.Heterogeneous bounds of confidence：meet，discuss and find consensus［J］.Complexity，2010，15（4）：43－52

［63］ Deffuant G，Amblard F，Weisbuch G，et al.How can extremism prevail？a study based on the relative agreement interaction model［J］.J Artif Soc Soc Simul，2002，5（4）：1－2.

［64］ Deffuant G，Amblard F，Weisbuch G.Modelling group opinion shift to extreme：the smooth bounded confidence model［C］∥Proceedings of the European Social Simulation Association Conference.Valladolid：2004.

［65］ Deffuant G.Comparing extremism propagation patterns in continuous opinion models［J］.J Artif Soc Soc Simul，2006，9（3）：8－9.

［66］ Aldashev G，Carletti T.Benefits of diversity，communication costs，and public opinion dynamics［J］.Complexity，2009，15（2）：54－63

［67］ Ben－Naim E，Redner S.Dynamics of social diversity［J］.J Stat Mech：Theory Exp，2005，2005（11）：L11002.

［68］ Carletti T，Fanelli D，Grolli S，et al.How to make an efficient propaganda［J］.Europhys Lett，2006，74（2）：222－228.

［69］ Guo L，Cai X.Continuous opinion dynamics in complex networks［J］.Commun Comput Phys，2009，5（5）：1045－1053.