一类具有变人口规模的含时滞SIS流行病模型的全局稳定性

翟院青， 原三领， 袁艳燕

（上海理工大学理学院，上海 200093）

文献［1］讨论了具有变人口规模含积分时滞的SIS流行病模型

式中，I（t）、N（t）分别为t时刻的染病者和总人口.模型中所有参数均为正常数：A为人口的常数迁入，并假设迁入的均为易感者；β为传播系数；d、ε分别为人口的自然死亡率和因病死亡率.P（t）为染病者患病t单位时间后仍为染病者的比例.在模型（1）中，若假设每个染病者个体的染病期为常数，则模型（1）将成为一个与之等价的微分差分方程.在文献［1］中，确定了疾病传播的基本再生数，得到了无病平衡点全局渐近稳定以及地方病平衡点局部渐近稳定的条件.此类含时滞流行病模型的地方病平衡点全局稳定性的证明对从事流行病建模和研究的工作者来说历来是一件非常棘手的事情，现有的工作大多局限于通过构造Liapunov函数的方法来证明［2－8］.本文将在文献［1］的基础上进一步探讨疾病传播的持续性以及地方病平衡点全局渐近稳定的条件.

1 模 型

假设每个染病个体的染病期为一常数ω，即P（t）为一分段函数

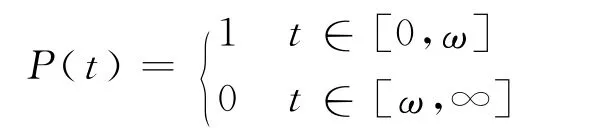
则模型（1）成为与之等价的微分差分方程

定义

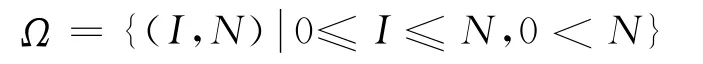
由文献［1］知，疾病的基本再生数为

且模型（2）有下面的结论：

引理1 对于模型（2）从Ω中出发的解，下面结论成立：

a.如果I0（0）＝0，则对所有的t≥0有I（t）≡0，N（t）→A／d（t→∞）；

b.如果N（0）≥I0（0）＞0，则对所有的t＞0有N（t）＞I（t）＞0.

引理2 模型（2）总存在无病平衡点（0，A／d）.如果R0≤1，则模型没有其它平衡点；如果R0＞1，则模型还存在一个地方病平衡点

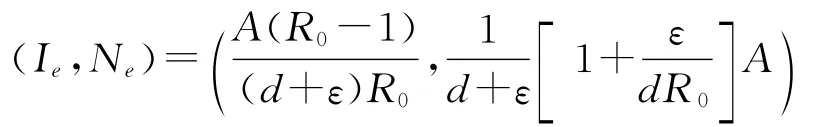
引理3 如果R0＜1，无病平衡点（0，A／d）在区域Ω内全局渐近稳定；如果R0＞1，无病平衡点（0，A／d）在区域Ω内不稳定.

引理4 a.如果R0≥2＋ε／d或1＜R0≤3，则地方平衡点（Ie，Ne）局部渐近稳定；b.如果ε／d≤1，则对于所有的R0＞1，地方平衡点（Ie，Ne）局部渐近稳定.

2 流行病的持续性

令I1＝M2－M1／R0，且假设I1＞0.取η满足0＜η≤I1，则有

设（I（t），N（t））为模型（2）初值满足I0（0）＞0的解，则有下面的结论：

引理5 如果I1＞0，对于任意的t0＞0，不可能对所有的t＞t0有I（t）＜I1－η.

证明 假设引理5的结论不成立，则存在t0＞0与t1（t1＞t0＋ω），对于t≥t1－ω，有

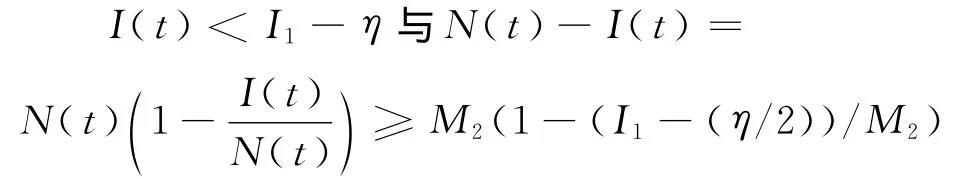
将其代入积分方程（与模型（2）中第一个方程等价），得

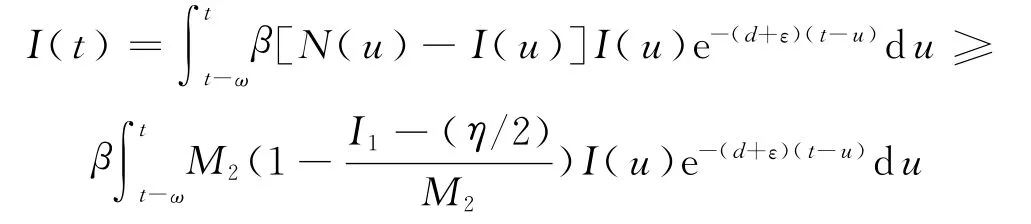
令Ie＝mint∈［t1，t1＋ω］I（t），则对所有的t≥t1，有I（t）≥Ie.否则，存在t2（≥t1＋ω），使得I（t2）＝Ie且对所有的t1≤t≤t2有I（t）≥I（t2）.故

取常数R1满足，则对于任意的t≥t1＋ω有I（t）＞IeR1.注意到Iee－（d＋ε）（t1＋ω－u）du≥IeR1.如果上述结论不成立，则存在t3≥t1＋ω，使得I（t3）＝IeR1且对所有的t1＋ω≤t≤t3有I（t）≥IeR1.另一方面在区间［t1＋ω，t3］上，有

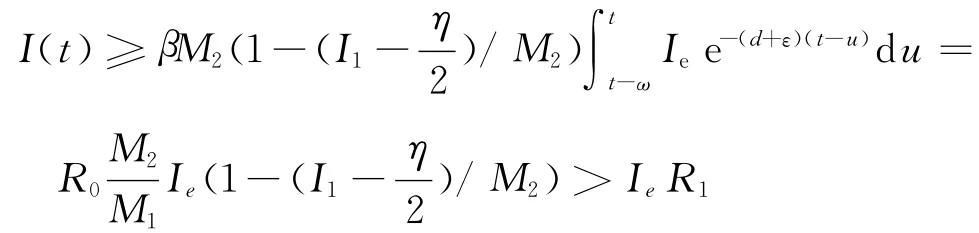
与I（t3）＝IeR1矛盾，故上面结论成立.由归纳法知在区间［t1＋kω，∞）上有I（t）＞IeR.所以当t充分大时有I（t）≥I1－η，这与I（t）＜I1－η（t≥t1）矛盾.故引理5得证.

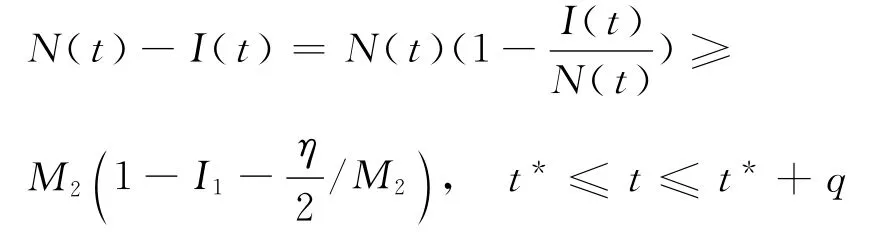
因为模型（2）的解一致有界，故I（t）一致连续，所以存在τ（0＜τ＜ω）（τ与t＊无关），使得（t＊≤t≤t＊＋τ）.如果q≤τ，结论自然成立.下面考虑τ＜q≤ω的情况.对于t＊＋τ≤t≤t＊＋q，有

3 地方平衡点的全局渐进稳定性

首先，对传染者人数的最终下界给出估计.令

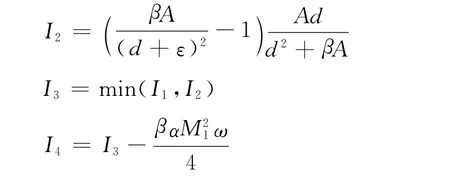
证明 首先，假设I3＝I1.由引理5，对于所有充分大的t不可能都有I（t）＜I3－η.如果I（t）≥I3－η（t充分大），结论显然成立.如果I（t）在I3－η左右震荡（t充分大时），则存在足够大的t4、t5，使得

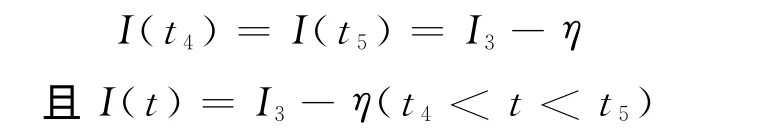
下面考虑t4－t5≥ω的情况.如果（t），由引理5的证明过程，可知

首先对Il的值进行估计.为此，考虑与模型（2）等价的模型

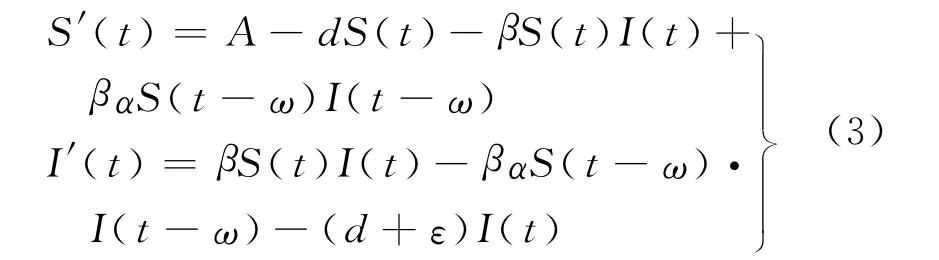
其中，S（t）为t时刻易感者的人数，满足N（t）＝S（t）＋I（t），这里α＝exp（－（d＋ε）ω），因为

对于t4＜t＜t4＋ω，据I（t）＜I3＜I2，可得I′（t）≥－因此，有

故Il≥I4－η.即证当I3＝I1时，命题成立.同理可证I3＝I2时，结论也成立，引理6得证.

下面分析模型（2）地方平衡点的全局稳定性.在下文中总假设模型（3）存在唯一的地方平衡点为（Se，Ie），其中

模型（3）可以写成为

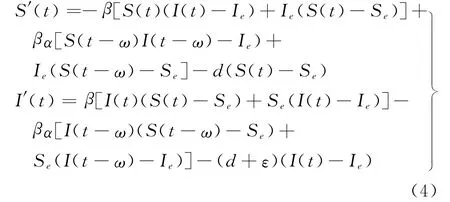
令V1＝S－Se－Seln（S／Se）＋I－Ie－Ieln（I／Ie）.

则V1沿着模型（4）解的全导数为

再令V＝V1＋V2，其中

计算V沿着模型（4）解的全导数，得

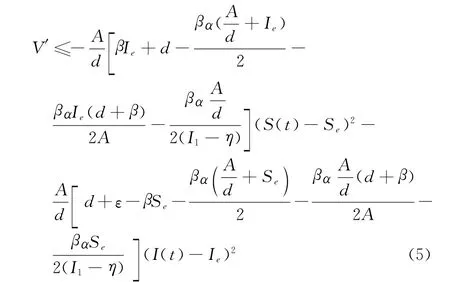
如果m＞0且n＞0，在η＞0足够小的情况下，式（5）关于变量（S－Se），（I－Ie）定负.下面定理2是本文的主要结论.

定理2 如果以下条件成立：

则模型（3）的地方病平衡点全局渐近稳定.

注：易见当α足够小且d＋ε＞βSe时，定理2的条件显然满足.

5 结 论

在文献［1］所研究的SIS流行病模型的基础上对疾病流行的持续性以及地方病平衡点全局稳定性做了进一步探讨.研究结果表明：当R0≥1＋（ε／d）时，疾病会持续流行，从而形成地方病.通过构造恰当的Liapunov泛函，得到了地方病平衡点是全局渐近稳定的一个充分条件.对于所有的R0≥1地方病平衡点也许都是全局渐近稳定的，这有待下一步继续研究.

［1］ 袁艳燕，原三领，翟院青.一类具有变人口规模的含时滞SIS流行病模型的稳定性分析［J］.上海理工大学学报，2012，34（1）：27－31.

［2］ Wang W，Ma Z.Global dynamics of an epidemic model with time delay［J］.Nonlinear Analysis：Real Word Application，2002，3（3）：365－373.

［3］ Wang W.Global behavior of an SEIRS epidemic model with time delays［J］.Applied Mathematics Letters，2002，4（15）：423－428.

［4］ Hethcote H W，Driessche P V.Two SIS epidemiologic models with delays［J］.J Math Biol，2000，40（1）：3－26.

［5］ Yuan S，Han L，Ma Z.Analysis of an SIS epidemiologic model with variable population size and a delay［J］.Appl Math J Chinese Univ Ser B，2003，18（1）：9－16.

［6］ Yuan S，Ma Z.Study on an SIS epidemiologic model with time variant delay［J］.System Science and Complexity，2002，15（3）：299－306.

［7］ 原三领，马知恩，韩茂安.一类含时滞的SIS流行病模型的全局稳定性［J］.数学物理学报，2005，25（3）：349－356.

［8］ Yuan S，Ma Z.Global stability and Hopf bifurcation of an SIS epidemic model with time delays［J］.System Science and Complexity，2001，14（3）：327－336.