基于粗糙集和BP神经网络的飞航导弹备件消耗规律预测

徐廷学，杜爱国，陈 红

（1．海军航空工程学院兵器科学与技术系，山东 烟台 264001；2．海军装备部，北京 100048）

飞航导弹备件需求预测方法很多，如时间序列预测法、回归预测法与专家系统法等[1]。时间序列预测法不能充分利用对备件需求量有很大影响的信息和因素，可能导致预测不准确和数据稳定性差；回归预测法不能处理影响因素与需求量间的非平衡暂态关系；专家系统法在把专家知识和经验等准确地转化为一系列规则时非常困难。进行飞航导弹备件消耗规律的研究，必须立足于深入研究飞航导弹备件消耗的影响因素之上[2]。全面掌握各种影响因素及其性质，可使本文的研究工作获得有力支撑。现实情况是，飞航导弹备件种类繁多，而影响其消耗的因素种类多、影响程度各异，导致在数据处理上耗费大量精力。如果某些影响因素对预测结果造成的影响微小，那么就可以通过忽略这些因素来降低预测的难度，提高预测的速度和有效性。本文提出基于粗糙集和BP 神经网络的预测法。该方法充分发挥粗糙集在处理冗余数据上的优势，结合BP神经网络对飞航导弹备件进行消耗预测，提高了预测的速度和有效性。

1 粗糙集与BP 神经网络的基本原理

1.1 粗糙集基本原理

粗糙集理论是波兰华沙大学的pawlak2 教授于1952年提出的一种处理模糊性和不确定性新型数学工具。该理论能有效地处理不精确、不一致和不完整信息，并从中发现隐含知识，揭示潜在规律。目前，该理论已被广泛应用于数据挖掘、机器学习、知识获取、决策分析、人工智能、大型数据库和智能信息处理等计算机领域。

如果给定一个有限的非空集合U，称为论域，R 为U 上的一族等价关系，则知识可以定义为等价关系族R 对论域U 的划分，记为U/R。假设根据关于论域U 的某种信息，使用属性及其值来描述U 中的元素，属性或属性集合就构成了U 上的一族等价关系。任意一个等价关系r R∈ 可以对U 划分，形成等价类，称为关于r 的基本集。如果2 个元素同属于一个等价类，则它们之间是不可分辨的。

粗糙集理论中，模糊性是一种基于边界的概念，即一个模糊概念具有一个没有明确界限的边界，每个不精确的概念X 由一对精确概念(下近似与上近似)来表示。X 的下近似包含了可确切分类到X 中的元素，上近似包含了所有那些可能属于X 的元素。上近似与下近似的差就是概念的边界区域，即利用可用信息不能确定地分类到概念中的所有元素。显然，如果边界区域非空，则X 是一个模糊概念。

1.2 BP 神经网络基本原理

神经网络是在现代神经科学的基础上提出和发展起来的，旨在反映人脑结构及功能的一种抽象数学模型[3-4]。自1943年美国心理学家W.McCulloch和数学家W.Pitts 提出形式神经元的抽象数学模型—MP 模型以来，人工神经网络理论技术已经过了50 多年曲折的发展，特别是20 世纪80年代，人工神经网络的研究取得了重大进展[5]。

误差反向传播网络(Back Propagation Network，BP)是一种应用最广泛的神经网络。BP 模型是一个多层感知器，是由输入层、中间层(隐含层)和输出层构成的前馈网络。BP 神经网络自学习过程是一个反复迭代过程，首先给网络一组初始权值，然后输入一个样本并计算其输出，通过实际输出与期望值之间差值用一定方法来修改网络权值，以达到减小这个差值的目的。反复执行这个过程直到这个差值小于预先确定的值为止。对足够的样本进行这样的训练后，网络所得的那组权值便是网络经过自适应学习得到的正确内部关系。[6]

H.N.Robert(1989)证明了对任意闭合区间连续函数都可以用含有一个隐含层的BP 网络来逼近，因而BP 网络可以来预测器材的消耗量[7-9]。

2 粗糙集和BP 神经网络预测模型的建立

利用粗糙集处理影响因素的值，以影响因素作为输入，并以消耗量作为输出，建立基于粗糙集和BP 神经网络的预测模型，其预测流程如图1 所示。

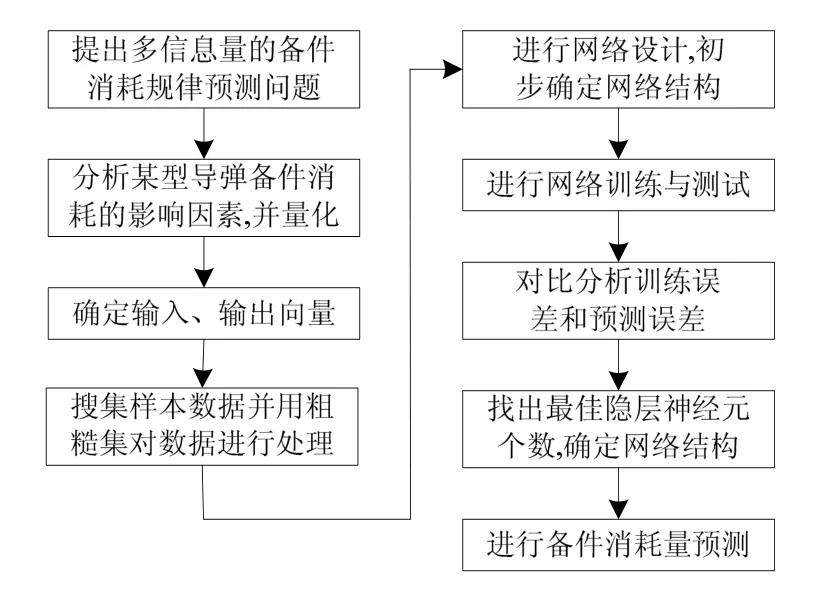
图1 基于粗糙集和神经网络的预测流程

Step1：提出多信息量的备件预测问题，构思建立基于粗糙集和神经网络的预测模型；

Step2：分析并量化影响备件消耗量的各因素。影响备件消耗量的因素很多，如备件的固有故障率、重大演习任务、环境因素、使用维修与定检等。根据具体情况把各影响因素量化，并用适当的数字表示出来；

Step3：确定输入输出向量，把影响因素量化值作为输入向量，把备件消耗量作为输出向量；

Step4：收集数据并用粗糙集理论对数据进行处理；

Step5：确定输入与输出层神经元个数，并设计中间层神经元个数可变的网络结构；

Step6：输入训练样本与测式样本进行网络训练与测试，对比训练误差和预测误差，确定最优网络结构；

Step7：输入新的影响因素样本数据到确定的最优模型中进行预测。

3 应用分析

参照某飞航导弹8年备件的消耗，消耗量统计数据及主要影响因素编制见表1。应用基于粗糙集和神经网络预测法进行飞航导弹备件消耗量分析。

表1 影响因素量化值

3.1 分析主要影响因素并量化

1)各影响因素如下：

A——备件的固有可靠性。把导弹装备定检过程中发现的失效备件数作为自然消耗的备件数并对其量化。

B——环境因素。根据该部队气象部门的统计资料，将其量化为根据环境的严酷度所划分的7 个等级，并相应地量化为7～1 之间的整数值，即数值越大表示严酷程度越高，环境越恶劣。

C——人为因素。以导弹技术准备过程中因人为因素导致的备件失效数为该影响因素的量化值。

D——年度重大演习任务次数。将次数作为量化值。

E——执行任务时间。根据平时训练计划统计出该导弹年度使用总时间，单位为h，将其作为量化值。

F——年度使用、维修与定检中该备件(或者含该备件的部件)被拆卸的总次数。将总次数作为量化值。

3.2 运用粗糙集方法对数据进行约简处理

各影响因素组成属性集合R={A,B,C,D,E,F}。

年度组成集合U={1,2,3,4,5,6,7,8}。

对每个属性设定阈值，1 表示不小于阈值，0表示没有达到标准。例如，对A，阈值设定为2，当A 值没有达到2 时，阈值为0，否则阈值为1；对B，阈值设定为3；对C，阈值设定为3；对D，阈值设定为1；对E，阈值设定为650；对F，阈值设定为27。表2 为影响因素信息表。

表2 影响因素信息表

由表2 可知D 属性值在8年跨度里只有一个不同，这说明每年重大演习次数对备件的影响程度基本稳定，对预测不会有太大影响，可以把它去掉。B 属性值和F 属性值相同，所以只保留一个，假设保留B，删除F。这样删除表2 中D、F 两列，得到影响因素化简信息表，见表3。

表3 影响因素化简信息表

下面对表中的数据进行约简。 其中，U={1,2,3,4,5,6,7,8}，R={A,B,C,E}。则A、B、C 和E 分别具有以下等价类：

ind(R)关系有以下等价类：

因此，因素B 可省，而A、C 和E 不可省。这样就把原来6 个影响因素减为3 个。

3.3 运用神经网络进行消耗量预测

采用3 层BP 神经网络，输入层有3 个神经元，输出层有1 个神经元。把选定的消耗特征参数A、C 和E 作为神经网络的输入向量，备件的消耗量作为神经网络的输出向量。

中间层的神经元个数需要通过实验来确定，因而需要设计一个隐含层可变的BP 网络。一般可先根据Kolmogorov 定理取2n+1 个，再依据经验在附近选择不同的个数进行实验寻找最佳数目。依实际情况分别选取6、10、15、20、25、29、33 和40进行实验。按BP 网络的一般设计原则，中间层神经元的传递函数为S 型正切函数tansig，输出层神经元的传递函数可设定为S 型对数函数logsig。中间层神经元个数很难确定，但在很大程度上影响着网络的预测性能[4]。

取表1 的影响因素数据作为输入向量，以紧跟后8年的消耗数量作为目标向量进行网络训练。训练次数设为1 000，训练目标设为0.000 1，其他参数取默认值。依照上面设计网络，观察不同个数隐单元构成的BP 网络训练曲线，分别检查网络性能，一般收敛速度较快且能够达到训练精度的网络为优。

以此类推，取某年影响因素数据作为测试样本，得到各网络输出值后，分别再与下年实际消耗量相比较，将此误差也作为选择最优网络结构重要依据之一。一般取收敛速度最快且误差最小网络结构为最优网络结构。

在最优网络模型中输入某年的影响因素数据，从而可以预测次年的备件消耗量。

利用MATLAB 语言[10-11]编制描述该BP 网络预测模型的计算机程序。运行该程序，可得到不同隐单元数的网络训练误差曲线图如图2 所示。

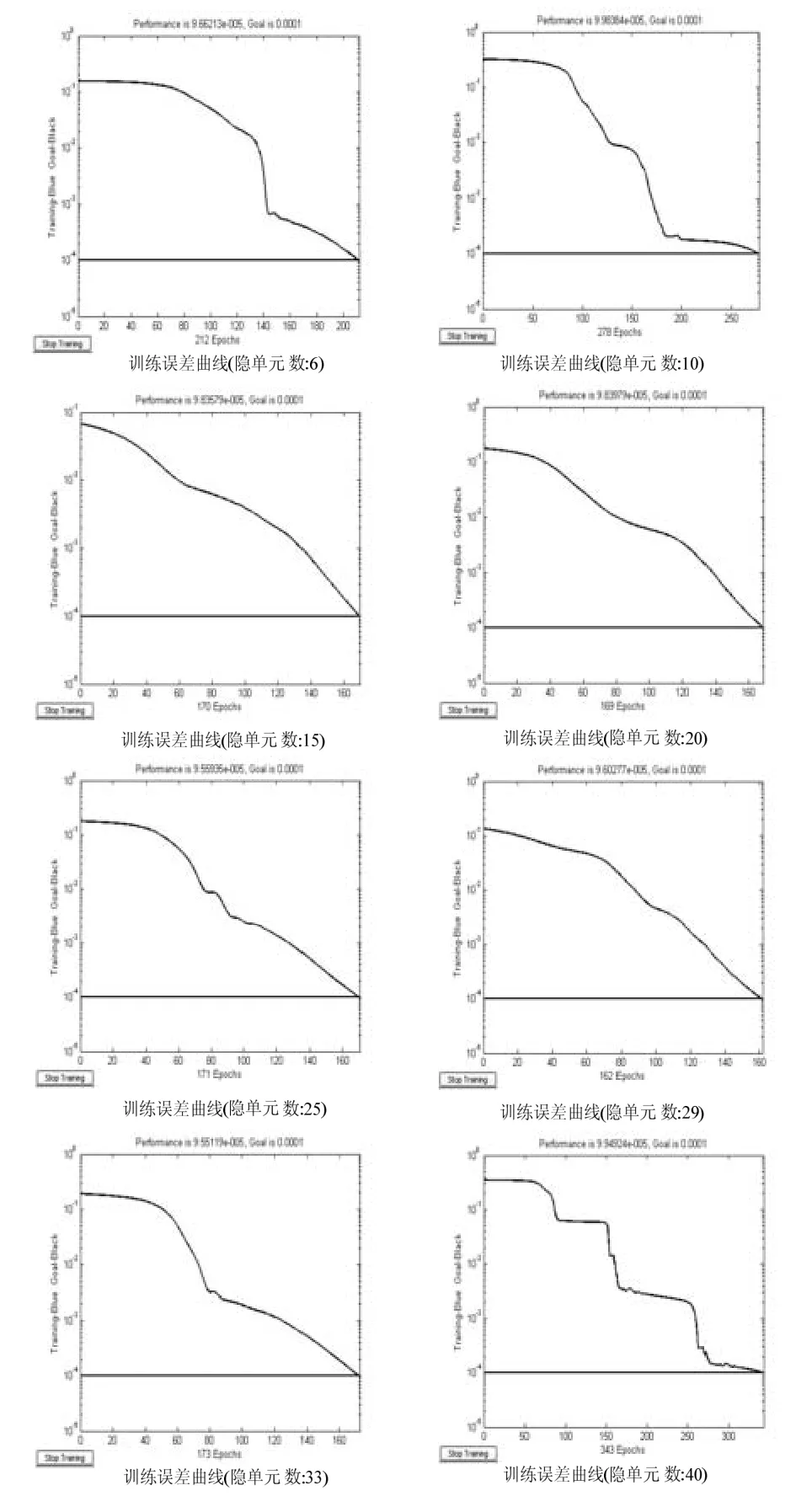
图2 不同隐单元数的网络训练误差曲线对比图

从图2 中看出，训练次数与预测误差不随隐单元数增加而线性增加或者减少，也证明了隐单元数增加可以提高网络映射精度，但并不意味着一定提高网络性能的重要结论。当隐单元数为29 时，网络只需训练162 次就能达到精度要求，可以作为最优网络模型。

在最优网络模型中输入某年的影响因素数据，预测次年的备件消耗量时。网络的训练误差曲线见图3。若其预测输出为0.876 5，反归一化并取整数得年该备件的消耗量为30 个。

可以看出，经过粗糙集对影响因素数据约简化处理，在神经网络中输入的数据量虽然大为减少，但预测结果还是比较贴近实际值，并没有出现预测值与实际值之间相对误差变的太大的问题，这就说明了所提出的基于粗糙集与BP 神经网络的预测方法在进行飞航导弹备件消耗预测时的预测数据可信度高，预测方法好用。

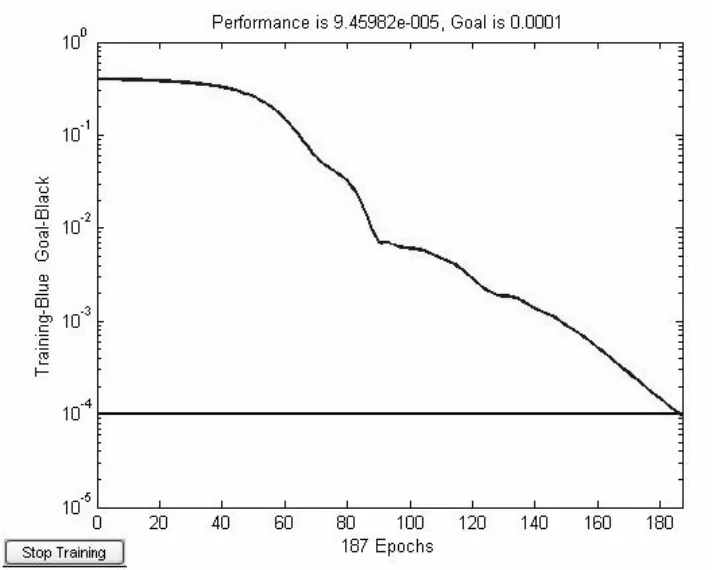
图3 实际预测网络的训练误差曲线

4 结束语

本文提出基于粗糙集和BP 神经网络的飞航导弹备件消耗规律预测方法，该方法能发挥粗糙集在处理冗余数据上的优势。结合BP 神经网络对飞航导弹备件进行消耗预测，大大提高了预测的速度和有效性。通过应用分析表明，该方法能达到很好的预测效果。

[1] 牟讴红. 某型机备件需求确定过程和方法的研究[D]. 北京∶ 北京航空航天大学, 2000∶4-7.

[2] 徐廷学. 装备综合保障工程理论与方法[M]. 北京∶ 兵器工业出版社, 2009∶4-5.

[3] 沈世镒. 神经网络系统理论及其应用[M]. 北京∶ 科学出版社, 1998∶56-59.

[4] 葛哲学, 孙志强. 神经网络理论与MATLAB R2007实现[M]. 北京∶ 电子工业出版社, 2007∶23-58.

[5] 岳付昌, 阎群章, 徐廷学, 赵明. 神经网络在装备使用阶段质量评估中的应用[J]. 四川兵工学报, 2010, 31(11)∶56-59.

[6] 高隽. 人工神经网络原理及仿真实例[M]. 2 版. 北京∶机械工业出版社, 2007∶43-54.

[7] 金伟. BP 神经网络在维修保障系统能力评估中的应用[J]. 计算机仿真, 2005,22(10)∶43-46.

[8] 顾钧元, 徐廷学, 陈海建, 等. 基于BP 神经网络的产品寿命分布类型选择[J]. 电子产品可靠性与环境试验, 2011,29(1)∶42-45.

[9] 黄天辰, 韩京才, 叶术青, 等. 基于神经网络的弹药消耗预测[J]. 军械工程学院学报, 2004,16(2)∶29-31.

[10] 景振毅, 张泽兵, 董霖. MATLAB 7.0 实用宝典[M]. 北京∶ 中国铁道出版社, 2008∶23-205.

[11] 董长虹. MATLAB 神经网络与应用[M]. 北京∶ 航空工业出版社, 2005∶64-80.