使用电场传感器阵列的水下运动目标检测与参数估计

包中华，龚沈光，马 珂

（1．海军航空工程学院电子信息工程系，山东 烟台 264001； 2．海军工程大学兵器工程系，武汉 430033；3．海军驻上海地区电子设备军事代表室，上海 200233）

航行于海水中的船舶，无论是电化学作用引起的腐蚀电流，还是为了防腐人为外加的阴极保护电流，都会在海水中产生电场[1]。船舶电场是船舶目标在水下的一种基本物理场，难以人为消除或隐身；尤其是其准静态电场成分，集中了船舶电场大部分能量，并且在海水中传输损耗小，是水下电场探测系统的可靠信号源[2-3]。国外各主要海洋国家，长期以来十分重视水下目标电场探测理论和应用的研究，取得了很多成果，部分成果已转化为实际装备。

由于船舶电场的水下场分布特征具有变化的复杂性，因而利用电场进行水下目标检测和参数估计也是完全可能的。目前，国内外学者在电场研究中普遍使用水平电偶极子来建模水下船舶电场[4]。文献[5]使用单个电场矢量传感器提取水下目标航行参数，其问题主要是探测距离较近，参数估计精度较差。文献[6]通过在垂直海面方向布置2 个电场矢量传感器，可反演估计出偶极子源的水平位置，但该方法受测量噪声影响较大，而且作用距离有限。本文使用电场矢量传感器组成水平线列阵，提取水下运动目标准静态电场的空时特征，研究了基于电场传感器阵列的水下运动目标检测与参数估计问题。仿真结果表明，该方法具有良好的效果。

1 运动船舶水下电场分布模型

目前国内外使用的水下目标电场模型主要是水平分层模型[7-9]。在海水较深时，可以不考虑海底对电场分布的影响，使用空气—海水2 层模型；在浅水时，使用空气—海水—海底3 层模型以考虑海底的影响；在海水电导率随水深变化复杂时，使用水平n层模型。

建立平面直角坐标系Oxyz，其中平面0=z为海平面，区域z＞0 为空气。在空气—海水2 层模型下，区域0＜z为海水；在空气—海水—海底3 层模型下，−D＜z＜ 0区域为海水，z＜−D区域为海底，其中D为海深。目标和传感器阵列均在海水中，其中目标在海水中的深度为h(h≥ 0)，方向为x轴正向，且假设目标沿着x轴正向作匀速直线运动，速率为v。传感器阵列固定于海水中某区域。但是，由于目标的运动，故在目标坐标系中的坐标随时间变化，记为(xm(n),ym(n),zm)。假设了目标只在水平面内运动，而zm与时间无关。

在2 层模型条件下，n时刻在第m个阵元处，目标准静态电场3 个分量为：

在3 层模型条件下，n时刻在第m个阵元处，目标准静态电场3 个分量为：

式(4)～(6)中：

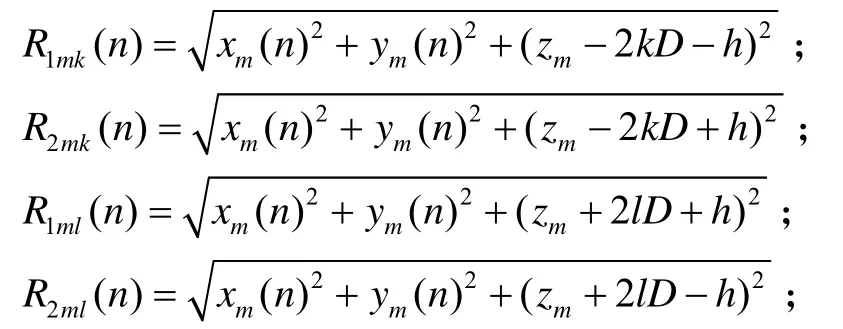
η=σ2为海底电导率；其他参数同上。

2 基于阵列的目标检测与参数估计

2.1 问题描述

假设传感器阵列由M个阵元组成，第m个阵元在n时刻接收到的观测信号为xm(n)，其中：m=0,1,2, … ,M−1，n=0,1,2, … ,N−1。记n时刻目标在第m个阵元处产生的电场强度值为sm(n)，此时该传感器的观测噪声为wm(n) 。每次检测都使用N个快拍的数据，将这些数据按照列转出方式进行排列，得到一个MN维列矢量：

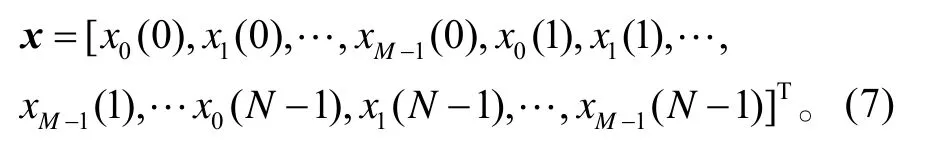
同理，也将信号和噪声数据表示成与式(7)相同的矢量形式，分别记为s和w。

考虑到在远场条件下目标电场的垂直分量要明显地小于其水平分量。因此，使用水平线列阵对目标进行检测和参数估计，如图1 所示。假设传感器阵列由M个阵元组成，阵元间距为d，阵列首阵元在目标坐标系中的初始水平坐标为 (x0,y0)，未知参数有x0、y0、v、h和φ，则坐标xm(n),ym(n),zm可用这些参数表示为：

式(8)中，φ表示水平线列阵基线方向与目标坐标系x轴正向的夹角。

图1 电场传感器阵列布放示意图

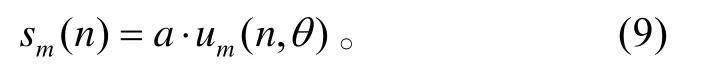
式(9)中：um(n,θ)为n时刻单位强度水平直流电偶极子在第m个阵元处的场分量，称为模型计算值。

2.2 方法原理

目标检测面临的背景噪声w由电场传感器自噪声和海洋环境电场噪声2 部分组成，其中传感器自噪声在去除直流分量之后，可认为其无论在时域上还是在空域上都是不相关的；而海洋环境电场噪声在时域上满足不相关的假设，在传感器阵列各阵元相隔较远的条件下，在空域上也可假设其是不相关的。因此，得到如下的假设检验问题：

式(10)中：噪声w为高斯白噪声，均值为0，方差为2σ=CI。由此，可以得到零假设和备择假设下包含未知参数θ的似然函数分别为：

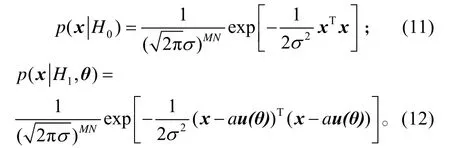
式(12)中，u(θ)为um(n,θ)的列转出排列矢量。

如果

则LGRT 判1H成立。

将式(11)、(12)代入式(13)中，并取对数和化简，可以得到

将式(14)右边不包含数据的项放入门限中并化简，可得到如下GLRT 检测器：

式(15)所示的GLRT 检测器是数据x的线性函数，因此TG(x)也近似服从高斯分布。采用N-P 准则，设定虚警概率为PFA，不难得到检测门限为[10]

同理，该GLRT 检测器的检测概率为

2.3 求解算法

式(16)所示是一个典型的非线性无约束寻优问题。求解此类问题，一种可行的方法是网格搜索法，通过在离散的参数空间上进行逐点搜索，寻找到全局极值点。这种方法的优点是算法必然会收敛到全局极大值点，缺点是计算量巨大。为了提高求解速度，必须使用迭代算法，考虑到目标函数十分复杂，所以较为适宜的是使用随机搜索算法。虽然常用的随机搜索算法都只能收敛到局部最优解，但实践表明，通过多次的设置初始点，随机搜索算法也能近似收敛到全局最优解。在随机搜索算法收敛后，还可以在收敛点的一个较小的邻域内使用网格法进行二次精确搜索，以提高参数估计的精度和检测算法的性能。

3 仿真试验

仅考虑背景噪声为高斯白噪声的情况，使用式(15)所示的GLRT 检测器和式(16)所示的最大似然估计器。假设目标的初始位置在(0,0, 20 m)−处，以速度v=10 m/s 沿x轴正向作匀速直线运动，目标的等效电偶极距为p=100 Am ，传感器每隔2 s 进行一次采样，使用的随机搜索算法为Hooke-Jeeve 方法，不进行二次精确搜索。

分别研究2 层模型和3 层模型下的目标检测与参数估计问题。

仿真试验1：海洋环境为深海，使用2 层模型进行计算。相关的仿真条件为：水平线列阵布于海面以下5 m 处，阵列首阵元在目标坐标系中的水平位置为(800 m,600 m)，阵元间距20 md=，阵元数为8，阵列基线与x轴正向夹角φ=120°，即参数估计问题的真值为θ=[800,600,10,20,120°]T。噪声由计算机仿真产生，分别设定信噪比为−10 dB、−3 dB、0 dB、3 dB 和10 dB 进行仿真试验，每种信噪比条件下均进行20 次随机试验，统计并计算这20 次仿真试验参数估计结果的均值和标准差，见表1、表2。

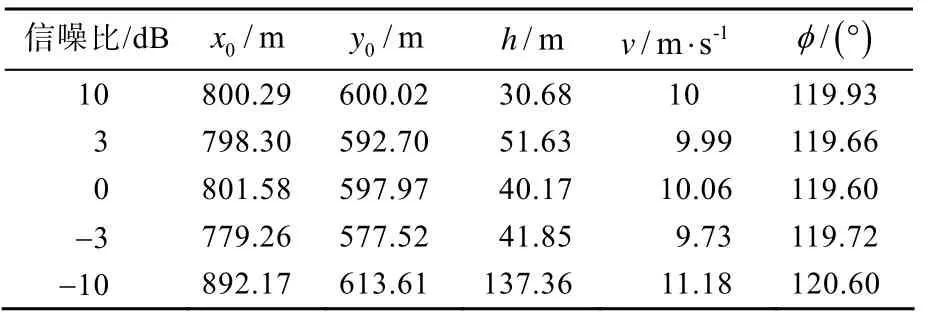
表1 2 层模型下参数估计均值

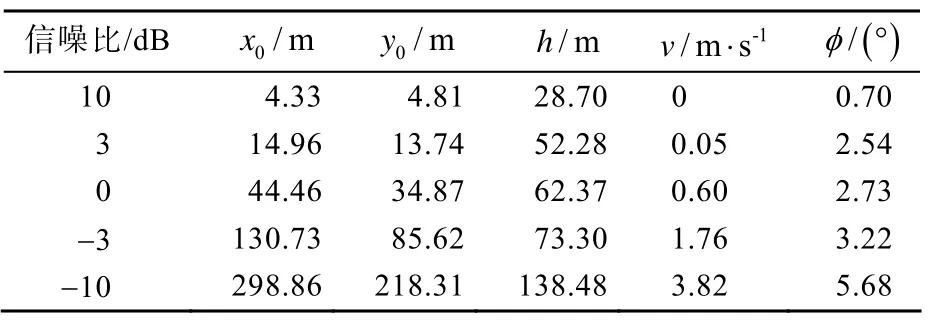
表2 2 层模型下参数估计标准差

仿真试验 2：海洋环境为浅海，海水深度D=60 m ，使用3 层模型进行计算。各种仿真条件和参数与仿真试验1 相同。3 层模型下仿真试验结果示于表3 和表4。

表3 3 层模型下参数估计均值

表4 3 层模型下参数估计标准差

观察表1～4 所示的参数估计结果，可以发现：

1)本文方法在背景噪声为高斯白噪声和目标做匀速直线运动的条件下，当信噪比大于0 dB 时，能够保证较好的估计精度；

2)无论是深海还是浅海条件下，水平线列阵都不能对目标在海水中的深度进行估计，这是由于水平线列阵的固有缺陷造成的；

3)水平线列阵对目标运动方向φ的估计精度较高，且对信噪比下降较为不敏感，即使在信噪比低至−10 dB 的条件下，估计标准差也不大于9°；

4)使用Hooke-Jeeve 方法进行随机搜索求解速度较快，在使用装有Intel Celeron 1.8 GHz CPU 芯片和1 G 内存的PC 机的条件下，2 层模型和3 层模型下的平均耗时分别为6.35 s 和145.94 s；若使用二次精确搜索，还可进一步提高估计精度。

分别将表1～4 所示的参数估计结果的均值及其正负3 倍标准差代入式(15)所示的GLRT 检测器，可得到−10 dB 时的目标检测结果，示于图2 和图3，为了便于对比，图中也分别给出了该信噪比条件下匹配滤波器的理论ROC 曲线。

由图2、3 可知，仿真检测结果与理论分析结果较吻合，在信噪比低至−10 dB 时，虽然在参数估计的过程中，除了φ以外都有着较大的误差，但是检测器TG(x)仍有着良好性能，其平均性能接近匹配滤波器，并且在3 层模型下检测更稳健。

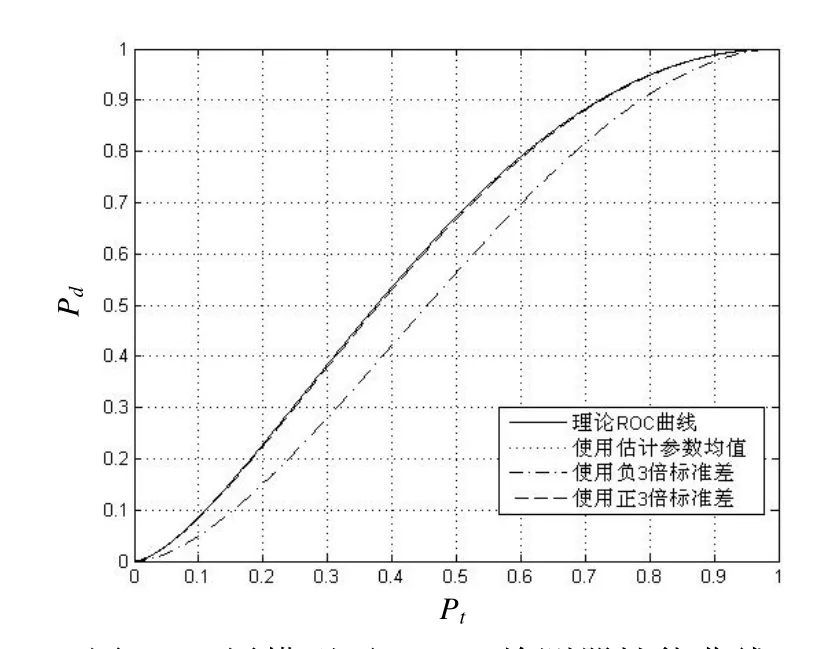
图2 2 层模型下GLRT 检测器性能曲线

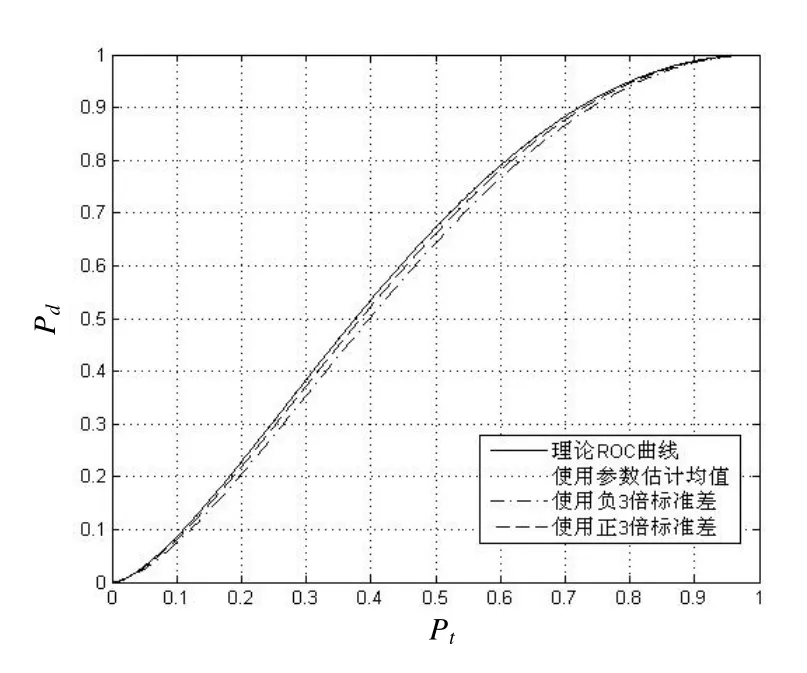
图3 3 层模型下GLRT 检测器ROC 曲线

4 结束语

本文使用水平直流电偶极子描述运动船舶水下准静态电场特征，在此基础上，使用电场传感器阵列提取该电场的空时分布特征，运用最大似然比方法，初步实现了对水下准静态电场目标的检测与参数估计。仿真试验结果表明，该方法在信噪比高于10 dB 时对除深度外的目标运动各参数均有着良好的估计性能，在信噪比高于−10 dB 时对目标运动方向仍能较精确地估计，此时进行目标检测，GLRT检测器有着接近匹配滤波器性能。下一步研究的重点是如何建立更为精确的船舶水下准静态电场模型以及提高模型计算的速度。

[1] 林春生, 龚沈光. 舰船物理场[M]. 北京∶ 兵器工业出版社, 2007∶239-240.

[2] 龚沈光, 卢新城. 舰船电场特性初步分析[J]. 海军工程大学学报, 2008,20(2)∶1-4.

[3] DYMARKOWSKI K, UCZCIWEK J. Ship’s electric field detection[C]. Paris∶ UDT Europe, 2002∶12C-3.

[4] 吴重庆, 赵爽. 电偶极子源定位问题研究[J]. 物理学报, 2007,56(9)∶5180-5184.

[5] DONATI R, CADRE J P LE. Detection of oceanic electric fields based on the generalized likelihood ratio test[C]//IEEE. Proceeding of Radar, Sonar Navigation. 2002,149(5)∶221-230.

[6] 包中华, 龚沈光, 孙剑英, 等. 使用双矢量传感器定位深海中的水平直流电偶极子源[J]. 海军工程大学学报, 2011,23(3)∶53-57.

[7] 陈聪, 李定国, 龚沈光. 基于拉氏方程的舰船静态电场深度换算[J]. 电子学报, 2010,38(9)∶2025-2029.

[8] 倪海, 孙明, 龚沈光. 半无限大海水空间中水平直流电流元产生的电磁场计算[J]. 装甲兵工程学院学报, 2006,20(1)∶1-4.

[9] 陈聪, 龚沈光, 李定国. 浅海中静态电偶极子电场分布的镜像法研究[J]. 武汉理工大学学报∶ 交通科学与工程版, 2010,34(4)∶716-720.

[10] KAY S M. 统计信号处理基础—— 估计与检测理论[M]. 北京∶ 电子工业出版社, 2006∶610-619.